基于柔性動力學仿真的齒輪拓撲優化

蘇成龍 羅肇藝 糜沛紋 秦國鋒 曹蘭

廣西師范大學 廣西桂林市 541004

1 前言

齒輪在傳動系統中屬非常重要的部件，傳動較為平穩，傳動比精確且效率較高；隨著工業制造的進步，齒輪的性能研究也逐漸增加，對設計出性能良好、強度較高且質量輕的齒輪有著較高的要求；齒輪的拓撲優化設計是目前最常用的優化方法，通過改變結構布局，獲得較佳的性能與體積質量。

目前，姚廷強等人對剛性與柔性的齒輪進行動力學建模分析，得出柔性齒輪更符合實際傳動的結論。高海龍等人基于多體動力學對柔性體齒輪副進行仿真，在動力學仿真過程中考慮了柔性體的自身變形對系統的影響。薛云偉對齒輪進行輕量化設計、動力學分析與拓撲優化等，達到滿足強度與輕量化的要求。蘭州研究齒輪等傳動系統等設計的理論和方法，提出了采用齒輪參數多目標優化和齒輪幅板結構拓撲優化兩步減重的設計方法。

2 建立齒輪模型

使用UG 軟件建立嚙合齒輪，模數為2.5，齒寬為16mm，主動齒輪為17 齒，從動齒輪為47齒，傳動比為2.76；嚙合齒輪如圖1所示。

圖1 嚙合齒輪

3 齒輪柔性化

使用Hypermesh 軟件將齒輪轉換為柔性體，生成MNF 中性文件，所選擇的材料為45 號鋼，45 號鋼的力學性能如表1 所示；

表1 力學性能

4 齒輪動力學仿真

動力學仿真得出一定負載和一定工況下的碰撞嚙合力、轉矩以及角速度的數據；本文對嚙合齒輪的仿真分析采用剛性對剛性、剛性對柔性、柔性對柔性的三種耦合仿真，選取最接近理論值的耦合仿真方案。

4.1 理論計算

4.1.1 碰撞參數計算

上式中，K 為剛度系數，n 為接觸指數，x為接觸距離，d為穿透深度，c為阻尼函數，當接觸距離x 小于接觸函數的距離變量x時，產生接觸力；當接觸距離x 大于接觸函數的距離變量x時，接觸力為零。

接觸剛度的表達式為

在設置接觸中，力指數取1.5，阻尼取5×10N·s/m，穿透深度取1×10m，靜摩擦因數取0.1，動摩擦因數取0.06，靜平移速度取0.1m/s,摩擦平移速度取1.0m/s。

4.1.2 嚙合力理論計算

其中，T 為輸入的轉矩，r 為從動輪的半徑，α 為壓力角，故將設置的數值T=100N/m，r=0.05875m，α=20°代入公式中，計算得碰撞嚙合力的理論值為F=1810.77N。

4.1.3 轉矩理論計算

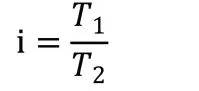
4.1.4 誤差值

4.2 齒輪動力學仿真

將嚙合齒輪導入Adams View 中，設置重力為9.80665N，單位制選擇MKS，積分求解器選擇WSTIFF，積分格式選擇SI2，添加驅動與接觸，輸入轉矩為100N/m，設置階躍函數，STEP（time,0,0d,0.1,1000d），仿真終止時間設為0.5 秒，步數設為1000 步。

4.2.1 嚙合齒輪剛性耦合

齒輪仿真分析，如圖2 所示；查看轉矩情況，齒輪在嚙合過程中，曲線圖變化較大且不規律，轉矩最大值為229.26N/m，平均值為42.21N/m，如圖3 所示。

圖2 齒輪剛性耦合仿真

圖3 齒輪轉矩曲線圖

對數據結果進行分析，如表2 所示。

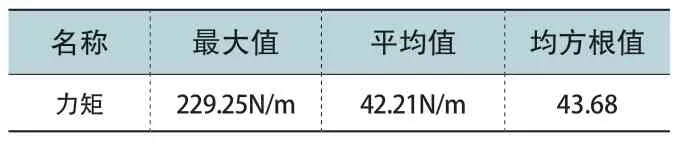
表2

4.2.2 嚙合齒輪剛柔耦合仿真

剛柔耦合齒輪仿真分析，如圖4 所示。查看轉矩情況，轉矩曲線趨于平緩，運動呈規律性，在0-0.5 秒的傳動中，轉矩最大值為69.38N/m，平均值為39.41N/m 如圖5 所示。

圖4 齒輪剛柔耦合仿真

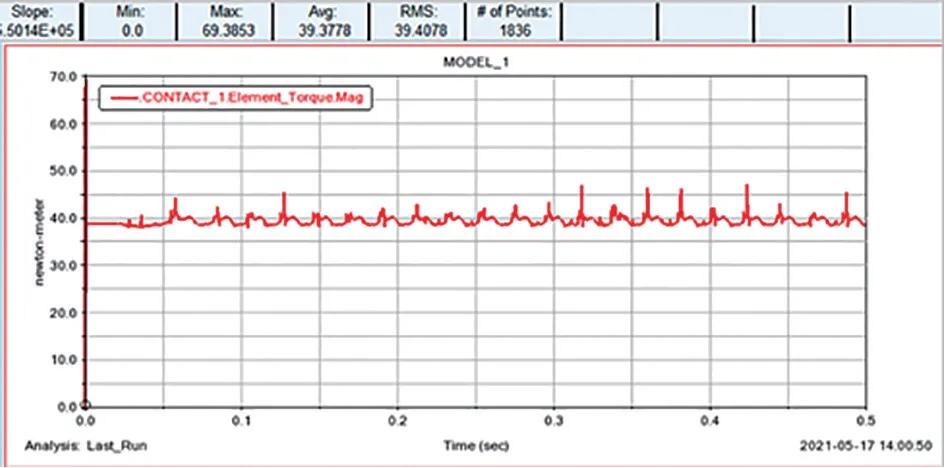
圖5 齒輪轉矩曲線圖

對數據結果進行分析，如表3 所示。

表3

4.2.3 嚙合齒輪柔性耦合仿真

柔性耦合齒輪仿真分析，如圖6 所示。查看轉矩情況，轉矩曲線基本呈直線狀態，在0-0.1 秒的傳動中，轉矩最大值為403.88N/m，平均值為37.20N/m，如圖7 所示。

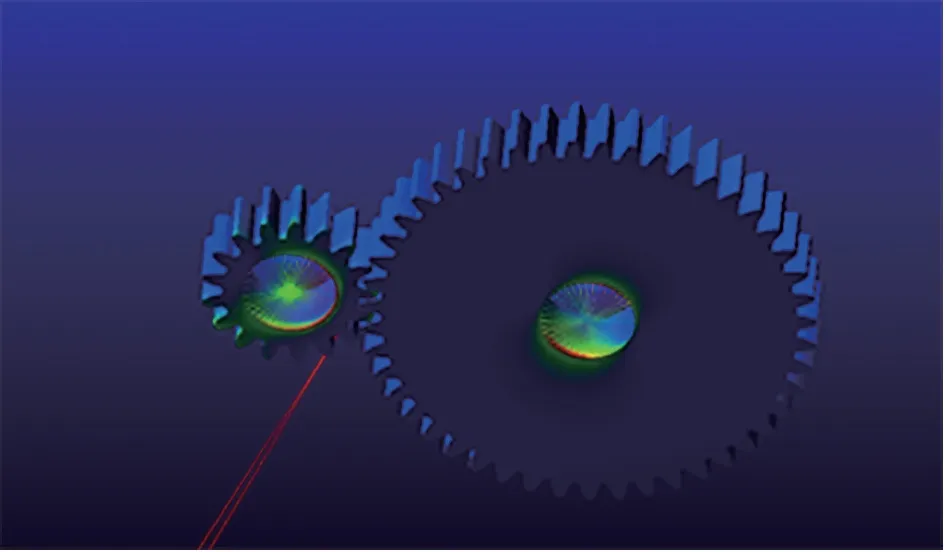
圖6 齒輪柔性耦合仿真

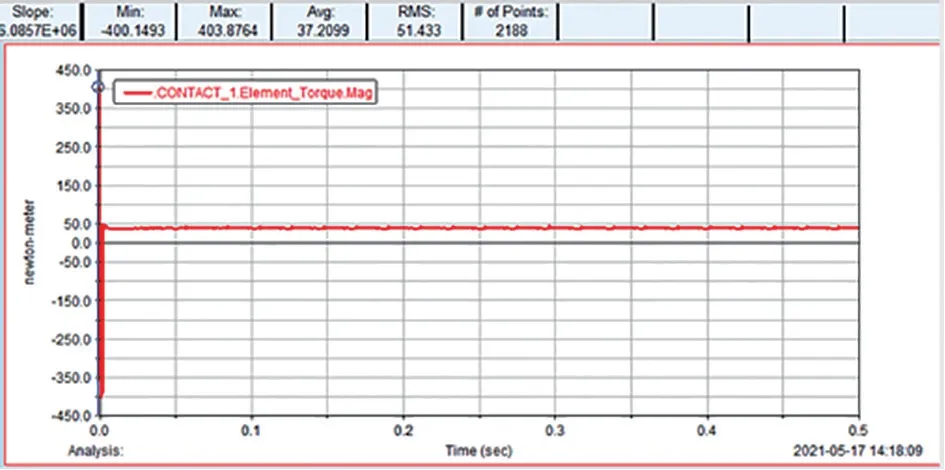
圖7 齒輪轉矩曲線圖

表4

4.2.4 結果分析

通過嚙合力和轉矩的理論計算得到理論值為1810.77N 與33.90N/m，將數值代入誤差計算中，結果如表5所示。

表5

通過曲線圖得知，齒輪在進行嚙合時，剛性耦合模型碰撞最大，其次到剛柔耦合模型，最小是柔性耦合模型，說明柔性耦合模型在齒輪傳動過程中是最平穩的；無論是剛性耦合還是剛柔耦合，柔性耦合模型是最接近理論值的；因此，柔性齒輪嚙合傳動更合乎齒輪的傳動特性。

5 齒輪拓撲優化

本次拓撲優化的載荷條件的設置是基于齒輪三種耦合模型的動力學仿真，在齒輪的動力學仿真中已經證實柔性齒輪是最符合實際的，柔性齒輪可以通過其優越的彈性形變能力吸收部分碰撞能量，從而達到減輕碰撞的效果，所以考慮以柔性耦合的最大輸出轉矩作為拓撲優化的邊界條件，柔性耦合模型中的最大輸出轉矩為403.88N/m。

賦予齒輪材料屬性為45 號鋼，先劃分2D 網格，再對網格進行拉伸，手動劃分的網格可以對輪齒處進行細化，可以提高有限元分析的準確性；在齒輪內圈施加剛性接觸，約束剛性單元，僅開放繞軸的自由度，對其中一個輪齒面施加固定約束，如圖8 所示。添加設計變量為design，考慮到在求解過程中載荷分布不均會導致優化后的材料分布不均，結構混亂，故要添加一個豎直方向的拔模約束和周向對稱的幾何約束，響應量為柔度響應com 與體積響應vol，設置工況以后定義優化以后的體積分數為70%，即保留30%的體積，優化結果如圖9 所示。

圖8 有限元分析模型

圖9 齒輪拓撲優化

拓撲優化前后質量變化（kg）如表6 所示。

表6

6 齒輪靜力學分析

在拓撲優化完成后我們需要對優化前后的齒輪模型做一個強度對比，此項工作是基于嚙合齒輪的動力學仿真，以齒輪嚙合傳動時所受到的圓周力、徑向力為載荷條件，以應力、振動位移為研究對象。

齒輪所受到的徑向力與圓周力。現計算在動力學仿真中齒輪所受到的徑向力與圓周力大小，徑向力與圓周力的公式為

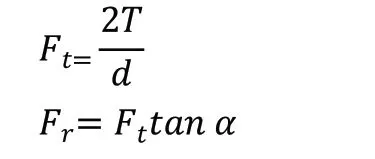
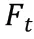
故可以得到徑向力為115.02N，圓周力為316.08N。至此，分析的載荷條件已經計算完畢。現對齒輪進行載荷的施加，對軸心處的剛性連接點施加固定約束，對其中一個輪齒施加圓周力與徑向力，如圖10 所示。

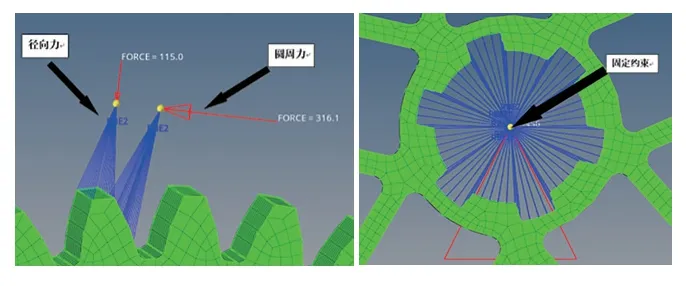
圖10 邊界條件施加

查看位移云圖，最大位移量為0.07mm，作用在輪齒處，如圖11 所示；查看應力云圖，最大應力為318Mp，作用在齒根處，如圖12所示；從結果可以看出，位移量可以忽略不計，最大應力不超過45 號鋼的屈服強度，說明拓撲優化的合理性。

圖11 位移云圖

圖12 應力云圖

7 結論

在齒輪副的動力學仿真中，通過剛性耦合、剛柔耦合、柔性耦合模型的仿真對比，柔性體相對于剛性體的誤差明顯減小，分析結果與理論計算比較接近，可以發現齒輪柔性化后得到的數據更為準確，能夠使齒輪拓撲優化的準確性提高，更為接近實際值，對于齒輪的拓撲優化有更大的提升空間。