時間尺度上具有次線性中立項的三階Emden-Fowler時滯動力方程的振動性
仉志余, 馮瑞華
(1. 太原工業學院理學系,太原 030008; 2. 中北大學理學院,太原 030051)
0 引言
本文研究時間尺度T 上具有次線性中立項的Emden-Fowler 時滯動力方程
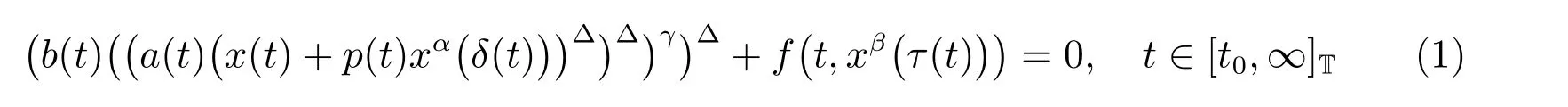
的振動性。除非特殊聲明,下面的假設總成立:
(A1)a(t)> 0, b(t)> 0, p(t)≥0, q(t)> 0 是定義在[t0,∞)T= [t0,∞]∩T 上的實值右稠連續函數,連續函數f(t,u)滿足f(t,u)/u ≥q(t), u ?= 0,并有a?(t)≤0,0≤p(t)≤p<1;
(A2)α、β、γ均為兩個正奇數之比的常數且0<α ≤1, γ ≤β;
(A3)δ(t)和τ(t)是定義在[t0,∞)T上的時滯函數,滿足τ(t)≤t, δ(t)≤t,且有τ?(t)>0,limt→+∞τ(t)=limt→+∞δ(t)=∞。

本文將分別在兩種情況下建立方程(1)的振動定理。
本文僅考慮方程(1)的非平凡解x(t),即對于一切T ≥Tx ≥t0,使得sup{|x(t)|:t ∈[T,∞)T}>0 的解。因為我們研究的是方程解的振動性,所以假設時間尺度T 是無界的。如果x(t)既不是最終正解,也不是最終負解,則稱x(t)為振動的,否則稱x(t)為非振動的。如果方程(1)的每一個解都是振動的,則稱其為振動的,否則稱為非振動的。
人們對于時間尺度上時滯動力方程振動性研究的興趣經久不衰,這是因為它們有著廣泛的工程背景和應用價值,可見文獻[1—4]所述。而在科學工程等領域的應用研究中時滯現象是普遍存在的,據文獻[2]可知,在研究控制理論、物理學、電動力學以及光學等非線性系統的定性、定量行為時,建立的數學模型都需要考慮“時滯”現象。如在自動控制的裝置中,從輸入信號到接收到反饋信號,必然要有一段時間滯后;又如生物醫學中一些傳染病模型等也具有時滯現象;再如橋梁等建筑物體受外力沖擊產生的振動和車輛行駛中產生的振動都有時滯現象。因此,需建立中立型時滯動力方程模型進行刻畫。除此之外,還需要考慮系統的離散性引起的影響。總之,時間尺度上的動力方程理論就能更好地解決這些困難,使我們更好地理解連續系統與離散系統以及其他復雜系統的本質特征。因此,研究時間尺度上中立型時滯動力方程的振動性具有廣泛的應用價值。
關于中立型時滯動力方程及其中立項的類型,一般按其難度是從線性到非線性的。次線性和超線性是非線性的常見類型。具有線性中立項的二階方程的振動性研究成果已相當豐富[5–9],但具有次線性或超線性中立項的研究成果因受其難度的影響就比較少見[10–14]。例如,2007 年,Lin 和Tang[11]研究一階具有超線性中立項的微分方程
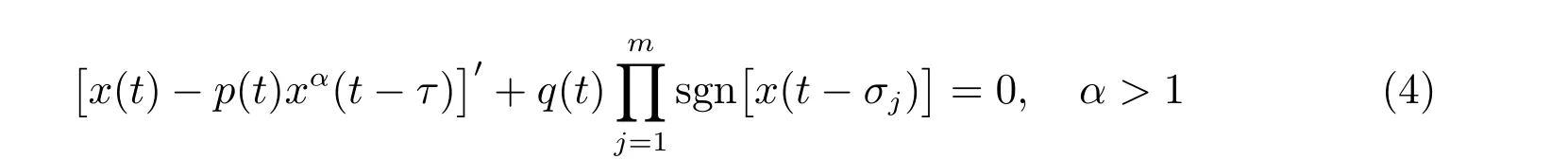
的振動性。2014 年,Agarwal 等[12]研究了一類具有次線性中立項的二階時滯微分方程

的振動性,這里0<α ≤1 是兩個正奇數的比。2017 年,Tamilvanan 等[13]研究了具有次線性中立項的二階非線性微分方程

的振動性,這里α和β是兩個正奇數的比值。2018 年,Grace 和Graef[14]巧妙地運用了不等式技術也研究方程(6)的振動性,并得到了方程振動的充分條件。
由于三階中立型動力方程的振動性情形更為復雜,所以其研究成果如文獻[3,4,15—22]遠沒有一二階的那么豐富,其中具有次線性中立項的也只有文獻[21—22],他們研究的是一類具有次線性中立項的三階時滯微分方程
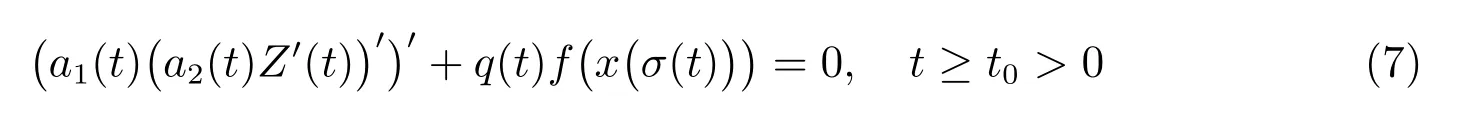
的振動性,其中Z(t) =x(t)+p(t)xα(τ(t)),0<α ≤1 是兩正奇數的比。ai(t)(i=1,2)、p(t)、q(t)是正實值連續函數,τ(t)、σ(t)是時滯函數,滿足τ(t)≤t, σ(t)≤t且limt→+∞τ(t) = limt→+∞σ(t) =∞。此外,函數f(u)非減且對于u ?= 0 存在常數k滿足uf(u)≥k> 0。他們分別得到了如下兩個振動定理,即文獻[22]中定理1 和定理2。
定理1 設0 成立。如果存在一個正值函數? ∈C1([t0,∞),R),使得對任意常數M> 0 和所有足夠大的t3>t2>t1>t0,有 成立,其中 則方程(7)的每個解x(t)振動或者limt→∞x(t)=0。 定理2 設0 成立。如果存在一個正值函數? ∈C1([t0,∞),R),使得對任意常數M> 0 和所有足夠大的t3>t2>t1>t0,有(9)式、(10)式和 成立,其中 則方程(7)的每一個解x(t)振動或者limt→∞x(t)=0。 對于時間尺度上三階中立型動力方程振動性研究也只見到中立項是線性,即α=1 的情形。如2014 年,Candan[18]研究了時間尺度上具有線性中立項的三階非線性時滯動力方程 的振動性,這里0≤p(t)≤p< 1, γ ≥1 是兩個正奇數的比,r1(t)、r2(t)、p(t)是正實值右稠連續函數,τ(t)、δ(t)是時滯函數滿足τ(t)≤t, δ(t)≤t且有limt→+∞τ(t) =limt→+∞δ(t)=∞和δ?(t)>0 成立。此外,連續函數f:T×R→R 滿足對所有u ?=0 都有uf(t,u)> 0,且存在正實值右稠連續函數q(t),使得|f(t,u)|≥q(t)|uγ|。文獻[18]得到了多個振動定理,現將其中定理2.1 和定理2.2 改述為下面的定理。 定理3 設δ(σ(t))=σ(δ(t)),其中σ(t)特指時間尺度T 的右跳算子。如果 成立,其中Q(s)=q(s)(1?p(s))γ,則方程(13)的每個解y(t)振動或limt→∞y(t)=0。 定理4 設δ(σ(t)) =σ(δ(t))且(14)和(15)式成立,若存在一個正實值右稠連續且?可微函數α(t),使得 則方程(13)的每個解y(t)振動或者limt→∞y(t)=0。 顯然,方程(7)和(13)都是方程(1)的特例。受到文獻[18]關于處理時間尺度和文獻[21—22]關于處理次線性中立項方法的啟發,我們利用不同于文獻[21—22]的不等式方法研究方程(1)分別在(2)式和(3)式情況下的振動性,拓展并改進上述已有結果。 為了方便引入下面的記號 引理1[5]如果A>0, B ≥0, u>0,則有 而當且僅當B=A時上式等號成立。 引理2 設x(t)是方程(1)的最終正解且(2)式成立,則z(t)有且僅有以下兩種情形之一: (I)z(t)>0, z?(t)>0,(a(t)z?(t))?>0,(b(t)((a(t)z?(t))?)γ)?<0; (II)z(t)>0, z?(t)<0,(a(t)z?(t))?>0,(b(t)((a(t)z?(t))?)γ)?<0。 證明 證明過程與文獻[18]中的引理1 類似,故省略。 引理3 設x(t)是方程(1)的最終正解且(3)式成立,則z(t)有且僅有(I)、(II)和: (III)z(t)> 0, z?(t)> 0,(a(t)z?(t))?< 0,(b(t)((a(t)z?(t))?)γ)?< 0,三種情形之一。 證明 證明過程與文獻[22]中的定理2 類似,故省略。 引理4 設z(t)滿足引理2 的情形(I)且a?(t)≤0 和 所以可得z??(t)>0。 令Z(t)=z(t)?tz?(t),有 可知Z(t)在[t1,∞)T上是嚴格單調減的。可以斷言,存在t2∈[t1,∞)T,當t ∈[t2,∞)T時,Z(t)>0。否則若Z(t)<0,于是 從而,有z(τ(t))≥Lτ(t)。由于z(t)> 0, z?(t)> 0, z??(t)> 0,可知z(t)是無界的,所以x(t)也是無界的。于是,存在常數P> 0,使得x(t)≥Pz(t)。進而有x(τ(t))≥Pz(τ(t))。所以將其代入方程(1),得 對上式從t3到t積分,有 可得(21)式成立,從而有 即(22)式成立。 定理5 設(2)式成立,若存在可微函數ρ(t)∈(T,R),使得對任意常數M ∈(0,1](當α=1 或β=γ時,M=1)和所有足夠大的t1≥t0>0,均有 則方程(1)的每個解x(t)振動或者limt→∞x(t)=0。 證明 設方程(1)在[t0,∞)T上有一個非振動解x(t),不妨設最終為正(最終為負時,可類似證明),且存在t1∈[t0,∞)T,使得t ∈[t1,∞)T時,有x(t)> 0, x(τ(t))>0, x(δ(t))>0。由引理2 知,z(t)存在兩種可能的情形。 假設z(t)滿足情形(I),則當t>t1時,有z(t)> 0, z(τ(t))> 0, z(δ(t))> 0。因為z(t)在[t1,∞)T是單調增的,所以有z(t)>M0=min{z(t1),1}∈(0,1],從而有 顯然,當α=1 時,在上式中取M0=1 仍成立。從而有 將(25)式代入方程(1),有 定義Riccati 變換 顯然,有ω(t)>0,由時間尺度上積與商的求導法則及(26)式、(27)式,可得 從而,有 其中 根據Keller 鏈鎖法則公式(可見文獻[4]引理1)并注意到這里z?(t)>0,有 于是,當β>1 時,有 令 將上式代入(28)式并注意到(22)式和(27)式,則 由z(t)在[t1,∞)T是單調增的,知z(t1) 當0<β ≤1 時,由(29)式知 因此,將上式代入(28)式,有 再將z(τ(σ(t)))>M0代入上式,得 根據c(t)的定義,合并(31)和(32)兩式,得 根據不等式(18),在(33)式中令 這與(23)式矛盾。 于是,有x(τ(t))>kz(τ(t)),將其代入方程(1),得 對上式從t到∞積分,并注意到zβ(τ(t))≥lβ,可得 進而,有 再對上式從t到∞積分,得 又對上式從t1到∞積分,有 這與(24)式矛盾,則l=0。故有limt→∞x(t)=0。 注1 由定理5 知,選擇不同的函數ρ(t),可得到方程(1)多個不同的振動定理,這里不一一列出了。特別指出,當ρ(t) = 1, α= 1, γ=β時,可得定理3。因此,本文定理5 已包含了文獻[18]中的定理2.1。 注2 當α= 1, β=γ時,方程(1)退化為方程(13),即使此時本文定理5 也包含了定理4 即文獻[18]中的定理2.2,因為定理4 中的R2(t,t1)就是本文的B(t,t1)。 注3 即使當T=R, γ=β=1,方程(1)退化為方程(7)時,本文定理5 比定理1 即文獻[22]中的定理1 更簡潔,且這里已將文獻[22]中的任意常數M> 0 改進為任意常數M ∈(0,1],γ=β=1 拓展為β ≥γ>0。 定理6 設(3)式、(23)式和(24)式成立。若對于足夠大的t1>t0,還有 成立,其中 則方程(1)的每個解x(t)振動或者limt→∞x(t)=0。 證明 設方程(1)在[t0,∞)T上有一個非振動解x(t),不妨設最終為正(最終為負時,可類似證明),則存在t1∈[t0,∞)T,使得t ∈[t1,∞)T時,有x(t)> 0, x(τ(t))>0, x(δ(t))> 0,由引理3 知z(t)存在三種可能情形。假設z(t)滿足情形(I)或者情形(II),則與定理5 的證明相同得方程(1)的解x(t)振動或者limt→∞x(t)=0。 假設z(t)滿足情形(III),則a(t)z?(t)> 0, b(t)((a(t)z?(t))?)γ在[t1,∞)T上是單調減,所以,對l>t ≥t1,有 從而,有 若令 則有 對V(t)求導并注意到(26)式成立,則得 將上式代入(36)式,得 當0<γ ≤1 時,根據Keller 鏈鎖法則公式(類似于(29)式),有 將上式代入(39)式,得 其中 將(38)式代入上式,并注意到V(t)<0,得 即有 因為z(t)> 0 單調增,B(t)> 0 單調減且趨于0,所以存在t2≥ t1,使得當t ∈[t2,∞)T時,有z(t)≥B(t),從而有 又由(41)和(42)式,可得 將上式代入(40)式,得 當γ>1 時,類似于(43)式的推導,可得 在上式中,以s代替t,兩邊同乘以Bγ(σ(s)),并對s從t2到t積分,得 對(44)式左邊用分部積分,可得 對于上式中的(Bγ(s))?利用Keller 鏈鎖法則,注意到這時B?(s)≤0,有 當0<γ ≤1 時,由上式以及(44)和(45)式,同時注意到V(s)<0,可得 根據不等式(18),在(46)式中取 因此,有 將上式代入(46)式,并注意到(35)式,得 顯然這與(34)式矛盾。 當γ>1 時,與(46)式證明類似,可得 在(47)式中令 再次利用不等式(18),得 將上式代入(47)式,有 顯然這與(34)式矛盾。 注4 同注3 知,當T = R, γ=β= 1 時,(34)式就是(12)式,且M ∈(0,1]更精細。因此,本文定理6 包含并改進了定理2 即文獻[21]中的定理1 和文獻[22]中的定理2。 例1 考慮時間尺度T 上具有次線性中立項的三階非線性時滯動力方程 取ρ(t)=1 時,有 亦即(24)式成立。因此,由定理5 知,方程(48)在[1,∞)T上的解x(t)振動或者limt→∞x(t)=0。 但顯然定理3 和定理4 對方程(48)無效,因為這里γ ?=β。 例2 考慮時間尺度T 上具有次線性中立項的三階非線性時滯動力方程 所以(51)式成立,從而根據定理6 知,方程(50)的解x(t)在[1,∞)上是振動的或limt→∞x(t)=0。 但是,即使當T = R 時,定理2 即文獻[21]定理1,文獻[22]定理2 以及本文所列文獻中的結果均對此例無效。 本文研究了時間尺度上具有次線性中立項的三階Emden-Fowler 時滯動力方程(1)的振動性,利用Riccati 變換和不等式技巧,分別在正則((2)式)和非正則((3)式)條件下建立了方程(1)的新振動準則定理5 和定理6,所得結果包含和改進了以往文獻的相應結果,最后列舉應用實例驗證了所得理論結果的有效性。 本文主要的創新點或突破點在于將類似于過往文獻中Candan 方程(13)的α= 1 拓展到了方程(1)的0<α ≤1,這揭示了具有線性中立項(α= 1)和真次線性中立項(0<α< 1)時方程的振動性對函數p(t)的不同要求。前者只需0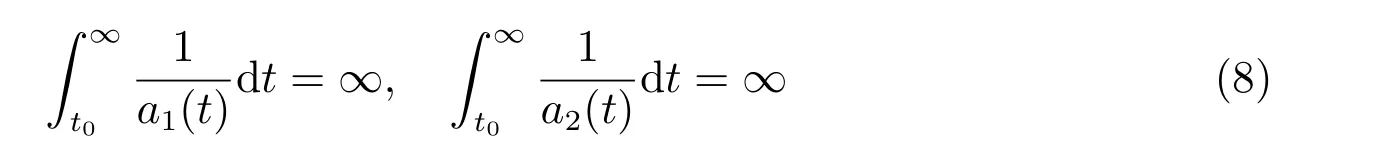

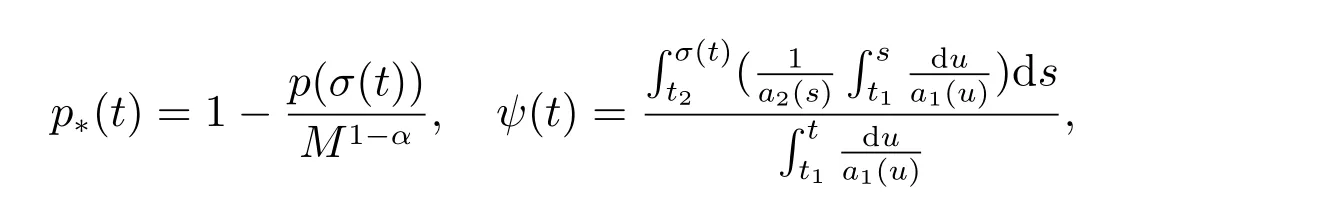
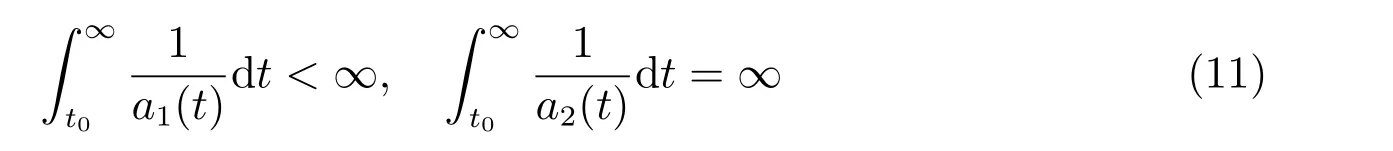




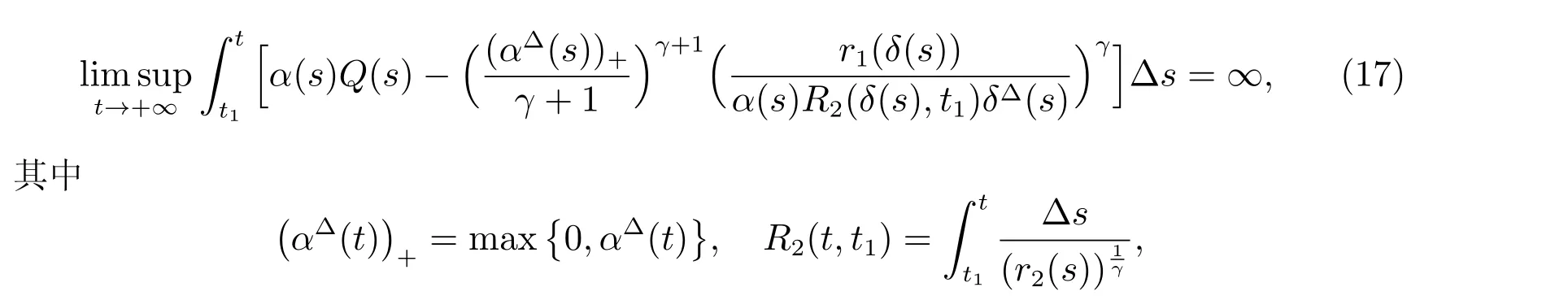

1 重要引理



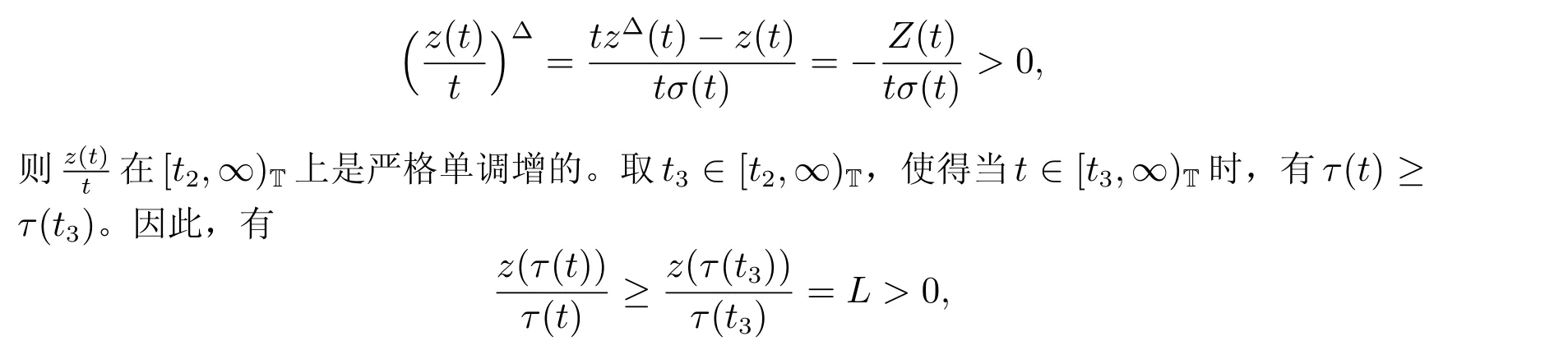
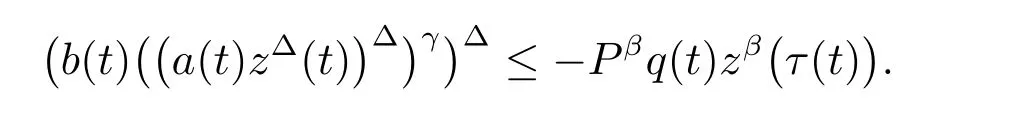
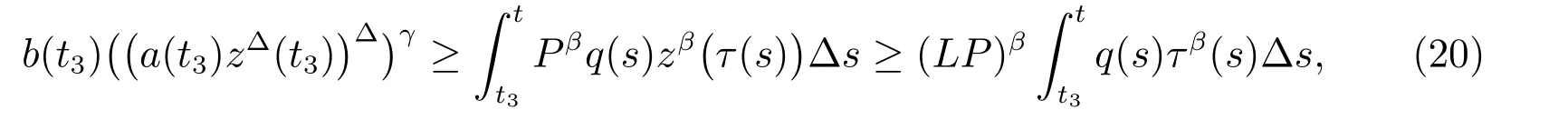


2 主要結果與證明


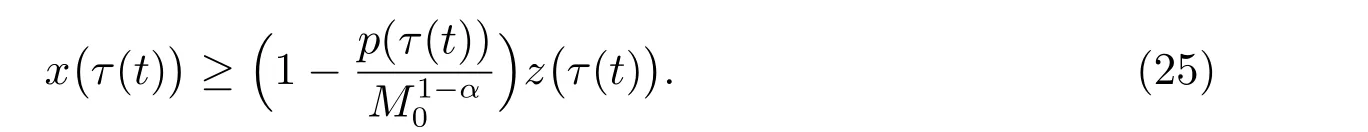


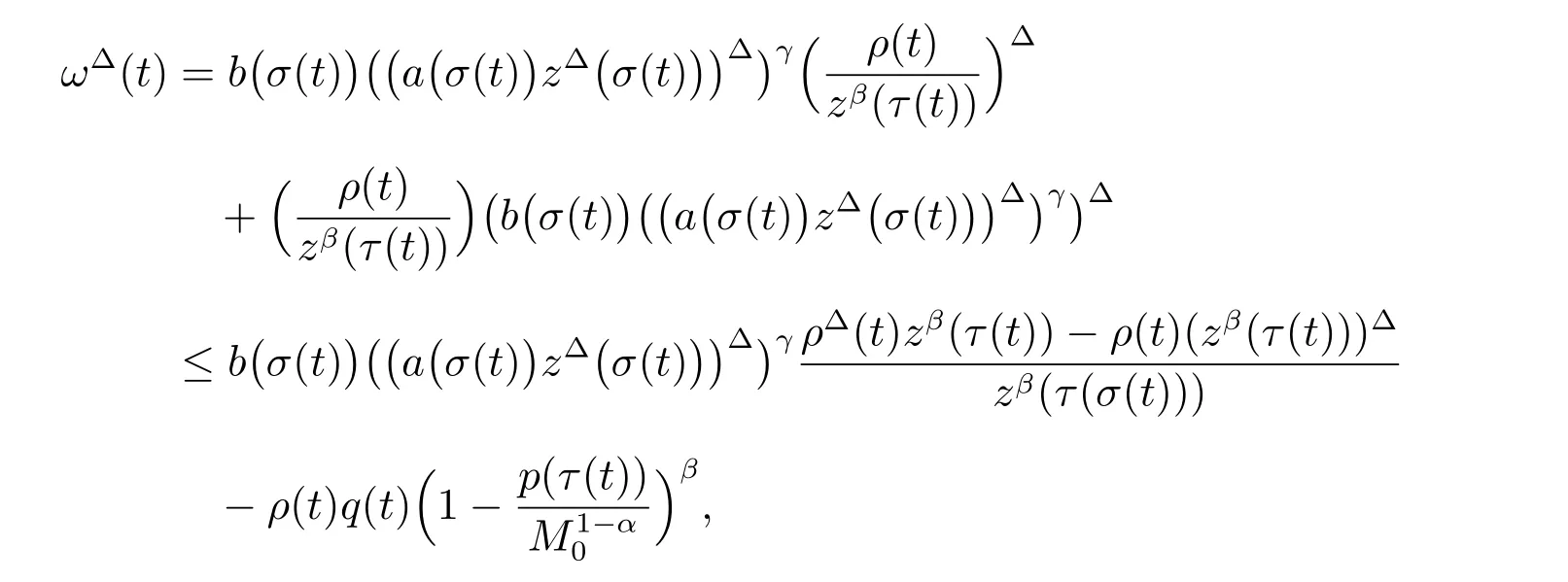
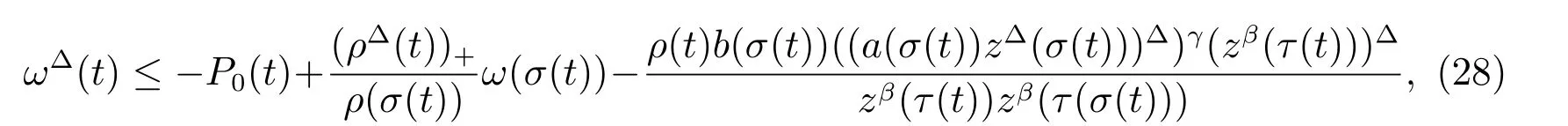




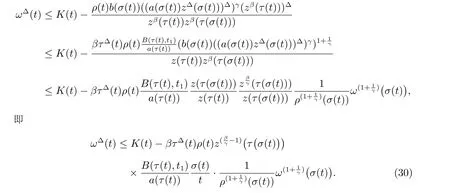

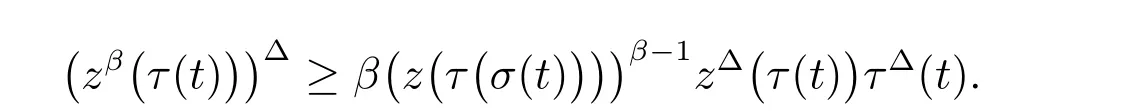

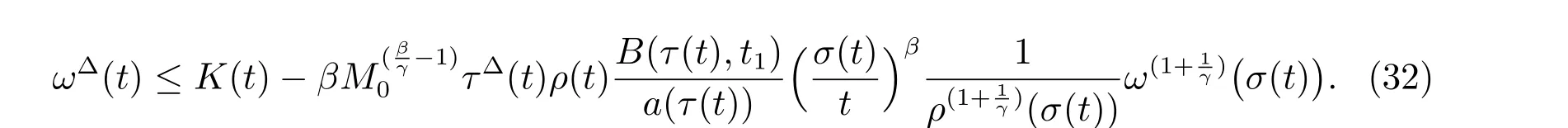
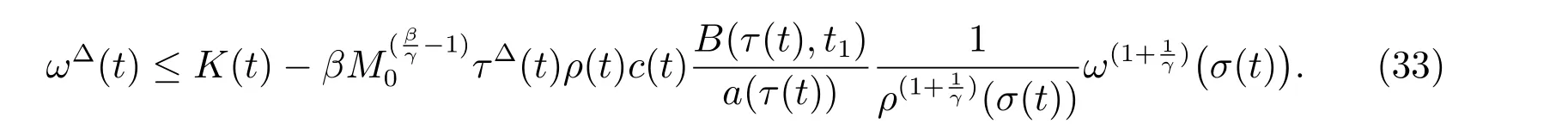



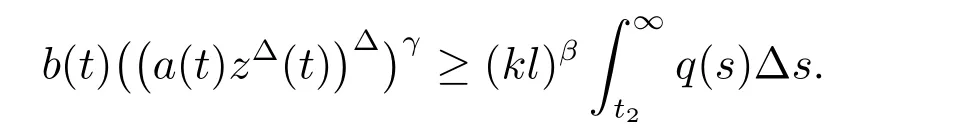



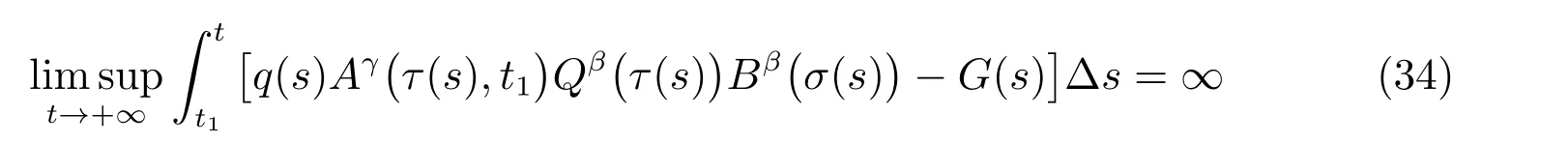


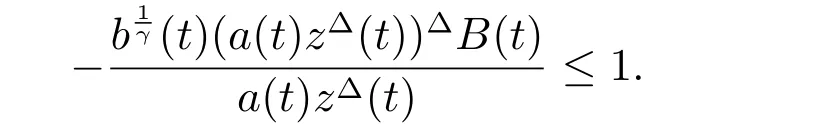

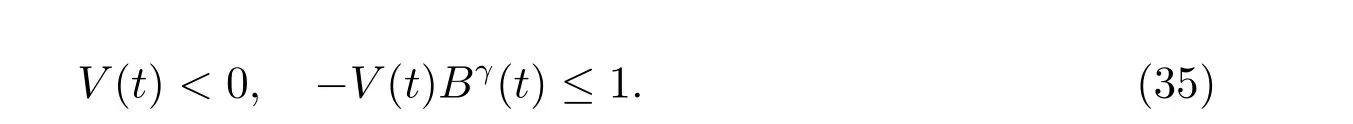




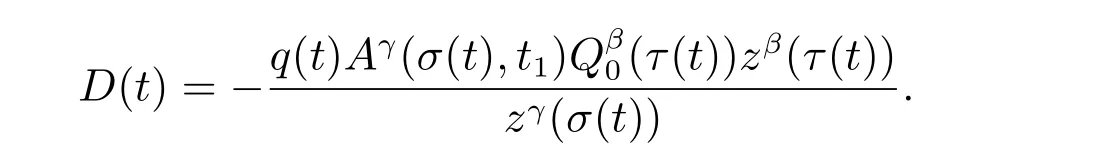
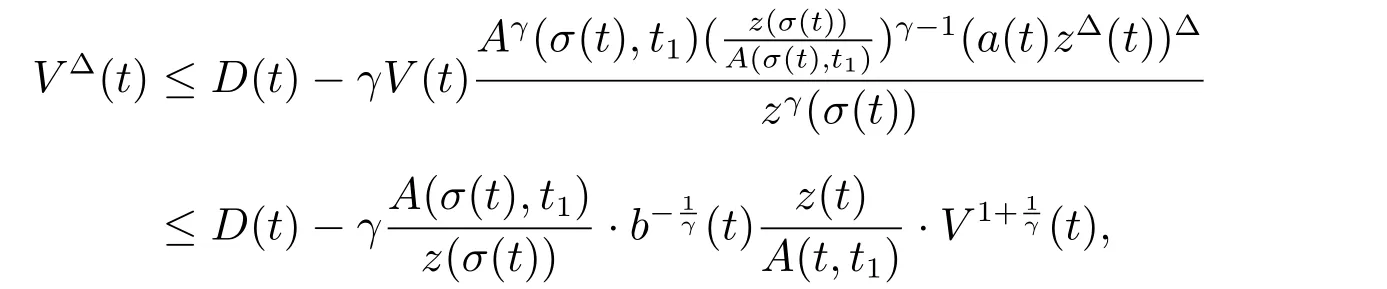







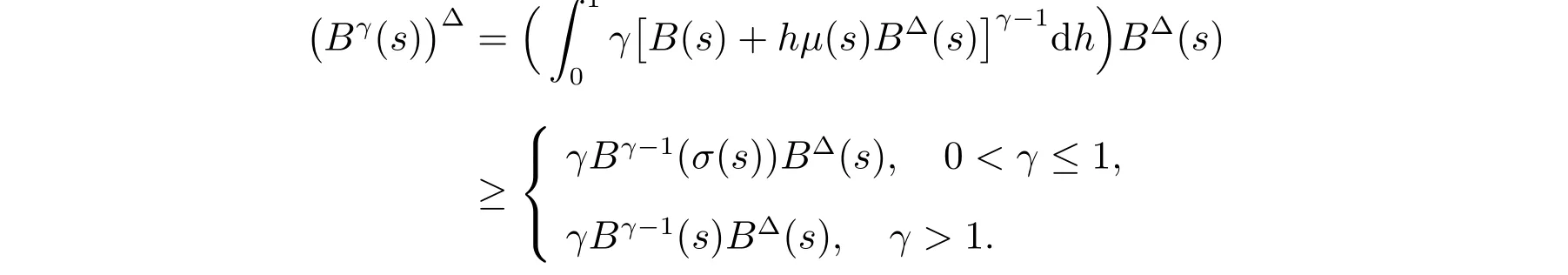







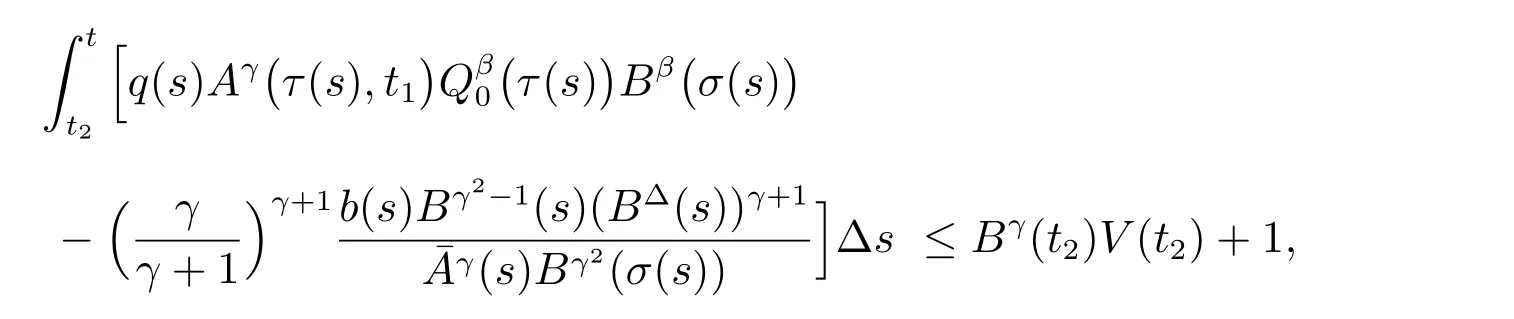
3 應用實例



4 結論

