具有治療和免疫時滯的乙肝病毒模型的穩定性①
沈佳星, 劉賢寧
西南大學 數學與統計學院, 重慶 400715
乙型病毒性肝炎是由乙型肝炎病毒(hepatitis B virus, 簡稱HBV)引起的一種傳染病. 乙肝可分為急性乙型肝炎和慢性乙型肝炎, 慢性乙肝可導致肝硬化和肝癌甚至死亡[1]. 病毒通過接觸感染者的血液或其他體液傳播. HBV入侵人體時, 通過與受體結合的方式進入肝細胞, 然后HBV的DNA被運輸到肝細胞的細胞核中進行復制并排出病毒粒子[2-3].
數學模型在研究和控制HBV傳播中發揮著不可或缺的作用. 自文獻[4]提出一個分析抗病毒治療對減少病原體載量影響的動力學模型后, 許多學者從不同角度建立并分析了HBV動力學模型. 文獻[5-8]研究治療對于減少病毒傳播和抑制病毒傳播的作用. 文獻[9-12]分別研究免疫反應(包括細胞溶解免疫和非細胞溶解免疫)對控制病毒傳播的影響. 文獻[13]考慮了治療和已感染細胞的恢復項. 然而, 文獻[13]沒有考慮感染細胞刺激產生CTL免疫細胞所需時間對動力學分析的影響, 因此, 本文同時考慮了藥物治療和免疫時滯, 建立如下模型:
(1)
其中:x(t),y(t),v(t)和z(t)分別表示未感染細胞濃度、 感染細胞的濃度、 游離病毒濃度和CTL細胞的濃度;Λ表示未感染細胞的產生率;σ表示未感染細胞和感染細胞的死亡率;β表示感染率;u1表示藥物治療阻斷新感染發生的效率;p表示感染肝細胞通過非細胞溶解機制轉移到未感染細胞的恢復率;q表示感染細胞通過免疫介導被殺死的清除率;m表示游離病毒的產生速率;u2表示藥物治療抑制病毒產生的效率;μ表示游離病毒的死亡率;k表示CTL細胞的死亡率;s表示被感染細胞刺激產生CTL細胞的激活率;τ表示細胞免疫時滯.
1 正性和有界性
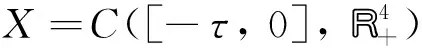
x(θ)=φ1(θ),y(θ)=φ2(θ),v(θ)=φ3(θ),z(θ)=φ4(θ),θ∈[-τ, 0]
(2)
其中:φ=(φ1(θ),φ2(θ),φ3(θ),φ4(θ))∈X,φi(θ)≥0,φi(0)>0,i=1,2,3,4. 根據泛函微分方程的基本理論, 可知系統(1)滿足初值條件(2)有唯一解.
定理1設(x(t),y(t),v(t),z(t))是系統(1)的滿足初始條件(2)的唯一解, 則對任意t>0, 解是正的且有界的.
證首先, 證明y(t)是正的. 假設結論不成立, 即存在t>0, 使得y(t)=0. 令t1=inf{t:t>0,y(t)=0}, 因為y(0)>0, 故y′(t1)≤0. 根據系統(1)的第三個方程, 有y′(t1)=(1-u1)βx(t1)v(t1). 下面證明y′(t1)>0. 由系統(1)的第一個和第三個方程有:
可知x(t1)>0,v(t1)>0, 故y′(t1)>0, 矛盾. 故y(t)為正. 易得x(t),v(t)均為正. 下證z(t)為正. 假設結論不成立, 即存在t>0, 使得z(t)=0. 令t2=inf{t:t>0,z(t)=0}, 則z′(t2)≤0,z(t2)=0. 由τ>0,t2-τ
下證系統(1)解的有界性. 令
沿著系統(1)對t求導
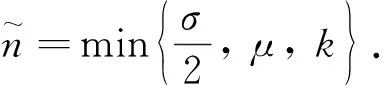
其中ε是任意小的正常數. 故系統(1)的解是有界的.
2 平衡點和基本再生數
利用下一代矩陣法[14], 可得系統(1)的基本再生數和免疫再生數:
下面我們考慮平衡點的存在性, 令系統(1)右邊4個方程為 0, 可得:
當R1>1時, 存在地方病平衡點E2=(x2,y2,v2,z2), 其中
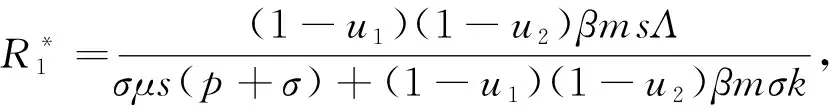
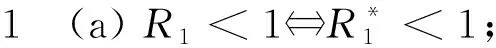

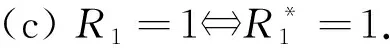
證先證明(a)成立:
類似地, (b)和(c)也成立.
3 平衡點的穩定性
3.1 無病平衡點的穩定性
定理2當R0<1時, 無病平衡點E0局部漸近穩定; 當R0>1時,E0不穩定.
證系統(1)線性化后在E0處的特征方程為
(3)
顯然方程(3)有兩個負特征根λ=-σ,λ=-k. 其它特征根λ滿足方程
(4)
顯然μ+p+σ>0, 當R0<1時,
故方程(4)的兩個特征根實部均為負. 因此, 當R0<1時, 無病平衡點E0局部漸近穩定. 當R0>1時, 方程(4)的兩個特征根實部一正一負, 故E0不穩定.
定理3當R0≤1時, 無病平衡點E0全局漸近穩定.
證定義Lyapunov泛函如下:
沿著系統(1)軌線的全導數為:
當R0≤1時,V′1≤0.V′1=0當且僅當(x,y,v,z)=E0. 因此, {E0}是{(x,y,v,z)|V′1(t)=0}的最大不變集. 根據LaSalle不變集原理, 可知E0全局漸近穩定.
3.2 無免疫平衡點的穩定性
定理4當R1<1
證系統(1)線性化后在E1處的特征方程為
(λ+k-sy1e-λτ)(λ3+K1λ2+K2λ+K3)=0
(5)
其中
對于方程
λ3+K1λ2+K2λ+K3=0
(6)
當R0>1時,y1>0, 故K1,K2,K3均大于0.
由Hurwitz判據法可知方程(6)的特征根均有負實部. 下面考慮方程λ+k-sy1e-λτ=0.
1) 當τ=0時,λ=sy1-k. 定義函數
f(x)對于x求導, 有
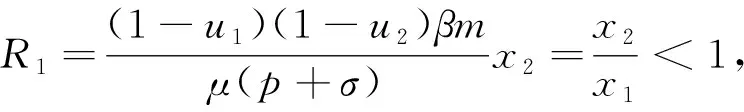
2) 當τ>0時, 假設方程λ+k-sy1e-λτ=0有純虛根λ=±iω(ω>0). 代入并分離實部和虛部有
等式兩邊分別平方再求和有
(7)
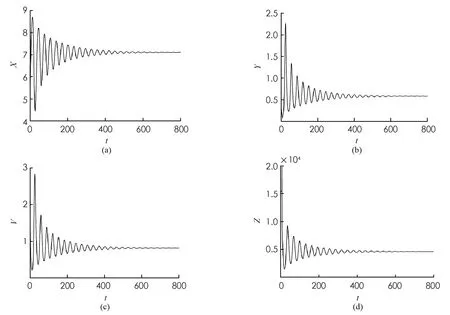
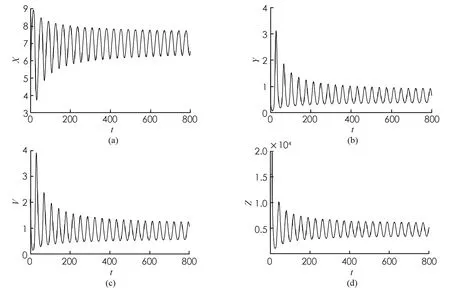
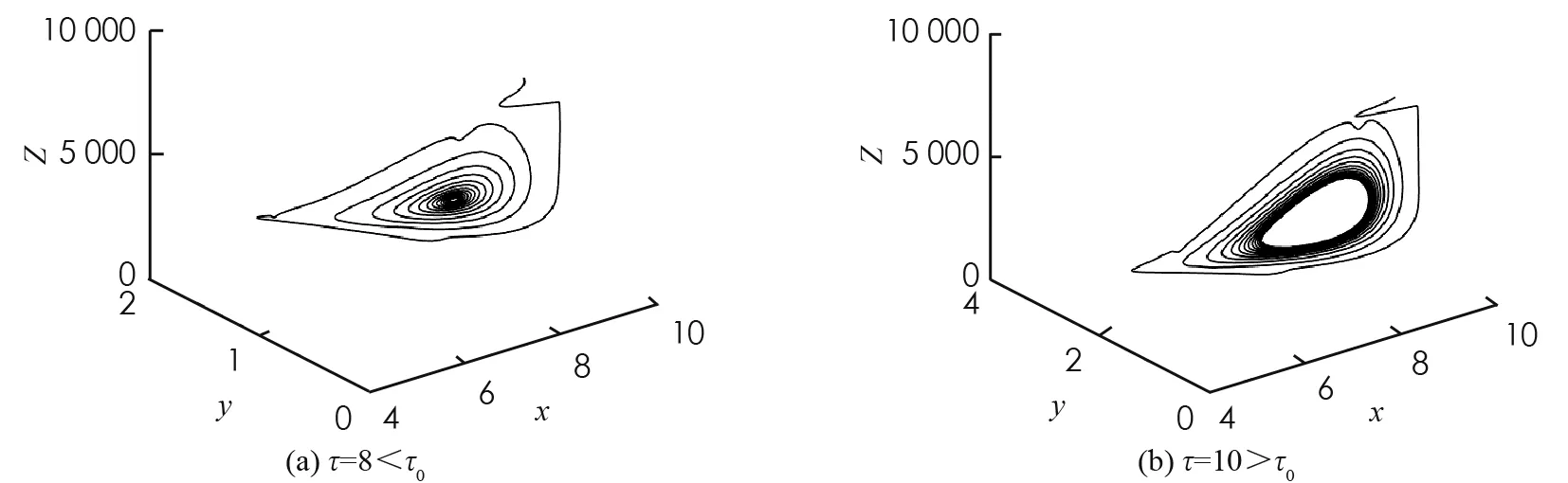
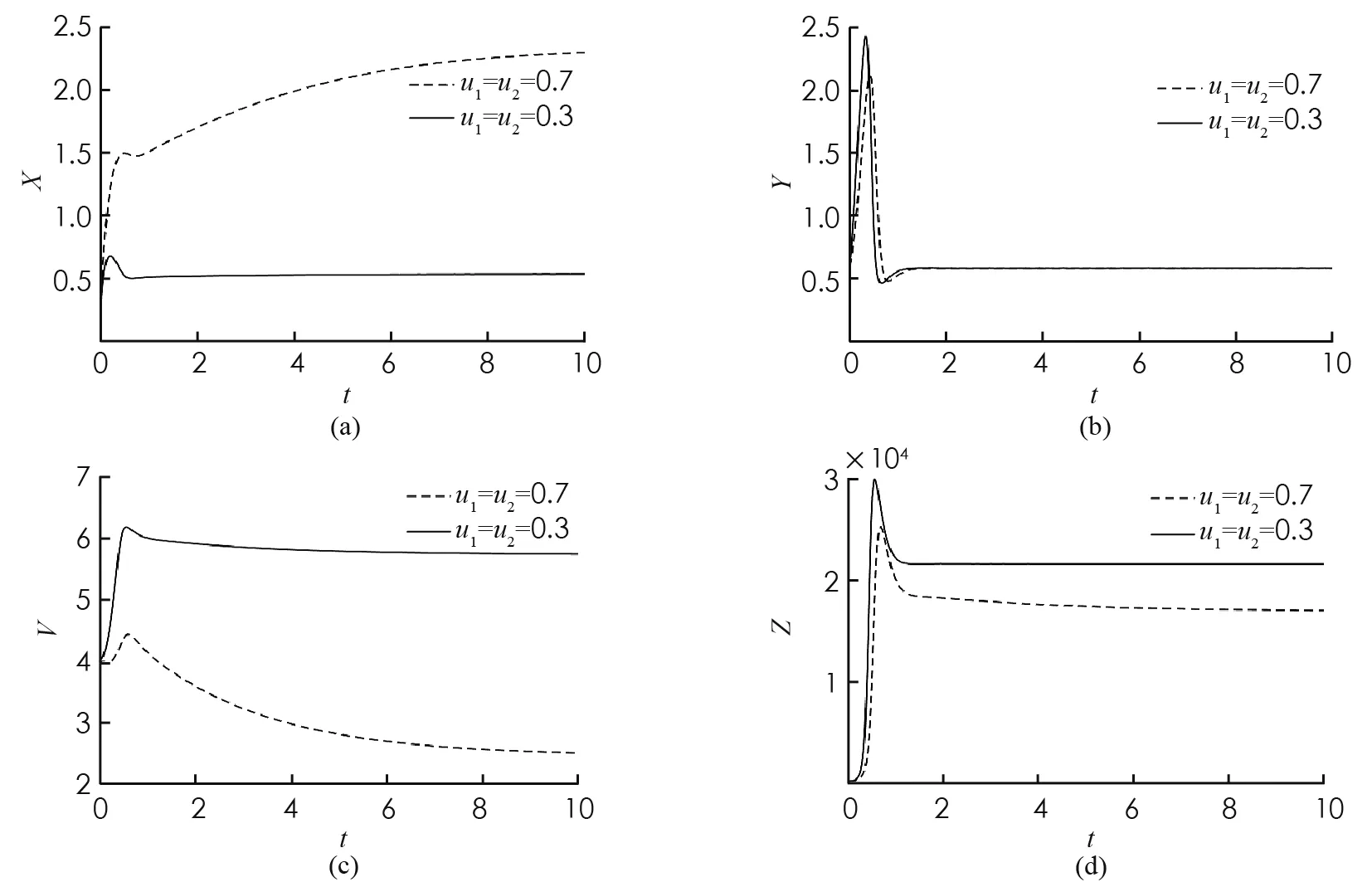
由1)可知, 當R1<1 證定義Lyapunov泛函如下: 沿著系統 (1) 軌線的全導數為: 其中 系統(1)線性化后在E2處的特征方程為 H(λ;τ)=λ4+A1λ3+A2λ2+A3λ+A4+(B1λ3+B2λ2+B3λ+B4)e-λτ=0 (8) 其中 當τ=0時, (8)式變為 H(λ; 0)=λ4+a1λ3+a2λ2+a3λ+a4=0 (9) 其中 當R1>1時,ai>0,i=1,2,3,4. 現在我們考慮當τ>0時, 純虛根的存在性. 假設方程(8)有純虛根iω(ω>0), 代入到方程(8)中有 ω4-A1ω3i-A2ω2+A3ωi+A4=(B1ω3i+B2ω2-B3ωi-B4)(cosωτ-i sinωτ) 分離實部和虛部有 兩邊分別平方再求和, 可得 ω8+H1ω6+H2ω4+H3ω2+H4=0 其中 定義函數 F(x)≡x4+H1x3+H2x2+H3x+H4 因此, 如果方程(8)有純虛根iω(ω>0), 那么方程 F(x)=0 (10) 有正實根ω2. 假設方程(10)有m(1≤m≤4)個正實根, 分別表示為xn(1≤n≤m), 我們有 解出 為了討論系統(1)的Hopf分支存在性問題, 有如下定理: 證方程(8)兩邊對τ求導, 可得 因此有 由Hopf分支理論, 我們有如下定理: 定理81) 當(10)式無正實根時, 對任意的τ≥0, 地方病平衡點E2局部漸近穩定; 3) 當(10)式有正實根時, 系統(1)在τ=τ0處產生Hopf分支. 證1) 結論顯然成立. 2) 根據τ0的定義可知, 當τ∈[0,τ0)時, (10)式沒有正實根, 即特征根沒有穿過虛軸. 所以對所有的τ∈[0,τ0), (8) 式的特征根都具有負實部, 此時E2局部漸近穩定. 為了驗證本文的理論結果, 取文獻[13,15-16]中的數據:Λ=10;β=4.430 1;p=0.12;σ=1.056 1;q=0.000 7;m=5.352 5;μ=0.381 8;s=9.212 9;k=5.375 2. 令u1=u2=0.9. 可計算出R1=3.748 9, 地方病平衡點E2存在且局部漸近穩定,E2=(7.099 3, 0.583 4, 0.817 9, 461.86),τ0=9.704 3. 首先, 考慮解的長期行為. 當τ=8<τ0時, 地方病平衡點局部漸近穩定(圖1); 當τ=10>τ0時, 地方病平衡點不穩定并出現了周期解(圖2); 圖3展示τ=8和τ=10時的相圖. 數值結果與理論結果相一致. 其次, 為了探究藥物治療策略對于控制病毒傳播的影響, 分別取u1=u2=0.7和u1=u2=0.3. 圖4中(a)表明治療效率越高, 未感染細胞濃度的平衡態會明顯增加; (b)表明對于不同的治療效率, 雖然感染細胞濃度最終平衡態相同, 但是藥物治療效率越高, 感染細胞濃度的峰值會有效下降; (c)表明治療效率越高, 自由病毒粒子濃度明顯降低; (d)表示治療效率對降低 CTL 免疫細胞濃度的影響. 圖1 τ=8<τ0時解的時間序列圖 圖2 τ=10>τ0時解的時間序列圖 圖3 取不同時滯時x(t), y(t), z(t)的相圖 圖4 藥物控制措施對于x(t), y(t), v(t), z(t)的影響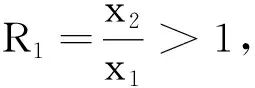

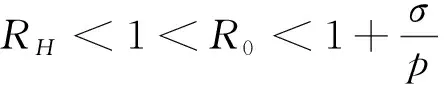
3.3 地方病平衡點的穩定性
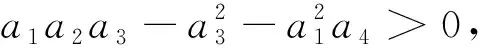
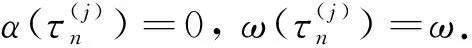
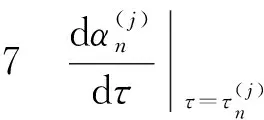
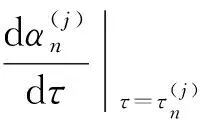
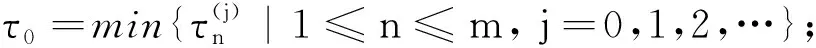

4 數值模擬
5 總結