基于神經網絡的時序約束分解

葉恒舟, 郝 薇, 胡志丹

(桂林理工大學 廣西嵌入式技術與智能系統重點實驗室, 廣西 桂林 541006)

0 引 言

Web服務的數量呈現出幾何倍數的增長, 服務的質量(quality of service, QoS), 特別是時序約束, 顯著影響著Web服務組合的效果。生產性能更好、成本更低，并在更高程度上實現客戶目標的組合服務是十多年來研究的熱點[1]。

QoS約束分解策略是求解時序約束Web服務組合問題的常用方法, 時序約束分解模型的性能決定著相應的服務組合方法的性能。然而, 現有的QoS約束分解模型在不同用戶約束強度下, 并不總能表現良好[2-7]。Guidara等[4]針對時序約束建立了不丟失可靠組合方案的分解模型, 當用戶的約束強度較強時, 該策略可以淘汰相當一部分的候選服務, 從而有效降低問題規模，但當用戶約束強度較弱時, 通過該策略只能淘汰很少的候選服務, 效果很不明顯。文獻[5]提出的時序約束分解模型(TCD)將施加于全局的時序約束分解為針對各個活動或者任務的局部時序約束, 在保證全局時序約束、降低問題規模方面取得了一定的成果，但該模型在用戶約束強度較強時, 可能丟失本就不多的可行組合方案, 導致找不到可行解。文獻[6]提出用戶約束強度感知的時序約束分解模型(CIA-TCD), 它在文獻[5]TCD模型中引入了松弛因子, 并提出了一種基于模糊推理規則的自適應調節松弛因子的方法, 無論用戶約束強度較弱還是較強, 都表現出了較好的性能，但模糊推理規則需要人為設定, 且僅考慮了活動個數、約束強度對松弛因子的影響。

近年來對神經網絡(neural networks, NN)的研究取得了突破性的成果[8-10], 并被廣泛應用于環境污染預測[11]、工業預測[12]、人體監測[13]、市場競爭[14]以及林業估算[15]等重要領域, 起到了關鍵性的作用。針對文獻[6]提出的CIA-TCD模型的不足, 本文使用基于NN的松弛因子自適應調節方法替換基于模糊推理規則的自適應調節方法, 以期避免對人工經驗的依賴, 并增加考慮候選服務個數及約束個數對約束因子的影響。

1 神經網絡模型

1.1 傳播

前向傳播算法將相鄰兩層的神經元節點通過權值連接起來, 前一層的神經元節點，作加權求和及偏移操作后，再作非線性變化得到的結果就是本層神經元節點。神經網絡中每一層神經元都執行該操作, 向前傳播, 最終可得到輸出層的結果。圖1表示了NN前向傳播的原理，即如何由輸入x1、x2、x3、x4獲得輸出y[16]。

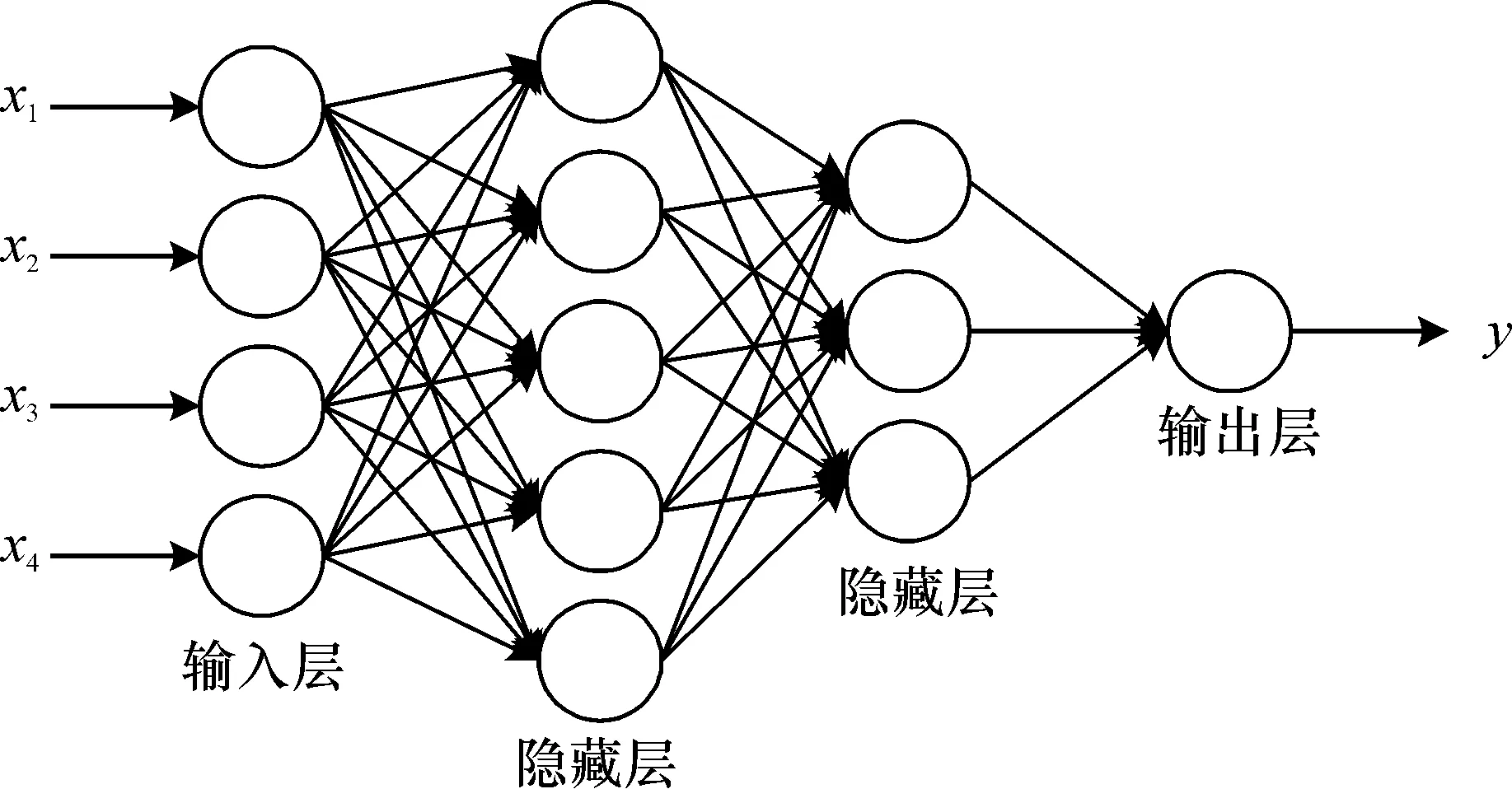
圖1 NN前向傳播原理圖

反向傳播算法的學習過程由信號正向傳播與誤差反向傳播兩個過程組成。正向傳播將輸入信息經輸入層傳入到隱藏層, 經過逐層處理后傳向輸出層, 輸出層對輸出的結果與期望值進行比較, 如果兩者誤差達不到預期目標, 便開啟反向傳播過程, 計算每層目標函數對各神經元權值的偏導數, 即梯度, 作為修改權值的依據。神經網絡中的信號在傳遞的過程中, 權值不斷被修改, 并用一個損失函數權衡輸出值和期望值的差值[17], 當結果與期望值的差值在允許范圍之內時, 停止網絡學習。

1.2 激活函數和損失函數的選擇

在神經網絡學習過程中, 使用激活函數處理每層數據的輸入值, 使得數據每經過一層后都變得更加復雜, 最終結果也會更加精準。激活函數存在各種不同的類型。式(1)所示的Sigmoid函數與其反函數都是單調遞增的, 經常作為神經網絡中閾值函數[18]。

(1)

損失函數計算網絡模型中真實值y與預測值a之間的差異度。損失函數的值越小, 則表示該模型的魯棒性越好。常用的損失函數模型有: 均方差損失函數、交叉熵損失函數、指數損失函數、Hinge損失函數等，這些模型也可以搭配使用, 其中均方差損失函數常與Sigmoid激活函數一起搭配, 形成最小二乘法

(2)

其中:J為損失函數；N為樣本數；yi、ai分別是第i個樣本的標簽值和預測值。

2 約束強度感知的約束分解模型

為有效解決時序約束的服務組合問題, 文獻[5]提出了一種保障時序約束的時序約束分解(TCD)模型, 描述如下:

目標

(3)

約束條件

fk(tc1,tc2, …,tcn)≤τk,k=1, 2, …,r;

(4)

min(Ai.t)≤tci≤max(Ai.t)。

(5)

式(3)描述了TCD模型的優化目標,即，使經過約束分解后剩余的候選組合服務個數最大化。n為工作流中包含的活動個數,第i個活動記為Ai,sij為Ai的第j個候選服務,mi為Ai候選服務個數,sij.t表示sij所需的執行時間,tci為Ai應滿足的時序約束, 即TCD模型的因變量, #B表示集合B中的元素個數。式(4)中,τk(k=1, 2, …,r)為用戶針對整個工作流或某個局部工作流給定的時序約束。fk(tc1,tc2, …,tcn)描述為當Ai(i=1, 2, …,n)選擇所需執行時間為tci的候選服務時, 完成τk針對的工作流所需要的執行時間, 其具體計算方法參考文獻[5]。式(5)約定tci的取值范圍，min(Ai.t)與max(Ai.t)分別表示Ai的候選服務中所需要的執行時間的最小值和最大值。

TCD模型在約束分解階段保障了時序約束, 因而可以使用局部優選策略為每個活動在剩余的候選服務中選擇合適的服務而不違背時序約束。但TCD模型在用戶約束較強時, 容易導致找不到可行解, 原因在于在約束分解階段可能已經淘汰了可行解。為此, 文獻[6]在TCD的基礎上, 提出了一種約束強度感知的時序約束分解模型(CIA-TCD), 其核心思想是在TCD的基礎上引入松弛因子γk(γk≥0,k=1, 2, …,r), 將式(4)改寫為

fk(tc1,tc2, …,tcn)≤(1+γk)τk。

(6)

引入γk后, 實質上放寬了約束分解時的約束條件, 從而可以降低丟失可行解的概率; 同時, CIA-TCD模型不再能保障時序約束, 在后續的優選階段不再能使用局部優選策略, 而是需要全局優選策略, 因而經過約束分解后剩余的組合方案個數不宜過多, 以降低優選階段的時間開銷。

因此, 在確定γk值時, 需要兼顧以下兩個指標:RS和RI。其中：RS表示經過時序約束分解后, 剩余組合方案存在可行解的概率，若用sum表示總測試次數,numavail表示在剩余組合方案存在可行解的次數, 則RS=numavail/sum;RI表示經過時序約束分解后, 由各個活動所保留的候選服務所確定的剩余組合方案個數, 即由式(3)所描述的優化目標。

實驗測試發現,γk的合理取值與工作流的結構、工作流中包含的活動個數、每個活動的候選服務個數、時序約束個數、每個約束所針對的局部工作流中包含的活動個數、每個候選服務的執行時間等諸多因素相關, 亟需尋找確定γk的有效策略。文獻[6]提出了一種基于模糊推理規則的松弛因子自適應調節方法, 通過將活動個數與約束強度模糊化, 結合實驗測試效果, 設計了確定γk的推理規則。該策略考慮的因素較少, 較為依賴經驗數據。為此, 本文提出一種基于神經網絡的松弛因子自適應調節方法。

3 基于NN的松弛因子自適應調節

采用基于NN的松弛因子自適應調節方法替代基于模糊推理規則的松弛因子自適應調節方法是NN-CIA-TCD模型與CIA-TCD模型的主要區別。采用基于NN的松弛因子自適應調節方法, 先通過感知約束強度來控制可找到可行組合方案的概率和剩余組合方案的個數, 逆向求解 NN-CIA-TCD模型, 以獲取包含特征及標簽的訓練數據集, 再建立神經網絡模型, 將訓練集輸入到該模型中進行訓練。考慮到Web服務組合時工作流、時序約束的個數與位置等是不確定的, 為了增強適應性, 在訓練數據集時用于表示組合服務的工作流、時序約束個數、位置等是隨機的, 這就導致在訓練時可能出現分類不合理的標簽, 需要剔除這些標簽。圖2為基于NN的松弛因子自適應調節方法的流程圖。

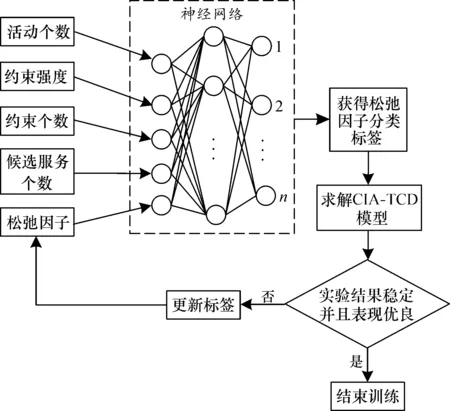
圖2 基于NN的松弛因子自適應調節方法流程圖

3.1 建立樣本庫

在建立樣本庫時, 選擇了4個影響松弛因子取值的因素: 活動個數、候選服務個數、約束強度和約束個數。根據這4個值, 隨機生成一個時序約束組合服務問題, 代入由文獻[6]采用的模糊推理規則確定的松弛因子, 求解相應的TCD模型。若求解結果不理想, 則適當調整松弛因子。通過反復實驗, 最終確定出與這4個影響因素對應的松弛因子的值。

求解結果是否理想, 由RS和RI指標共同確定, 即RS應較大,RI應較小。本文采取的策略是, 若RS≥0.9, 則以恒定步長0.01嘗試減小松弛因子, 直到不能調整, 即一旦調整,RS會小于0.9; 否則，嘗試增大松弛因子, 直到RS≥0.9。

對于一次求解過程, 每個時序約束都對應一個松弛因子, 但考慮施加在局部約束的時序約束具有不確定性, 且容易受到其他約束的影響, 僅保留了全局時序約束對應的松弛因子。式(7)描述了松弛因子的波動范圍, 可以用來對訓練樣本中的松弛因子進行分類

(7)

其中:λT表示分類后的松弛因子;λmax與λmin表示松弛因子的最大、最小值;NT表示的是合適的分類個數。將活動個數、候選服務個數、約束強度和約束個數4個變量和與之對應的λT做成一個樣本, 活動個數、候選服務個數、約束強度和約束個數是特征值,λT作為標簽。改變這4個變量的值, 重復上述工作, 即可形成樣本集。

由于工作流、候選服務集都是隨機的, 在產生樣本時, 同一組特征值, 即活動個數、候選服務個數、約束強度與約束個數均相同時對應的標簽(即松弛因子)可能是不一樣的。在初始產生樣本集時, 每一組特征值對應的樣本記錄都要達到一定的數量。這些記錄中, 若某個標簽出現的次數明顯多于其他, 則選取該標簽; 否則, 去掉最小和最大的標簽后, 取其他標簽的平均值。最終的樣本集中, 每組特征值只對應一個標簽。

3.2 NN分類訓練

由于松弛因子的分類數較多, 需要大量的訓練樣本，為此將樣本庫拆分成若干互斥的子樣本集, 對NN進行迭代更新訓練, 以降低訓練時對設備性能的要求。從各個子樣本中隨機選擇少量樣本形成測試樣本集, 對NN的訓練結果進行測試。測試時若發現訓練結果不滿意, 需要定位并剔除或修改異常樣本, 以更新訓練樣本集。圖3描述了NN分類訓練流程。

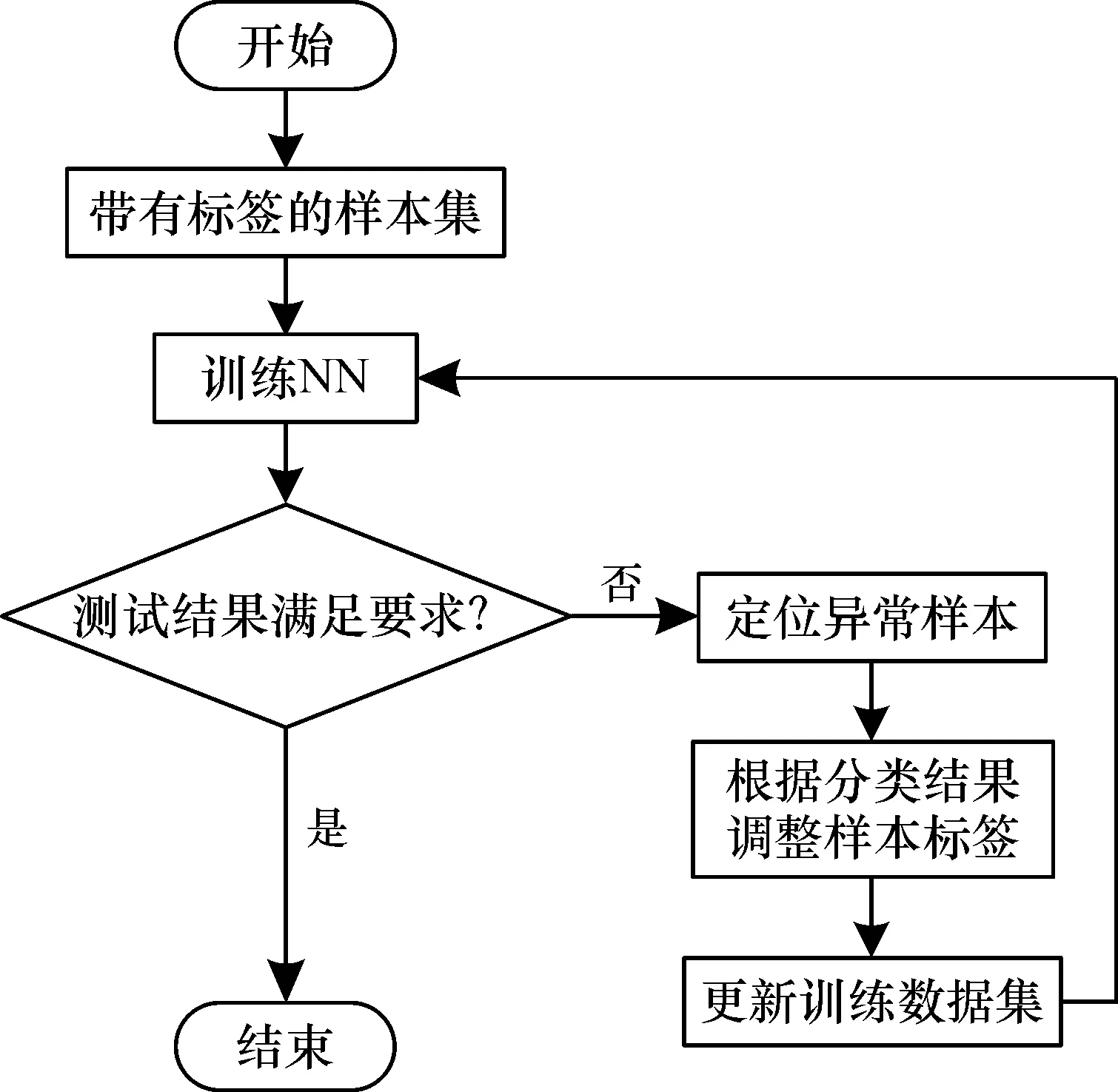
圖3 分類訓練流程圖

4 實驗分析

本實驗運行在配置為Interl(R)Core(TM)i7-3630QM、2.40 GHz CPU、4 GB內存、64位Windows 7操作系統的PC機上, 編程語言為Java 1.8, MATLAB 2017b。實驗中神經網絡共分為3層, 每一層的節點數分別設置為50、100、50, 迭代次數為2 000次。

在仿真實驗中, 通過改變約束強度和服務組合規模(表1), 固定約束個數, 從RS、RI兩個性能指標分析對比約束強度、活動個數以及候選服務個數對TCD模型、CIA-TCD模型和NN-CIA-TCD模型的性能影響。工作流根據活動個數隨機生成, 候選服務的執行時間由QWS數據集[19-20]中的響應時間來模擬。約束強度的變化區間為[-0.8, 0], 步長為0.1。

表1 服務組合規模的設定

4.1 約束強度對RS和RI影響(G1與G2)

G2規模較G1規模增加了每個活動的候選服務個數。圖4給出了在G1、G2規模下, 分別采用TCD、CIA-TCD和NN-CIA-TCD三種模型, 所得到的RS的對比結果。分析可得: 候選服務個數的增加會提高對應模型找到可行組合方案的概率; 約束強度的值變大, 即約束強度變弱時, 3種模型相對應的可找到可行組合方案概率會顯著提高, 但終會趨于平穩; 當約束強度較強時(-0.8～-0.5), 采用NN-CIA-TCD模型較CIA-TCD模型可找到可行解的概率更高, 表現更好, 在約束強度較弱時, NN-CIA-TCD模型也能夠保持較高找到可行組合方案的概率；但當約束強度值位于[-0.5, 0]時, 與CIA-TCD相比, NN-CIA-TCD獲得的RS要低一些。這是因為松弛因子是由兩個指標RS和RI共同確定的，而這兩指標存在沖突。在確定樣本時,RS是以0.9為分界點的, 最終獲得的RS也在0.9附近波動，表明RS與預期一致。雖然NN-CIA-TCD較CIA-TCD在指標RS上要差一些，參照圖5, 但在該區間RI較為穩定, 且明顯低于CIA-TCD。可見在設置NN-CIA-TCD參數值時，傾向于獲得更好的RI。若需要更好的RS, 可以在生成樣本時, 提升RS的分界點。

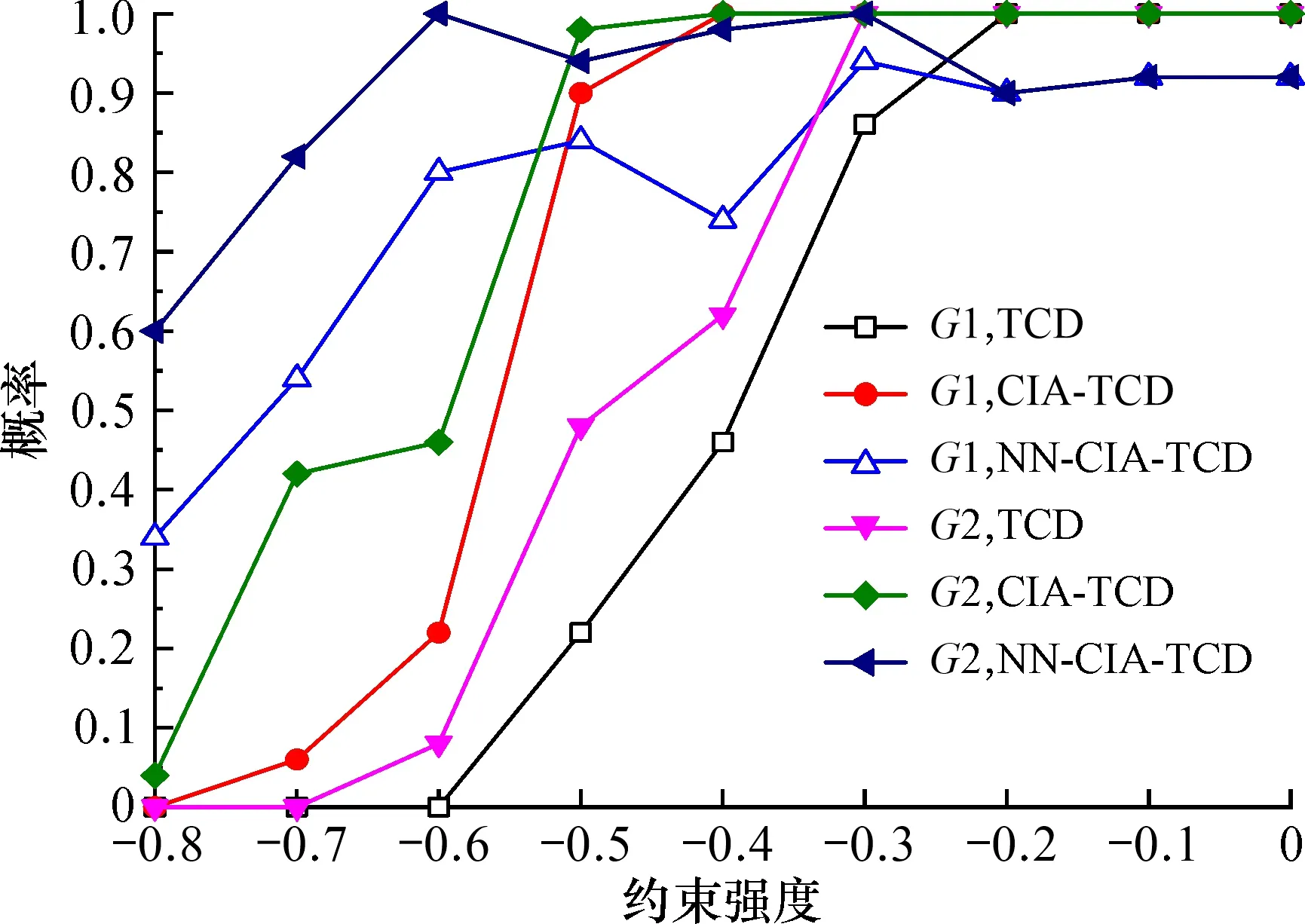
圖4 約束強度對RS的影響對比(G1與G2)

圖5給出了在G1、G2規模下, 3種模型所得到的RI的對比結果。可以發現: 隨著候選服務個數的增加, 采用不同模型時的剩余組合方案個數明顯下降; NN-CIA-TCD模型在約束強度較強時能夠提高剩余組合方案個數, 在約束強度較弱時, 能夠控制剩余組合方案個數; 當約束強度增加時, TCD模型和CIA-TCD模型的剩余組合方案個數的指數值RI都呈現出緩慢上升的趨勢, 只有NN-CIA-TCD模型的值始終趨于穩定。這說明無論約束強度如何, NN-CIA-TCD模型都能維持較為合適的剩余組合方案個數。

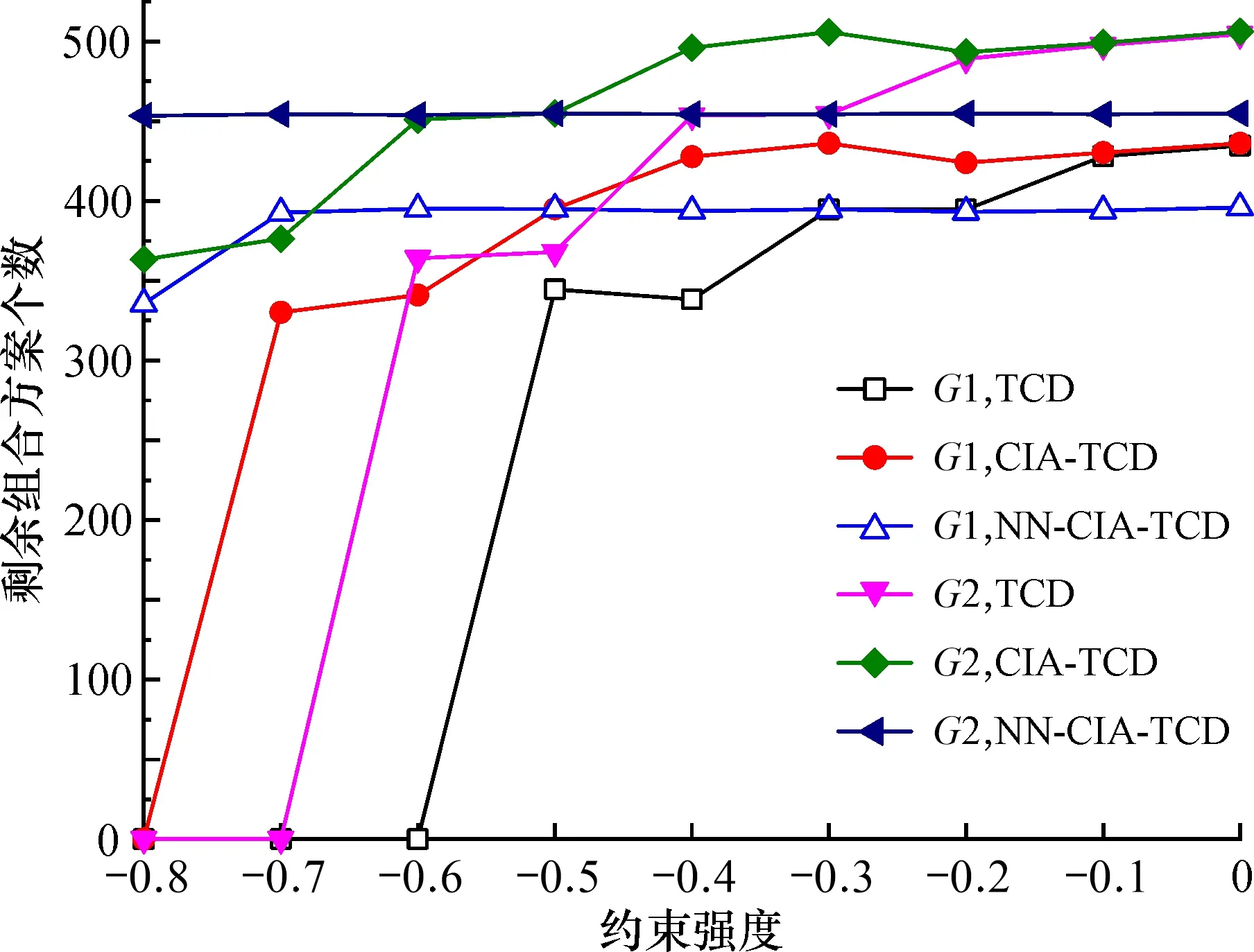
圖5 約束強度對RI的影響對比

4.2 約束強度對RS和RI影響(G1與G3)

G3規模較G1規模增加了活動的個數。圖6給出了在G1、G3規模下, 3種模型所得到的RS的對比結果。可以看出: 隨著活動個數的增加, 模型對應的找到可行組合方案的概率會有小幅度的下降; 當約束強度較強時, TCD模型找到可行組合方案的概率較低, 采用CIA-TCD模型和NN-CIA-TCD模型可以有效提高找到可行組合方案的概率; 當約束強度較弱時, 3種模型都能有較高的找到可行組合方案的概率; 當約束強度和規模相同時, 對比CIA-TCD模型和NN-CIA-TCD模型的RS可以發現, 約束強度較強時(≤0.6), NN-CIA-TCD模型比CIA-TCD模型表現更好。與圖4類似, 由圖6可見，在約束強度位于[-0.5, 0]時, 與CIA-TCD相比, NN-CIA-TCD獲得的RS也要低一些。

圖6 約束強度對RS的影響對比

圖7給出了在G1、G3規模下, 3種模型所得到的RI的對比結果。分析可得: 隨著活動個數的增多, 模型對應的剩余組合方案個數會有大幅度的上升; 當約束強度增加, 規模相同時, TCD模型和CIA-TCD模型的RI都依然呈現緩慢上升的趨勢, 而NN-CIA-TCD模型的剩余組合方案個數的RI值呈現出先上升后一直穩定的趨勢。這說明對于不同約束強度, NN-CIA-TCD模型能夠更快獲得更合理的剩余組合方案個數。

圖7 約束強度對RI的影響對比

5 結束語

在研究時序約束服務組合問題時, 時序約束分解策略受到廣泛關注, 它需要在保障全局約束與有效降低解空間之間取得平衡, 以適合不同強度的用戶約束。通過在現有的保障全局約束的分解模型中引入松弛因子, 可以較好地維持上述平衡。在分別建立包含特征值(活動個數、候選服務個數、約束強度和約束個數)與標簽(松弛因子)的訓練集、神經網絡模型的基礎上, 提出了一種基于神經網絡的松弛因子自適應調節方法。仿真實驗分析表明, 該方法優于現有方法。由于工作流、時序約束位置的不確定性, 以及松弛因子的分類個數較多, 如何在NN訓練時避免或減少人工干預而保障較好的訓練精度, 仍值得關注。