裝配式鋼-混組合梁橋振動頻率的簡化計算

[摘? 要]：為確定裝配式鋼-混組合簡支梁橋的振動頻率的簡化計算方法，文章根據D′Alembert原理，以慣性力法推導了此類橋梁的豎向彎曲振動振動頻率計算公式和考慮剪切變形和轉動慣量的橫向振動頻率計算公式，并選取6座不同跨徑、不同主梁數和不同主梁高度的裝配式鋼-混組合簡支梁橋，分別采用推導公式、推薦公式、規范公式和ANSYS有限元分析軟件對其自振頻率進行了計算分析，分析結果表明：推導公式用于鋼-混組合簡支梁橋的振動頻率的計算，所得結果與有限元法計算結果吻合良好;式（10）～式（12）計算誤差較大，不宜用于鋼-混組合簡支梁橋的豎向彎曲振動頻率的計算;JTG D60-2015《公路橋涵設計通用規范》推薦的簡支梁橋的自振頻率計算公式可用于計算鋼-混組合簡支梁橋的自振頻率，且計算結果與有限元法所得結果吻合良好。所得結論可為同類型橋梁的自振頻率估算提供理論依據。

[關鍵詞]：橋梁工程; 自振頻率; 有限元法; 鋼-混組合梁; 裝配式; 能量法

U 448.21+6A

裝配式鋼-混組合梁橋以其施工周期短、裝配化程度高及全壽命周期經濟性好等優點，在現有橋梁中所占比例越來越大[1-2]。

對于裝配式鋼-混組合梁橋的靜力學性能方面的研究，國內外學者主要集中于荷載橫向分布系數計算[4-6]、抗彎承載力計算[7]及考慮混凝土和鋼材2種材料間相對滑移的撓度和剪力釘受力性能計算[8-9]。在動力學研究方面，國內外學者主要集中于振動特性的控制[10]、車-橋耦合動力沖擊[11]及車輛作用下疲勞特性的研究[12]。研究采用的方法大多為有限元法。

現有研究成果對于裝配式鋼-混組合梁橋的自振特性的研究較少?，F行規范中，對于鋼-混組合梁橋的自振頻率的計算也未明確給出計算公式，JTG D60-2015《公路橋涵設計通用規范》建議使用有限元法計算橋梁的自振頻率，且對于常規的預應力混凝土梁橋的自振頻率計算給出了估算公式。但時有限元模型的建立費時費力且對于計算結果的正確性較難把握，估算公式是否適用于裝配式鋼-混組合梁橋的自振頻率計算，尚未可知。因此，本文通過對裝配式簡支鋼-混組合梁橋的豎向自由振動頻率及橫向振動頻率計算公式進行了推導，并通過多參數變化的裝配式鋼-混組合梁橋算例，對比了本文推導公式和有限元法、集中折算質量法、能量法和規范估算公式的自振頻率計算結果進行了對比分析。所得結果可為同類橋梁的自振頻率的計算提供理論參考。

1 簡支鋼-混組合梁的豎向自由振動

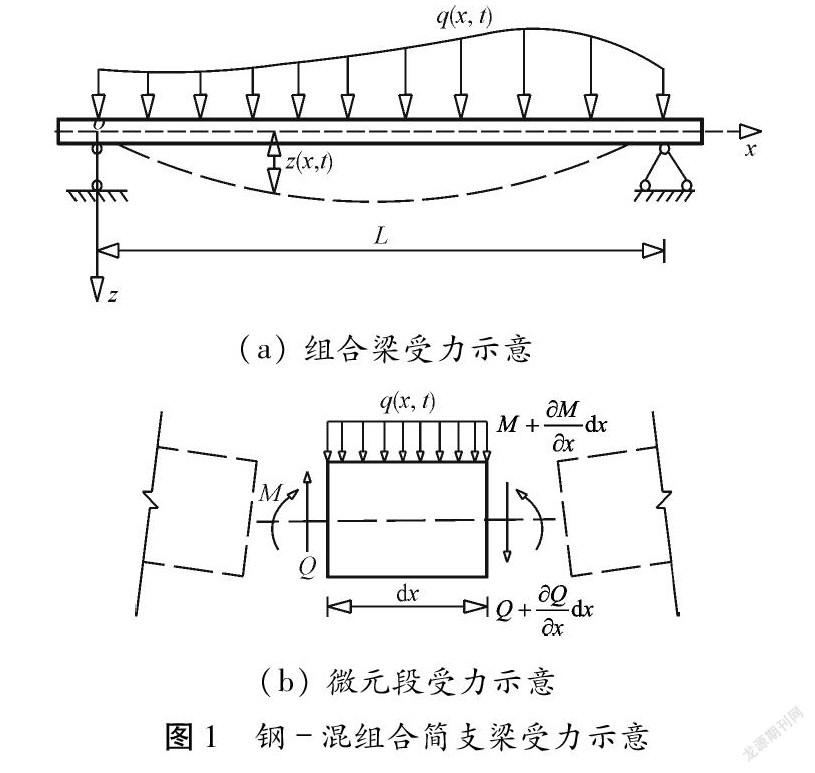
如圖1所示跨徑為L的鋼-混組合簡支梁橋，其沿跨徑方向的單位長度質量和抗彎剛度分別為m（x）和EsIcb（x），其上作用有隨x和時間t變化的橫向荷載q（x，t），荷載作用下梁截面在t時刻的撓度為z（x，t）。取梁段某長度為dx的微元段作為研究對象，分析簡支鋼-混組合梁的豎向彎曲振動特性。

依據初等變形理論，微元體受力如式（1）所示的關系。

M=EsIcb2zx，tx2

Q=Mx

qx，t=Qx（1）

根據D′Alembert原理，以慣性力法建立鋼-混組合簡支梁系統的運動方程如式（2）所示。

EsIcb4zx，tx4=m2zx，tt2（2）

根據分離變量法，引入位移函數Z（x）和時間函數T（t）并引入變量u2=m/EsIcb表示式（2），則有：

Z′xZx=-u2T··tTt（3）

欲使得式（3）成立，顯然，當左右兩邊關于不同變量參數的部分均為常數時，等式成立。因此為方便式（3）的求解，引入常數j4并令：

工程結構王乾波： 裝配式鋼-混組合梁橋振動頻率的簡化計算

Z′xZx=-u2T··（t）T（t）=j4（4）

Z（x）=esx（5）

將式（4）和式（5）代入式（3）關于位移的函數有：

esxs4-j4=0（6）

式（6）解的一般形式為：

Z（x）=Asin（jx）+Bcos（jx）+Csinh（jx）+Dcosh（jx）（7）

代入梁端邊界條件，易得系數A=B=C=0，則式（7）為Zx=Asinjx，顯然，為使式（7）有意義，A≠0，而根據簡支梁的邊界條件，當x=L時，sin（Lx）=0，因此則有：

j=rπL（8）

式中：r為鋼-混組合梁的自由振動階數，當r=1時，所求振動頻率即為結構的基頻。

求鋼-混組合簡支梁的豎向自由振動頻率計算公式為：

fr=ji22πu=r2π2L2EsIcbm（9）

對于簡支梁豎向自由振動頻率的計算，文獻[14]推薦了2種及近似計算方法，其分別為基于集中折算質量法的式（10）和基于能量法分別取撓度曲線和二次拋物線為第一階振型的式（11）和式（12），而JTG D60-2015《公路橋涵設計通用規范》提出，可使用式（13）來估算簡支梁橋的自振頻率。

f=9.8652πL2EIm（10）

f=9.872πL2EIm（11）

f=10.952πL2EIm（12）

f=π2L2EIm（13）

2 簡支鋼-混組合梁的橫向振動

前文對于簡支鋼-混組合梁的豎向振動的推導過程中，并未考慮梁截面在振動過程中的剪切變形和轉動慣量的影響，即是基于歐拉梁理論進行的推導。而對于高跨比較大的簡支鋼-混組合梁橋的自振頻率的計算，其剪切變形和轉動慣量的影響較大，一般不容忽略。因此，本節推導考慮剪切變形和轉動慣量的簡支鋼-混組合梁的橫向振動計算公式。簡支鋼-混組合梁的縱向受力與圖1一致，考慮剪切變形的微元體受力示意如圖2所示。

設截面轉角為φ，剪切角為β，則考慮轉動慣量和剪切變形的時，梁的軸線轉角如式（14）所示。

zx=β+φ（14）

依據小變形理論和力的平衡，并不計高階微量有：

Qx+qx，t-m2t2zx，t=0（15）

Mx-Q+ρsIcbx2φx，tt2=0（16）

式中：ρs為鋼材的密度。

根據初等梁的彎曲理論有：

Q=j′AeGeβ（17）

M=-EsIcbφ（x，t）x（18）

式中：j′為截面的有效剪切系數，Ae為組合梁換算截面面積，Ge為組合梁換算截面剪切彈性模量。

將式（14）、式（17）和式（18）分別代入式（15）和式（16）得：

m2z（x，t）t2-q（x，t）-xj′AeGezx-φ=0（19）

ρsIcbx2φx，tt2-j′AeGezx-φ-xEsIcb2φx，tt2（20）

式（20）對x求導有：

xρsIcb2φx，tt2-xj′AeGezx-φ

-2x2EsIcb2φx，tt2=0（21）

將式（19）代入式（21）并整理得考慮了轉動慣量和剪切變形的梁的橫向彎曲動力方程如式（22）所示。

ρsIcb4zx，tx2t2+ρsIcbj′AeGe-EsIcbj′AeGe2t2qx，t-m2zx，tt2

-qx，t-m2zx，tt2-EsIcb4zx，tx4=0（22）

假定振型函數和位移隨時間簡諧變化的模式為：

φx=CnsinnπxL（23）

zx，t=φxsinωt（24）

將式（23）、式（24）代入式（22），并令p4=f2m2πEsIcb，ρsIcb=mi2，整理得：

p4i2p4i2-Esj′Ge-1+Esj′GerπL2-p4+rπL4=0（25）

式中：i為慣性半徑，其值為Icb/Ae。

對式（25）求解，即可得到簡支鋼-混組合梁的橫向振動頻率計算公式：

f=rπL2EsIcbmrπL2i2+EsIcbj′AeGe+1（26）

3 算例

3.1 橋梁概況

為綜合驗證不同跨徑和截面特性的鋼-混組合梁橋的自振頻率，選取不同跨徑、主梁高和主梁數的鋼-混組合簡支梁橋作為研究對象[6]，對其在不同方法計算下的自振頻率計算值進行分析。鋼-混組合梁橋混凝土橋面板為C50混凝土，厚度為20.5 cm，彈性模量、泊松比和密度分別取26 GPa、0.25和2 400 kg/m3。鋼主梁頂、底板寬均為40 cm，頂、底板及腹板厚度分別為15 mm、25 mm和10 mm，鋼主梁為Q345c鋼板，彈性模量、泊松比和密度分別取200 GPa、0.3和7 850 kg/m3。橋梁參數如表1所示，橋梁縱、橫截面示意如圖3所示。

3.2 有限元模型的建立

采用有限元分析軟件ANSYS建立實體單元有限元模型，實體單元選用solid45單元。所建模型中，混凝土與鋼主梁共節點，不考慮兩種材料間的相對滑移。主梁下翼緣板底板節點處設置支承約束用以模擬支座作用。該建模方法已在文獻[4，6]中驗證了其正確性。所建立2號橋梁的有限元模型如圖4所示。

3.3 截面特性計算

組合截面梁截面計算時，應進行組合梁翼緣有效寬度計算[15]，文中組合梁截面的翼緣板有效寬度計算參考JTG D64-2015 《公路鋼結構橋梁設計規范》中的附錄F進行計算，通過計算知，文中的6座鋼-混組合截面橋梁的組合梁翼緣有效寬度為全截面利用。另外，11.1.3節第2條指出，對于剛-混組合截面進行截面特性計算時，宜采用換算截面法進行計算，即在保證截面換算前后組合截面形心高度不變的前提下，將混凝土橋面板換算成與鋼主梁相同材料的鋼材。截面換算示意如圖5所示。其中，hc為換算前截面的混凝土橋面板厚度，beff為翼緣板的有效寬度，bs為換算后鋼梁的翼緣板寬度，hs為換算后鋼翼緣板的厚度，zc和zs分別為鋼主梁底面到混凝土橋面板形心和鋼主梁形心的距離。

組合梁截面慣性矩計算公式如式（27）所示。

Icb=∑ni=1Icα+Is+AcAsαAs+Ac（zc-zs）2（27）

式中：Icb為組合梁截面慣性矩;n為主梁數;Ic為主梁混凝土橋面板的慣性矩;α為鋼材和混凝土彈性模量比;Is為但鋼主梁截面的慣性矩;Ac為混凝土橋面板截面面積;As為鋼主梁截面面積。

通過式（27）計算所得各橋梁的截面特性如表1所示。

4 振動頻率計算結果分析

采用ANSYS求解到1號橋的前四階振型如圖6所示。

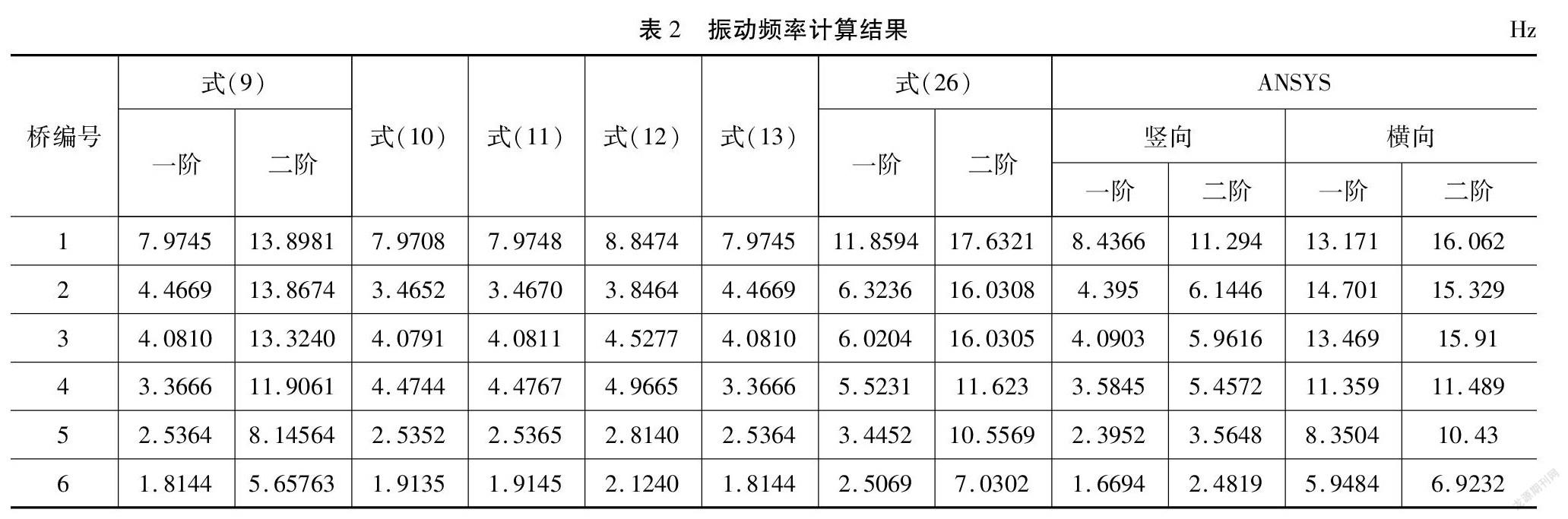
采用不同方法計算得到的各橋梁的振動頻率如表2所示。

從表2中可看出，對于一階豎向彎曲振動的頻率，采用式（9）和式（13）計算出的一階豎向彎曲振動頻率一致，其與ANSYS計算出的基頻的最大誤差為7.99%;式（10）～式（12）計算得到的豎向彎曲頻率與ANSYS計算的基頻的最大誤差分別任26.83%、26.77%和27.83%;式（9）計算得到的二階豎向彎曲頻率與ANSYS結算結果間最大誤差為6.01%;式（26）計算得到的一階、二階橫向彎曲振動頻率與ANSYS結算結果之間最大相差4.77%和8.90%。可見，本文推導的組合梁橋的頻率計算公式具有較好的精確性，但文獻[14]推薦的豎向彎曲振動頻率計算方法與有限元法計算結果之間誤差較大，JTG D60-2015《公路橋涵設計通用規范》推薦的豎向一階彎曲振動頻率計算公式有較高的精確度。

5 結論

（1）所推導組合梁橋的豎向和橫向振動頻率計算公式與ANSYS計算結果吻合良好，具有較好的計算精度，可作為同類型橋梁振動頻率的計算依據。

（2）式（10）～式（12）較有限元法計算誤差較大，不宜用于組合簡支梁橋的自振頻率計算。

（3）式（13）用于計算組合簡支梁橋的豎向彎曲振動基頻具有較高的計算精度。

參考文獻

[1] 劉永健， 高詣民， 周緒紅， 等. 中小跨徑鋼-混凝土組合梁橋技術經濟性分析[J]. 中國公路學報， 2017， 30（3）： 1-13.

[2] 田山坡. 鋼混組合梁剪力連接件的計算方法研究[J]. 鐵道工程學報， 2014， 31（8）： 56-61.

[3] 張翼， 李永樂， 汪斌， 等. 大跨度板桁加勁梁懸索橋自振頻率參數敏感性分析[J]. 中外公路， 2019， 39（3）： 125-128.

[4] 閆林君， 張經偉， 羅奎. 裝配式多主梁鋼-混組合梁橋的荷載橫向分布研究[J]. 公路交通科技， 2020， 37（3）： 59-69.

[5] 李瑞琪， 袁萬城， 高康， 等. 裝配式簡支鋼-混組合小箱梁橋荷載向分布系數的研究[J]. 結構工程師， 2015， 31（4）： 54-59.

[6] Kim Y J， Tanovic R， Wight R G. A parametric study and rating of steel I-girder bridges subjected to military load classification trucks[J]. Engineering Structures， 2013， 56（2013）： 709-720.

[7] 李立峰， 王孝亮， 馮威， 等. 考慮鋼梁應變強化的鋼-混組合梁抗彎承載力計算[J]. 鐵道科學與工程學報， 2019， 16（11）： 2822-2831.

[8] 冀偉， 孫斌， 鄧露， 等. 多因素影響下鋼-混連續組合梁的撓度計算分析[J]. 湖南大學學報（自然科學版）， 2019， 46（5）： 30-38.

[9] 項貽強， 郭樹海. 復雜應力條件下快速施工鋼-混組合梁群釘推出試件參數分析[J]. 中國公路學報， 2017， 30（3）： 246-254.

[10] 荊國強， 吳肖波， 王波， 等. 雙工字鋼一混組合連續梁橋振動特性與控制研究[J]. 橋梁建設， 2019， 49（S1）： 39-44.

[11] 喬朋， 鐘承星， 王宗義， 等.我國車-橋耦合振動的研究現狀及發展趨勢[J]. 重慶交通大學學報（自然科學版）， 2019， 38（12）： 26-37.

[12] 李巖， 楊婷婷， 商賀嵩， 等. 考慮多因素影響的裝配式梁橋橫向聯系疲勞損傷評估[J]. 湖南大學學報（自然科學版）， 2019， 46（9）： 79-88.

[13] 公路橋涵設計通用規范： JTG D60-2015[S]. 北京：人民交通出版社， 2015.

[14] 胡人禮. 橋梁力學[M]. 北京： 中國鐵道出版社， 1999： 841-864.

[15] 公路鋼結構橋梁設計規范： JTG D64-2015[S]. 北京：人民交通出版社， 2015.