考慮不確定性的供應鏈可靠性優化設計

閆 英 鎖 斌 何曉蘭

(1.西南科技大學經濟管理學院 四川綿陽 621010；2.西南科技大學信息工程學院 四川綿陽 621010)

隨著市場競爭日益加劇，目標客戶對產品響應時間的要求越來越高，而分工的精細化和專業化也使得供應鏈越來越復雜，更容易受到各種不確定性因素的干擾。供應鏈的抗沖擊、抗風險、穩定運作能力已成為供應鏈企業的核心競爭力之一。如何診斷、分析、設計并提高供應鏈的可靠性受到了國內外學者的廣泛關注[1-8]。

在工程可靠性領域，“可靠性是設計出來的”這一理念已得到廣泛認同，可靠性優化設計研究受到了高度重視[9-11]。同樣，對于供應鏈來說，其可靠性也依賴于系統規劃和設計階段供應鏈系統的構建和配置。目前國內在供應鏈可靠性優化設計方面做了一些初步探索。余小川等[12]研究了串并聯邏輯結構對物流系統可靠性的影響，并對有約束下的物流系統成本優化問題進行了初步探討；張德海等[13]研究了基于故障樹的物流服務供應鏈可靠性指標分配方法，并以汽車整車物流服務供應鏈為對象建立了服務能力優化模型；鄭哲文[14]采用模糊層次分析法研究了應急供應鏈系統的可靠性設計；陳德良等[15]研究了可靠性約束下的物流中心選址問題，并采用改進的遺傳算法求解。總的來說，目前國內在供應鏈可靠性優化設計方面的研究還很不成熟，尤其是以上研究均未考慮到供應商供應能力的不確定性和采購價格的不確定性。本文將在充分考慮這些不確定性因素的情況下研究制造商(核心企業)與供應商構成的兩級供應鏈的可靠性優化設計問題，構建更加實用的最優化模型，以期在滿足可靠性要求的前提下達到最優成本。

1 問題描述

本文研究由一個制造商(核心企業)和多個供應商組成的兩級供應鏈系統。設制造商需要采購m種類型的零配件，每種零配件都有Ni(i=1,2,…m)個供應商，第i種零配件的供應商記為Si1,Si2,…SiNi。若將供應鏈失效定義為頂事件，則當任何一種零配件的供應環節失效，則供應鏈失效，因此各個零配件供應環節之間為串聯關系；零配件i供應環節中有Ni個供應商共同為制造商供貨，單個供應商失效不一定會導致供應鏈失效，因此供應商之間為并聯關系。據此，可構造由制造商和多個供應商組成的兩級供應鏈模型，如圖1所示。

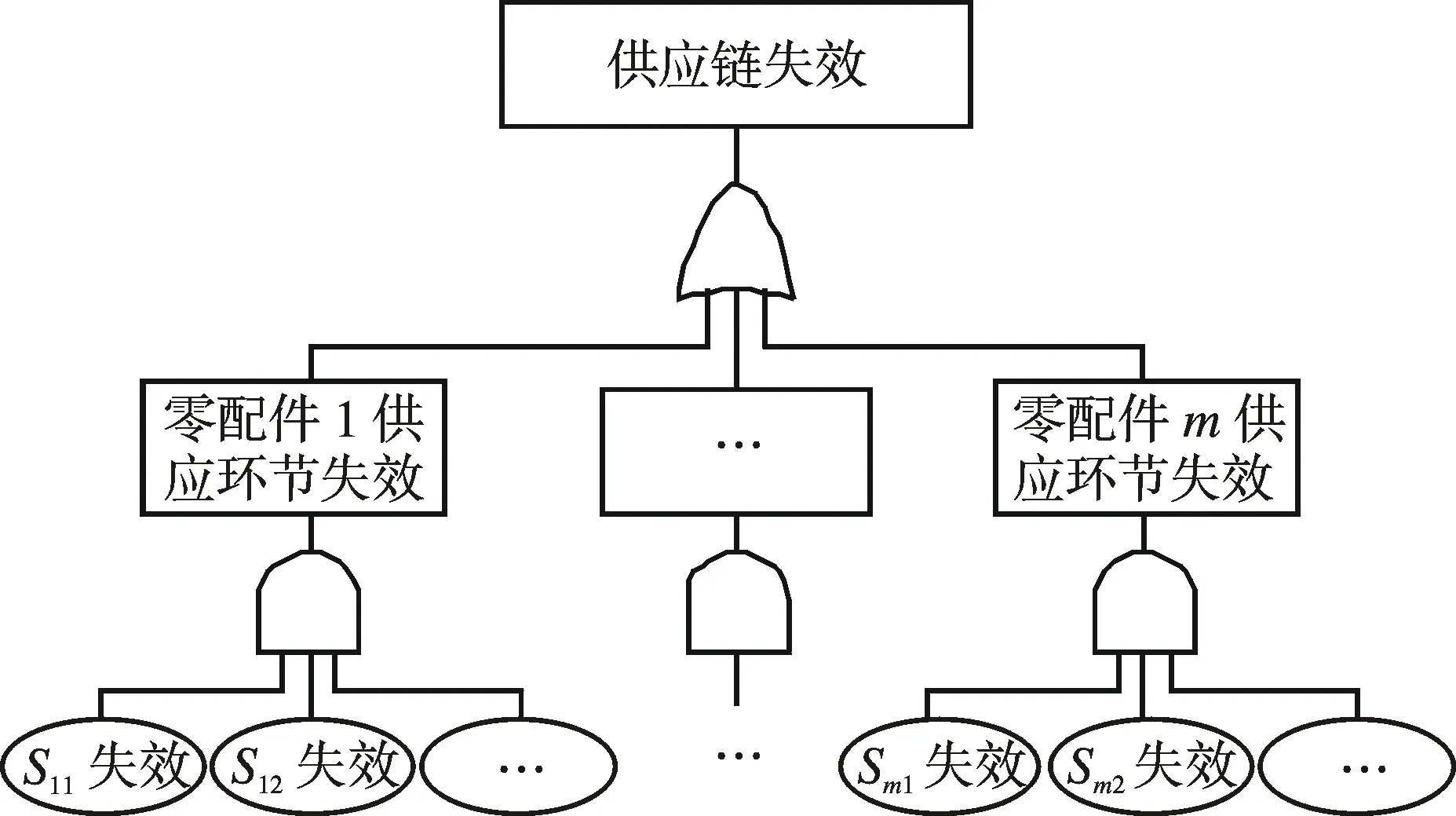
圖1 兩級供應鏈模型Fig.1 Two-level supply chain model

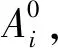
(1)

零配件i供應環節的可靠度為Ri，則整個供應鏈的可靠度為：

(2)

由圖1可知，供應商的數量Ni越大，可靠度R0越高；同時，由于單個供應商的采購數量下降，單價Pi必然會增加，總成本C也會增大。供應鏈由m個供應環節組成，每一個環節的可靠性都會影響到供應鏈整體可靠性。對于可靠度較低的單元供應商，通常需要提高并聯單元的數量來保證供應鏈整體可靠度，但同時也會增加成本。由式(2)可知，降低某些成本較高的供應環節的可靠性，同時增加其他成本較低環節的可靠性，同樣可以保證整個供應鏈的可靠性水平，而且可獲得更低的成本。因此，如何合理選擇供應商的數量，構建既滿足可靠性要求、又能達到最低成本的供應鏈，是一個值得研究的問題。

2 供應鏈可靠性優化設計

2.1 可靠性優化設計模型

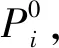
(3)

其中δi為常數，表示零配件i的單價修正參數。

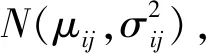
(4)

為便于討論，假設Ni個供應商的供應能力相同，則由(4)式可得：

(5)

由式(5)可知零配件i供應環節的可靠度Ri是Ni的函數。

在可靠度約束下，就需要優化供應鏈結構，確定各個供應環節最優的供應商數量N=(N1,N2,…Nm)，從而使供應鏈達到最低的成本。因此提出以下供應鏈可靠性優化設計模型：

(6)

2.2 可靠性優化設計模型求解

式(6)的最優化問題難以直接用解析的方法求解，因此采用以下數值仿真的方法來搜索最優解。

步驟1：設搜索次數初值L=1，初始供應商數量為N(1)=(N1,N2,…Nm)=(1,1,…1)，帶入式(2)-式(6)計算R(1)和C(1)。若R(1)≥R0，則N(1)即為最優供應商數量，C(1)即為最優成本，結束；否則轉步驟2。

步驟2：通過重要度分析確定需要增加供應商的環節k。一般來講，供應鏈的成本和可靠度都非常重要，成本是越低越好，可靠度則是越高越好，因此以第i個供應環節增加1個供應商后的可靠度增量與成本增量倒數的乘積作為該供應環節的綜合重要度系數：

(7)

其中，ΔRi表示可靠性重要度，且

(8)

ΔCi表示成本重要度，且

(9)

記

k=index(max(Ii|i=1,2,…m))

(10)

則第k個供應環節需要增加1個供應商，即Nk=Nk+1，L=L+1，轉步驟3。

步驟3：根據式(4)-式(6)計算R(L)和C(L)。若R(L)≥R0，則N(L)即為最優供應商數量，C(L)即為最優成本，結束；否則轉步驟2。

值得注意的是，在以上算法中，剛開始搜索時Ri(i=1,2,…m)和R可能很小(趨近于0)，由于計算機浮點數存儲精度的原因，Ri和R的計算結果會為0，當Ri首次大于0時，搜索算法會陷入局部最優，始終停留在第i個零配件供應商。為避免這一問題，設置一個門限值ε，按如下方法改進搜索算法：

if in(Ri)≤ε

k=index(min(Ri|i=1,2,…m))

else

k=index(max(Ii|i=1,2,…m))

end

Nk=Nk+1

ε可取(0,0.5)之間的值，可以很好避免陷入局部最優的問題，較快收斂到全局最優解。

3 實例分析

某制造商和5類零配件供應商構成的供應鏈，為了獲得更大的市場競爭優勢，需要在保證一定可靠度的前提下盡量節約成本。設制造商對5類零配件的月需求數量(單位：件)分別為800，400，500，900，300，單個供應商月采購數量分別低于300，200，200，500，200時的基本單價(單位：元/件)分別為50，60，40，70，130，單價修正參數(單位：元/件)分別為2，3，4，5，17，每類零配件有若干個供應商可選擇。受原材料采購和生產因素的影響，各類零配件供應商的供應能力服從正態分布，分布參數如表1所示。現需要確定5類零配件供應商的最優數量，從而使供應鏈滿足0.96的可靠度且成本最低。

表1 供應商供應能力的分布參數Table 1 Distribution parameters of supplier’s supply capacity

從初始數量(1,1,1,1,1)開始搜索，設門限值ε=0.01，當首次出現min(R1,R2,…R5)>ε時，供應商數量為(2,1,2,2,1)，此時綜合重要度系數為I=10-3×(0.0116 0.8258 0.0000 0.2125 0.0044)

因此k=2，需要在第2個零配件供應環節增加一個供應商，轉入下一步繼續搜索，直到R≥0.96為止。搜索過程中各零配件供應商數量的變化和可靠度如表2所示，經過8次搜索后得到最優解。最終的結果如表3所示。

表2 最優供應商數量搜索過程Table 2 Search process for the number of the optimal suppliers

若在搜索算法中僅以式(5)中的可靠性重要度為依據進行搜索，則得到的最優解如表4所示。

對比表3、表4可以看出，雖然兩種方法得出的最優解均可滿足供應鏈可靠性要求，但同時考慮可靠度與成本的綜合重要度系數搜索算法得出的供應鏈總成本明顯更低，因此供應商數量的設置更為合理。

表3 可靠性優化設計的最優解Table 3 Optimal solution of reliability optimization design

表4 僅考慮可靠性重要度時的最優解Table 4 The optimal solution only considering reliability importance

4 結論

本文針對制造商(核心企業)與供應商構成的兩級供應鏈在規劃設計時的可靠性優化設計問題，提出了供應鏈最優化模型。該模型充分考慮了供應鏈各個環節供應商的不確定性和市場價格的不確定性，更加貼近實際情況。在模型的求解中，提出了同時考慮供應鏈可靠性和成本的綜合重要度系數及搜索算法。實例分析表明，本文提出的方法能夠在滿足可靠性要求的前提下有效確定供應鏈中各個環節供應商的最優數量，從而使供應鏈總成本最低。該方法可為核心企業在供應鏈設計階段優化供應商數量提供理論依據。另外，雖然本文研究的對象是制造商-供應商組成的兩級供應鏈，但對于多級供應鏈的可靠性優化設計，本文提出的方法同樣適用。