基于SSA-BP的離港航班滑出時間預測

黃龍楊， 夏正洪， 賈鑫磊

(中國民用航空飛行學院空中交通管理學院， 廣漢 618307)

滑出時間是指離港航班從停機位推出開車并滑行至跑道上實際起飛的時間間隔，它是評估繁忙機場場面運行效率的主要性能指標[1]。隨著機場跑滑系統結構及其運行模式日益復雜，大型樞紐機場的離港航班平均滑出時間已高達25 min。目前，多數機場采用基于經驗的滑出時間來對離港航班進行管制指揮，而實際滑出時間與經驗滑出時間往往相差甚遠，航班的過早推出或不恰當的滑出時機都將導致出現不必要的擁堵、延誤和燃油消耗，并且將嚴重影響機場場面運行效率。因此，科學準確地預測離港航班的滑出時間，對于提升機場場面運行效率和協調決策能力，降低運行成本和污染排放至關重要。

國外的離港航班滑出時間相關研究成果主要集中在對其影響因素和預測方法的研究。其中，影響因素主要包括離港隊列長度、滑行距離、地面交通流情況、跑道運行模式、天氣狀況、流控情況等；研究方法集中于排隊論[1]、機器學習[2]、強化學習[3- 4]等。中國關于離港航班滑出時間預測的研究還處于起步階段，劉繼新等[5]分析了離港航班滑出時間的影響因素。馮霞等[6-7]基于排隊論和支持向量回歸(support vector regression, SVR)方法對單跑道機場的離港航班滑出時間進行了預測，但是所得預測結果精度僅為75%左右。邢志偉等[8]基于貝葉斯網絡和LWSVR方法對滑出時間進行了預測方法，預測精度提升至85%左右[9]。Lian等[10-11]利用支持向量機預測離港航班的滑出時間，并基于滑出時間進行了推出策略的控制。Li等[12]基于深度學習方法對單跑道機場離港航班的滑出時間進行了預測。可見，現有研究成果主要以單跑道或者多條跑道中的一條跑道為研究對象，且預測結果的精度還需要進一步的提升。同時，基于支持向量機(support vector machine, SVM)和反向傳播(back propagation, BP)神經網絡的離港航班滑出時間預測結果對初始權值和閾值較為敏感、準確性和穩定性表現不佳。

為此，提出了一種基于麻雀搜索算法獲取BP神經網絡的最優權值和閾值的方法。首先分析了離港航班滑出時間的可量化影響因素及相關性，基于相關性分析結論構建了基于BP神經網絡的離港航班滑出時間預測模型，創新性地使用麻雀搜索算法對BP神經網絡的初始權重和閾值進行優化，并采用我國中南某樞紐機場2周的實際運行數據對預測模型進行了驗證。以期通過對離港航班滑出時間科學準確的預測，優化其推出開車時刻和起飛時刻，從而提升機場場面運行效率，減少燃油消耗和污染排放。

1 滑出時間影響因素及相關性分析

1.1 影響因素

離港航班滑出時間(taxi out time, TOT)等于該航班離港實際起飛時間(actual take off time, ATOT)與實際撤輪檔時間(actual off block time, AOBT)之間的差值，即

TOT=ATOT-AOBT

(1)

離港航班的滑出時間可以分為場面滑行時間和跑道外排隊等待的時間兩部分。其中，場面滑行時間主要與場面交通流的大小有關，同時還與滑行距離的長短、轉彎個數、機組習慣、天氣等因素相關；同時段滑行的離港航班、進港航班數量越多，場面滑行時間可能越長，滑行距離越長則滑出時間也會相應的增長。跑道外排隊等待的時間主要與進港流量大小、航空器間隔配備、流量控制以及天氣等因素的影響。鑒于流量控制、機組習慣、天氣等因素不可量化，故僅考慮可量化因素對離港航班滑出時間的影響，主要包括同時段滑行的離港航班數量、同時段滑行的進港航班數量、同時段推出的離港航班數量、半小時平均滑出時間、滑行距離、轉彎個數等。

1.2 參數定義

(1)同時段滑行的離港航班數量x1，單位：架次。離港航班i可能與同時段滑行的離港航班j爭奪跑道和滑行道資源，兩者可能因滑行沖突導致滑出時間的增長。

(2)

式(2)表示航班j的實際起飛時間tATOT(j)剛好落在航班i的實際推出開車時間tAOBT(i)和實際起飛時間tATOT(i)之間的離港航班數量num(j)之和。

(2)同時段滑行的進港航班數量x2，單位：架次。離港航班i可能與同時段滑行的進港航班j爭奪跑道和滑行道資源，由于進港航班優先級通常高于離港航班，因此可能因滑行沖突導致離港航班滑行時間的增長。

(3)

式(3)表示航班j的實際落地時間tALDT(j)剛好落在航班i的實際推出開車時間tAOBT(i)和實際起飛時間tATOT(i)之間的進港航班數量num(j)之和。

(3)同時段推出的離港航班數量x3，單位：架次。離港航班i可能與同時段推出的離港航班j爭奪機坪和滑行道資源，可能因避讓沖突而導致滑行時間的增長。

(4)

式(4)表示航班i的實際推出開車時間tAOBT(i)剛好落在航班j的實際推出開車時間tTOBT(j)和實際起飛時間tATOT(j)之間的離港航班數量num(j)之和。

(4)以30 min為時間片的平均滑出時間x4，單位：s。機場地面交通流呈現典型的時變特征，在離港早高峰、晚高峰以及進港高峰等典型繁忙時段，離港滑出時間會顯著增加。目前，大型樞紐機場的離港航班平均滑出時間約為20 min，因此30 min平均滑出時間是衡量機場地面交通流狀況的重要指標。

(5)

式(5)中：ti為在某個30 min時間片內的第i架離港航班的實際滑出時間；n為該30 min時間片的離港航班總數。

(5)離港航班滑行距離x5，單位：m。大型樞紐機場往往存在多個停機坪區域，離港航班滑出時間與其所在停機位的物理位置關系甚為緊密，滑行距離越長，則該停機位滑出的暢通滑行時間越長。

(6)轉彎個數x6，單位：個。航空器直線滑行速度與轉彎滑行速度有較大的差異，因此離港航空器在滑出過程中經過的轉彎個數越多，則其滑行時間就會增加。根據停機位的位置和跑道滑行道運行模式，可獲得離港航班的滑行路線，即可求得轉彎個數。

1.3 相關性分析

所用數據來源于中南某樞紐機場2019年5月26日—6月8日的實際運行數據，數據集共有記錄12 323條，包含離港航班5 747架次和進港航班6 576架次；每條記錄由飛機呼號、機型、實際起飛時間、實際撤輪檔時間、實際落地時間、跑道號、停機位等關鍵信息組成。通過對數據整理，刪除重復及異常數據，并根據式(1)～式(5)依次得到同時段滑行的離港航班數量，同時段滑行的進港航班數量，同時段推出的離港航班數量，30 min平均滑出時間，滑行距離，以及實際滑出時間。最終得到樣本數據5 200條，如表1所示。

基于SPSS軟件對表1中的數據進行相關性分析，得到離港航班滑出時間影響因素的相關性分析結果如表2所示。

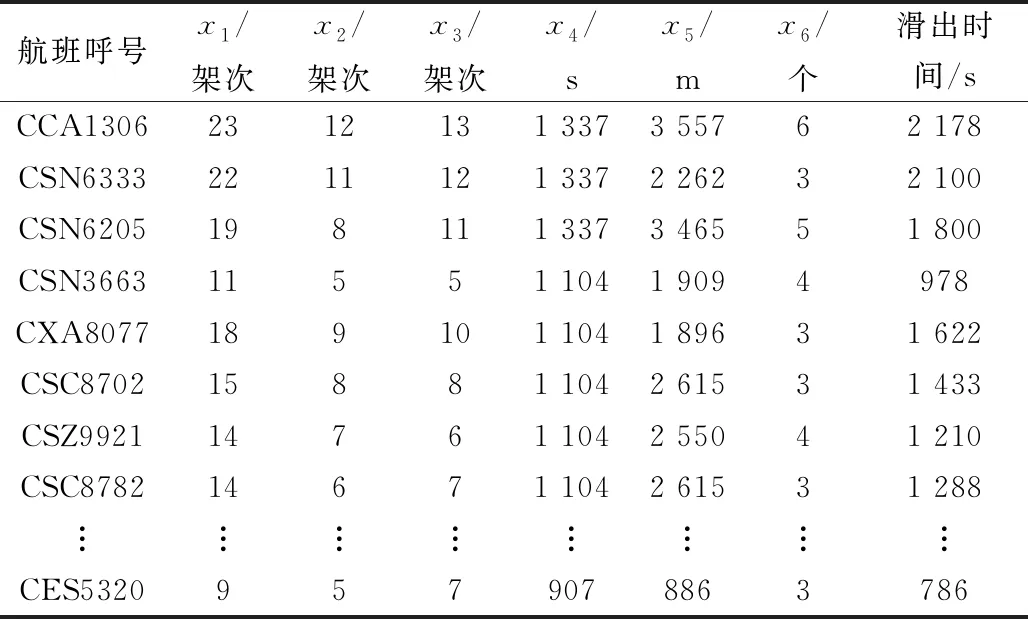
表1 樣本數據

表2 相關性分析結果

可見，離港航班滑出時間與同時段滑行的離港航班數量強相關(r>0.7)，與同時段滑行的進港航班、同時段推出的離港航班、半小時平均滑出時間均是中度相關(0.3

1.4 模型構建

根據離港航班滑出時間影響因素相關性分析結論，選取強相關性和中度相關性的影響因素，構建基于BP神經網絡的離港滑出時間預測模型如圖1所示。其中，網絡輸入節點數為4，包括同時段滑行的離港航班數量x1，同時段滑行的進港航班數量x2，同時段推出的離港航班數量x3，以半小時為時間片的平均滑出時間x4，輸出節點數為1。隱層節點數可根據輸入節點和輸出節點數先設置一個初始值，然后在此基礎上逐漸增加，比較網絡預測性能并選擇性能最好對應的節點數作為隱含層神經元節點數，最終確定為7。

圖1 基于BP神經網絡的離港航班滑出時間預測模型

2 基于SSA-BP的滑出時間預測模型

2.1 SSA算法

麻雀搜索算法是一種群體智能優化算法[13]，目前已逐漸應用于故障診斷[14]、航跡規劃等研究領域。它是一種基于麻雀的覓食行為和反捕食行為的群體優化算法，基本原理為：①發現者通常有較高的能量儲備，負責搜索到具有豐富食物的區域，為加入者提供覓食的區域和方向；②一旦麻雀發現了捕食者，發出鳴叫作為報警信號，當報警值大于安全值時，發現者將加入者帶到其他安全區域覓食；③發現者和加入者身份動態變化，但是各自所占種群數量的比重不變；④加入者的能量越低，則其所處的覓食位置就越差；⑤覓食過程中，加入者總能搜索到提供最好食物的發現者，并在其周圍覓食；⑥當意識到危險時，群體邊緣的麻雀會迅速向安全區域移動，以獲得更好的位置，位于種群中間的麻雀則會隨機走動，以靠近其他麻雀。其算法流程如下。

Step1初始化種群，迭代次數，初始化捕食者和加入者的比例。

Step2種群排序，得到當前的最優麻雀個體位置，以及最佳適應度值。

Step3覓食行為，按照式(6)更新發現者的位置。

Step4擴大覓食范圍，按照式(7)更新加入者的位置。

Step5縮小覓食范圍，按照式(8)更新警戒者的位置。

Step6反捕食行為，計算適應度值，更新麻雀種群位置，并更新最優適應度值。

Step7如滿足停止條件則輸出結果并退出，否則重復執行Step 2～Step 6。

發現者的位置更新規則為

(6)

式(6)中：Xi,j為第i個麻雀在第j維中的位置信息；t為當前迭代數；j=1,2,…,d，d為待優化問題的維數；α∈(0,1]為一個隨機數；itermax為最大迭代次數；Q為正態分布的隨機數；L為一個全1的行向量；R2和ST分別為警戒值和安全值，當R2

加入者的位置更新可表示為

(7)

警戒者的位置更新為

(8)

2.2 SSA-BP預測模型

針對傳統BP神經網絡在離港航班滑出時間預測時存在對初始權值和閾值敏感、準確性和穩定性不好等缺點，利用麻雀搜索算法的覓食和反捕食行為不斷更新種群的適應度和最優位置，從而獲取BP神經網絡的最優權值和閾值參數，然后再進行訓練和仿真預測，其算法流程圖如圖2所示。

圖2 基于SSA-BP的滑出時間預測流程圖

選用麻雀搜索算法優化BP神經網絡的初始權重和閾值。選取訓練集與測試集整體的均方誤差作為適應度。適應度函數越小，表示訓練越準確，且兼顧模型的預測精度更好。首先從Excel中讀取樣本數據，確定網絡的輸入輸出，劃分訓練集和測試集并將數據進行歸一化處理；然后確定網絡的拓撲結構，隨機初始化網絡的權值、閾值，麻雀種群規模、最大迭代次數、捕食者和發現者的比例等參數，以均方誤差最小值作為最優適應度，將優化后麻雀位置信息作為權值與閾值賦給BP，并對SSA優化后的BP神經網絡進行訓練與仿真預測。

3 滑出時間預測結果分析

基于MATLAB中的神經網絡工具箱進行編程，設置BP神經網絡最大迭代次數10 000次，學習率為0.001，目標收斂誤差為0.001；麻雀初始種群大小為50，最大迭代次數60，發現者和加入者占種群的比重均為0.5，能意識到有危險的麻雀占種群的比重為0.2。將樣本數據集中隨機抽取5 000個數據進行訓練，則剩余的200個數據作為測試集，經SSA優化前后的BP神經網絡預測值與真實值的對比[圖3(a)]，以及優化前后的誤差對比[圖3(b)]。

圖3 SSA-BP與BP預測結果及誤差對比

BP與SSA-BP兩種預測模型均能實現對離港航班滑出時間的有效預測。基于SSA優化后的BP神經網絡預測結果更接近于真實值，且誤差分布更集中、更均勻。同時，從表3可以看出，基于SSA優化后的BP神經網絡預測結果誤差在±60 s內的準確率提升了20%，誤差±180 s內的準確率提升了12%，誤差±300 s內的準確率提升了7%。可見，所構建的模型輸出結果比現有研究成果的預測精度高，從而驗證了基于SSA-BP的離港航班滑出時間預測模型的有效性。但是，BP神經網絡訓練的效率一直以來都是神經網絡的一個弊端，單獨采用BP神經網絡對這5 000個樣本進行訓練和200個樣本預測所需時間約為35 s，而基于SSA優化后的BP神經網絡訓練和預測所需時間約為238 s。因此，精度的提升是以訓練效率的降低為前提的。

表3 滑出時間預測結果誤差分布對比

為進一步對基于SSA優化后的BP神經網絡預測結果進行科學評價，以平均絕對誤差百分比(mean absolute percentage error, MAPE)、平均絕對誤差(mean absolute error, MAE)、均方根誤差(root mean square error, RMSE)來進行驗證，結果如表4所示。

表4 離港航班滑出時間預測精度評價

可見，基于SSA優化后的BP神經網絡預測結果較優化前的MAPE提升了2.61%，MAE減少了11.73 s，RMSE減少了61.03 s。以上數據充分證明了所構建的基于SSA-BP的離港航班滑出時間預測模型和方法是合理的。

4 結論

(1)提出了一種基于麻雀搜索算法獲取BP神經網絡的最優權值和閾值的方法，并應用于離港航班滑出時間預測模型。

(2)離港航班滑出時間與同時段滑行的離港航班數量強相關，與同時段滑行的進港航班數量、同時段推出的離港航班數量、平均滑出時間中度相關，與滑行距離和轉彎個數弱相關。

(3)基于SSA優化后的BP神經網絡預測結果準確率有顯著提升，MAPE提升了2.61%，MAE減少了11.73 s，RMSE減少了61.03 s。

(4)下一步的工作重點將放在基于滑出時間預測的離港航班推出及滑行控制策略研究方面。