基于代價敏感學習的半監督軟件缺陷預測方法

張金傳 張 震

1(扎蘭屯職業學院 內蒙古 呼倫貝爾 162650) 2(中南大學計算機學院 湖南 長沙 410000)

0 引 言

軟件缺陷預測技術利用機器學習方法分析軟件缺陷歷史數據，標記出容易出現缺陷的軟件模塊。開發人員可以根據軟件缺陷預測結果合理地調度資源，提高軟件驗證效率，從而保障軟件質量[1]。由于大部分軟件缺陷集中在少數模塊當中，軟件缺陷數據的分布具有不平衡性[2-3]。此外，將無缺陷軟件模塊錯誤標記為有缺陷造成的代價遠小于將有缺陷模塊錯誤標記為無缺陷造成的代價。前者會造成測試資源的浪費，而后者會嚴重影響軟件的可靠性[4]。傳統的機器學習方法以最大化模型準確率為目標，假設數據分布平衡且不同類別的誤分類代價相等，在軟件缺陷預測中效果有限。針對這個問題，現有的研究通常基于代價敏感學習方法構建軟件缺陷預測模型，為少數類樣本與多數類樣本設置不同的誤分類代價。這些方法包括在數據層面上對有缺陷模塊的過采樣方法[5-7]、對無缺陷模塊的降采樣方法[8-10]，以及在算法層面上擴展樸素貝葉斯、神經網絡等傳統機器學習方法得到的代價敏感學習方法[3,11-12]。

目前的軟件缺陷預測方法均依賴于主觀輸入的誤分類代價，或者由訓練數據的分布得到相對合理的誤分類代價。然而，訓練數據往往只占整個數據集的小部分，訓練數據的分布不能反映真實的數據類別分布，僅僅通過訓練數據分布判斷模型參數具有很大的局限性。因此，本文在NB(Naive Bayes)和EM(Expectation Maximization)方法的基礎上展開，提出一種充分利用未標記數據的代價敏感學習方法——CSNB-EM。CSNB-EM方法在軟件缺陷預測中的優勢包括：(1) 方法為有缺陷軟件模塊與無缺陷軟件模塊設置合理的誤分類代價，基于代價敏感學習提高對有缺陷軟件模塊的識別能力；(2) 方法利用未標記數據迭代優化誤分類代價等模型參數，建立的軟件缺陷預測模型更加符合整個數據集的分布。在公開的MDP軟件缺陷數據集上進行的對比實驗表明，CSNB-EM方法在處理軟件缺陷數據時，預測性能明顯優于CS-NB、CS-NN等現有的代價敏感學習方法。

1 不平衡缺陷數據學習方法

軟件缺陷數據是一種典型的不平衡數據，有缺陷軟件模塊的數量遠遠小于無缺陷模塊。例如，美國航空航天局的MDP數據集[13]中，MC1項目的缺陷率為10.23%，PC1項目的缺陷率為8.04%。用追求高準確率的傳統機器學習方法處理缺陷數據時，很多有缺陷模塊會被判定為無缺陷。代價敏感軟件缺陷預測方法通過為不同類別設置不同的誤分類代價解決缺陷數據的不平衡問題，包括數據和算法兩個層面的方法。

數據層面的代價敏感方法大多采用重采樣技術，包括增加少數類樣本的過采樣方法和減少多數類樣本的降采樣方法。針對少數類樣本的過采樣方法隨機生成一定數量的有缺陷樣本并添加到數據集中，使得數據集中有缺陷樣本與無缺陷樣本的數量達到平衡[5-7]。例如，文獻[6]結合過采樣與Boosting技術提出PCBoost方法，在每一輪訓練開始時合成一定數量的少數類樣本，并把合成樣本加入到訓練數據集當中。為了防止部分不合理的合成樣本降低模型性能，方法在每一輪訓練結束時，刪除被誤分的少數類樣本。針對多數類樣本的降采樣方法通過減少無缺陷樣本的數量平衡數據集的類別[8-10]。文獻[9]提出了有效的降采樣方法：將多數類樣本分成多個子集，每個子集都和少數類一起訓練一個分類器，最后集成這些分類器。

文獻[14]指出，與數據層面的代價敏感學習方法相比，算法層面的代價敏感學習方法在處理不平衡數據時通常具有更好的性能。算法層面的代價敏感學習方法不改變數據分布，而是讓算法對誤分類代價較高的類別產生偏置[3,11-12]。例如，文獻[12]用不同的誤分類代價拓展決策樹算法來提高對少數類的識別能力，基于不同的特征子集訓練多個弱分類器并且集成弱分類器的預測結果。

代價敏感學習方法能有效提高模型對少數類的識別能力。基于代價敏感學習方法構建缺陷預測模型能顯著提高軟件缺陷預測的效果。然而，這些方法通常需要人為確定一組誤分類代價。在軟件缺陷預測的任務中，標記軟件模塊的成本高昂，有標記的訓練樣本通常遠少于無標記樣本。在這種情況下，難以基于訓練樣本得到適應整個數據集的誤分類代價。本文提出的CSNB-EM方法充分利用無標記樣本優化誤分類代價及其他模型參數，所建立的模型在軟件缺陷預測中具有明顯優勢。

2 軟件缺陷預測算法CSNB-EM

CSNB-EM方法首先在訓練數據集上構建樸素貝葉斯分類模型，應用交叉驗證搜索適合訓練數據集與該分類模型的最優誤分類代價，并將搜索到的誤分類代價應用在分類模型上，然后通過EM算法利用未標記數據集修正模型參數。

2.1 基于代價敏感的樸素貝葉斯方法

樸素貝葉斯方法是一種建立軟件缺陷預測模型的常用方法[15-16]。令L={(x1,y1),(x2,y2),…,(xn,yn)}表示訓練數據集合。對于任意0≤i≤n,yi表示樣本xi的類別。U={xn+1,xn+2,…,xn+m}表示一組未標記數據。數據集中的樣本有k個屬性，用aj表示第j個屬性，用aij表示樣本xi的第j個屬性，則xi={xi1,xi2,…,xik}。給定一個類別c，P(c|xi)表示樣本xi的類別為c的概率，P(xi|c)表示類別c中，樣本xi出現的概率，P(c)表示類別c出現的概率。根據貝葉斯理論，P(c|xi)可以通過P(c)·P(xi|c)估計。

P(c|xi)∝P(c)·P(xi|c)

(1)

在軟件缺陷預測的任務中，通常可以基于樸素貝葉斯方法假設數據的每個屬性獨立分布。樸素貝葉斯方法在軟件缺陷預測中的應用表明：該假設能顯著提高訓練模型的效率，而不會明顯降低模型性能[15-16]。基于該假設，式(1)可以寫為：

(2)

在處理不平衡數據時，基于式(2)標記樣本類別可能會降低少數類別樣本分類的準確率。針對這個問題，本文基于混淆矩陣引入不同的誤分類代價。設正例樣本為有缺陷樣本，類別用1表示，負例樣本表示無缺陷樣本，類別用0表示。對于任意1≤i≤n+m，都有ci∈C={0,1}。誤分類代價如表1所示。

表1 誤分類代價矩陣

基于誤分類代價矩陣，可以定義代價函數為:

(3)

本文通過最小化代價函數標記樣本的類別。為了簡化模型，令F(1,1)=F(0,0)=0。令F(1,1)>F(0,0)以提高負例樣本的分類準確率。當ci≠cj時，將F(ci,cj)簡寫為Fci。

2.2 調整模型參數

CSNB-EM算法基于未標記數據調整模型參數。具體做法為：基于模型參數建立模型，預測無標記樣本集的標記，然后利用這些標記修正模型參數。這個過程迭代進行直到模型參數與樣本標記收斂。

算法首先在訓練數據集上學習一組分類參數，包括P(c)與P(aj|c)。參數P(c)反映了數據類別的分布，P(aj|c)是樣本第j個屬性的條件概率。基于訓練數據集中樣本的類別可以計算得出P(c)與P(aj|c)。

(4)

(5)

式中：對于任意α與β，如果α=β，則φ(α,β)=1，否則，φ(α,β)=0。

首先令F(1,0)=F(0,1)=1，然后迭代進行E-step與M-step兩個步驟調整樣本類別與模型參數。

E-step:標記數據集U中的樣本。

f(xi)=argmincL(x,c)

(6)

M-step:調整模型參數。由于數據集U中樣本的標記未知，為這些樣本分配一個權重0<λ<1來降低無標記樣本對模型參數的影響。

(7)

(8)

Fc=argmaxFP(L,U,Z|hc,a|c,F)

(9)

式中：Z={f(xn+1),f(xn+2),…,f(xn+m)}表示對無標記樣本類別的預測結果；hc,a|c是P(c)與P(a|c)兩個模型參數。式(9)尋找的是適合當前步驟中的模型參數與樣本類別的誤分類代價。

CSNB-EM算法過程如算法1所示。

算法1CSNB-EM算法

輸入：最大迭代次數T，L={(x1,y1),(x2,y2),…,(xn,yn)},U={xn+1,xn+2,…,xn+m}。

輸出：U中樣本的標簽。

1.F0(1,0)=F1(0,1)=1;

2.根據式(4)與式(5)計算P0(c)與P0(a|c);

3.fort=1 toTdo

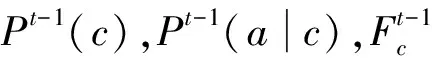
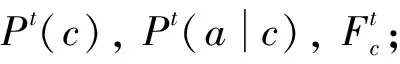
6.returnfT(x)

算法在第2步用樸素貝葉斯方法在訓練數據集上計算初始模型參數。第4步與第5步迭代利用模型參數標記數據類別，并利用數據類別修正模型參數，其中第4步對應E-step，第5步對應M-step。

2.3 估計誤分類代價

CSNB-EM算法根據訓練數據集、無標記數據集、無標記數據集的預測結果計算誤分類代價。本節給出誤分類代價最優取值的估計方法。方法基于不同誤分類代價對應的模型性能確定誤分類代價的取值。由于L與U中樣本的權重不同，在估計模型性能時，需要弱化U中樣本的影響，因此本文提出表2所示的加權混淆矩陣估計模型性能。

表2 加權混淆矩陣

表2中，TP表示被正確標記的有缺陷樣本的權重之和，FN表示被錯誤標記的有缺陷樣本的權重之和，TN表示被正確標記的無缺陷樣本的權重之和，FP表示被錯誤標記的無缺陷樣本的權重之和。其中：wi表示樣本xi的權重，如果xi∈L，wi=1，否則wi=λ；yi是樣本xi的標簽，如果xi∈U，則yi=f(xi)；h(xi)是模型預測的xi的類別。

由于缺陷數據的不平衡性，不能僅僅通過準確率評價模型性能。考慮到性能良好的模型即應該識別出多的正例，又要保證預測的準確性，通過以下兩項指標考察模型性能：

Recall=TP/(TP+FN)

(10)

Precision=TP/(TP+FP)

(11)

式中：Recall表示正例樣本中被預測正確的樣本所占比例；Precision表示被預測為正例的樣本中被預測正確的樣本比例。顯然，Recall的值高說明分類器對正例有較高的偏置，但對正例偏置過高會導致Precision的降低。合理的誤分類代價應該能使得模型在Recall與Precision兩個指標上達到一個最優折衷，參考文獻[17]，本文取Recall與Precision的幾何平均值作為衡量模型性能的標準。

(12)

本文在誤分類代價的范圍內迭代取值，構造模型并在數據集上進行10折交叉驗證，找到使得GeoM達到最大值的誤分類代價。為了計算方便，令F(1,0)=1，F(0,1)在(0,1)區間迭代取值。搜索誤分類代價的算法如算法2所示。

算法2搜索誤分類代價算法

輸入：代價增量ΔF，L={(x1,y1),(x2,y2),…,(xn,yn)}，Z={f(xn+1),f(xn+2),…,f(xn+m)},U={xn+1,xn+2,…,xn+m}，模型參數P(c)、P(a|c)。

輸出：誤分類代價F(0,1)。

1.F′=F*=1,Gmax=0;

2.whileF′>0do

3.根據模型參數F(1,0)=1,F(0,1)=F′，P(c)，P(a|c)與式(3)計算代價函數L(x,c);

4.通過最小化代價函數L(x,c)標記L∪U中樣本，得到h(x);

5.根據h(x)與式(12)計算GeoM；

6.ifGeoM>Gmaxdo

7.F*=F′,Gmax=GeoM;

8.F′=F′-ΔF;

9.returnF(0,1)=F*

算法根據訓練數據集合L、無標記數據集合U、U中樣本的預測標簽集合Z搜索誤分類代價的合理取值。通過加權混淆矩陣計算模型的GeoM指標，并返回使該指標最大化的誤分類代價取值。

3 實驗分析

3.1 數據集

本文采用NASA公開的MDP軟件缺陷數據集作為實驗數據，如表3所示。數據集可以從PROMISE網站上獲取[13]。數據集中的每個數據資源都表示一個NASA軟件項目內的模塊信息。表4中給出了數據集屬性的描述。由于數據屬性是連續的，本文使用基于MDL的離散化方法[18]將屬性離散化。

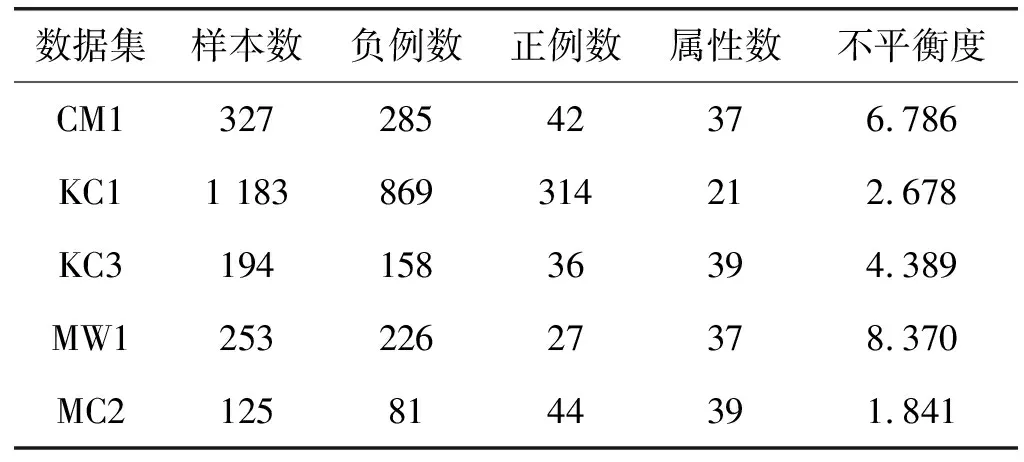
表3 數據集

表4 數據集屬性

3.2 與代價敏感方法的對比實驗

實驗選用GeoM與AUC作為算法的評價標準。GeoM表示模型Recall與Precision的幾何平均。AUC是ROC曲線下的面積，被認為是一種評價不平衡數據分類效果的優秀指標。高的AUC值對應理想的分類模型。實驗在MDP數據集上隨機抽取20%的樣本作為訓練數據，建立多個模型進行比較，包括：用代價敏感拓展樸素貝葉斯方法得到的CS-NB(Cost-Sensitive Naive Bayes)方法；代價敏感軟件缺陷預測方法CS-NN(Cost-Sensitive Neural Network)[11]。為了考察CSNB-EM方法自適應搜索最優誤分類代價的效果，首先在誤分類代價的范圍內動態調整誤分類代價構建CS-NB模型，通過在數據集上驗證模型效果找到最優誤分代價并在每個數據集上都用最優誤分類代價構建CS-NB模型與CSNB-EM方法對比。取F(1,0)=1，調整F(0,1)的取值。圖1是CS-NB方法在各個數據集上的GeoM值，表5是根據圖1為CS-NB方法搜索到的最優誤分類代價。

圖1 CS-NB模型性能比較

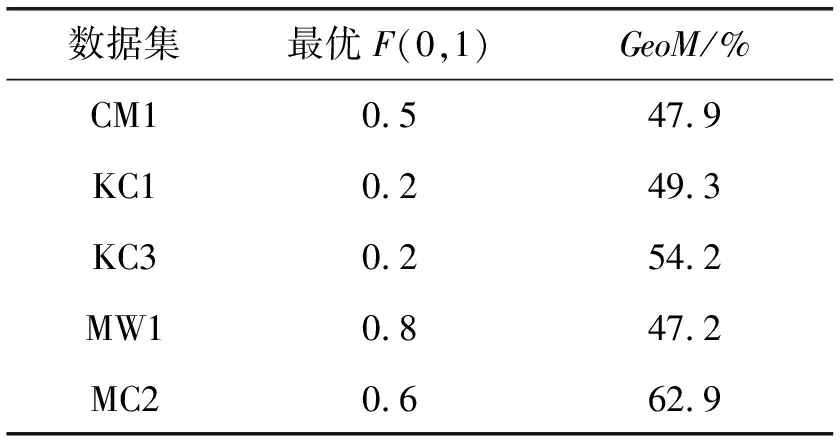
表5 CS-NB模型最優誤分類代價

可以看出，誤分類代價的選擇對CS-NB模型的GeoM值有明顯影響，不合理的誤分類代價與最優誤分類代價構造的模型在GeoM指標上相差很大。這說明CS-NB方法對軟件缺陷數據的預測性能嚴重依賴于誤分類代價的選擇。但在實際應用中，有標記數據只占數據集的一部分，傳統的代價敏感方法難以確定適合整個數據集的最優誤分代價。因此，本文提出的方法將傳統代價敏感方法所忽略的未標記數據充分利用起來，自適應地搜索適合整個數據集的最優誤分代價。用表5中的最優誤分代價構建CS-NB模型，λ的值取0.2，進行下一步的對比實驗。實驗結果如表6所示，每個數據集上的最好結果加粗標出。

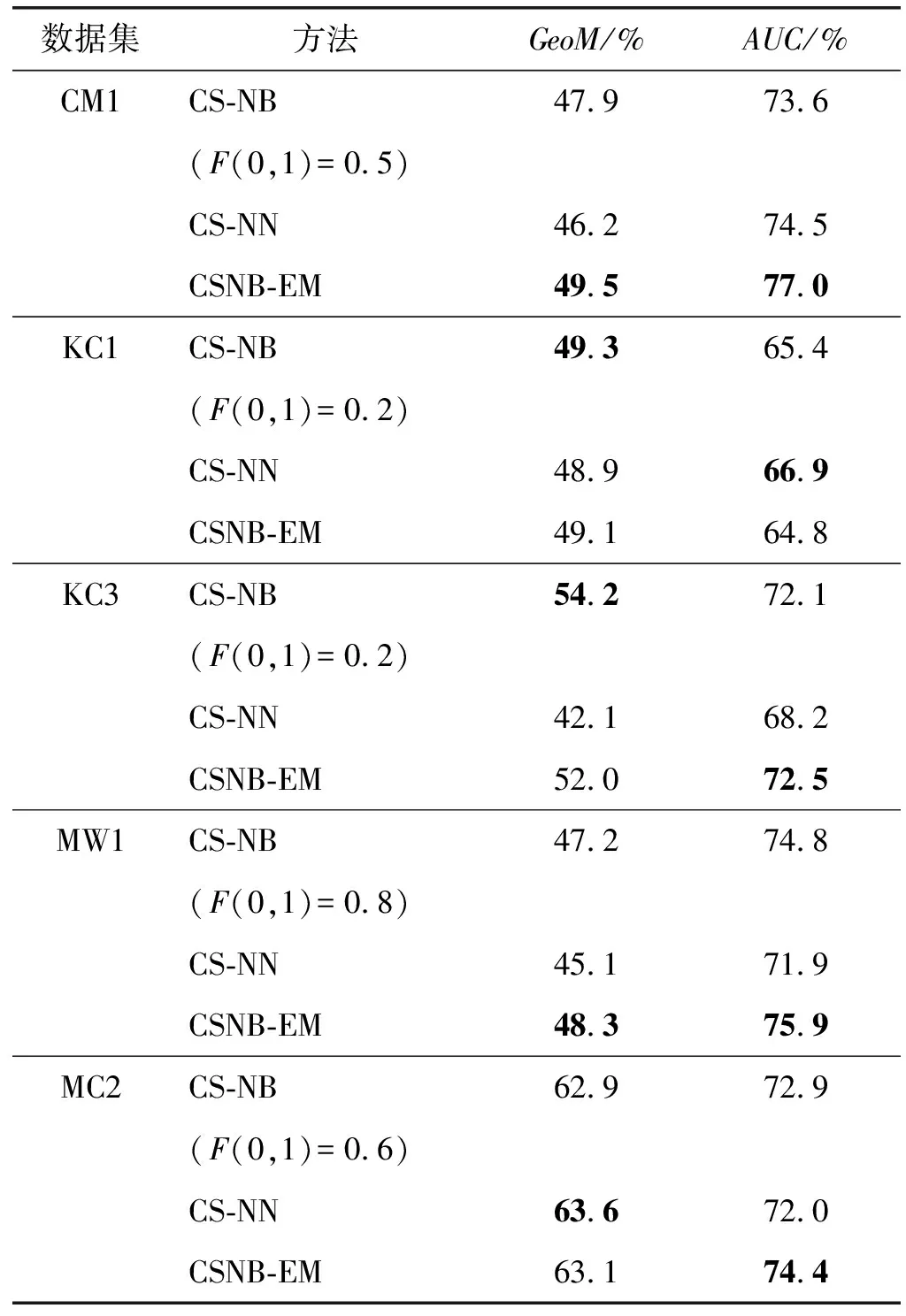
表6 模型性能

可以看出，在KC1與KC3數據集上，CSNB-EM模型的性能接近于用最優誤分類代價構建的CS-NB模型，而在CM1、MW1、MC2三個數據集上CSNB-EM模型達到了比CS-NB模型更高的GeoM與AUC指標。這充分說明了CSNB-EM方法自適應調整模型參數的良好效果。雖然未標記數據的實際標簽無法獲取，不能直接判斷最優誤分類代價，但CSNB-EM方法利用未標記數據迭代調整誤分類代價，同樣構建了性能良好的分類模型。在CM1、MW1、MC2三個數據集上，CSNB-EM方法有更好的性能是由于方法還利用未標記數據調整先驗概率P(c)與條件概率P(a|c)，構建的模型更能適應整個數據集。另外，CS-NN方法在MC2上的GeoM略高于CSNB-EM方法。在KC1數據集上，CS-NN的GeoM與CSNB-EM方法相當，而AUC指標超過CSNB-EM方法2.1百分點。KC1上CSNB-EM方法的性能低于CS-NN的原因是EM算法對初始值的敏感性，得到的模型參數會受到在訓練數據集上決定的初始模型參數的影響。在表6中還可以看出，所有方法在MC2上都取得了較好的GeoM性能，這與數據不平衡程度有關。在表3中MC2的不平衡度是1.841，是所有數據集里最小的，方法在相對平衡的數據集上更容易良好地折衷Recall與Precision的值，所以MC2上的GeoM明顯高于其他數據集。

3.3 λ對模型性能的影響

本實驗的目的是驗證訓練參數λ對CSNB-EM算法性能的影響。λ是本文在M-step修正模型參數時賦予未標記數據的權值，用來減弱未標記數據的影響。在實驗數據中取20%的樣本作為訓練數據，分別用不同的λ值訓練模型。實驗結果如圖2所示。可以看出，λ取得過高或過低都會對模型性能產生影響，在每一個數據級上，都是λ=0或λ=1的模型性能最低。當λ=0.2或λ=0.4時模型效果較好。當λ的值過低時，未標記數據對模型的修正作用有限。實際上，當λ=0時，CSNB-EM算法相當于用監督學習的方法構建模型。另外，由于未標記數據的數量明顯大于訓練數據的數量，λ取值過大會使得未標記數據對模型參數的影響過大，用未標記數據調整模型參數反而會降低模型性能。從圖2中還可以看出，由于MC2數據集的不平衡程度較小，模型在MC2上的GeoM性能十分突出。

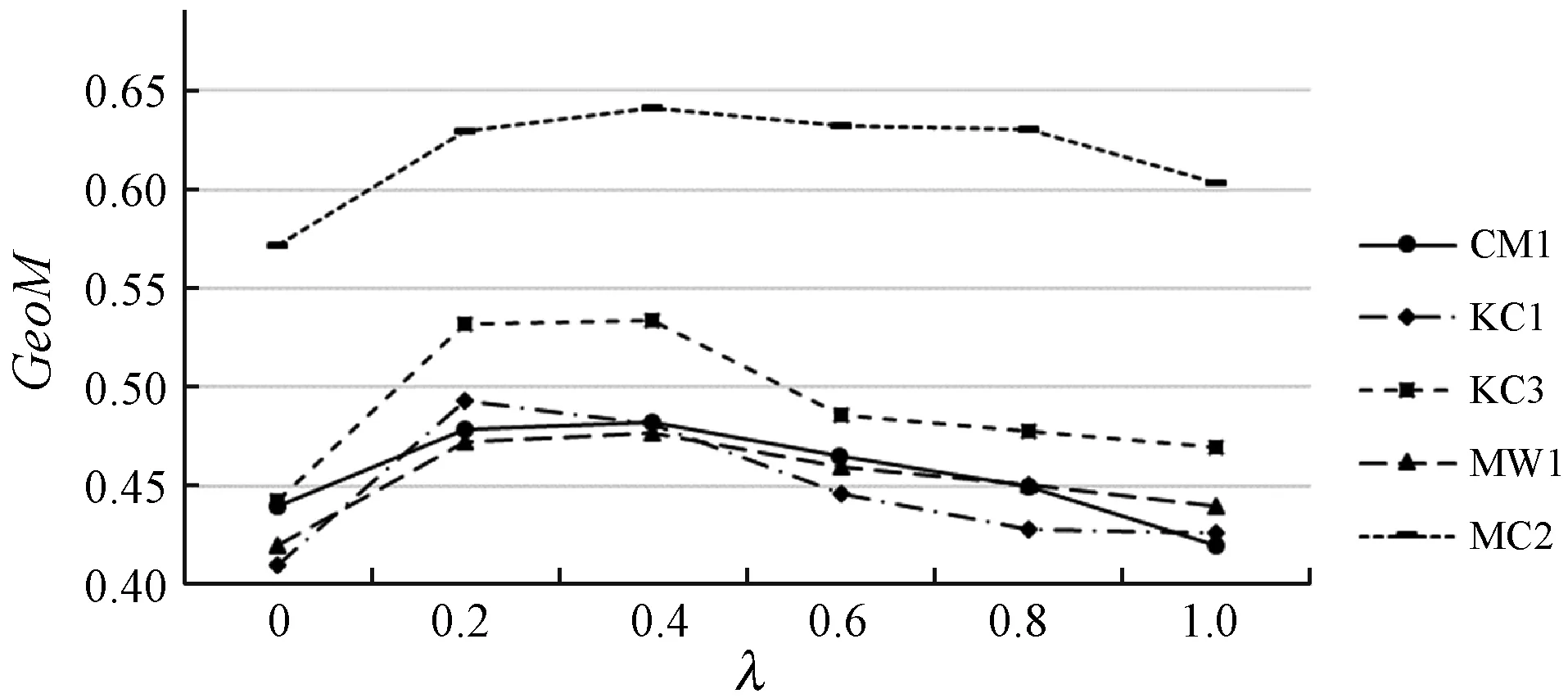
(a) GeoM

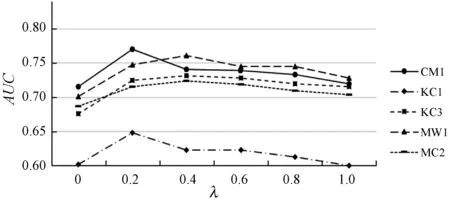
(b) AUC圖2 λ對模型性能的影響

3.4 CSNB-EM方法的收斂性

本節通過實驗驗證方法的收斂性。在每一輪訓練結束時都記錄下當前模型在數據集中的性能。如圖3所示，方法構建的模型總能同時在AUC與GeoM兩個指標收斂到一個最優性能，同時收斂速度非常快，在每一個數據集上都在10次迭代之內基本收斂。實驗結果表明，CSNB-EM方法具有良好的收斂性。

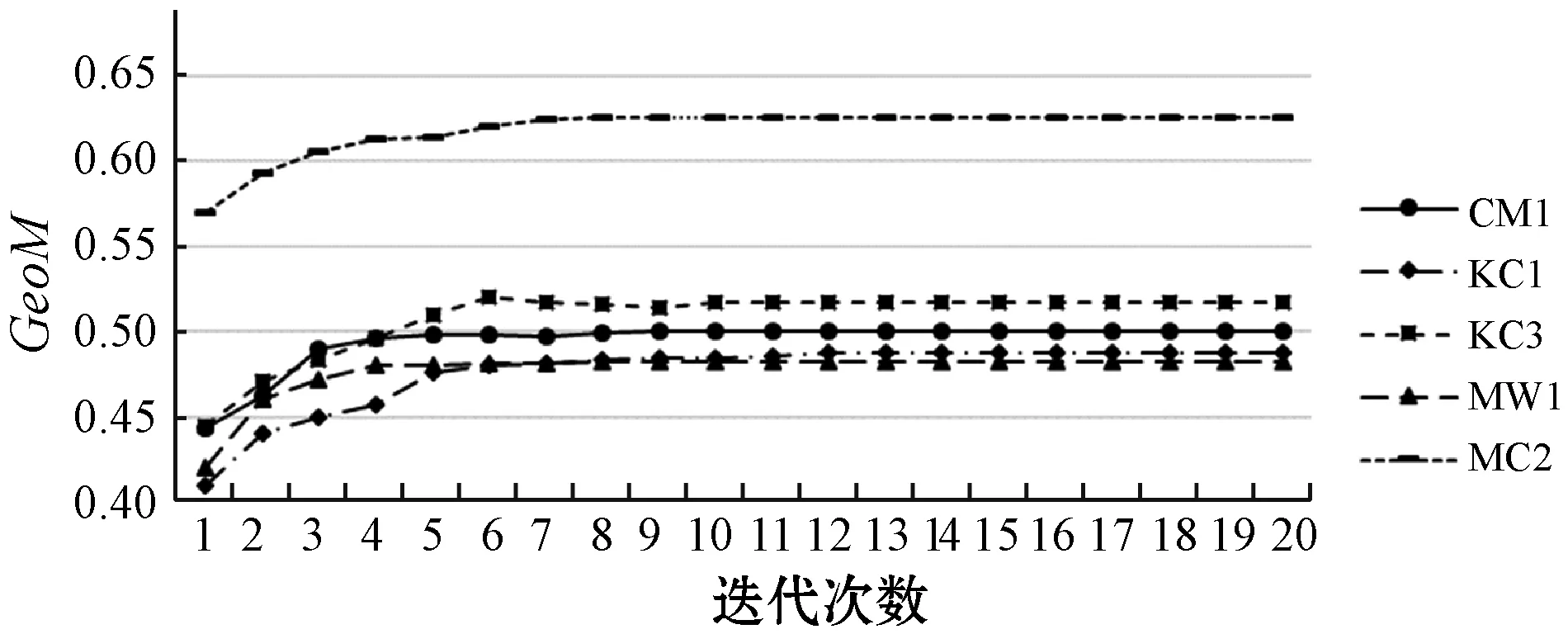
(a) GeoM

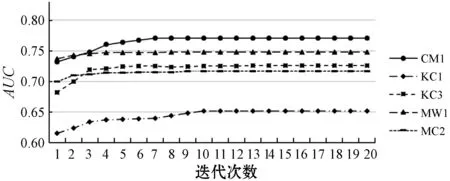
(b) AUC圖3 CSNB-EM方法的收斂性

4 結 語

本文針對目前軟件缺陷預測研究當中存在的誤分類代價難以確定的問題，提出一種動態調整誤分代價的半監督學習方法(CSNB-EM)。方法同時利用訓練數據與未標記數據迭代優化模型參數，并且自適應地確定誤分類代價的合理取值。在公開的MDP軟件缺陷數據集的5個項目上進行實驗，基于AUC與GeoM測評指標估計模型性能。實驗結果表明，CSNB-EM算法與CS-NB、CS-NN等現有的軟件缺陷預測算法相比，其構建的缺陷預測模型性能有明顯提高。