基于局部空間變換網絡的醫學圖像配準

張 糾 劉曉芳* 楊 兵

1(中國計量大學計算機應用與技術研究所 浙江 杭州 310018) 2(中國計量大學電子信息與通信研究所 浙江 杭州 310018) 3(浙江省電磁波信息技術與計量檢測重點實驗室 浙江 杭州 310018)

0 引 言

基于計算機輔助技術的醫學影像分析為病灶識別與定位[1]、疾病診斷[2-3]等提供了可靠的信息基礎。其中，醫學圖像配準是指對浮動圖像(Moving image)進行空間變換，確定浮動圖像與固定圖像(Fixed image)的空間對應關系[4]，尋求最佳空間映射。

醫學圖像配準問題的核心在于如何確定圖像間的相似性以及如何對圖像進行空間映射[4]，在臨床應用中，通常將同一個人在不同時間段所獲得的圖像進行配準或將多個人配準到標準圖譜上。傳統基于灰度值的配準方法[5]將配準問題抽象為最小化相似度測量以尋找最優參數的優化問題，然而，此種方法存在效果較差，無法取得最優解等局限性問題。近年來，由于神經網絡具有能夠從圖像特征中學習復雜映射、自動優化配準參數、建立優化模型等優點，提供了用于處理配準問題的新思路，已被廣泛用于醫學圖像配準中[6-8]。

基于編碼-解碼結構的卷積神經網絡如U-net[9]能夠自動對輸入圖像進行底層特征提取，其獨特的網絡結構在處理醫學圖像解剖結構相對固定、數據量較少的情況下具有較好的擬合性能。空間變換網絡(Spatial Transform Networks, STN)[10]是一種結合卷積運算、仿射變換、空間采樣的顯式特征空間變換網絡結構，其常用于特征提取網絡之后，對配準場(Registration Field)進行空間變換得到配準圖像(Registered Image)，以確定圖像間的空間映射關系。基于空間變換網絡的編碼-解碼結構是處理醫學圖像配準的常用網絡框架，然而，此類網絡具有沒有充分考慮到各通道特征重要性不同、基于單路的特征空間變換對局部圖像特征變換能力不足，以及特征與特征之間信息融合程度不高等問題，針對此問題，本文提出一種基于特征塊局部空間變換的雙路編碼-解碼網絡用于配準問題，本文方法在圖像特征塊的基礎上，進行了特征重要性加權和基于雙通道的局部特征空間變換。

1 相關工作

1.1 醫學圖像配準

醫學圖像配準是后續圖像融合，疾病診斷的基礎，其目標是根據浮動圖像與固定圖像之間的相似性關系，確定兩幅圖像間的最佳映射。根據空間變換的類型，醫學圖像配準方法可分為剛體配準與非剛體配準[11]。剛體配準方法具有變換參數較少、運算效率高等優點，然而，大多數醫學圖像如心臟CT(Computed Tomography, CT)圖像都存在非剛體變換，因此對于基于非剛體變換的配準方法研究較多。

傳統基于灰度值的配準方法采用互相關系數(Cross Correlation)[12]等相似性測量指標，通過優化參數模型確定最終映射關系，此外，互信息(Mutual Information)[13]及其改進的條件互信息(conditional Mutual Information)[14]、最大梯度距離(Maximum Distance-Gradient, MDG)[15]、熵圖像(Entropy Images)、流行學習(Manifold Learning)[16]等也常用于醫學圖像配準問題中。

神經網絡本質上也是一種參數優化模型，其優點是能夠通過最小化損失函數自動學習優化參數，建立圖像間的配準模型。近年來，神經網絡在處理配準問題上表現出較好的學習性能，如遞歸級聯網絡[17]通過網絡級聯的方式逐層對圖像特征進行空間變換，在肝臟配準問題上表現出較好的泛化性能，遞歸配準網絡[18]將遞歸神經網絡引入圖像配準問題中，將圖像看作一系列序列模型。

醫學圖像配準常用的網絡框架如圖1所示，采用基礎特征提取網絡得到配準場，通過最小化損失函數得到浮動圖像與固定圖像間的空間映射參數。

圖1 醫學圖像配準框架

1.2 基于空間變換網絡的編碼-解碼配準模型

基于編碼-解碼結構的網絡模型如U-net[9]、SegNet[19]等，利用跳躍連接(Skip Connection)結構融合同級之間不同分辨率的特征，利用高分辨率特征具有輪廓、梯度、顏色等信息，低分辨率特征具有抽象化特征信息，將兩者的語義信息融合，使融合后的特征同時具有高層與底層特征的語義信息，能夠對原始輸入圖像做出精細化特征表達。

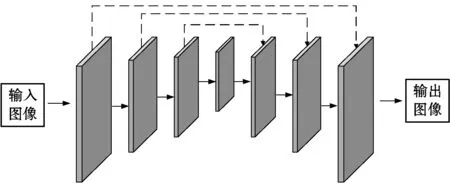
圖2 編碼-解碼網絡結構

圖2為編碼-解碼網絡基本結構，其整體可分為三個組成部分：特征編碼，特征解碼，特征融合。一般來說，輸入圖像與輸出圖像具有相同或相近大小分辨率，輸入圖像經過卷積、激活函數、下采樣等運算后得到編碼后的圖像特征，下采樣的次數一般為3到4次。過多的下采樣次數導致參數數量增加，計算速度減慢；過少的下采樣次數導致提取到的特征不足以表征圖像的深層細節。最大池化(max-pooling)是常見的下采樣運算，可看作正則化的一種方式。卷積運算是實現圖像特征提取的關鍵，其數學表達式如下：

(1)

式中:x為輸入圖像；k為卷積核；z為輸出圖像。基于編碼-解碼結構的卷積網絡通常采用跳躍連接的方式進行特征融合，其數學表達如下：

(2)

式中:X表示編碼層級的特征；Z表示解碼層級的特征；O表示通道拼接后的融合特征。

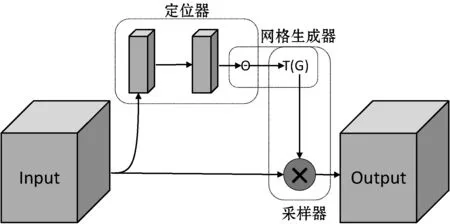
圖3 空間變換網絡基本結構

圖3為空間變換網絡結構，空間變換網絡是一種針對圖像特征變換的通用網絡模塊，能對輸入圖像進行仿射變換，由于其采用卷積、全連接等運算，使得空間變換網絡可以擬合復雜函數映射，輸出變換參數，得到空間變換后的圖像特征。空間變換網絡整體由定位器、網格生成器、采樣器三部分組成。

1) 定位器通過卷積等運算，輸出輸入特征與輸出特征之間的變換參數：

(3)

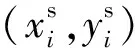
2) 網格生成器根據仿射變換矩陣以及輸出特征空間坐標，計算與之對應的輸入特征空間坐標。

3) 采樣器根據網格生成器得到的空間坐標點，利用雙線性插值對輸出特征進行填充：

(4)

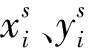
2 基于特征塊空間變換的配準模型

2.1 網絡結構

基于空間變換網絡的編碼-解碼網絡沒有考慮到不同通道的特征重要性不同，此外，空間變換網絡針對整個輸入特征，局部特征空間變換能力不足。針對此問題，本文提出了一種基于特征塊的雙通道空間變換網絡(Feature Patch Based Dual-channel Spatial Transform Network, FPDC-STN)。結合編碼-解碼網絡，本文的配準模型結構如圖4所示。

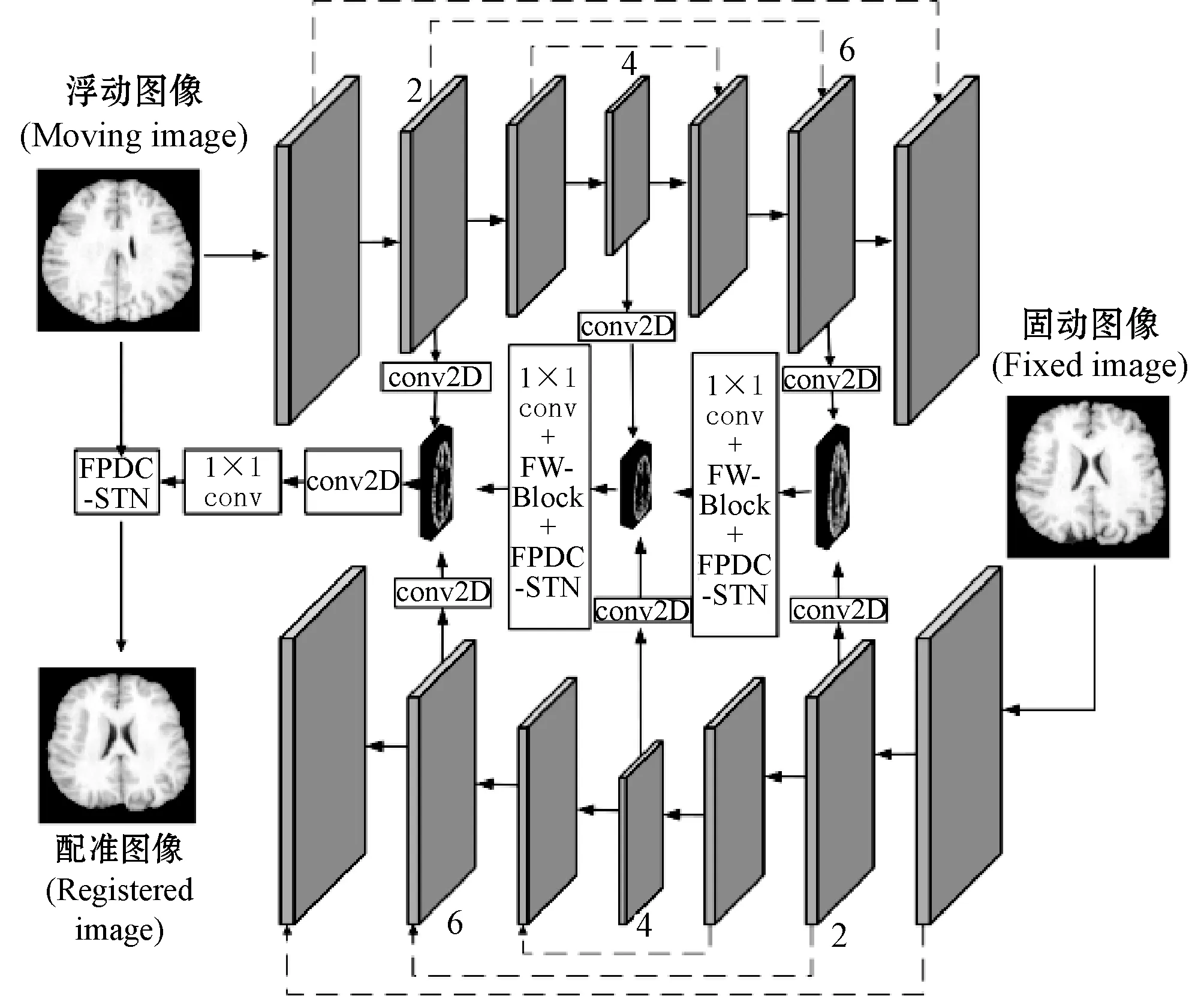
圖4 基于特征塊的雙通道空間變換網絡配準模型

本文模型采用兩個編碼-解碼結構的卷積神經網絡分別對浮動圖像和固定圖像進行特征提取，同時將固定圖像的特征編碼部分與浮動圖像的特征解碼部分對齊，組成對稱網絡。為提高特征利用率，借鑒特征金字塔網絡[20]思想，從固定圖像和浮動圖像的編碼-解碼網絡中分別抽取了第2、第4、第6層特征，兩者特征融合之前用二維卷積進行了特征空間轉換。圖4中，FW-Block為特征加權(Feature Weighting)模塊，FPDC-STN為本文提出的特征塊雙通道變換模塊，兩者的網絡結構如圖5、圖6所示。

特征加權模塊對原始輸入特征的通道加權可以分為4步：1) 對于輸入特征，采用兩個不同尺寸的分組卷積核得到兩組不同的輸出特征，并設置分組數K對兩組輸出特征進行分組，分別得到K個特征塊；2) 利用式(5)對特征塊進行全局平均池化(Global Average Pooling, GAP)，得到特征加權參數；3) 使用全連接和激活函數等對特征塊進行通道加權，如式(6)所示；4) 分別對K個特征塊進行合并，采用通道拼接的方式得到原始輸入特征通道加權后的輸出特征。

(5)

式中：H表示輸入特征塊的高；W表示輸入特征塊的寬；UC表示某個通道的特征塊；ZC表示某個通道的輸出特征塊。

O=σ(g(Z,w))=σ(w2δ(w1Z))

(6)

式中：Z表示輸出特征塊；w1、w2表示全連接參數；δ表示非線性激活函數如ReLU等；σ表示Sigmoid函數。

借鑒空間變換網絡結構的思想，本文采用了基于特征塊空間變換的方式對原始輸入特征進行空間變換。此外，針對原始空間變換網絡感受野大小固定的局限性問題，本文還提出了一種基于雙通道的空間變換網絡，基于權值共享方式將特征塊空間變換與雙通道策略結合形成最終的基于特征塊的雙通道空間變換網絡(FPDC-STN)。FPDC-STN對輸入特征的空間變換可分為以下3步：1) 采用兩個不同尺寸大小的卷積核(3×3，5×5)對原始輸入特征進行分組卷積，然后對特征進行分塊；2) 對每個特征塊，分別進行空間定位-網格生成-采樣操作，得到空間變換后的輸出特征塊；3) 對輸出特征塊進行合并，基于通道拼接的方式得到最終空間變換后的輸出特征。

2.2 損失函數

本文所用的損失函數包括兩部分，分別為衡量浮動圖像與固定圖像之間的相似性指標Lsin(φ)，配準場的正則化項Lsmooth(φ)。兩者分別定義如下:

Lsim(F,R,φ)=-CC(F,R(φ))=

(7)

(8)

式中:CC(F,M(φ))表示局部相關系數(Correlation Coefficient)，衡量配準圖像R(φ)與固定圖像F之間的局部相關性；φ表示配準場(Registration Field);pi表示索引為i的像素。總損失函數定義為相似性指標Lsim(φ)與正則化項Lsmooth(φ)之和，如式(9)所示，λ為正則化參數。

L(F,M,φ)=Lsin(F,M,φ)+λLsmooth(φ)

(9)

2.3 整體算法流程

本文提出的基于局部空間變換網絡的醫學圖像配準算法整體流程如圖7所示。

圖7 本文整體算法流程

Step1輸入數據集劃分參數train_rate、validate_rate、test_rate，將數據集劃分為訓練集、驗證集、測試集。

Step2對訓練數據進行數據增強，包括圖像旋轉、圖像扭曲等。

Step3對待配準圖像進行預配準、去噪等預處理操作。

Step4初始化網絡參數、迭代次數Itr、正則化系數lamda等。

Step5更新網絡參數，以及分別建立特征塊雙通道變換模塊、特征加權模塊、特征編碼-解碼網絡。特征塊雙通道變換模塊(其中split_num表示劃分的特征塊數量)主要偽代碼表示如下(使用Pytorch框架編程)：

Apply 3×3 convolution and 5×5 convolution to input features;

Split input features into split_num;

# 空間定位

Location_module=nn.Squential(nn.Conv2d(1,8,3),

nn.MaxPool2d(2,2),

nn.Relu(True),

nn.Conv2d(8,10,5),

nn.MaxPool2d(2,2),

nn.ReLU(True))

#3*2 仿射變換回歸器

fc_loc=nn.Sequential(

nn.Linear(10 * 3 * 3, 32),

nn.ReLU(True),

nn.Linear(32, 3 * 2)

)

# 組合特征塊

Combine input features

特征加權模塊表示如下；

# 劃分特征塊

Split input features into split_num;

# 平均池化

avg_pool = nn.AdaptiveAvgPool2d(1)

# 特征加權以及特征賦值

fc=nn.Sequential(

nn.Linear(channel, channel // reduc tion, bias=False),

nn.ReLU(inplace=True),

nn.Linear(channel // reduction, channel, bias=False),

nn.Sigmoid()

)

# 組合特征塊

Combine input features

Step6網絡前向傳播獲得預測值。

Step7用式(9)計算損失函數，并計算配準評價指標。

Step8使用梯度下降算法，如式(10)所示，網絡反向傳播。

(10)

Step9迭代次數或損失函數是否滿足要求，若滿足要求，則執行Step 10，若不滿足要求，則執行Step 5。

Step10配準算法結束。

3 實 驗

實驗采用的硬件設備是顯存大小為12 GB的Nvidia GeForce GT1080ti GPU以及Intel i7 8700 CPU，軟件環境采用Python 3.6，機器學習處理包sklearn以及醫學圖像處理工具SimpleITK，配準實驗基于深度學習框架Pytorch[27]實現。初始學習率設置為0.000 01，并使用初始動量為0.9的Adam優化器。迭代次數設置為2萬次，并采用隨機梯度下降(Stochastic Gradient Descent，SGD)更新網絡參數，正則化系數λ設置為1.0。

3.1 數據集與實驗參數

本文分別在腦部數據以及肝臟數據上進行了配準實驗。肝臟數據集來自MSD[21]以及SLIVER[22]，腦部數據集來自ADNI[23]、ABIDE[24]、LBPA[25]。所有的數據重采樣為132×132×132分辨率大小，并用醫學圖像處理工具FreeSurfer[26]進行了包括初步配準、腦部區域提取等標準預處理步驟。提取肝臟掃描數據、腦部掃描數據總計1 000個，其中800個用于訓練配準模型，100個用于驗證模型，100個用于測試模型。此外，為了增加實驗數據，所有數據都進行一系列數據增強操作，如二維旋轉、中心裁剪、數據扭曲等。實驗樣例圖像如圖8所示。

圖8 實驗樣例圖像

3.2 評價指標

本文采用Dice系數評價配準與固定圖像之間的重合程度：

(11)

式中:Dice系數范圍為[0,1]。當Dice系數為1時表示配準圖像與固定圖像完全匹配，當Dice系數為0時表示配準圖像與固定圖像完全不匹配。

3.3 腦圖像配準實驗

本文評估了不同實驗參數對配準效果的影響，評價標準為驗證集Dice系數、一段時間后評價指標是否變化、網絡收斂時間。評估參數包括正則化系數λ、迭代次數、Adam優化器初始動量、學習率。結果如表1-表4所示。

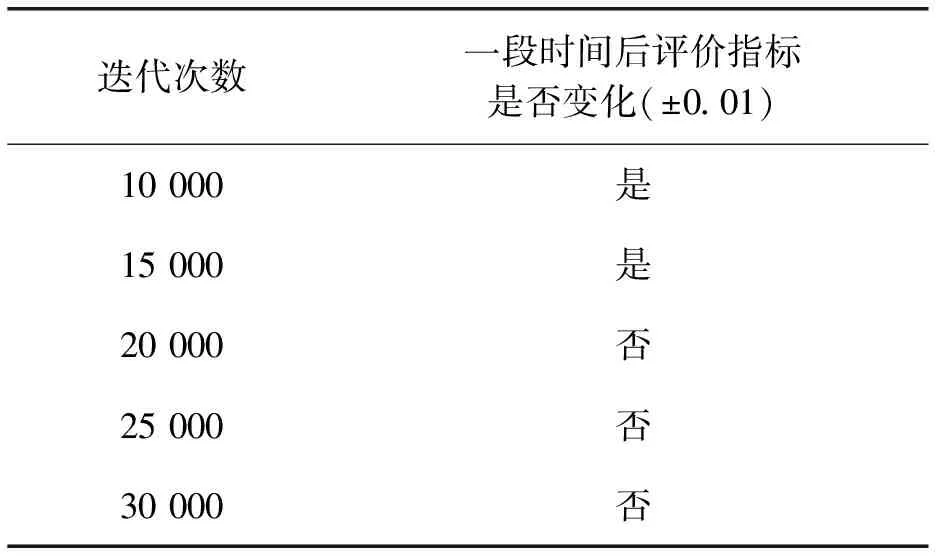
表1 迭代次數對配準精度的影響

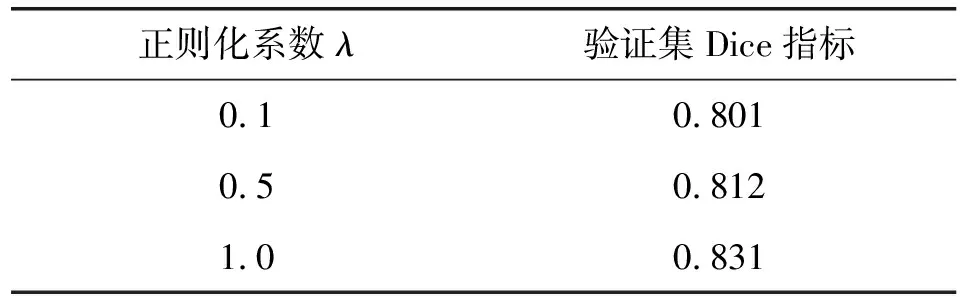
表2 正則化系數對配準精度的影響

表3 Adam初始動量對配準精度的影響

表4 學習率對配準精度的影響

根據表1可知，迭代次數為20 000次時，一段時間后驗證集評價不再變化，故本文設置的迭代次數為20 000次。根據表2可知，正則化系數λ=1時，驗證指標Dice系數最高，故本文設置的正則化系數為1。根據表3可知，Adam初始動量為0.90時，驗證集Dice系數指標最高，故本文設置的Adam初始動量為0.90。根據表4可知，學習率為0.000 01時，配準網絡已經收斂，并且驗證集Dice系數指標最高，當學習率為0.000 1時，雖然配準網絡已經收斂，但是其驗證集Dice系數低于學習率為0.000 01時Dice系數，故本文設置的學習率為0.000 01。

圖9為本文配準方法對于腦部圖像的配準結果，此外，為了說明本文配準模型的有效性與準確性，與UtilzReg方法[28]以及FAIM方法[29]進行了對比。

圖9 腦部圖像配準結果

本文選取了兩個切片的配準結果如圖9第一行以及第二行所示，圖9中第三行是第二行配準結果的局部放大圖。從固定圖像與浮動圖像中可以看出，固定圖像的外形輪廓與浮動圖像有較大差別，兩者內部組織結構也不相同，固定圖像內部組織如腦白質、腦灰質等紋理較為簡單，而浮動圖像內部組織的紋理比較復雜，這對配準算法的空間變換性能提出了較高要求。

圖9(c)為本文提出的配準方法的配準結果，本文方法可以針對浮動圖像與固定圖像之間的差異，對浮動圖像的外部輪廓以及內部組織紋理進行準確的空間變換，這表明本文提出的基于特征塊的雙通道空間變換網絡FPDC-STN以及特征通道加權能夠捕捉圖像細節特征，對圖像局部做出準確配準。圖9(d)為FAIM配準方法的配準結果，可以看出，FAIM方法能夠根據固定圖像與浮動圖像之間的整體輪廓差異對浮動圖像做出較為準確的空間變換。然而，相比本文配準方法，FAIM方法針對圖像局部細節處理仍顯不足，配準結果中局部細節與浮動圖像差異不大，這說明FAIM方法不能準確地根據局部圖像細節對浮動圖像進行空間形變。圖9(e)為UtilzReg方法的配準結果，整體來說，此方法與FAIM方法差距不大，在處理圖像配準細節上較差。

表5為本文方法與FAIM方法以及UtilzReg方法的評價結果，本文進行了10次重復實驗，對配準結果計算Dice指標的平均值以及標準差。可以看出，本文方法所取得的平均Dice指標相比FAIM方法提高2.7%，相比UtilzReg方法提高1.4%，在幾種方法中取得最高的Dice系數。從配準穩定程度上看，本文的Dice指標的標準差最小，也是三種配準方法中最穩定的算法。

表5 各方法腦部配準評價

3.4 肝臟圖像配準實驗

圖10為本文在肝臟圖像上的配準結果，同時也與FAIM算法以及UtilzReg算法比較了肝臟圖像配準的有效性與準確性，結果如表6所示。

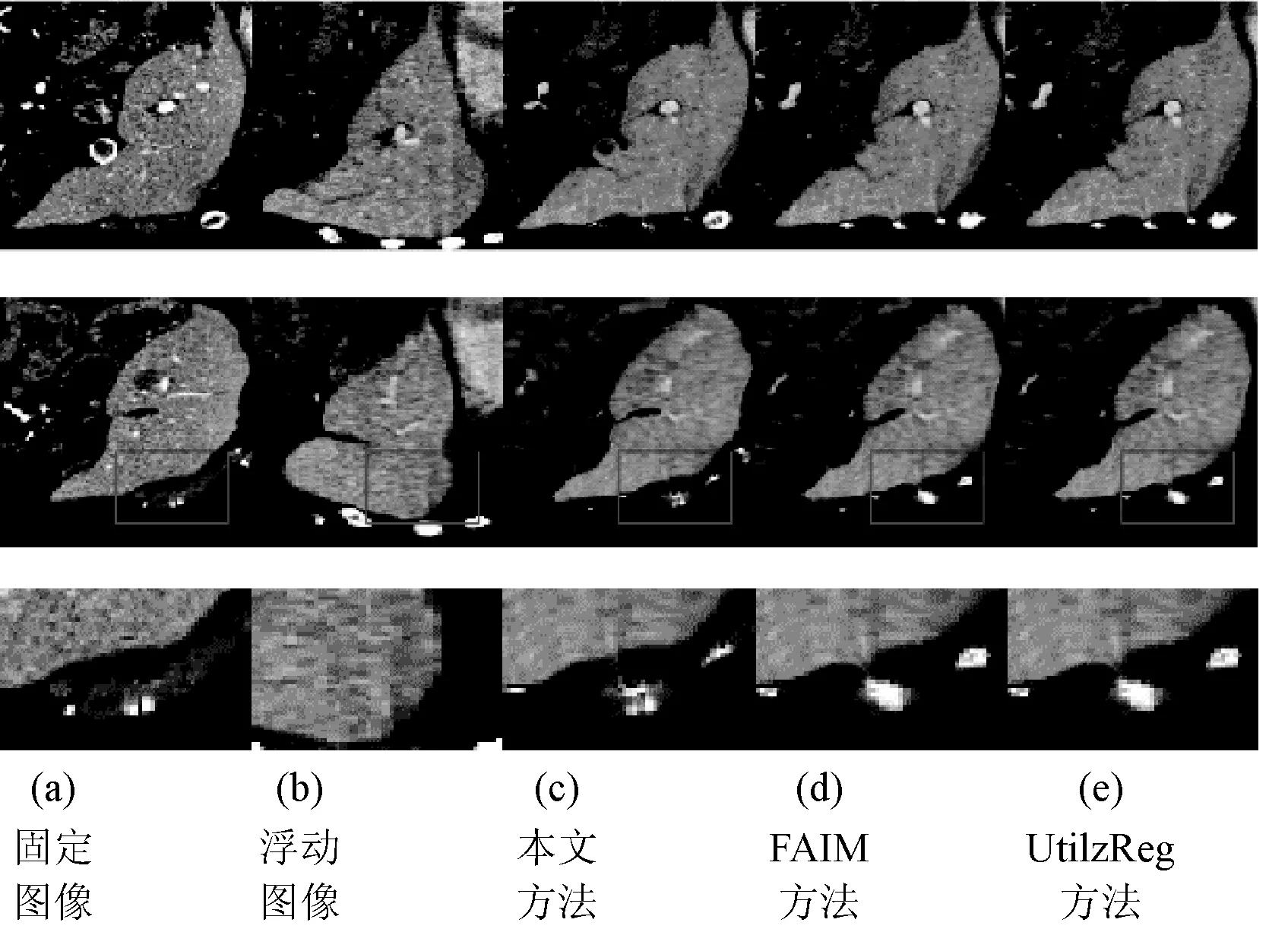
圖10 肝臟圖像配準結果

表6 各方法肝臟配準評價

圖10第一行與第二行為選取的部分切片圖像配準結果，第三行為第二行配準結果的局部放大圖。可以看出，本文配準方法能夠較準確地處理圖像細節，如圖10(c)所示，針對固定圖像中的局部亮點，本文配準方法能夠對浮動圖像進行局部空間變換，配準結果與固定圖像差異不大。對于FAIM以及UtilzReg方法，兩者能較好地對肝臟整體輪廓作出形變，但是在處理局部細節時仍然存在較多孤立像素點以及局部空間變換不足等問題。表6表明，與FAIM配準方法相比，本文方法平均Dice系數提高了8.5%，與UtilzReg方法相比，本文方法提高了3.6%。本文方法在保持最高平均Dice評教指標的同時，具有較好的穩定性。

4 結 語

本文在現有基于空間變換網絡的編碼-解碼配準模型基礎上，提出了針對特征融合的特征加權模塊以及基于特征塊的雙通道空間變換網絡FPDC-STN；針對空間變換網絡無法有效解決圖像局部空間變換、感受野有限，以及空間變換參數無法共享等問題，本文提出的基于特征塊的雙通道空間變換網絡能夠針對拆分的特征塊進行準確局部變換；同時，利用雙通道策略以及兩種尺寸大小不同的分組卷積策略，共享空間變換網絡，有利于減少網絡參數量和提高網絡的空間變換能力。此外，本文提出的特征加權模塊以及特征塊變換模塊通過兩個大小不同的卷積核，獲取不同大小的感受野，本文提出的配準算法可以對自然圖像和醫學圖像進行特征變換和特征加權，作為具體應用實例，本文在醫學圖像上驗證了其配準有效性和準確性，進一步提升了圖像的空間變換性能，提高了圖像的配準精度。