基于動態注意力網絡非負矩陣分解的抑郁癥篩選

王鳳琴 柯亨進

1(湖北師范大學物理與電子科學學院 湖北 黃石 435106) 2(武漢大學計算機學院 湖北 武漢 435001)

0 引 言

諸如癲癇[1]和嚴重抑郁癥[2]等腦健康問題持續受到科研工作者和醫療界的關注，其早診斷進而早治療在改善健康方面起著舉足輕重的作用。特別地，對于嚴重抑郁癥來說，準確預知大腦狀態可以大大降低患者自殺的風險，致使其成為神經科學研究和臨床實踐所追求的目標。

同步現象廣泛存在于大腦各區域及其相互作用過程當中。研究表明，對于認知功能受損的各種腦疾病而言，其往往呈現出與正常人不同的腦電同步模式[3-4]。在度量二元變量關系上，最大信息系數(Maximal Information Coefficient)被證明是最有效的關聯強度度量[5],尤其是對非線性關系和受高噪聲污染數據的相關性度量上。近幾年，多變量同步分析方法有了長足發展，如相同步聚類分析(PSCA)、S估計子[6]和相關矩陣分析(CMA)[7]。其中，S估計子能有效度量全局同步，但缺乏對變量間同步細節的度量；PSCA可以獲取不同變量的拓撲細節，但在全局同步信息度量方面存在明顯不足；而CMA兼顧以上優點。

矩陣分解將高維空間的特征映射到低維子空間中，常用的矩陣分解方法有主成分分析、線性判別分析、非負矩陣分解[8]和奇異值分解等。其中，由于非負矩陣分解首次添加非負限制且具有良好的解釋性而受到廣泛關注。在此基礎上，很多學者對其進行了算法改進。其主要的改進方向是增加正則條件，如稀疏性、圖正則[9]、正交性等，已成功運用在圖像處理和神經信息處理中。然而，這些方法假設數據服從均勻分布，只關注如何提高分解后數據的稀疏度，缺乏對感興趣特征的著重刻畫。

注意力機制是當前深度學習領域的最新成果，它可以幫助模型更好地捕捉和增強感興趣特征，從而優化模型結構。其主要機制是對輸入進行加權。注意力機制早在2014年成功應用于機器翻譯任務中，之后受到廣大學者的關注，產生了很多形式的變體和改進算法[10-11]。為了快速地對圖像的關鍵區域進行超分辨率分析，一種基于自適應注意力機制的循環神經網絡被提出[12]，該模型通過自我強化的注意力機制自適應選擇并提取圖像中的重點區域或位置點的相關特征，提升對圖像的識別率。

在進行矩陣分解時獲取全局特征的同時引入自注意力機制充分了解細節信息提供了新思路。為此，本文首先利用最大信息系數計算腦電所有通道之間的同步值，以此構造相關同步矩陣，利用自編碼器提取相關同步矩陣的注意力，最后利用哈德曼積應用于非負矩陣分解算法中實現基于注意力網絡的非負矩陣分解(ANMF)。本文所給出的實驗結果是在抑郁癥公共數據集MPHC上進行驗證評估的，本文所提出的方法獲得94.45%精確度、96.47%敏感度和92.31%特異度，超過了現有方法的分類性能(基于相同數據集)。其主要貢獻如下：

(1) 提出一種可以刻畫矩陣非線性動態注意力方法，該方法能夠強化感興趣區域特征，而抑制對問題求解無關的信息；

(2) 設計一種基于注意力機制的矩陣分解方法，自適應地將注意力集中于當前相關中對抑郁癥分類更具價值的區域，從而快速做出正確的決策；

(3) 為了充分利用非負矩陣分解提取出的相關矩陣的低秩表達，設計多分支神經網絡，并成功應用于抑郁癥篩選，其分類性能超過現有方法。

1 方 法

本文方法的技術細節主要包括：(1) 度量兩兩通道間的同步關系(最大信息系數)，并構造全腦相關矩陣；(2) 構建基于自編碼器的非線性注意力；(3) 實現基于動態注意力的非負矩陣分解算法；(4) 設計層次卷積神經網絡對抑郁癥分類。

1.1 總體設計

為有效地進行EEG分析，本文試圖：(1) 最小化傳統EEG預處理過程(去掉了傳統EEG預處理中必須包含依賴足夠的先驗知識而進行的去噪、去干擾和去偽跡過程)；(2) 最小化超參數的設置以方便臨床應用。圖1顯示了所提方法的整體設計，其主要包括如下三個階段：① 同步特征的特征提取；② 基于自編碼器的注意力發現；③ 對結果進行評估。具體過程如下，原始EEG數據被劃分為同等時間窗口大小的片段，對片段內所有的通道計算相互之間的最大信息系數(同步值)，根據通道位置將所有同步值組織成相關矩陣，構成系統的特征矩陣。利用神經網絡的非線性擬合能力構建基于自編碼器的注意力發現機制，應用此注意力機制實現基于注意力機制的非負矩陣算法，該算法提取了相關矩陣的最重要的感興趣特征，最后設計分層卷積神經網絡分類器實現不同模態特征的處理，并實現抑郁癥的早期發現。

圖1 系統流程

1.2 最大信息系數

最大信息系數是基于最優劃分的互信息[5]，它能夠快速檢測數據間的關聯關系，具有抗噪性、非線性以及有效性[5,13]。本文首先計算兩兩通道之間的MIC，以度量通道間的同步值。

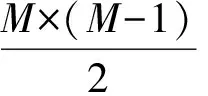
(1)

式中：MICij(i,j=1,2，…,n)表示兩通道i、j之間的同步關系。依據MIC的性質，CMMIC是一個正定對稱矩陣：MICij≥0&&MICij=MICji&&MICii=1。存在一個極其特殊和稀少的情形：當所有通道之間滿足線性無關時，CMMIC退化為單位陣。CMMIC滿足如下性質：

非負性：所有的特征值都非負，即λ≥0;

1.3 基于自編碼器的非線性注意力

刻畫同步矩陣中感興趣重要特征是提高分類性能至關重要的先決條件。為此，需要設計方法，使其將廣泛的上下文相關信息編碼為局部特征，從而增強特征的表達能力。

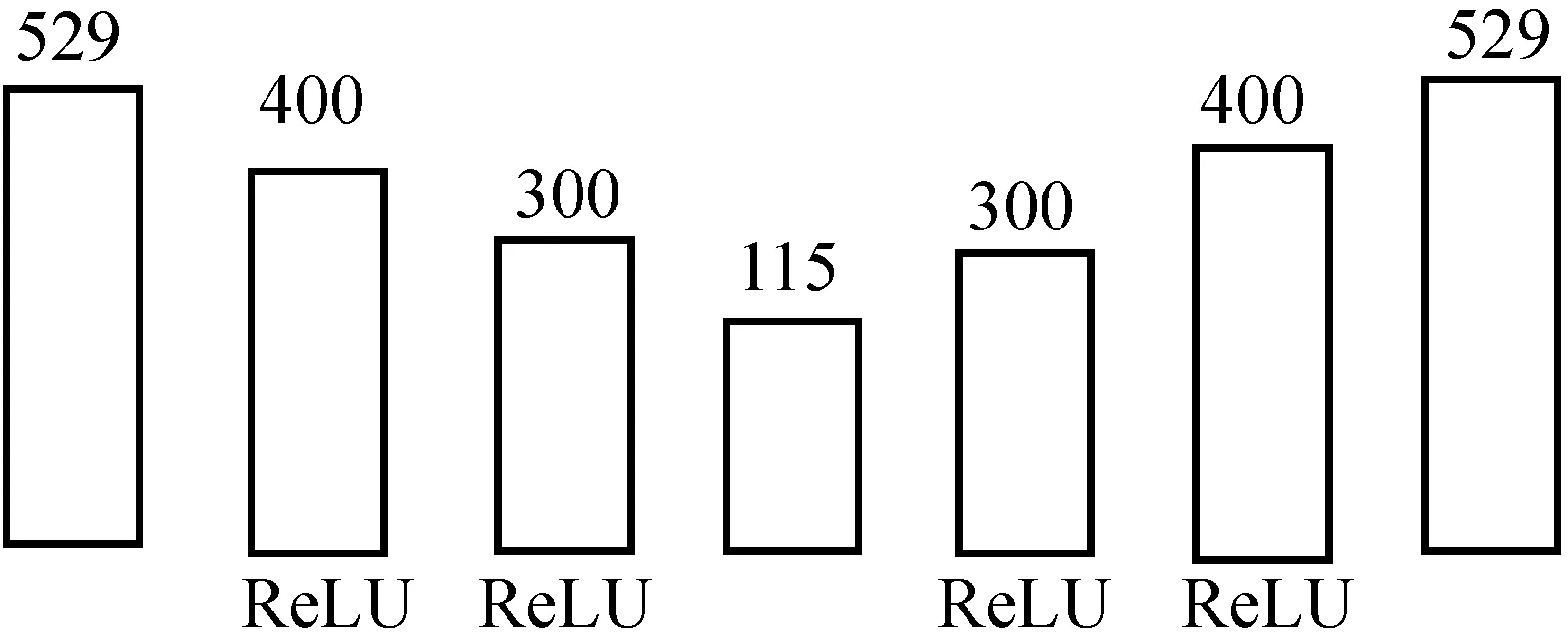
圖2 基于自編碼器的非線性注意力機制

本文的非線性注意力模型的結構如圖2所示，圖中的數字表示當前層中包含的隱含神經元的個數，下方文字表示激活函數ReLU，當前層下方空白表示當前層沒有設置激活函數，其本質上是一個自編碼器。自編碼器是一種無監督的學習算法，由編碼器和解碼器構成，編碼器旨在把一個不定長的輸入序列X轉化成一個定長的向量C，解碼器旨在利用編碼器的輸出復原成一個與輸入序列相同的向量R。

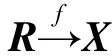
(2)

式中：f(·)表示神經網絡的非線性擬合函數。

f(·)的求解依靠神經網絡模型參數的更新來完成，在自編碼器中，其利用復原向量R與輸入向量X之差，基于反向傳播算法驅動神經網絡模型參數的更新:

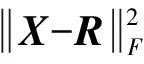
(3)

當達到穩定時，編碼器的輸出構成了輸入向量的低維表達。換句話說，其代表了原始輸入的最重要的特征。從另外一個角度看，它也能看作為輸入向量的注意力。

1.4 基于動態注意力的非負矩陣分解算法

非負矩陣分解(NMF)最早由Lee和Seung于1999年在自然雜志上提出的一種矩陣分解方法[8]，它分解矩陣所得的所有特征均為非負值，增加問題的物理解釋性。它已成為神經信息學、計算機圖像處理和信號處理等研究領域中最受歡迎的特征降維工具之一。

傳統NMF在分解過程中，并未考慮注意力機制，也即假設要分解的數據滿足均勻分布。然而，現實世界的數據往往呈現出多變量分布模式，致使傳統NMF無法增強對感興趣特征的提取。因此，本文在基于注意力的非負矩陣分解算法(ANMF)中引入注意力機制，試圖減弱矩陣中的某些元素，而變相地增加其他元素的值。其目的是矩陣的特征增強提取，首先利用原始信號V與基于注意力D的復原矩陣之間的相對殘差：

E=V-(D°W)(DT°H)wij≥0,hij≥0

(4)

式中：D和DT分別表示作用于矩陣W和H的注意力矩陣，也是1.3節中自編碼器中編碼器的輸出向量重塑而出的矩陣；° 表示哈德曼積，其表達了注意力機制直接作用于分解矩陣。由于全腦同步相關矩陣CMMIC是對稱方陣，因此，D與W的維數相同，DT與H的維數相同。假設噪聲服從高斯分布,最大似然函數為：

(5)

取對數后：

((D°W)(DT°H))ij]2

(6)

假設各數據點噪聲的方差一樣，那么接下來要使得對數似然函數取值最大，只需要下面目標函數值最小。

(7)

為求解式(7)的梯度方向，需要先計算：

[ATAX+ATAX]ij=[2ATAX]

(8)

進而對W進行求偏導數：

(9)

同理可以得到：

(10)

根據牛頓法，其迭代的梯度下降公式如下：

Wik=Wik-α1[(DT°H)(DT°H)T(D°W)T-

D(DT°H)VT]ik

Hik=Hik-[(D°W)T(D°W)(DT°H)-

VT(D°W)DT]ikα2

(11)

當:

(12)

可以得到最終的分解矩陣更新公式：

(13)

而當D或者DT對應的位置為0時，Wik=0,Hik=0。

1.5 多分支卷積神經網絡

本文將腦電數據分類(抑郁癥和健康組)看作是二元分類問題。給定一個腦電時間片，本文的任務是決定其是否屬于抑郁癥還是健康組。類標簽1賦予抑郁癥組；而類標簽0則賦予健康組。腦電時間片首先計算兩兩通道之間的同步MIC值，進而構造全腦同步相關矩陣。對每個同步矩陣利用自編碼器提取其注意力，該注意力可以用來增強非負矩陣分解提取感興趣特征，而降低注意力以外的特征。

分類器旨在獲取高分類性能，且能夠同時處理多個因子矩陣。圖3顯示了多分支神經網絡的體系結構。它始于多分支子網，對于每一個由基于注意力網絡的非負矩陣分解所得的因子矩陣(矩陣大小分別為23×5和5×23)，都由每個子網進行處理，子網的最后一個卷積層輸出的矩陣被展平成一個長度為95的向量，兩路的向量拼接(融合)成一個長度為190的向量，構成一個全連接層，接著是兩層全連接層，最后，sigmoid激活函數輸出抑郁狀態。其主要設計規則如下：1) “多分支網絡”接受不同的因子矩陣，旨在抗噪聲和處理非平穩的多模式特征數據。2) “沙漏式”全連接層旨在快速縮減神經元的數目，以減少模型參數數目。越接近輸出層，神經元數據越少。本文中的“沙漏式”全連接層塊是分類器模型的最后幾層。

圖3 分類器體系結構

1.6 參數設置

關于注意力網絡和分類器的超參數設置問題，利用貝葉斯超參數優化[14]所得，其相關超參數大部分都顯示在相應的圖中(圖3和圖2)。分類器的訓練由基于動量(0.9)反向傳播的SGD優化器進行處理[15]。訓練過程通過權重衰減(1e-6)進行調整，相應的學習率為0.01。

非負矩陣分解是一個無監督分解算法，只需設置算法的停止條件。本文設置的停止條件為迭代次數為100或者分解誤差小于0.01。

2 實 驗

2.1 數據描述

公共數據集包含了嚴重抑郁癥患者和健康對照組的腦電數據(MPHC[16])，所有樣本都采集自馬來西亞塞因斯大學醫院的34個抑郁癥患者(17名男性，平均年齡為40.3±12.9)和30名健康受試者(對照組，21名男性，平均年齡為38.227±15.64)。該樣本集已經排除了那些有精神病癥狀、孕婦、酗酒者、吸煙者和癲癇患者的MDD參與者。健康對照組也篩選出了可能的精神疾病或身體疾病。腦電圖傳感器按照國際系統10-20在256赫茲的頻率下進行采集，該數據集中可能包含23個通道數據，本文采用了前面的20個電極(Fp1、Fp2、F3、F4、F7、T3、T5、C3、C4、Fz、Cz、Pz、F8、T4、T6、P3、P4、O1、O2、A2)。時間窗口設置為1 024(4秒)；因此，整個樣本空間被劃分成18 442個片段(其中抑郁癥的時間片:9 789，健康的時間片:8 653)。

2.2 計算復雜度

實驗所用的測試環境為英特爾i7CPU(3.33 GHz)、24 GB運行內存和64 bit Win7個人電腦。計算的主要過程包括注意力網絡的訓練、基于動態注意力的非負矩陣分解以及分類器的訓練三個部分。

注意力網絡和分類器都為神經網絡,它們的時間復雜度都基于子卷積神經網絡和子全連接神經網絡。因此，首先有必要討論子卷積神經網絡的時間復雜度。而其時間復雜度正比于網絡層數(L)及其相應的隱藏神經元個數(N)。整個子卷積神經網絡的時間復雜度計算如下[18]：

(14)

式中：l是卷積層的索引；d是深度;nl為第l層的過濾器的個數(也叫寬度);nl-1表示第l層的輸入通道的個數;sl和ml分別表示過濾器的空間大小以及輸出特征映射的大小(feature map)。

對于子全連接神經網絡，假設網絡的層數為L，每一層的神經元數為U，分類器的時間復雜度為O(UL)。

對于注意力網絡來說，其是一個全連接神經網絡，時間復雜度為O(UL)。關于層次分類器模型來說，其包括c子卷積神經網絡和一個子全連接網絡，所以其時間復雜度為：O(cS(N,L))+O(UL)，也即O(S(N,L))+O(UL)。

2.3 實驗結果

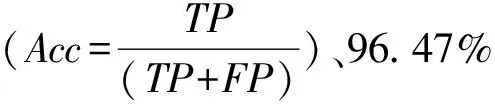
圖4顯示了分類器在嚴重抑郁癥數據集上的學習曲線。在這種情況下，分類器具有很好的泛化能力，并沒有產生過擬合或過擬合[18]。

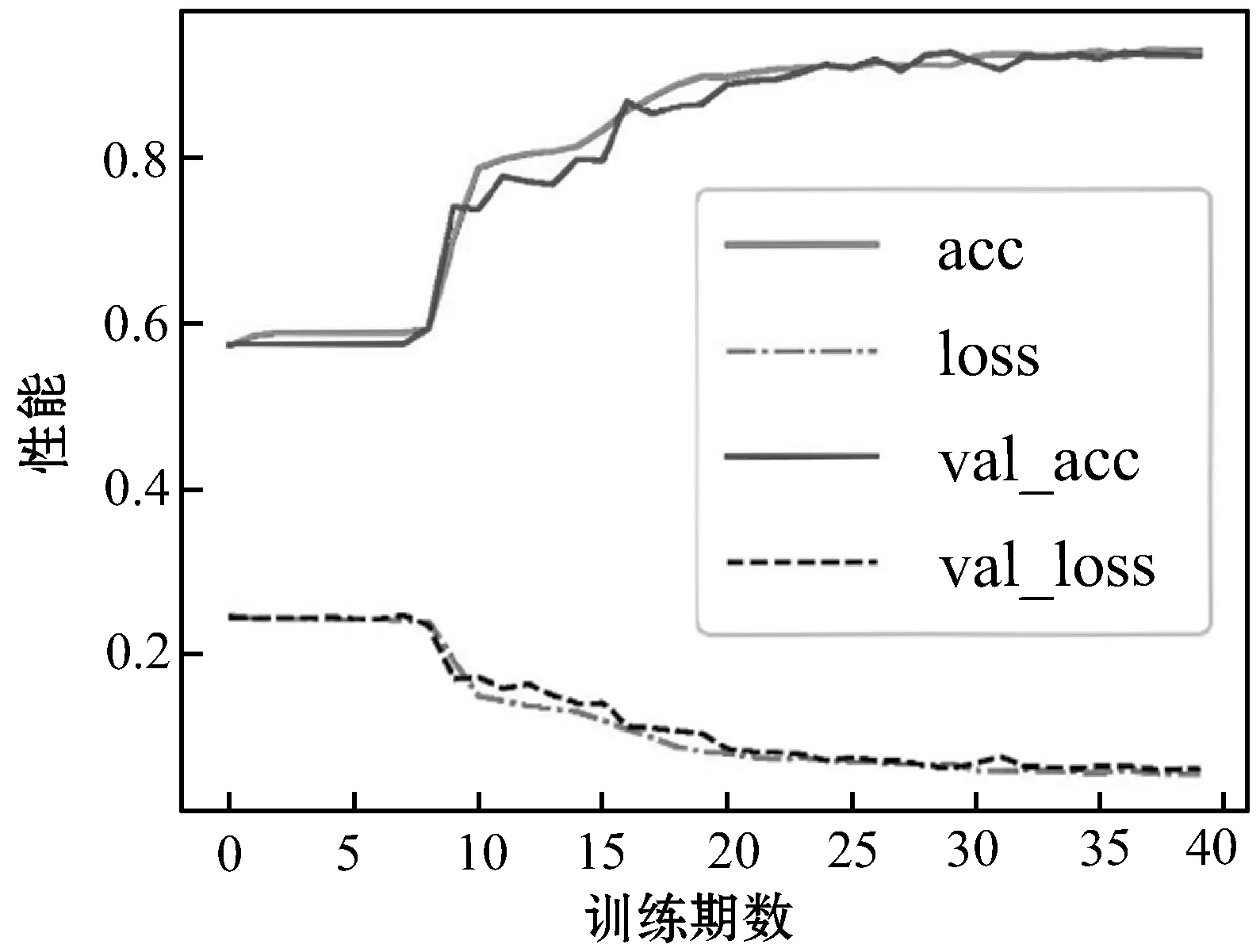
圖4 嚴重抑郁癥數據集上訓練和驗證過程的 準確度和損失率曲線

圖5顯示了分類器在嚴重抑郁癥數據集上進行抑郁癥篩選的ROC曲線，曲線是模型在嚴重抑郁癥數據集上的五折交叉驗證的每一折中所生成的。曲線的高AUC值(0.95以上)表明該分類器能夠有效地識別抑郁癥患者。

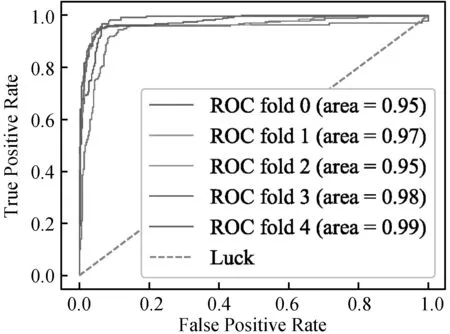
圖5 抑郁癥篩選的ROC 曲線

在同一數據集(MPHCs EEG數據[16])上，圖6顯示了該方法與基于多元logistic回歸分類器的小波(MLRW)的比較。直接分類準確率從87.5%提高到94.45%，靈敏度從95%提高到96.67%，特異性從提高80%到92.31%。相比于傳統非負矩陣分解算法，本文所提出的方法利用自編碼器刻畫動態注意力，同時分類準確率從90.23%提高到94.45%(基于本文所提出的多分支分類器)。

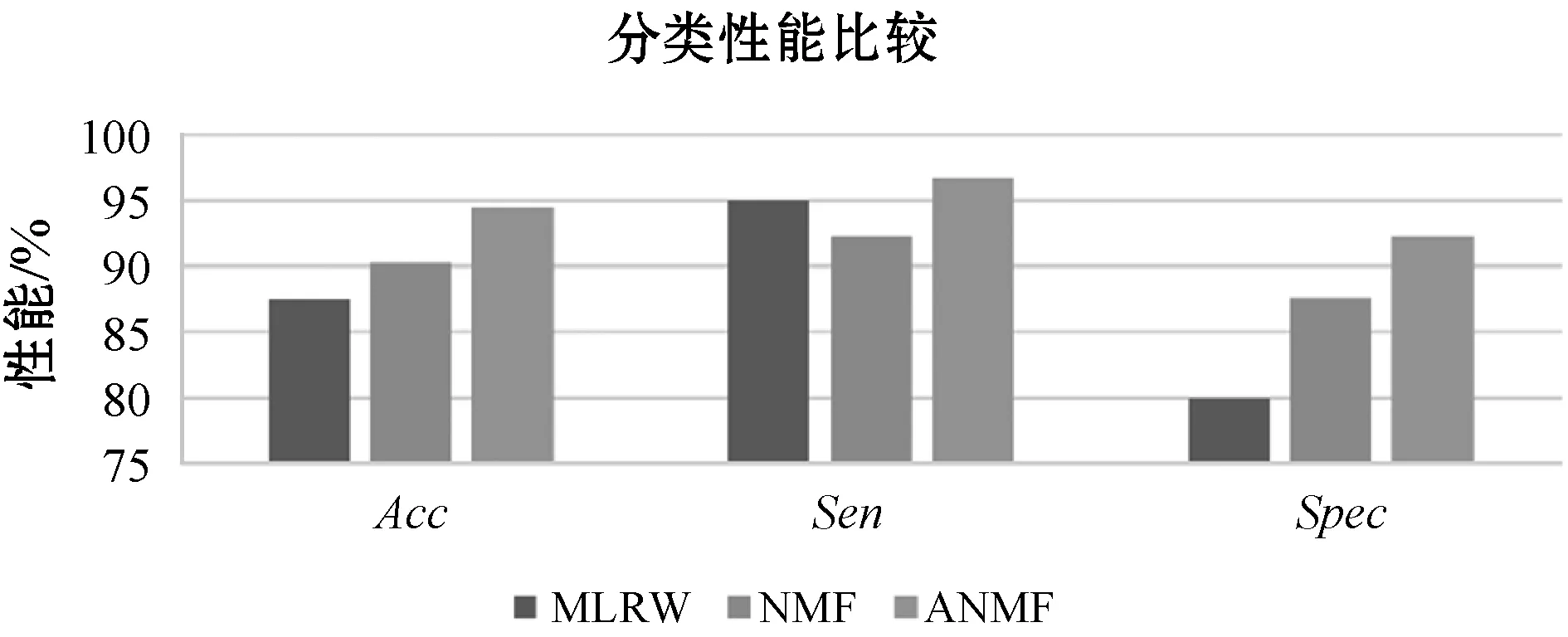
圖6 相關方法分類性能比較

3 結 語

針對現有非負矩陣分解方法在刻畫感興趣特征注意力方面存在不足，本文提出了一種基于注意力網絡的非負矩陣分解方法，在不需要任何特定先驗假設的情況下，將神經同步信號進行非負矩陣分解。之后，又設計了一個多路神經網絡，其充分利用了多路因子的結構信息，并且精確地從健康組中精確識別抑郁癥病人。

與最新的方法比較，所提出的方法在公開嚴重抑郁癥數據集上能夠獲得高分類精度：抑郁癥能分別以94.45%精確度、 96.47% 敏感度和92.31%特異度進行判別，超過了現有方法的分類性能(基于相同數據集)。此外， 通過自編碼器能動態自適應地提取神經數據同步特征的注意力。

綜上所述，本文使得同步特征的注意力分解成為可能。隱藏在復雜大腦神經數據中的注意力的提取有助于對腦狀態的識別。