基于摩擦自激振動理論的地鐵線路梯形軌枕支承小半徑曲線輪軌系統鋼軌波磨研究

崔曉璐 何志強 程 梽 楊宗超 楊宏光

(1.重慶交通大學機電與車輛工程學院， 400074， 重慶; 2.重慶市軌道交通(集團)有限公司， 401120， 重慶;3.中鐵物總運維科技有限公司， 100036， 北京; 4.中車長春軌道客車股份有限公司， 130062， 長春∥第一作者， 副教授)

0 引言

鋼軌波磨作為常見的軌道損傷問題之一，是鋼軌頂面沿縱向出現的一種規律性、似波浪狀的不平順磨損現象[1]。其產生的噪聲不僅對乘客的乘車舒適性造成極大影響，而且還會使車輛和軌道結構部件的使用壽命大為降低，極大增加了鐵路工務維修費用。目前，對于鐵路軌道上出現的鋼軌波磨問題尚未找到根本解決方法，但提出了一些相應的控制措施[2]。

現階段關于鋼軌波磨的成因，大致可分成以下兩種觀點[3]：①鋼軌頂面的粗糙度導致輪軌間瞬時動態接觸特性波動，進而產生波磨病害; ②輪軌間黏滑振動導致輪軌摩擦自激產生，進而導致摩擦功波動和相應的波磨病害。

軌道支承結構常被作為研究鋼軌波磨病害的重要對象。基于上述兩種理論，研究者們以軌道支承結構為著入點，開展了一系列的研究工作，并提出了相應緩解波磨病害的措施。文獻[4]從頻域角度出發，調查了北京地鐵隧道、橋梁上減振器扣件軌道結構上的鋼軌波磨問題，發現鋼軌波磨與扣件的剛度阻尼有關，通過優化扣件參數可以減緩鋼軌波磨的發展。文獻[5]基于固定波長機理，建立了非線性鋼軌波磨預測模型，發現降低軌墊剛度可以降低磨耗速率，緩解鋼軌波磨發展。文獻[6]利用頻域波磨模型，對影響鋼軌波磨的主要軌道支承結構參數進行了大量調查分析，發現軌枕質量、軌枕間距、軌墊橫向剛度、軌墊垂向剛度、道床垂向剛度對鋼軌波磨的影響較大，通過優化軌枕質量、軌枕間距、軌墊垂向剛度參數可以減緩鋼軌波磨發生趨勢。文獻[7]基于輪軌磨損理論與瞬態動力學的觀點，利用線性鋼軌波磨的預測模型,發現輪軌頂面的粗糙度與鋼軌波磨病害的產生緊密相關，導致波磨產生的直接原因是車輛軌道結構部分產生共振，通過采用連續的軌道支承結構能有效避免波磨病害。

本文基于摩擦自激振動理論研究某地鐵線路梯形軌枕支承小半徑曲線軌道上出現的波磨病害，通過對梯形軌枕支承小半徑曲線輪軌系統有限元模型的復特征值分析，研究了軌道減振結構中側向緩沖墊、底部橡膠墊板參數與扣件參數對輪軌摩擦自激振動發生趨勢的影響。同時，提出了相應的緩解波磨病害的措施。

1 地鐵梯形軌枕支承小半徑曲線輪軌系統仿真模型及理論方法

1.1 梯形軌枕支承小半徑曲線輪軌系統接觸模型

梯形軌枕是地鐵線路上常用的一種軌道支承結構，特別應用于對減振要求較高的路段。梯形軌枕軌道主要由鋼軌、扣件系統、連接鋼管、道床、側向緩沖墊、底部橡膠墊板和支撐塊組成[8]。側向緩沖墊和底部橡膠墊板作為道床與支撐塊之間的減振緩沖結構，又被統稱為軌道減振結構。

根據梯形軌枕支承小半徑曲線輪軌系統的結構形式，結合SIMPACK動力學仿真模型，建立梯形軌枕支承小半徑曲線輪軌系統的接觸模型，如圖1所示。通常而言，R(曲線半徑)≤350 m的曲線稱之為小半徑曲線[3]。當地鐵車輛通過梯形軌枕支承小半徑曲線軌道時，輪對兩端外側受到的垂向懸掛力和橫向懸掛力分別為FSVL和FSLL。輪對兩端內側受到的垂向懸掛力和橫向懸掛力分別為FSVR和FSLR。外輪法向力為NL，蠕滑力為FL；內輪法向力為NR，蠕滑力為FR[3]。扣件系統、側向緩沖墊和底部橡膠墊板利用接地彈簧和阻尼單元模擬。外輪、內輪與鋼軌間的接觸角分別為δL、δR。扣件的垂向剛度、垂向阻尼分別為KRV和CRV。軌道減振結構中側向緩沖墊的橫向剛度、橫向阻尼分別為KSL、CSL，底部橡膠墊板的垂向剛度、垂向阻尼分別為KSV、CSV。其中，KSL與KSV數值相同，CSL與CSV數值相同[8]。

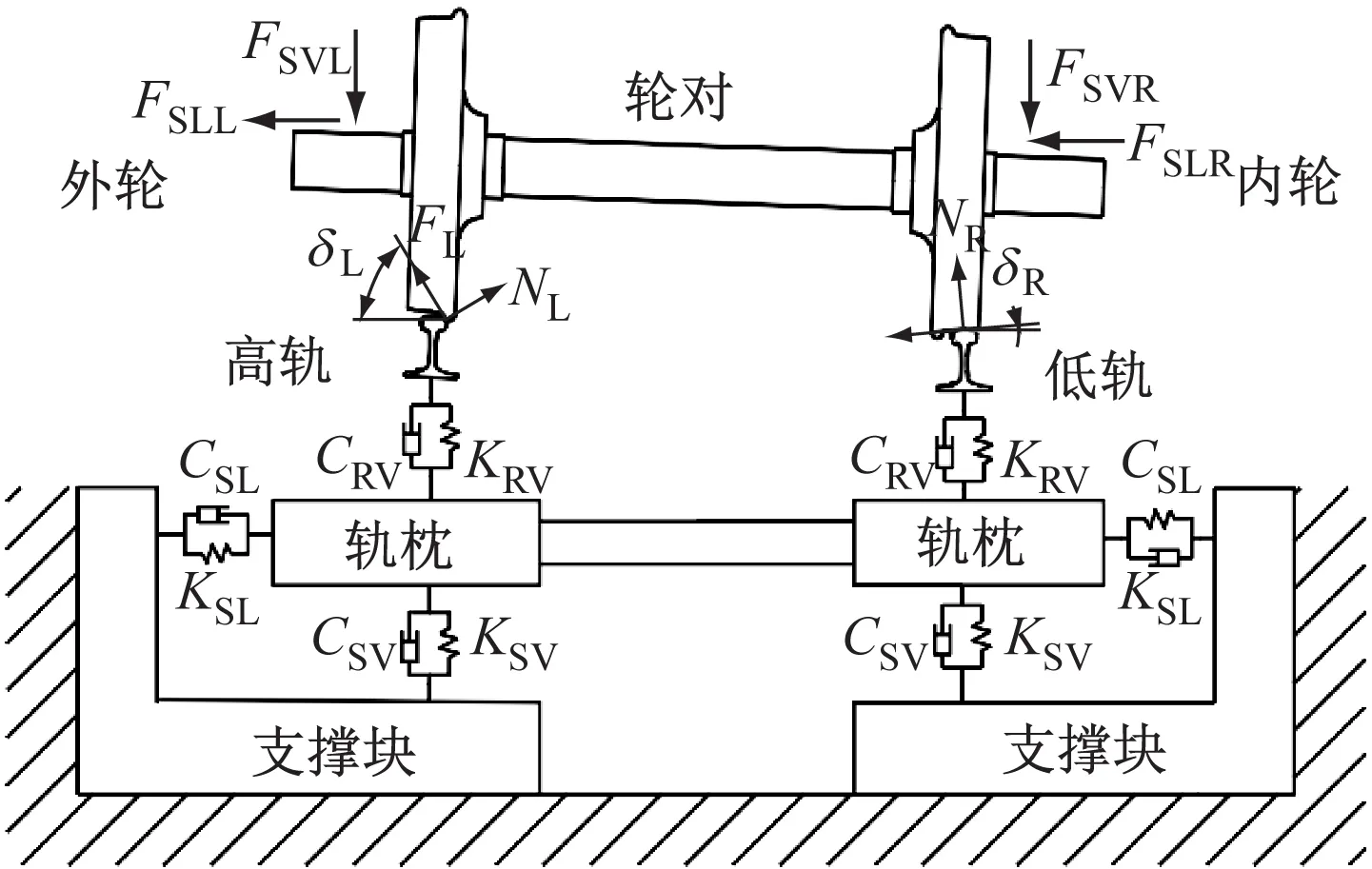
圖1 梯形軌枕支承小半徑曲線輪軌系統接觸模型Fig.1 Contact model of the wheel-rail on a sharp curved track supported by trapezoid sleepers

1.2 梯形軌枕支承小半徑曲線輪軌系統有限元模型

根據標準型梯形軌枕軌道結構以及輪軌接觸模型，利用ABAQUS有限元軟件建立梯形軌枕支承小半徑曲線輪軌系統的有限元模型，如圖2所示。

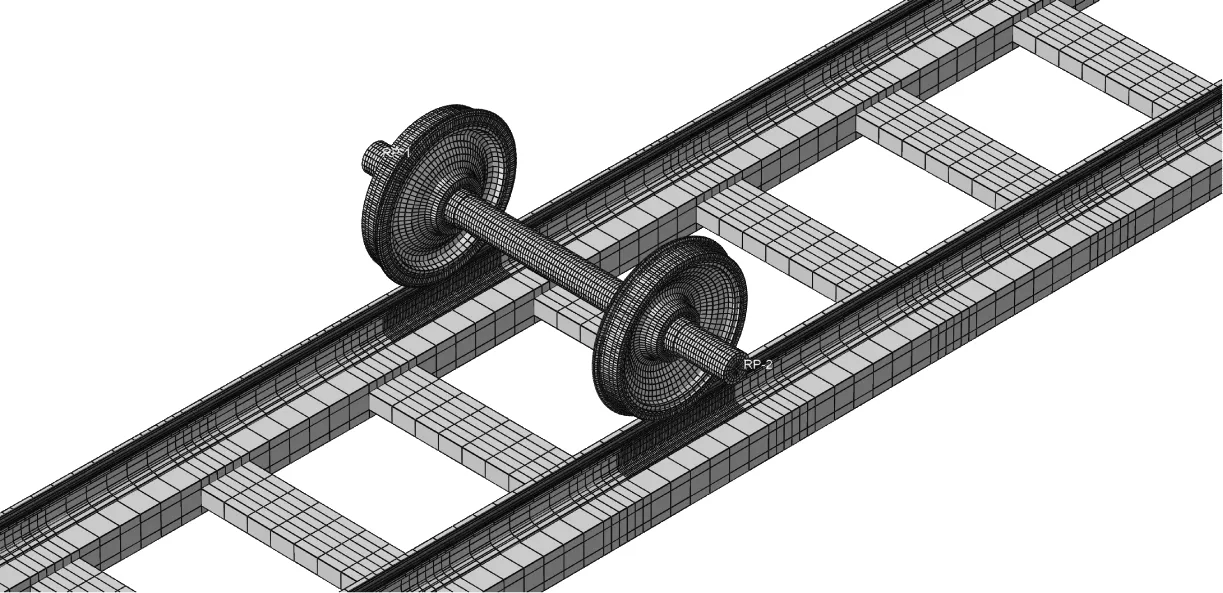
圖2 梯形軌枕支承小半徑曲線輪軌系統有限元模型Fig.2 Finite element model of the wheel-rail on a sharp curved track supported by trapezoid sleepers

該有限元模型中的各部件分別為輪對、鋼軌和軌道支承結構，其材料參數取值如表1所示[3]。

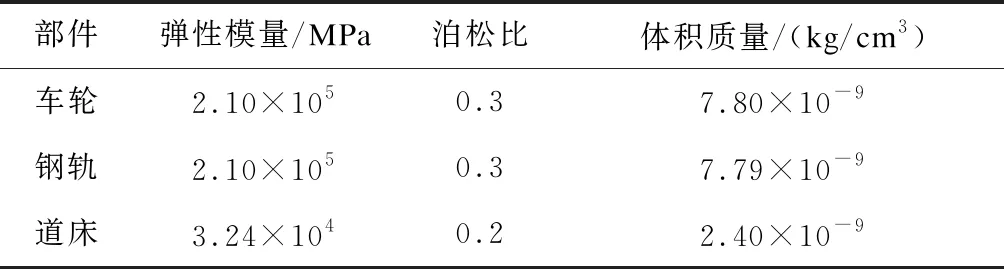
表1 梯形軌枕支承小半徑曲線輪軌系統各部件參數

模型中各部件尺寸為實際尺寸，采用固體單元模擬。由于導向輪對對波磨病害的影響最大，因此模型中的輪對特指導向輪對。鋼軌為長30 m的標準鋼軌，其兩端邊界設置為6個自由度全約束。輪對與鋼軌的接觸細節如圖3所示，輪軌摩擦系數設置為0.45。為了使模型計算結果更好收斂，需要對輪對與鋼軌接觸區域的網格作細化處理。在軌道支承結構中，扣件間距為625 mm，軌距為1 435 mm。扣件系統簡化為彈簧阻尼單元，由于單元數目眾多，因此采用Python腳本程序自動生成[3]。側向緩沖墊和底部橡膠墊板在軟件中利用點對面的形式直接設置生成。扣件系統與減振結構參數如表2所示[8]。本文主要研究梯形軌枕支承小半徑曲線軌道的固有特性，有限元模型中不考慮支撐塊以簡化計算。

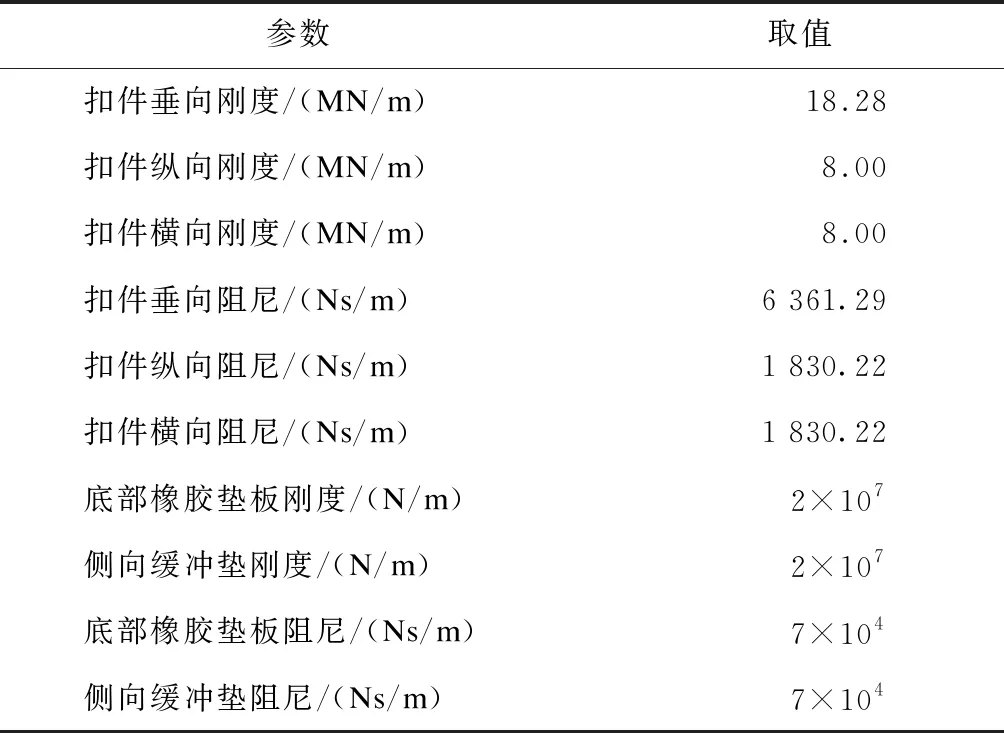
表2 梯形軌枕軌道支承結構參數

1.3 復特征值法

通過對梯形軌枕支承小半徑曲線輪軌系統發生摩擦自激振動時的振動頻率和相應的振動模態的提取，預測系統穩定性的方法稱為復特征值法[3]。建立不考慮摩擦和外力作用影響的運動微分方程：

(1)

式中：

x——節點位移向量；

M、C、K——分別為質量、阻尼、剛度矩陣,且均為對稱矩陣。

根據式(1)，可得到通解：

(2)

式中：

yk——第k階特征向量；

αk+jwk——第k階復特征值，其中，αk為特征值的實部，wk為特征值的虛部；

t——時間。

當αk>0時，輪軌系統可能會發生摩擦自激振動。

同時，通過引入評判摩擦自激振動發生趨勢的等效阻尼比ξk(ξk=-α/(π|wk|))亦可。當ξk為負值時，說明輪軌系統可能會發生摩擦自激振動，等效阻尼比越大，其發生的概率越小。

1.4 輪軌摩擦自激振動誘發波磨理論

通常鐵路領域認為輪對與鋼軌間的摩擦功波動是引發波磨病害的主要原因。文獻[9]提出的磨損公式如下：

w=K(H-C0)

(3)

式中：

w——單位時間內鋼軌頂面的磨損量；

K——磨損系數；

H——摩擦功(H為飽和蠕滑力F與相對速度v0的乘積)；

C0——耐久性摩擦功。

在小半徑曲線軌道上F將達到飽和狀態時，F為：

F=μN

(4)

式中：

μ——輪軌間的動摩擦系數；

N——輪軌間的法向接觸力。

根據式(4)可知，當輪軌系統發生摩擦自激振動時，輪軌間的摩擦功也出現了同頻率的振動，進而導致波磨病害的產生[3]。

1.5 輪軌系統的復特征值分析

根據前期調查和現場測試，在曲線半徑為300 m的梯形軌枕支承小半徑曲線軌道上，鋼軌波磨的情況十分嚴重，其波長主要集中在60～80 mm[10]，且主要發生在低軌上，而通過此路段地鐵車輛的運營速度約為80 km/h。根據頻率f、速度v和波長λ的關系式f=v/λ，可以求得波磨的頻率為277.8～463.0 Hz。

本文針對梯形軌枕支承小半徑曲線輪軌系統有限元模型進行復特征值分析，提取相應的摩擦自激振動模態和頻率，如圖4所示。

圖4 梯形軌枕支承小半徑曲線輪軌系統的等效阻尼比分布圖

由圖4可見，ξk分別為-0.013 430、-0.009 887、-0.023 590，其對應的頻率分別為156 Hz、230 Hz、337 Hz，說明梯形軌枕支承小半徑曲線輪軌系統存在3個摩擦自激振動頻率。其中，ξk是用于評判輪軌摩擦自激振動的重要參數。當梯形軌枕支承小半徑曲線輪軌系統的等效阻尼比為負數時，系統才可能會發生摩擦自激振動，且數值越小，系統發生摩擦自激振動的趨勢越大。因此可認為當ξk=-0.023 590時，此時輪軌系統發生摩擦自激振動的情況最容易出現，其對應的摩擦自激振動頻率為337 Hz。該頻率下對應的振動模態如圖5所示。由圖5可知，輪軌系統摩擦自激振動發生在低軌上。綜上所述，當輪軌系統振動頻率為337 Hz時，其會產生摩擦自激振動且發生在低軌上，從而可能誘導波長為66 mm的波磨，這與實際測試結果相符，進一步證明了誘導梯形軌枕支承小半徑曲線軌道上波磨病害的成因可能是輪軌間的摩擦自激振動。

圖5 梯形軌枕支承小半徑曲線輪軌系統的摩擦自激振動模態

2 軌道減振結構參數和總的扣件參數對輪軌摩擦自激振動的影響

2.1 軌道減振結構參數對輪軌摩擦自激振動的影響

在梯形軌枕支承小半徑曲線軌道支承結構中，梯形軌枕與支撐塊之間的底部橡膠墊板和側向緩沖墊是該軌道支承結構中減振降噪的主要部件。因此，軌道減振結構對于輪軌系統的振動具有重要影響[10]。采用參數化分析研究梯形軌枕支承小半徑曲線軌道減振結構中側向緩沖墊與底部橡膠墊板的結構參數呈倍數變化時對輪軌摩擦自激振動的影響。減振型軌道中減振結構的靜態剛度一般在8×106～4×107N/m范圍內，靜態阻尼一般在1.5×105Ns/m內[4]。在此范圍內，側向緩沖墊和底部橡膠墊板結構參數的變化情況如表3所示[8]。文獻[8]發現側向緩沖墊中縱向、垂向參數以及底部橡膠墊板中縱向、橫向參數對波磨病害幾乎沒有影響。

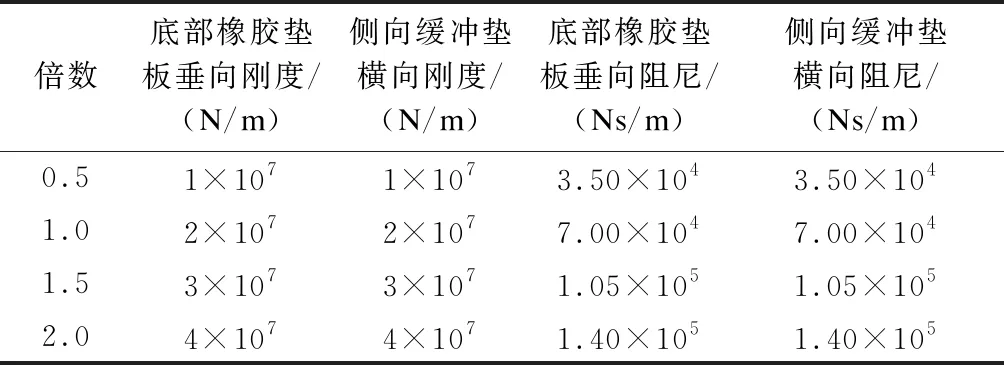
表3 減振結構參數隨其倍數變化值

利用復特征值法研究側向緩沖墊橫向剛度與阻尼、底部橡膠墊板垂向剛度與阻尼同時呈倍數變化時對輪軌摩擦自激振動頻率的影響，如圖6所示。由圖6可知，當側向緩沖墊和底部橡膠墊板的結構參數同時呈倍數變化時，輪軌系統的摩擦自激振動頻率始終保持在337 Hz。綜上可知，側向緩沖墊橫向剛度與阻尼、底部橡膠墊板垂向剛度與阻尼同時呈倍數變化時，對輪軌系統的摩擦自激振動頻率基本沒有影響。

圖6 軌道減振結構參數-輪軌摩擦自激振動頻率關系曲線

圖7為側向緩沖墊的橫向剛度、橫向阻尼呈倍數變化時對輪軌摩擦自激振動發生趨勢的影響。由圖7 a)可知，隨著側向緩沖墊橫向剛度的增加，等效阻尼比變化幅度不大，說明側向緩沖墊橫向剛度對輪軌摩擦自激振動發生趨勢影響很小。由圖7 b)可知，隨著側向緩沖墊橫向阻尼的增加，等效阻尼比基本不變，說明側向緩沖墊橫向阻尼的變化對輪軌摩擦自激振動發生趨勢的影響也很小。

a) 側向緩沖墊橫向剛度

b) 側向緩沖墊橫向阻尼圖7 側向緩沖墊參數-等效阻尼比關系曲線Fig.7 Relationship curve of parameters of the lateral cushion and equivalent damping ratio

圖8為底部橡膠墊板的垂向剛度、垂向阻尼呈倍數變化時對輪軌摩擦自激振動發生趨勢的影響。由圖8 a)可見，隨著底部橡膠墊板垂向剛度的增加，摩擦自激振動的等效阻尼比呈增大趨勢，但增幅極小。由圖8 b)可見，隨著底部橡膠墊板垂向阻尼的增大，等效阻尼比越大，即輪軌摩擦自激振動的發生趨勢就越小。綜上所述，軌道減振結構中側向緩沖墊參數對輪軌摩擦自激振動的發生趨勢影響不大，所以通過增大其橫向剛度降低摩擦自激振動發生趨勢的意義不大。而底部橡膠墊板中垂向阻尼對摩擦自激振動發生趨勢有較大的影響，在一定范圍內通過增加底部橡膠墊板的垂向阻尼，有助于降低輪軌摩擦自激振動的發生趨勢，當底部橡膠墊板中垂向阻尼接近于1.5×105Ns/m時，輪軌系統最不易發生摩擦自激振動。

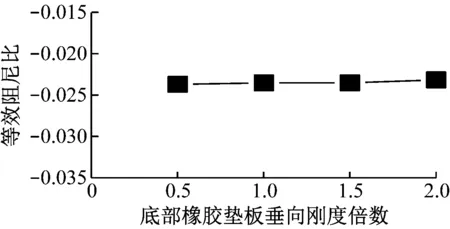
a) 底部橡膠墊板垂向剛度

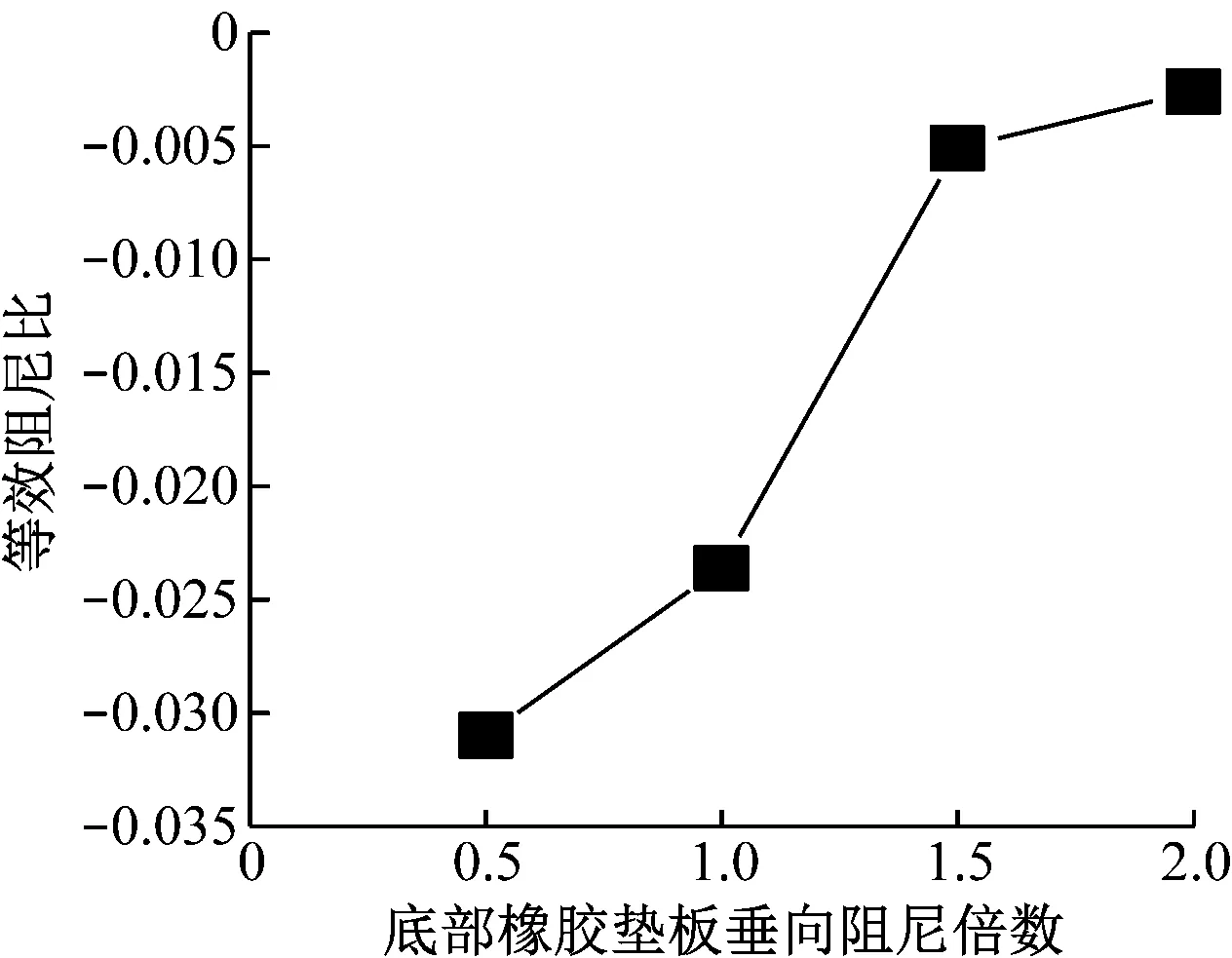
b) 底部橡膠墊板垂向阻尼圖8 底部橡膠墊板參數-等效阻尼比關系曲線Fig.8 Relationship curve of parameters of the bottom rubber pad and equivalent damping ratio

2.2 總的扣件參數對輪軌摩擦自激振動的影響

文獻[11-12]驗證了軌道支承結構中扣件參數對波磨病害的影響較為明顯。本文采用參數化分析討論總的扣件參數呈倍數變化時對輪軌摩擦自激振動發生趨勢的影響。

現階段，國內城市軌道結構使用的扣件靜態剛度一般在5～60 MN/m，靜態阻尼一般小于1.5×105Ns /m[3]。在此范圍內，扣件參數的變化如表4所示[11]。采用復特征值法研究不同扣件參數對梯形軌枕輪軌摩擦自激振動發生趨勢的影響，如圖9～10所示。

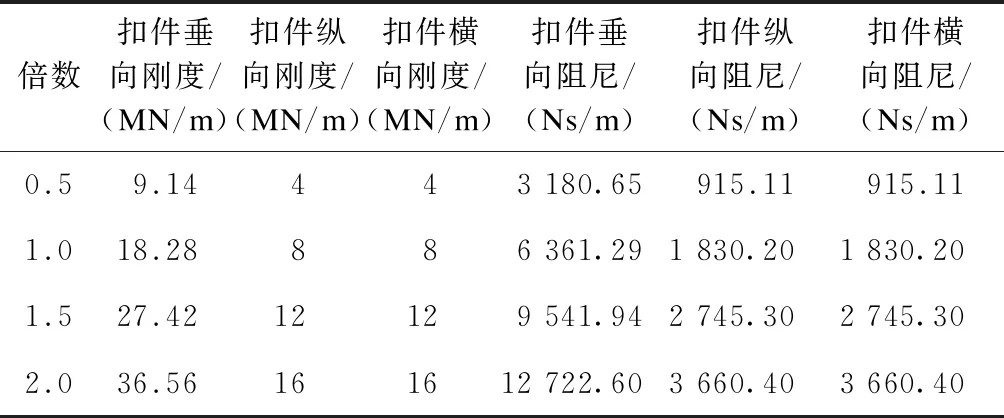
表4 扣件參數隨其倍數變化值

由圖9可見，隨著總的扣件剛度的增大，即扣件的垂向、橫向、縱向剛度均增大時，輪軌系統的負等效阻尼比增大，即發生摩擦自激振動的趨勢降低。因此，通過增加總的扣件剛度有助于降低輪軌系統摩擦自激振動的發生趨勢，即當總的扣件剛度接近60 MN/m時，輪軌系統最不易發生摩擦自激振動。

圖9 總的扣件剛度-等效阻尼比關系曲線Fig.9 Relationship curve of overall fastener stiffness and equivalent damping ratio

圖10 總的扣件阻尼-等效阻尼比關系曲線Fig.10 Relationship curve of overall fastener damping and equivalent damping ratio

由圖10可知，隨著總的扣件阻尼(即扣件垂向、橫向、縱向阻尼)的增大，輪軌系統負的等效阻尼比基本不變，即輪軌系統發生摩擦自激振動的趨勢基本不變。因此，通過調整總的扣件阻尼以降低摩擦自激振動的發生趨勢意義不大。基于摩擦自激振動的觀點，在一定范圍內，通過改變總的扣件剛度對產生自激振動的等效阻尼比影響較大，而總的扣件阻尼變化對等效阻尼比的影響較小。由此可見，通過增加總的扣件剛度有助于緩解輪軌系統摩擦自激振動的發生趨勢。

3 結論

1) 在梯形軌枕支承小半徑曲線軌道上，使輪軌系統發生摩擦自激振動的頻率為337 Hz且主要發生在低軌上，在該頻率下可能會誘發波長為66 mm的波磨。

2) 在軌道減振結構參數對輪軌摩擦自激振動的影響研究中，減振結構參數的改變對該區段輪軌摩擦自激振動的誘導頻率的影響較小，而減振結構參數對輪軌摩擦自激振動的發生趨勢的影響較為明顯。在一定范圍內通過增加減振結構中底部橡膠墊板的垂向阻尼，可以有效降低摩擦自激振動發生的趨勢，從而有助于減緩相應區段的波磨病害。

3) 在一定范圍內通過改變扣件參數，發現總的扣件剛度對輪軌系統摩擦自激振動的發生趨勢影響較大，而總的扣件阻尼對輪軌摩擦自激振動的發生趨勢影響較小。通過增加總的扣件剛度有助于減緩相應區段內的波磨病害。