局部振動壓實荷載對地鐵車站結構開裂影響分析*

魏度強 余 超 張慧鵬 夏 明 石鈺鋒

(1.中國鐵路南昌局集團有限公司， 330009, 南昌； 2.佛山市鐵路投資建設集團有限公司， 528041, 佛山；3.南昌軌道交通集團有限公司， 330038, 南昌； 4.華東交通大學土木工程國家實驗教學示范中心， 330013,南昌∥第一作者， 助理工程師)

我國地鐵建設快速發展的同時，其質量也越來越受到重視。地鐵結構質量好壞直接關系到其自身的運營安全、使用壽命乃至周邊環境[1],因此，嚴格控制車站主體結構變形、開裂等現象變得愈來愈重要。

目前，文獻[2-6]分析了不同施工階段、溫度及收縮效應等因素對地鐵車站結構裂縫的影響，而針對局部蓋挖法施工中，由于回填施工順序不同造成局部振動壓實作用下產生的不均勻沉降而導致其開裂的現象鮮有討論。

本文將在前期靜力分析[7-8]的基礎上，通過動力分析，研究在不同振動頻率、名義振幅及振動次數下局部振動壓實荷載對車站結構開裂的影響程度及其規律。

1 某地鐵車站結構裂縫分布特征

1.1 工程概況

某地鐵車站(見圖1)總長206.1 m，標準段寬21.7 m，車站頂板覆土厚3.0～3.5 m。車站主體結構采用明挖順作法(局部蓋挖法)施工，共分3期：

1) 第1期：施工便橋區車站圍護結構及便橋(便橋搭建于圍護結構及其下方的混凝土橫撐上)，以恢復路面交通。

2) 第2期：施工車站其余區域的圍護結構，然后進行基坑開挖及主體施做、頂板回填(回填分區為先便橋兩側，后便橋區)。

3) 第3期：施工車站附屬結構。

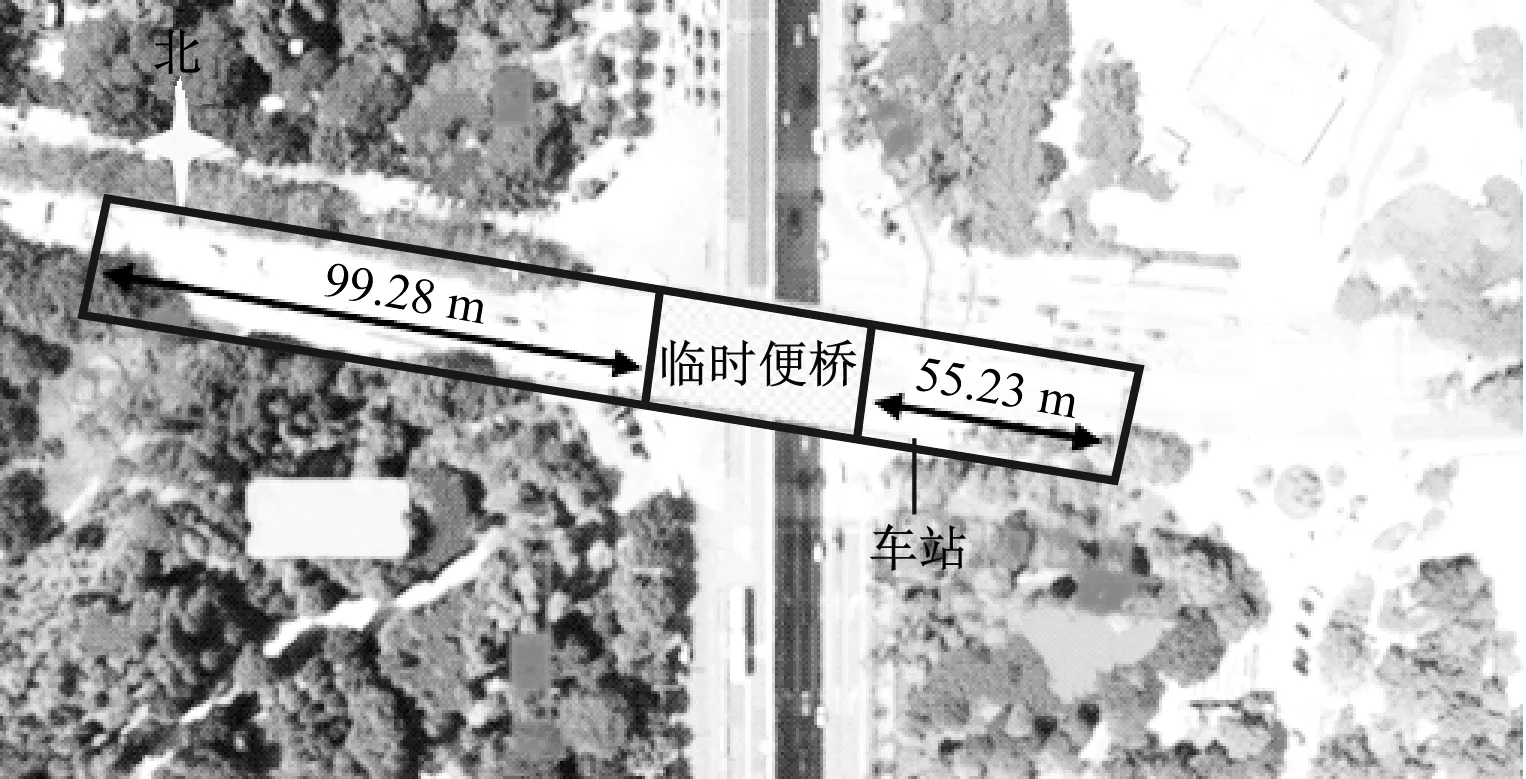
圖1 某地鐵車站平面位置圖Fig.1 Location plan of certain metro station

便橋與車站主體結構的位置關系見圖2。車站結構標準斷面見圖3。

車站回填采用殘積砂質黏性土，分層回填(每層厚0.5 m)并碾壓。其中，車站1～12軸范圍內共回填7層，18～24軸范圍內共回填6層。

a) 橫剖面

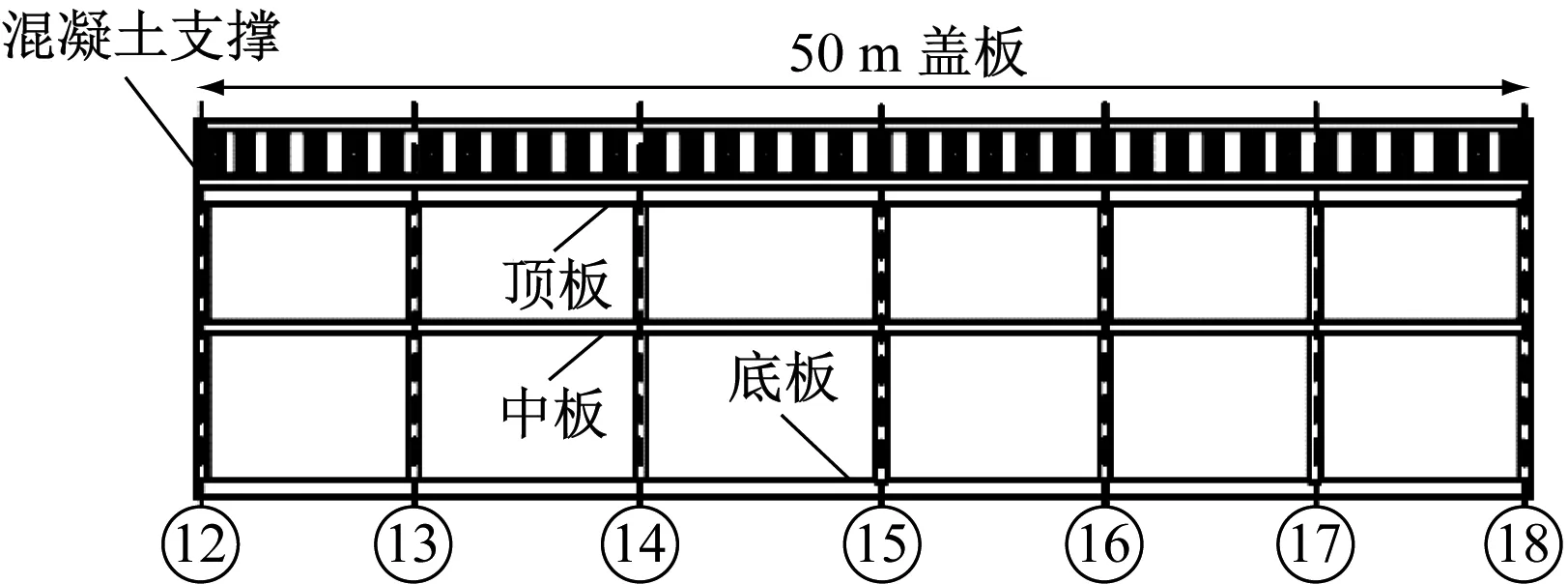
b) 縱剖面圖2 地鐵車站結構與便橋的位置關系圖Fig.2 Location relation of metro station structure and temporary bridge

車站范圍內的土層依次為素填土、粉質黏土、殘積砂質黏性土、全風化花崗巖、散體狀強風化花崗巖(見圖3)。車站底板主要坐落于全風化花崗巖上，該土層具有軟化性與崩解性，擾動后強度損失大，遇水后易崩解。

1.2 車站結構裂縫分布特征

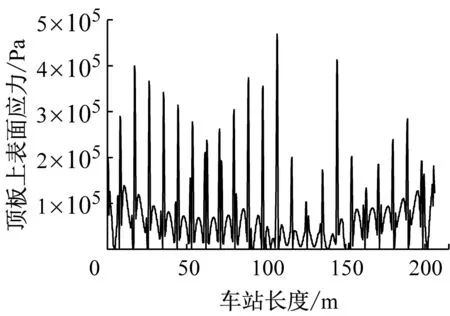
蓋板下方頂板混凝土澆筑完成后4個月，便橋兩側進行土體回填。回填后，便橋下方車站頂板及側墻區域混凝土結構產生裂縫。車站結構裂縫平面展布圖如圖4所示。

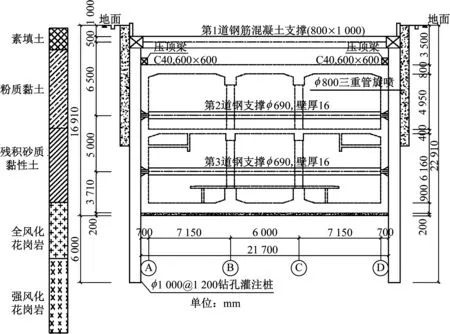
圖3 地鐵車站結構標準斷面圖Fig.3 Standard section of metro station structure

圖4 地鐵車站結構裂縫平面展布示意圖Fig.4 Schematic diagram of plane distribution of metro station structure cracking

由圖4可知，車站頂板裂縫主要發生在11～12軸頂板與縱梁之間及13～18軸整塊頂板區域，各裂縫間距約2 m，寬度為0.02～0.10 mm，為上下貫穿型裂縫。

通過對實際工程進行分析，發現中板、站臺層側墻和頂板、站廳層側墻均采取側墻與板整體澆注的施工方法進行澆筑，澆筑后經檢驗各板、墻混凝土性質較穩定且差異性小；站廳層頂板及側墻各部分混凝土強度質量均合格，且裂縫僅在11～18軸范圍內發生，其余軸線范圍內均無裂縫產生。根據文獻[7-8]，該地鐵車站結構開裂是由不均勻回填荷載、坑底全風化花崗巖擾動后未處理及壓路機振動等綜合因素引起的。

2 地鐵車站有限元模型的建立

2.1 模型的建立與邊界條件的設置

本文通過ABAQUS有限元軟件建立車站-土體二維模型(見圖5)，模型長500 m、高100 m，對此車站結構進行動力分析。

圖5 地鐵車站-土體二維有限元模型圖Fig.5 Two dimensional finite element model of metro station-soil

考慮到初始靜應力條件，地鐵車站-土體二維有限元模型計算從靜力分析步過渡到動力分析步時，須對模型地基的側向邊界條件進行轉換。

土體-地下結構靜、動力耦合邊界的處理技術主要有兩種：一種是文獻[9]提出的靜-動力統一人工邊界技術；另一種是靜-動力耦合邊界處理技術。靜-動力耦合邊界處理技術是在靜力分析步中，在其側向邊界采用水平向約束和豎向自由的滾軸邊界；在動力分析步中，在其側向邊界采用水平向自由和豎向約束的滾軸邊界；在靜力分析步向動力分析步轉化的過程中，將靜力分析結束后側向邊界的水平向支座反力采用人工方式以集中力施加于側向邊界上的靜力水平支座對應的單元結點上，以此來實現靜力邊界條件向動力邊界條件的轉化，具體轉化過程見圖6。

圖6 分析步中靜、動力邊界條件轉換

由于第2種方法概念明確且實施容易，因此，本文中對靜、動力耦合作用下車站主體結構側向邊界的處理采用第2種方法。

2.2 車站-土體模型本構關系與參數的選擇

采用摩爾-庫侖本構模型及NewMark-β法研究局部振動壓實荷載作用對地鐵車站的影響規律。土體采用Rayleigh阻尼，地下連續墻、車站梁-柱及樓板結構采用線彈性本構。根據模態求得的固有頻率對該模型進行有限元計算。地鐵車站-土體二維有限元模型所選參數見表1～2。

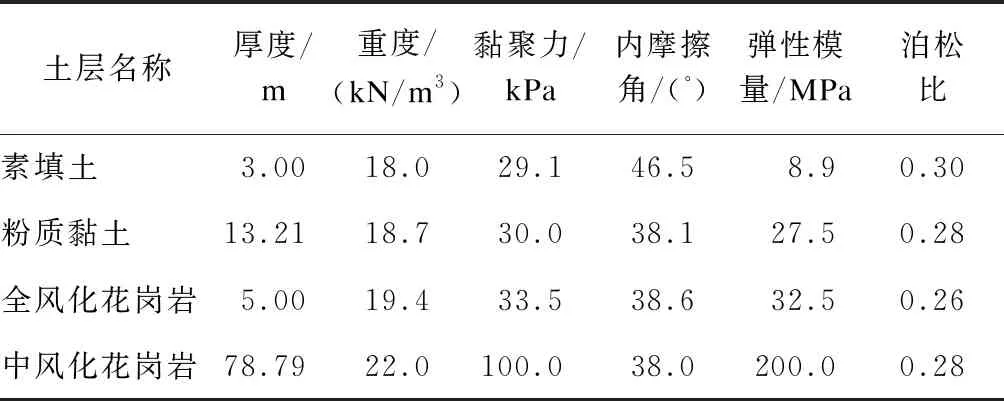
表1 某地鐵車站土層物理力學參數表

表2 某地鐵車站結構設計參數

2.3 振動壓路機荷載

振動壓路機的振動參數主要由其參振質量md、振動頻率f與名義振幅A0決定[10]。由于振動壓路機的工作振幅是一個隨機參數，為便于評價和比較不同機型振動壓路機的振動性能，引入了“名義振幅”概念。表3為實際工程中所用的振動壓路機參數。當已知振動壓路機的參振質量md、振動頻率f與名義振幅A0時，壓路機激振力F0的計算公式為：

F0=mdA0(2πf)2

(1)

表3 振動壓路機參數表

2.4 模擬工序

1) 對車站結構及周圍土體進行初始地應力計算；

2) 施加靜荷載模擬不同區域土體的回填；

3) 對基坑不同區域分步施加如圖7所示的動力荷載,模擬振動壓路機振動壓實過程。

圖7 壓路機荷載模型Fig.7 Load model of road roller

3 地鐵車站模擬數據與監測數據對比

車站施工過程中的監測內容主要包括：①圍護樁頂水平位移監測；②圍護樁頂豎向位移監測；③圍護樁水平位移監測；④地表沉降監測；⑤基坑底部沉降監測。車站基坑監測點平面布置圖見圖8。

圖8 地鐵車站基坑監測點平面布置圖

由于本次模擬未考慮基坑開挖過程，僅考慮土體回填過程對地鐵車站的影響，故監測數據僅選取了基坑底部ZCZ-1、ZCZ-2、ZCZ-3 3點。選取2016年11月基坑開挖完成至2018年1月蓋挖區兩側土體回填完成期間基坑底部標高變化量進行對比分析。

圖9為車站基坑現場監測數據、靜力分析與動力分析結果對比曲線。由圖9可知，使用振動壓路機對蓋板兩側土體回填并壓實的過程中，地鐵車站主體結構會發生較大的不均勻沉降。不論是靜力分析[10-11]還是動力分析，車站基坑底部的整體沉降均與實際監測數據吻合，采用靜力分析法得到的數據可能會偏大，動力分析法得出的數據與實測數據較為接近。這表明本文所采用的動力分析法數值模擬是可行的,且較之靜力分析更為合理。

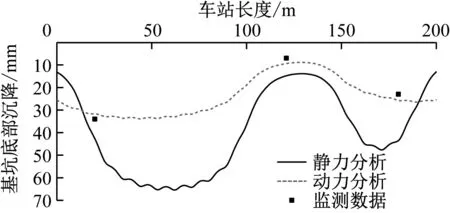
圖9 地鐵車站基坑底部模擬數據與監測數據對比

4 不同振動壓實荷載對地鐵車站結構的影響

4.1 振動壓路機振動次數對地鐵車站的影響

為研究振動壓路機振動次數對地鐵車站結構開裂的影響，選取表4所示的4種工況，對車站頂板上表面應力分布及基坑底部最大沉降差進行分析。

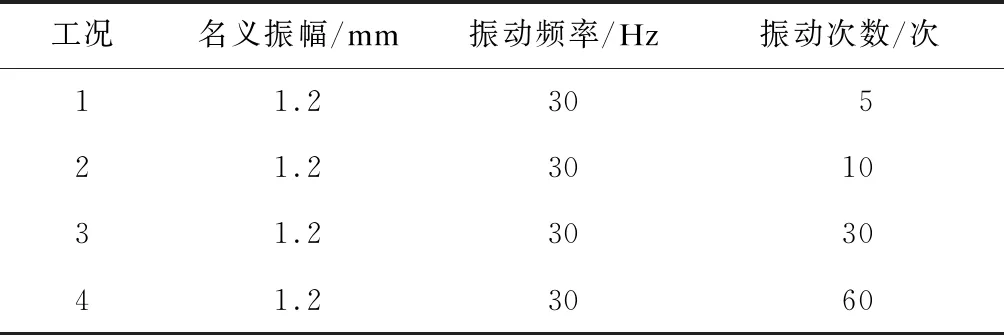
表4 不同振動次數工況表

如圖10所示，振動壓路機振動次數所引起的地鐵車站上表面應力分布情況是一致的，但是隨著振動次數的增加，車站頂板上表面最大應力會呈現先增加后減小的趨勢。

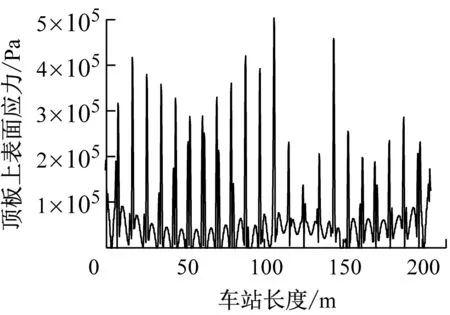
a) 工況1

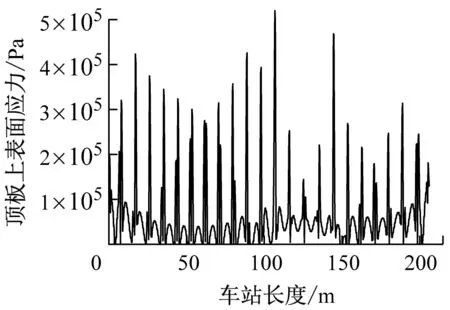
b) 工況2

c) 工況3

d) 工況4

由表5所示，振動壓路機振動30次時，基坑底部土體最大沉降差值達到最大，而振動60次時土體的沉降差反而降低到比振動5次時的數值還小。這可能是由于土體較為松散時，隨著振動次數的增加，土體以塑性變形為主，且其變形量較大；而隨著土體密實度的提高，土體塑性變形量減小，且振動次數的增加對土體變形量影響較小。

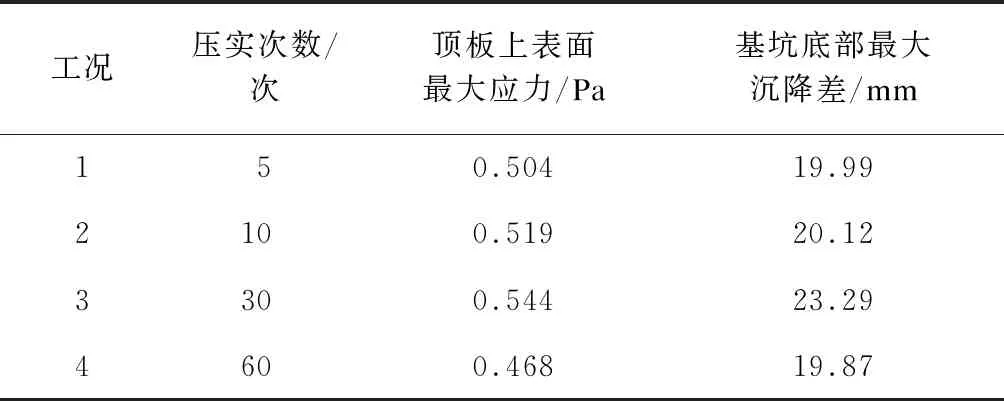
表5 不同壓實次數下車站頂板上表面最大應力和基坑底部最大沉降差

4.2 振動壓路機名義振幅對地鐵車站的影響

如表6所示，選取1.2 mm、1.5 mm、1.8 mm等3種不同名義振幅，分別在振動頻率為30 Hz，振動次數為5、10、30、60次的條件下，研究名義振幅對地鐵車站的影響。

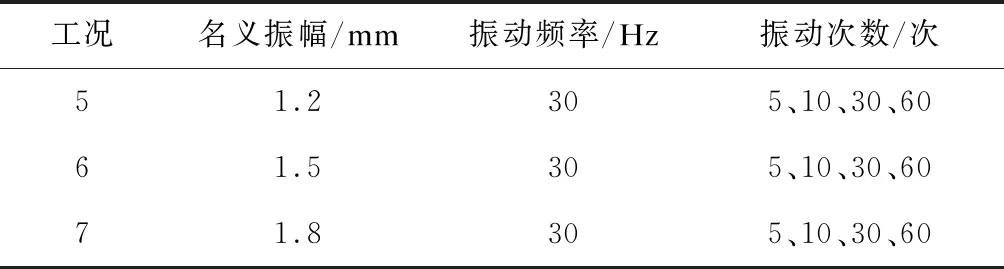
表6 不同名義振幅工況表

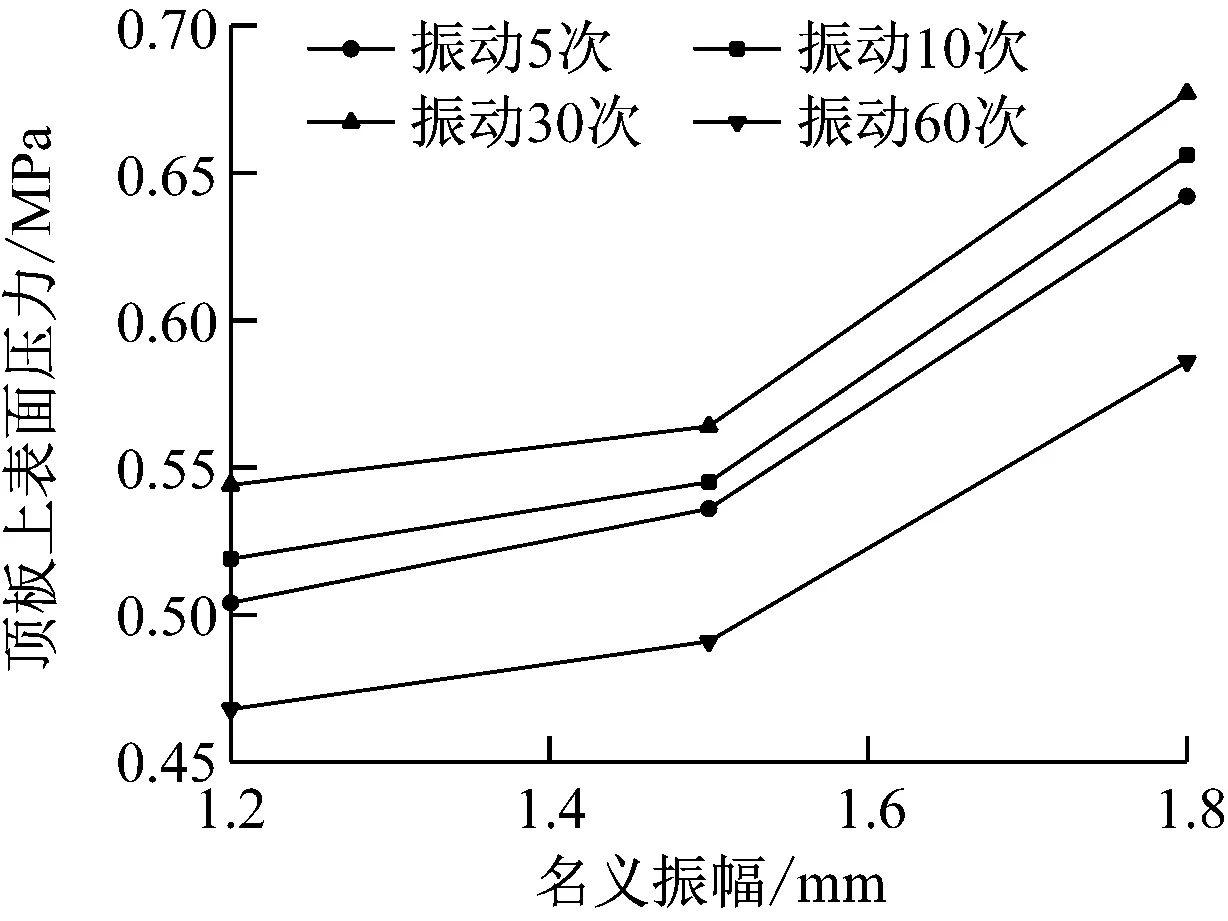
由圖11 a)可知，車站頂板上表面最大應力值隨著名義振幅的增大而逐漸增加；當名義幅值為1.2 mm時，振動壓路機振動5次造成的最大應力值約為0.519 MPa；當名義幅值為1.5 mm時，頂板上表面最大應力值約為0.545 MPa，僅比名義幅值為1.2 mm時增加了約4.7%；而名義幅值為1.8 mm時，車站頂板最大應力值達到了0.656 MPa，較名義振幅為1.2 mm時增幅高達26.3%。

由圖11 b)可知，除振動30次外，在名義振幅為1.2 mm時，振動5、10、60次時的基坑底部土體最大沉降差較為接近，均接近20 mm。但隨著名義振幅的增加，不同振動次數下基坑底部的最大沉降差變化規律相差較大。振動次數為30次時，隨著名義振幅的增加，基坑底部的最大沉降差呈現出較大的增長，從名義振幅為1.2 mm時的23.28 mm增加到名義振幅為1.8 mm時的41.48 mm，增幅接近1倍；而當振動次數為60次時，隨著名義振幅的增加，基坑底部最大沉降差值變化不大，僅由名義振幅為1.2 mm時的19.87 mm增加到名義振幅為1.8 mm時的21.05 mm。

a) 頂板上表面最大應力

b) 基坑底部最大沉降差

4.3 振動壓路機振動頻率對地鐵車站的影響

如表7所示，選取2 Hz、5 Hz、10 Hz、20 Hz、30 Hz等5種不同振動頻率，分別在名義振幅為1.2 mm，振動次數為5、10、30、60次的條件下，研究不同振動頻率對地鐵車站的影響。

表7 不同振動頻率工況表

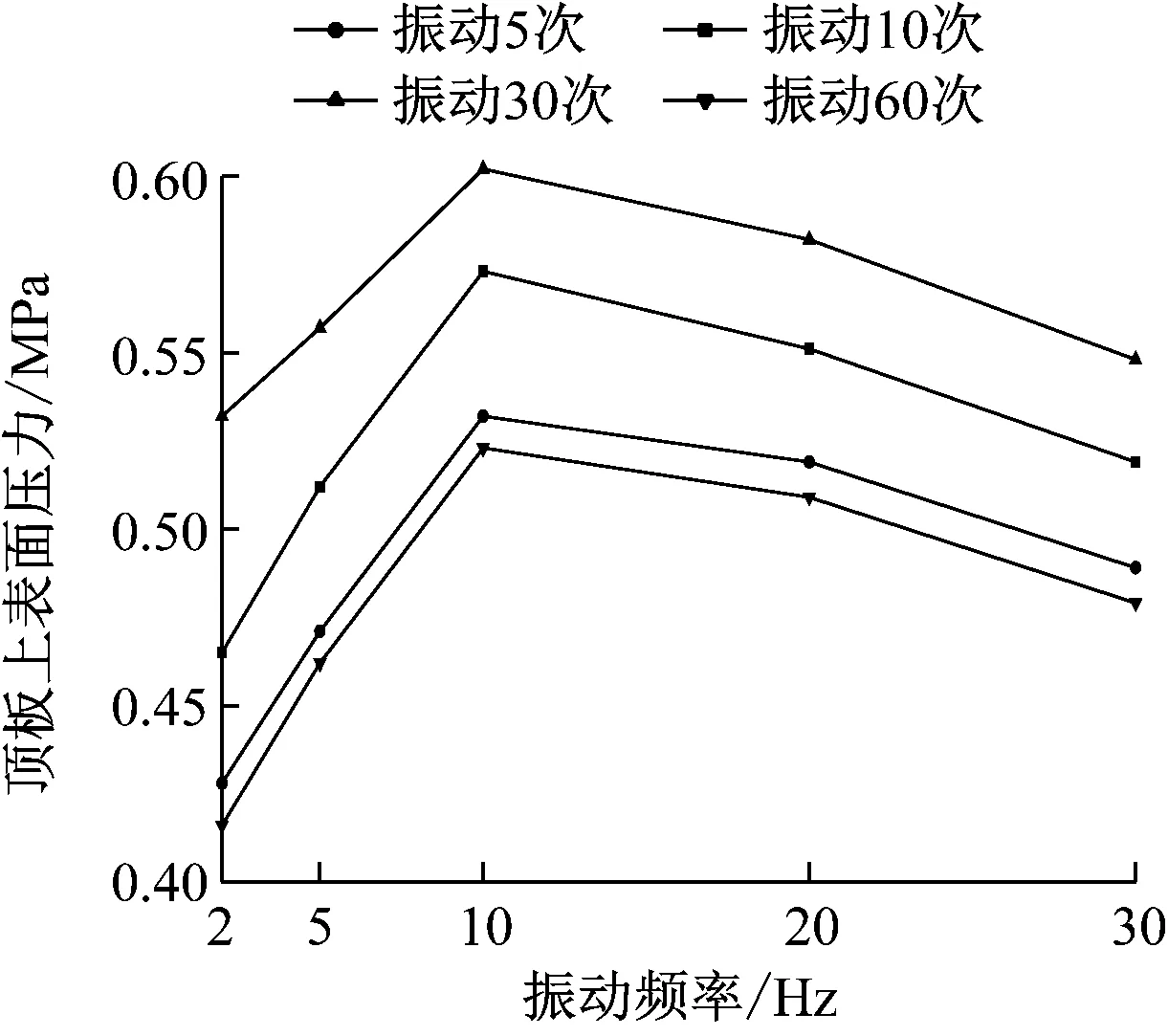
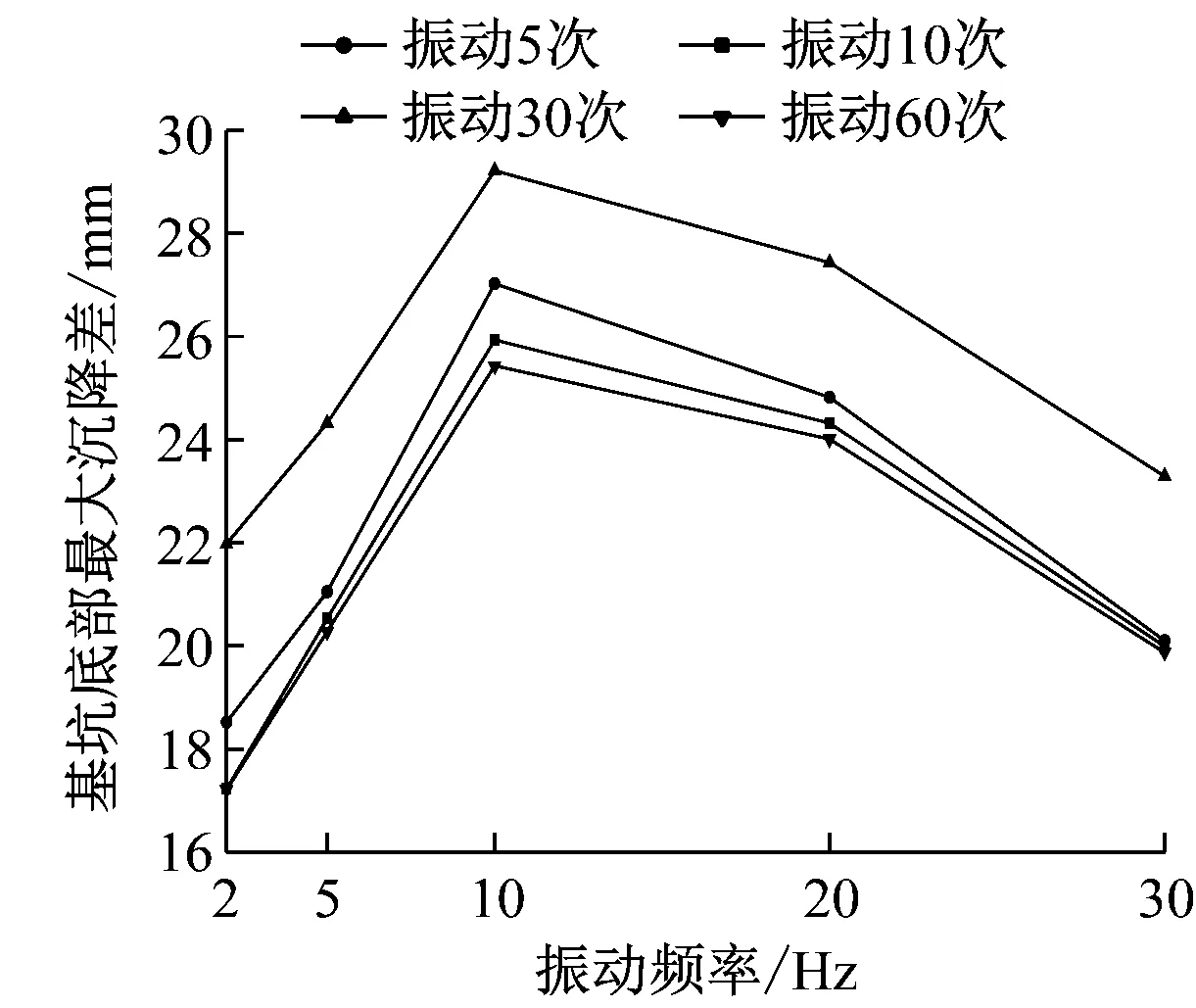
由圖12可知，隨著振動頻率的增加，地鐵車站頂板上表面最大應力值與基坑底部最大沉降差值均呈現先增加后減小的趨勢；當振動頻率為10 Hz時，車站頂板上表面最大應力約是振動頻率為2 Hz時的1.25倍，而基坑底部土體最大沉降差值約是振動頻率為2 Hz時的1.5倍。

a) 頂板上表面最大應力

b) 基坑底部最大沉降差

由此可見，該基坑底部土體存在一個合適的共振頻率范圍，在此共振頻率范圍內，土體會得到充分壓實使得沉降差擴大，從而導致車站頂板上表面拉應力增加產生開裂；而當基坑底部土體超過該頻率后，由于土體過于密實其相對沉降差會減小，車站頂板上表面拉應力亦會隨之減弱。

5 結論

1) 靜力模擬和動力模擬整體趨勢類似并與監測數據吻合，但靜力模擬數據明顯偏大，而動力分析更為準確。

2) 對振動壓路機振動壓實荷載影響較大的主要是其名義振幅與振動頻率，振動次數對基坑底部沉降差的影響較小。

3) 當土體比較松散時，在振動壓路機振動碾壓下，基坑底部土體的變形量較大，且其隨著壓實次數的增加而逐漸增大；而隨著土體密實度的提高，土體在振動壓實下變得更為密實，基坑底部沉降量會隨著壓實次數的增加而降低。

4) 振動次數與振動頻率的增加均會使得基坑底部最大沉降差呈現先增大后減小的趨勢，而最大沉降差會隨著名義振幅的增加而增大。

5) 當振動壓路機振動頻率為10 Hz、名義振幅為1.8 mm時，土體最大沉降差值最大，使局部蓋挖后填區車站主體結構產生應力集中，承受較大拉應力，可能使得頂板發生開裂。