城市軌道交通站臺客流聚集模型研究

肖 颯 蒲 琪

(同濟大學鐵道與城市軌道交通研究院， 201804， 上海∥第一作者，碩士研究生)

城市軌道交通換乘車站相較于非換乘車站更易形成大客流聚集，準確計算換乘車站站臺最高聚集人數可為站臺客流壓力評估提供重要的基礎數據。目前，對于換乘車站站臺聚集人數的研究還處于初級階段。文獻[1]在文獻[2]的基礎上，將換乘客流視為周期性進入站臺，在兩線列車到達間隔時間相同且恒定的條件下，得到了單側線路客流在站臺的最高聚集人數的方法。大多數學者建立換乘站站臺聚集人數模型的技術路線為：將站臺客流分為上車客流和下車客流，假定進入站臺的上車客流為均勻分布、列車到達時間間隔恒定、不考慮滯留乘客，在這些前提條件下獲得站臺最高聚集人數。但大部分模型中并未考慮滯留乘客的影響，換乘線路發車間隔對聚集人數模型的影響亦還未考慮。

1 換乘車站站臺聚集人數模型研究條件設定

1.1 客流分析

將客流劃分為上車客流和下車客流；將進站客流劃分為進站上車客流、換乘上車客流和滯留客流；將下車客流劃分為換乘客流和出站客流，兩者可合并為下車客流一并研究。本文將乘客進站、出站、上車、下車的速率視為勻速[3-4]。

早高峰時期，客流量較大，當上車客流量大于列車剩余輸送能力時，站臺出現乘客滯留。第k趟列車離開站臺時的滯留乘客為：

Ra,k=max(Nall+Ra,k-1-Sa,k,0)

(1)

式中：

Ra,k——1個列車行車間隔內，第k趟列車離開站臺a時的滯留乘客數量，其中Ra,0=0，人；

Nall——1個列車行車間隔內，a站臺等待上車乘客數量，人；

Sa,k——1個列車行車間隔內，a站臺登上列車乘客數量，人。

Ra,k有兩部分來源：上一輪的滯留人數Ra,k-1，本次列車的未上車人數Nall-Sa,k。其中，Nall包含換乘上車客流和進站客流兩部分。

1.2 乘客上下車方式確定

根據乘客上下車行為不同，本文討論如下兩種極端的上下車方式:

1)方式1：乘客不遵守先下后上的原則，車上乘客的下車過程和站臺乘客的上車過程同時發生，一直處于混行狀態,此時上下車時間均等于列車的停站時間。

2)方式2：乘客嚴格遵守先下后上原則，當下車乘客下車完成之后，站臺乘客才開始上車，此時上車時間與下車時間之和為列車的停站時間。

由以上分析可知，乘客上下車過程實際上應當是這兩種方式共同發生的情況。

1.2.1 非換乘乘客側式站臺上下車混行模式

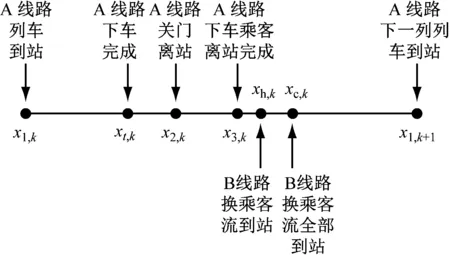
這種情況下，乘客在站臺上的聚集狀態呈現出顯著的周期性，以列車的行車間隔為周期動態變化。此時在1個周期內標記關鍵時刻，如圖1所示。

注：x1,k為第k趟列車到站時刻；x2,k為第k趟列車關門離站時刻；x3,k為第k趟列車的下車乘客疏散完畢時刻(高峰時期，設x3,k>x2,k)；x1,k+1為第k+1趟列車到站時刻。

由圖1可知，列車行車間隔ta=x1,k+1-x1,k。以前一列列車關閉車門離站時刻x2,k作為研究起始點，站臺聚集人數可以劃分為3個階段：①x2,k—x3,k階段：存在進站乘客進站和下車乘客離開站臺兩種情況；②x3,k—x1,k+1階段：只存在進站乘客進站。③x1,k+1—x2,k+1階段：存在進站乘客上車和到站乘客下車兩種情況。這3個階段中，站臺聚集人數的變化趨勢如圖2～5所示。

圖2 站臺進站客流變化曲線Fig.2 Variation pattern of inbound passenger flow on platform

1)x2,k—x3,k階段站臺聚集人數q1(x):此時站臺同時存在下車乘客疏散和上車乘客進站兩個過程。因此，該階段站臺聚集人數可以表示為：

圖3 站臺下車客流變化曲線Fig.3 Variation pattern of alighting passenger flow on platform

圖4 混行模式客流變化曲線Fig.4 Variation pattern of passenger flow in mixed mode

圖5 混行模式客流變化曲線Fig.5 Variation pattern of passenger flow in mixed mode

q1(x)=v0(x3,k-x2,k)+(vm-v0)(x-x2,k)

(2)

式中：

v0——下車乘客離開站臺的平均速率，人/s；

vm——進站乘客到達站臺的平均速率，人/s。

2)x3,k—x1,k+1階段站臺聚集人數q2(x)：在此階段，前一列列車的乘客已疏散完畢，只存在進站上車乘客。因此，該階段站臺聚集人數可以表示為：

q2(x)=vm(x-x3,k)+q(x3,k)

(3)

式中：

q(x3,k)——x3,k時刻站臺聚集人數。

將q(x3，k)代入式(3)，可得：

q2(x)=vm(x-x2,k)

(4)

3)x1,k+1—x2,k+1階段站臺聚集人數q3(x)：此階段為車門開啟時間段，在此階段同時存在乘客的上車行為和下車行為。因此，該階段的站臺聚集人數可以表示為：

通過參加職業技能大賽，貴州電子信息職業技術學院大大提升了在貴州省甚至全國的專業知名度，貴州移動、聯通、電信等公司主動與貴州電子信息職業技術學院建立校企合作關系。通過校企合作，學生的畢業論文、職前訓練、頂崗實習都在與專業相關企業進行。學校原先的畢業設計模式為教師根據所學內容劃范圍、學生選題；進行校企合作后改革為根據實際崗位群的生產案例提供選題范圍、校企雙方共同把關、學生最后確定課題的新模式。這種模式提高了學校學生的實用崗位能力[4]。

q3(x)=(vm+vc-v0-va)(x-x1,k+1)+

vm(x1,k+1-x2,k)

(5)

式中：

va——乘客上車平均速率，人/s；

vc——下車乘客平均速率，人/s。

由式(2)—式(5)可得，在1個列車行車間隔ta內，混行模式下的聚集人數變化均符合線性變化規律。為方便起見，分別用r1、r2、r3表示3個階段的站臺聚集人數變換率，即：

(6)

進站乘客一般具有隨機特性，從不同位置隨機到達車站，呈現出比較平穩的特性。下車乘客由列車運送到達，因此呈現出周期性的特點。v0一般受限于樓扶梯的通行能力，因此v0較為接近樓扶梯的最大通行能力。統計數據顯示，vm通常小于最大通行能力。一般情況下，vm0，最大聚集人數只能存在于x2,k時刻，如圖5所示。

根據上述分析可得，在非換乘乘客側式站臺上下車混行模式下，側式站臺最大聚集人數Q1(x)為：

Q1(x)=max{q(x1,k),q(x2,k)}=

(7)

在前一種模式的基礎上，添加一個下車乘客全部完成下車、上車乘客開始上車的時刻xt,k時刻，如圖6所示。

圖6 非換乘乘客側式站臺先下后上模式示意圖

同理，在先下后上模式下，任意時刻的站臺聚集人數q(x)可以表示為：

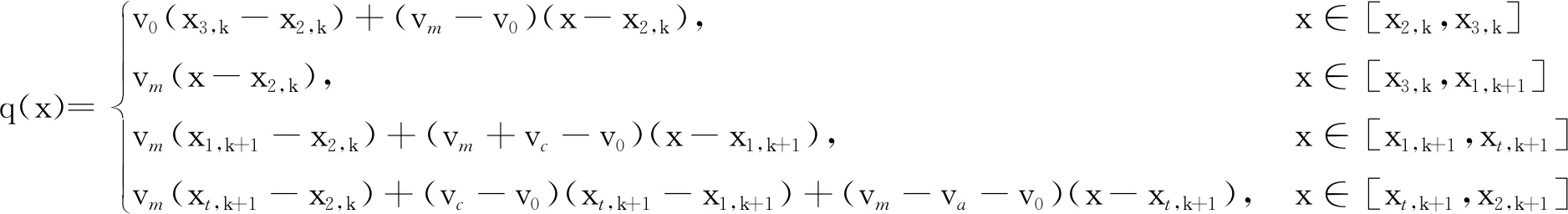
(8)

同理，在非換乘乘客側式站臺先下后上模式下，側式站臺最大聚集人數Q2(x)為：

Q2(x)=q(xt,k+1)=vm(xt,k+1-x2,k)+

(vc-v0)(xt,k+1-x1,k+1)

(9)

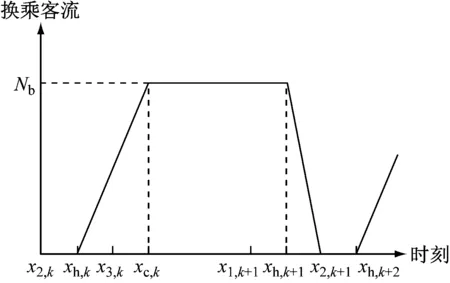
當混行模式下的r3>0時，Q1(x)=v0(x3,k-x2,k)

2 島式換乘車站站臺聚集人數模型

根據換乘客流到達車站的時刻與列車的停站時刻的不同關系，可以分為3類，如圖7所示。為獲得最大聚集人數模型，因選擇圖中③時刻作為換乘乘客到站時刻，如圖8所示。

注：xh,k為換乘客流到站時刻;xt,k為下車完成時刻。圖7 客流到達示意圖Fig.7 Schematic diagram of passenger flow arrival

注：xc,k為B線路換乘客流全部到站時刻。圖8 A線路下車結束后B線路換乘客流到達站臺

按照前述的階段劃分方式，在A線路的1個列車行車間隔ta內，同樣以前一列列車關閉車門離站時刻x2,k作為研究起始點，換乘客流站臺聚集人數可以劃分為4個階段:①x2,k—xh,k階段：此階段無換乘客流到達站臺;②xh,k—xc,k階段：換乘客流陸續到達站臺，聚集在A站臺上;③xc,k—xt,k+1階段：換乘客流聚集在A站臺上;④xt,k+1—x2,k+1階段：換乘客流和進站客流一起完成上車過程。其變化規律如圖9所示。

注：Nb為換乘總人數。圖9 站臺換乘客流變化曲線Fig.9 Variation pattern of transferring passenger flow on platform

將上車客流與下車客流按照時間同步疊加可得單側車站的換乘客流聚集人數qa(x)，可以表示為：

(10)

在列車運行過程中，滯留人數Ra,k會以列車行車間隔ta為周期，周期性出現和消失。根據式(1)可得滯留人數的判斷公式為：

Ra,k=max(Nb+vmta+Ra,k-1-va(x2,k-xt,k),0)

(11)

在1個列車行車間隔內，滯留人數的變換只存在于上車階段，其余時間段均保持不變。因此，滯留人數的變換只需要考慮[xt,k+1,x2,k+1]時間段。由于此階段持續時間較短，可將變換視作從Ra,k到Ra,k+1的勻速率變化過程。滯留人數聚集模型Ra,k(x)為：

(12)

綜上所述，側式換乘站臺聚集人數qtran(x)可以通過先下后上的側式非換乘車站聚集人數、換乘客流聚集人數、滯留人數通過時間同步疊加獲得，即：

qtran(x)=q(x)+qa(x)+Ra,k(x)

(13)

由此可得側式換乘車站聚集人數模型：

(14)

根據前述分析可得，島式換乘車站聚集人數模型q島(x)可以通過上行側式換乘車站聚集人數qtran,+(x)和下行側式換乘車站聚集人數qtran,-(x)經同步疊加獲得：

q島(x)=qtran,+(x)+qtran,-(x)

(15)

在計算最大聚集人數時，由以上分析可知，當上行和下行列車同時完成乘客下車過程時，在xt，k這一時刻的聚集人數將達到最大值。因此，島式換乘車站最大聚集人數Q3(x)為：Q3(x)=qtran,+(x)(xt,k)+qtran,-(xt,k)。

3 案例模型計算與仿真驗證

為了驗證本次研究模型的適用性、有效性，以上海軌道交通11號線(以下簡為“11號線”)江蘇路站的島式站臺作為研究對象，獲得模型所需的相關參數；利用島式換乘車站聚集人數模型，得到最高聚集人數發生時刻；使用Anylogic仿真軟件構建仿真模型，得到站臺聚集人數分布規律；比較公式計算和仿真軟件的結果，進行誤差分析。

3.1 計算參數

11號線江蘇路換乘車站為典型非同臺島式換乘車站，其客流特征、客流來源、換乘方式等滿足研究要求，可以作為驗證聚集人數模型的實例站臺。選擇換乘客流最大的工作日08:30—09:00時間段作為研究時間。根據列車運行時刻表及車站視頻數據資料可以得到如下參數：①vm=0.45人/s(根據視頻數據觀測可得，上行方向上車的客流約占65%，下行方向上車的客流約占35%，可近似認為上行方向進站客流速率為0.3人/s，下行方向進站客流速率為0.15人/s)；②va=1.8人/s；③ 換乘上車客流平均速率6人/s；④vc=1.36人/s；⑤v0=8人/s。

根據視頻數據統計得到，在早高峰期間，列車運能可以滿足乘客需求，因此11號線江蘇路站的上車客流不存在未上車的滯留乘客，即：Ra,k=0。

3.2 模型計算結果分析

按照島式換乘站臺聚集人數模型，可得島式換乘車站聚集人數模型，如圖10所示。

圖10 模型計算的11號線江蘇路站站臺聚集人數分布圖

由圖10可見，站臺最大聚集人數出現在上下行列車同時完成下車過程的80 s時，達到了1 252人，即上行側最大聚集人數644人和下行側最大聚集人數608人。同時可以看到，在230 s時的聚集人數相鄰峰值的數值差異主要是由上下車到達時刻不同所致，200 s時的聚集人數峰值是由上行側列車到站客流產生的。

3.3 仿真驗證

采用Anylogic仿真軟件搭建模型，按比例建立的11號線江蘇路站站臺模型如圖11所示，站臺相應的設施按照比例尺等比例放置。通過行人庫建立邏輯關系，即包括進站客流、換乘客流和出站客流的控制模塊。

圖11 11號線江蘇路站站臺仿真模型圖Fig.11 Simulation diagram of platform simulation model of Shanghai Rail Transit Line 11 Jiangsu Road Station

聚集人數的采樣時間頻率設置為1 s，每隔1 s采集1個聚集人數樣本，共采集600個數據，通過Anylogic仿真軟件的數據輸出功能統計最大聚集人數，如圖12示。圖12采用模型運行穩定后20～30 min時間段的數據。

由仿真結果可知：本次仿真站臺的最高聚集人數為1 237人，出現在26 min時，即上下行列車同時到達站臺的時刻；站臺的聚集人數根據時間變化而變化，每當上下行列車同時到達站臺并且換乘乘客全部到達站臺時，可以達到最高聚集人數1 237人，相對誤差-1.24%；聚集人數呈現出以10 min為周期的變化規律。

圖12 仿真計算的11號線江蘇路站站臺聚集人數分布圖

為了驗證本文提出模型的有效性，得到10組站臺最大聚集人數仿真計算結果與模型計算結果的相對誤差，如表1所示。由表1可見，站臺平均聚集人數為1 258人，平均相對誤差為0.47%；10組仿真結果的相對誤差均在3%之內。由此可見，模型計算的站臺最高聚集人數可以有效反映仿真計算的站臺最高聚集人數。

表1 站臺最大聚集人數仿真計算與模型計算的相對誤差

4 結語

以列車行車間隔為研究周期，分析乘客在站臺的集散過程，建立了換乘車站站臺最大聚集人數計算模型。將站臺客流分為進站客流、換乘客流和出站客流，獲得了基于列車時刻表的換乘站臺聚集人數模型，并且通過Anylogic仿真軟件驗證了站臺聚集人數模型的有效性和適用性，可為城市軌道交通換乘車站站臺客流壓力評估提供理論支撐。

本次研究所建立的站臺聚集人數模型中，客流的到達采用的都是勻速到達模式。而在實際中，會存在個體的差異性，將該差異對模型精準度的影響作為下一步的研究方向。