軌道交通列車永磁同步電機(jī)渦流損耗抑制措施研究*
于海闊 張利軍 靳 凱 畢京斌 趙海波
(1. 中車青島四方車輛研究所有限公司, 266031, 青島;2. 中車長(zhǎng)春軌道客車股份有限公司, 130062, 長(zhǎng)春∥第一作者, 工程師)
0 引言
軌道交通列車應(yīng)用的PMSM (永磁同步電機(jī))以其損耗小、效率高、體積小、質(zhì)量輕、結(jié)構(gòu)多樣化、可靠性高、過載能力強(qiáng)等優(yōu)點(diǎn)成為輪轂電機(jī)的首選。但是,在PMSM中,永磁體和帶槽電樞鐵心相互作用,產(chǎn)生齒槽轉(zhuǎn)矩,進(jìn)而產(chǎn)生振動(dòng)和噪聲,影響系統(tǒng)的控制精度。除此之外,受輪轂電機(jī)體積限制,永磁體產(chǎn)生的渦流損耗會(huì)使其自身產(chǎn)生高溫,面臨不可逆退磁的風(fēng)險(xiǎn)。
從PMSM齒槽轉(zhuǎn)矩產(chǎn)生的機(jī)理出發(fā),削弱齒槽轉(zhuǎn)矩大致可從極和槽兩方面考慮。文獻(xiàn)[1]從磁極優(yōu)化角度出發(fā),把減小氣隙磁密諧波分量作為削弱齒槽轉(zhuǎn)矩的依據(jù),分析了不同轉(zhuǎn)子磁極優(yōu)化技術(shù)的優(yōu)、缺點(diǎn)。文獻(xiàn)[2]采用優(yōu)化磁極形狀的方法,提出了兩種凸形不等厚磁極的永磁電機(jī),相比于傳統(tǒng)表貼瓦片形永磁電機(jī)降低了rTHD(氣隙磁密諧波畸變率)和齒槽轉(zhuǎn)矩,增大了電磁轉(zhuǎn)矩,但未分析對(duì)電機(jī)轉(zhuǎn)矩脈動(dòng)的影響。文獻(xiàn)[3]采用偏心磁極來優(yōu)化表貼式PMSM氣隙磁密波形,推導(dǎo)了偏心磁極電機(jī)氣隙磁密解析表達(dá)式;結(jié)合樣機(jī)試驗(yàn)證明了計(jì)算方法的準(zhǔn)確性,但是生產(chǎn)制造復(fù)雜、成本高。不同于磁極優(yōu)化技術(shù),研究電機(jī)解析模型中定子開槽對(duì)氣隙磁場(chǎng)的影響,可進(jìn)一步分析齒槽轉(zhuǎn)矩。文獻(xiàn)[4]在文獻(xiàn)[5-6]的基礎(chǔ)上,采用保角變換法推導(dǎo)出二維極坐標(biāo)系下的相對(duì)磁導(dǎo)函數(shù),進(jìn)而得到表貼式PMSM定子開槽狀況下的氣隙磁場(chǎng)分布,但所得到的氣隙磁場(chǎng)分布并不完整。文獻(xiàn)[11]采用保角變換法推導(dǎo)出復(fù)相對(duì)磁導(dǎo)函數(shù),得到完整的氣隙磁場(chǎng)分布,但求解過程復(fù)雜、計(jì)算時(shí)間長(zhǎng);定子槽為無限深單槽模型,無法考慮槽與槽間的影響,不利于反電勢(shì)的精確計(jì)算。文獻(xiàn)[12]采用數(shù)值、解析相結(jié)合的方法推導(dǎo)了定子開槽下PMSM氣隙磁場(chǎng)分布,但計(jì)算耗時(shí)長(zhǎng),且受迭代精度影響。不同于上述文獻(xiàn)中提到的開槽PMSM氣隙磁場(chǎng)解析方法,精確子域模型法能夠考慮到定子槽間相互影響,且會(huì)根據(jù)材料屬性和電機(jī)結(jié)構(gòu)將電機(jī)劃分為不同的子域,在計(jì)算電磁性能方面具有較高的精度。文獻(xiàn)[13]在PMSM解析建模中考慮了導(dǎo)磁材料磁導(dǎo)率為具體數(shù)值的情況,結(jié)合精確子域模型法推導(dǎo)了電機(jī)氣隙磁密,以及空載工況下的反電動(dòng)勢(shì)及輸出轉(zhuǎn)矩的表達(dá)式,探究了極弧系數(shù)和槽開口寬度對(duì)輸出轉(zhuǎn)矩的影響,但未分析對(duì)氣隙磁密和齒槽轉(zhuǎn)矩的影響,且所建模型中槽型尺寸僅由槽口寬度決定,實(shí)用性較差。
針對(duì)永磁體渦流損耗的抑制,最常用的方法是磁極分段。文獻(xiàn)[14]研究了Halbach充磁方式下永磁體每極分塊數(shù)對(duì)齒槽轉(zhuǎn)矩的影響,證明每極分塊數(shù)目越多越能改善磁場(chǎng)分布,但會(huì)增加制造成本。文獻(xiàn)[15]提出了一種環(huán)形部分分段結(jié)構(gòu),比較了永磁體單側(cè)、雙側(cè)部分分段,以及單側(cè)、雙側(cè)環(huán)形部分分段的渦流損耗。永磁體部分分段在保持一定機(jī)械強(qiáng)度的基礎(chǔ)上,可以保證永磁體的完整性,不需要額外的工藝及成本。
針對(duì)以上問題,以rTHD、齒槽轉(zhuǎn)矩及渦流損耗最小為優(yōu)化目標(biāo),提出一種十字型部分分段Halbach PMSM解析模型,推導(dǎo)出十字型部分分段并考慮定子開槽效應(yīng)下的氣隙磁密解析表達(dá)式,計(jì)算得到PMSM的齒槽轉(zhuǎn)矩和電磁轉(zhuǎn)矩,通過有限元仿真驗(yàn)證了解析結(jié)果的準(zhǔn)確性,并且系統(tǒng)地分析了極間間隔角度、邊界磁極的充磁角度、主磁極高度和寬度、剖去部分深度和寬度對(duì)徑向氣隙磁密的基波幅值和rTHD的影響。
1 PMSM解析模型的構(gòu)建
1.1 PMSM解析模型
建立二維極坐標(biāo)系,采用精確子域模型法分析定子開槽下的氣隙磁場(chǎng)分布。為便于分析計(jì)算,做出如下假設(shè):① 永磁體材料具有線性退磁特性;② 忽略端部影響;③ 鐵磁材料磁導(dǎo)率無窮大。
圖1為十字型部分分段Halbach PMSM在空載工況下的氣隙磁場(chǎng)和電樞反應(yīng)磁場(chǎng)解析模型。
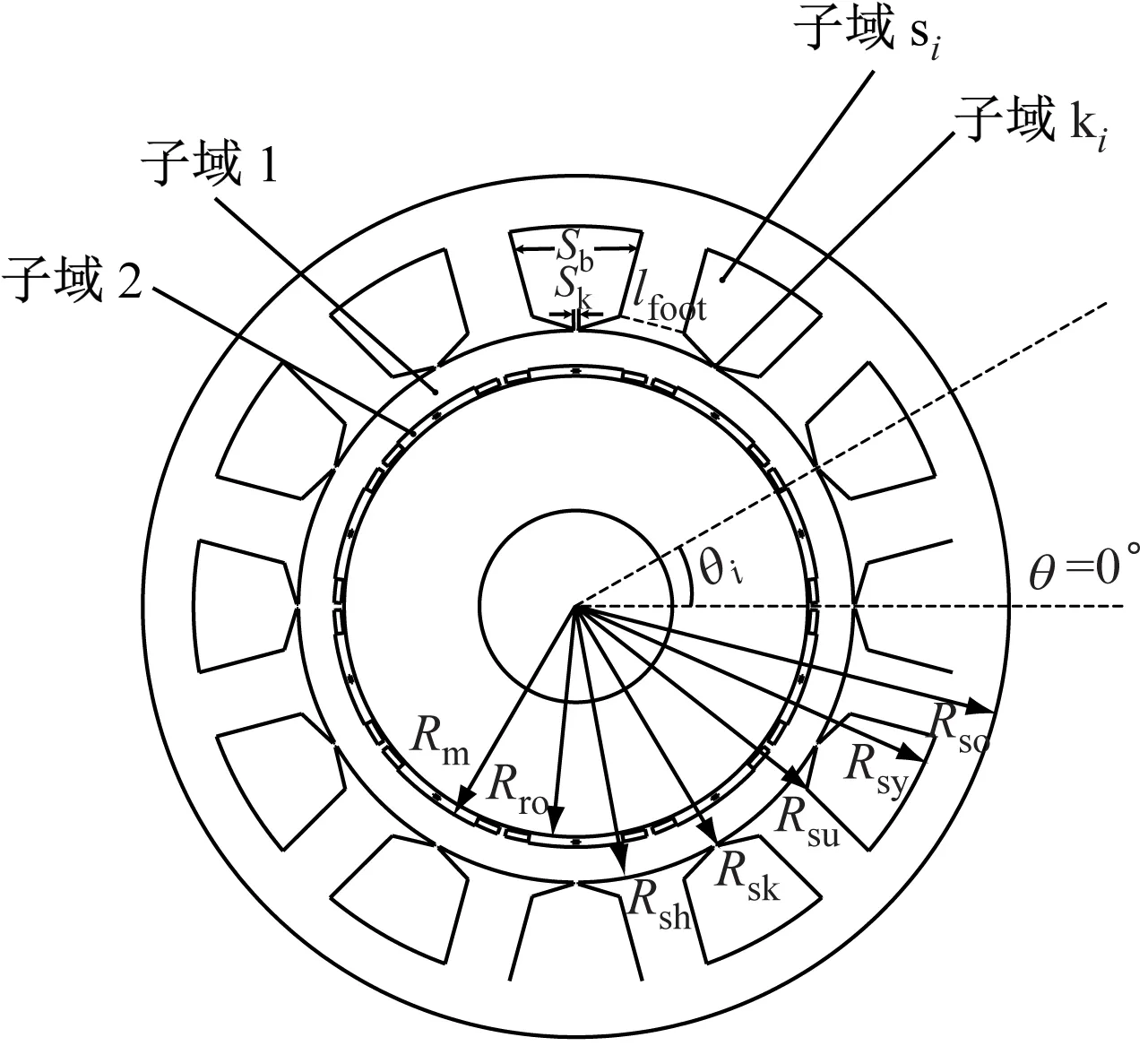
a) 空載工況下的氣隙磁場(chǎng)解析模型
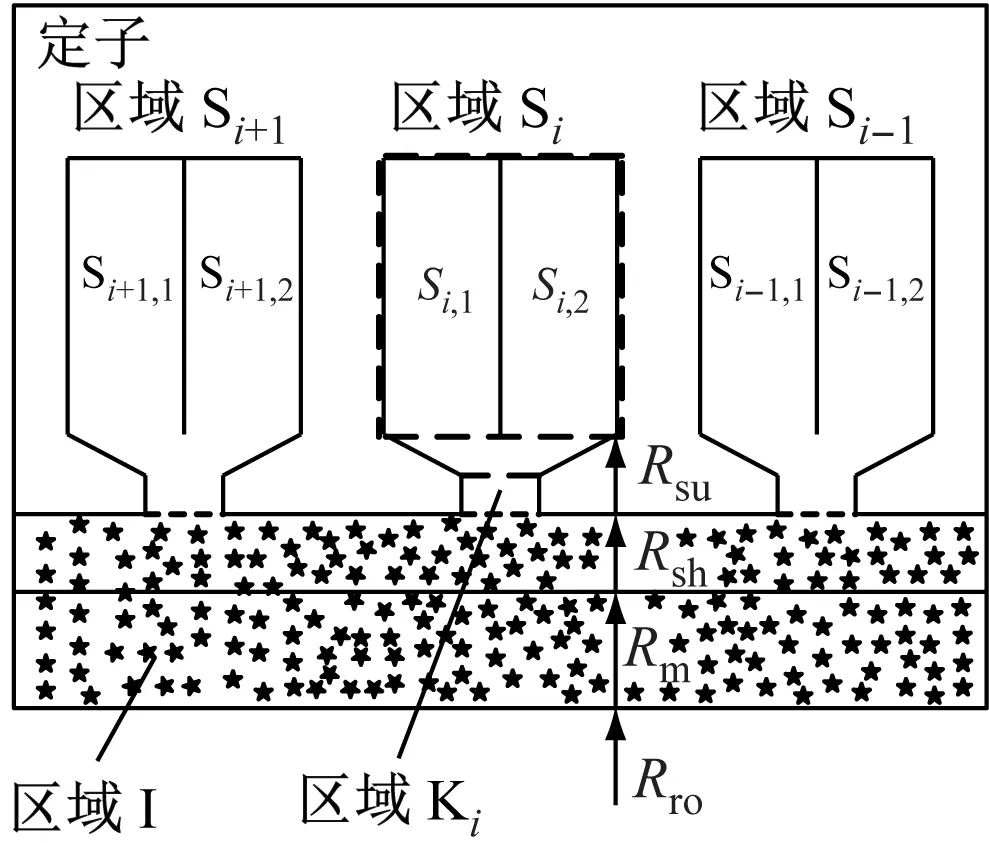
b) 電樞反應(yīng)磁場(chǎng)解析模型
將圖1 a) 所示的空載工況下PKPM的氣隙磁場(chǎng)解析模型在二維極坐標(biāo)系下劃分為4個(gè)區(qū)域:氣隙區(qū)域(1),永磁體區(qū)域(2),第i個(gè)槽口區(qū)域(ki)、第i個(gè)槽身區(qū)域(si)。
將圖1 b)所示的電樞反應(yīng)磁場(chǎng)解析模型在二維極坐標(biāo)系下劃分為3個(gè)區(qū)域:等效氣隙區(qū)域(Ι),第i個(gè)槽口區(qū)域(Ki)、第i個(gè)槽身區(qū)域(Si)。
1.2 十字型部分分段Halbach PMSM解析模型
永磁體采用平行充磁。圖2為待優(yōu)化的十字型部分分段磁極結(jié)構(gòu)。在1對(duì)磁極下,永磁體磁化強(qiáng)度M可以表示為:
M=Br/μ0
(1)
式中:
Br——永磁體剩磁;
μ0——真空磁導(dǎo)率。

注:lm為主磁極厚度; ls為邊界磁極厚度; hm為中心剖去部分厚度。
2 空載工況下PMSM解析模型氣隙磁場(chǎng)計(jì)算分析
2.1 矢量磁位方程的建立及其求解
空載氣隙磁場(chǎng)計(jì)算的一般方程為:
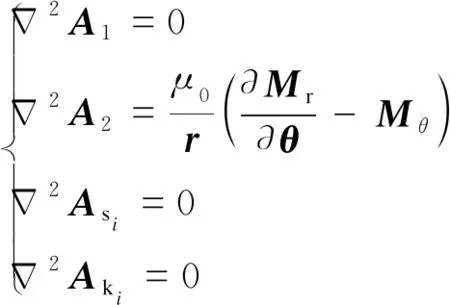
(2)
式中:
Mr——徑向磁化強(qiáng)度矢量分量;
Mθ——切向磁化強(qiáng)度矢量分量;
A1、A2、Asi、Aki——分別為氣隙區(qū)域、Halbach型永磁體區(qū)域、第i個(gè)槽身區(qū)域si和第i個(gè)槽口區(qū)域ki內(nèi)的矢量磁位;
r、θ——分別為極坐標(biāo)系下的徑向和切向分量。
由分離變量法,得到各區(qū)域矢量磁位通解表達(dá)式:
(3)
其中:
(4)
式中:
n、m、j——相應(yīng)區(qū)域內(nèi)矢量磁位的諧波次數(shù);
θ0——轉(zhuǎn)子初始位置角;
g——2p和Q的最大公約數(shù);
A1n、B1n、C1n、D1n、A2n、B2n、C2n、D2n、Asi,j、Asi,m、Aki,0、Aki,j、Bki,j——分別為空載工況下氣隙磁場(chǎng)的待定系數(shù);
Mr,n(n)、Mθ,n(n)——分別為Mn(n)的徑向和切向磁化強(qiáng)度矢量分量。
各子域邊界需滿足如下條件:
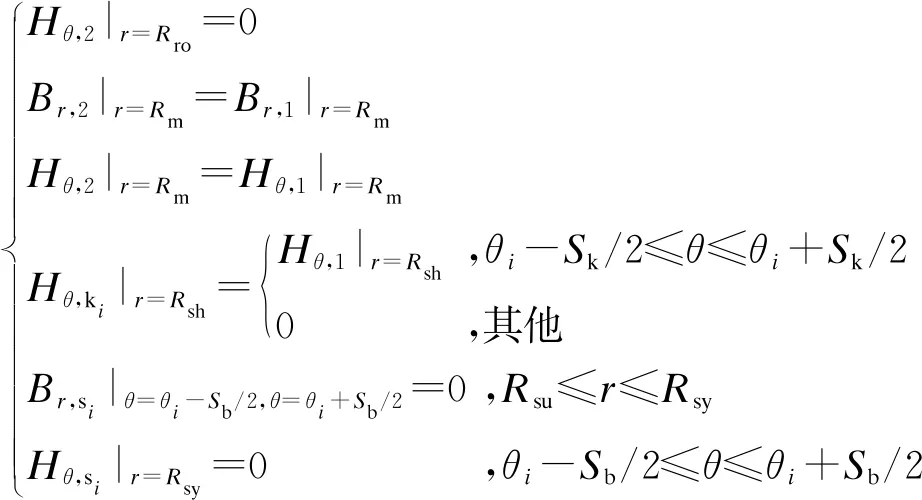
(5)
式中:
Hθ,1、Hθ,2、Hθ,si、Hθ,ki——分別為子域1、2、si、ki的切向磁場(chǎng)強(qiáng)度;
Br,1、Br,2、Br,si——分別為子域1、2、si的徑向氣隙磁密。
2.2 空載工況下PMSM的氣隙磁密

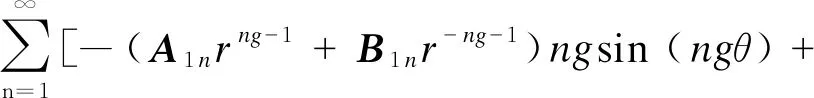
(C1nrng-1+D1nr-ng-1)ngcos (ngθ)]
(6)
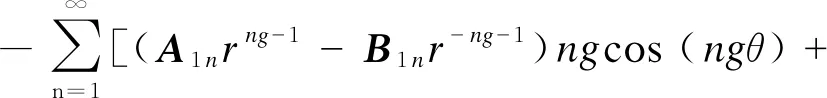
(C1nrng-1-D1nr-ng-1)ngsin (ngθ)]
(7)
Bθ,1——空載氣隙子域1的切向氣隙磁密。
2.3 齒槽轉(zhuǎn)矩的計(jì)算
由空載工況下的氣隙磁密分布計(jì)算結(jié)果,利用麥克斯韋應(yīng)力張量法,得到齒槽轉(zhuǎn)矩Tcog的表達(dá)式:
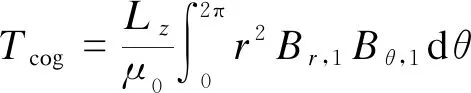
(8)
式中:
Lz——電機(jī)軸向長(zhǎng)度。
3 PMSM電樞反應(yīng)磁場(chǎng)解析模型分析
3.1 矢量磁位方程的建立與求解
電樞反應(yīng)磁場(chǎng)計(jì)算時(shí),永磁體不充磁。施加電流源激勵(lì)后,永磁體磁場(chǎng)計(jì)算的一般方程為:
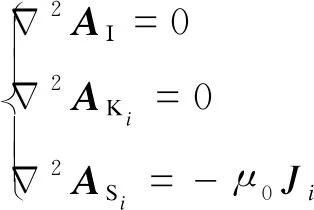
(9)
式中:
AΙ、AKi、ASi——各區(qū)域內(nèi)的矢量磁位;
Ji——第i個(gè)槽內(nèi)繞組的電流密度。
根據(jù)前面的分析,筆者認(rèn)為中國(guó)目前政治、社會(huì)制度的條件,比如傳統(tǒng)的集權(quán)影響、幅員遼闊差異巨大、社會(huì)自治基礎(chǔ)和能力不足等,不具備央地徹底分權(quán)模式的條件,可行的模式是應(yīng)該探索中央統(tǒng)一領(lǐng)導(dǎo)、地方授權(quán)執(zhí)行的分權(quán)模式,在其中不斷探索合理授權(quán)地方的機(jī)制,從而實(shí)現(xiàn)央地之間權(quán)責(zé)內(nèi)洽的機(jī)制建立。
由分離變量法,得到各區(qū)域矢量磁位通解的表達(dá)式:
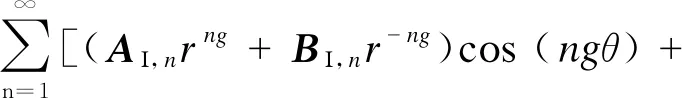
(CΙ,nrng+DΙ,nr-ng)sin (ngθ)]
(10)
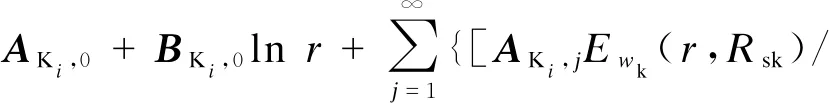
Ewk(Rsh,Rsk)-BKi,jEwk(r,Rsh)/
Ewk(Rsh,Rsk)]cos[wk(θ-θi+Sk/2)]}
(11)
ASi=ASi,0+ACi(r)+
(12)
式中:
AΙ,n、BΙ,n、CΙ,n、DΙ,n——子域Ι電樞反應(yīng)氣隙磁場(chǎng)的待定系數(shù);
AKi,0、BKi,0、AKi,j、BKi,j——子域Ki電樞反應(yīng)氣隙磁場(chǎng)的待定系數(shù);
ASi,0、ACi、ASi,m——子域Si電樞反應(yīng)氣隙磁場(chǎng)的待定系數(shù)。
各區(qū)域的邊界條件如下:

(13)
式中:
Hθ,Ι、Hθ,Ki——分別為子域Ι、Ki的切向磁場(chǎng)強(qiáng)度;
ASi,1、ASi,2——分別為槽身子域Si處繞組1和繞組2產(chǎn)生的磁位。
3.2 等效氣隙磁密的計(jì)算
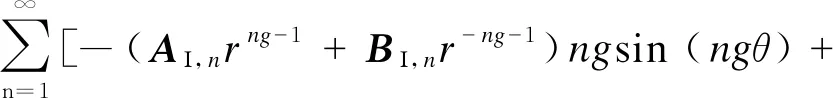
(CΙ,nrng-1+DΙ,nr-ng-1)ngcos (ngθ)]
(14)

(CΙ,nrng-1-DΙ,nr-ng-1)ngsin (ngθ)]
(15)
式中:
Br,Ι——電樞反應(yīng)磁場(chǎng)等效氣隙子域Ι的徑向氣隙磁密;
Bθ,Ι——電樞反應(yīng)磁場(chǎng)等效氣隙子域Ι的切向氣隙磁密。
4 負(fù)載工況下PMSM的磁場(chǎng)分析
4.1 氣隙磁密的計(jì)算
由疊加定理可得:

(16)
式中:
Br,t、Bθ,t——分別為負(fù)載氣隙子域徑向和切向氣隙磁密。
4.2 電磁轉(zhuǎn)矩的計(jì)算
由負(fù)載氣隙磁密分布結(jié)果,利用麥克斯韋應(yīng)力張量法,得到電磁轉(zhuǎn)矩Tem的表達(dá)式:
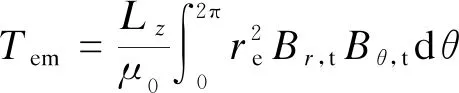
(17)
式中:
re——電磁轉(zhuǎn)矩積分半徑。
5 十字型主磁極中心部分分段Halbach PMSM解析模型有限元分析驗(yàn)證
為驗(yàn)證上述解析模型的正確性,對(duì)如圖3所示的十字型部分分段Halbach PMSM模型進(jìn)行有限元仿真分析。該電機(jī)模型是在Halbach陣列基礎(chǔ)上添加了極間隔斷,并將每極分為不等寬、不等厚的3塊。為降低渦流損耗,得到更加正弦的氣隙磁密波形和較低的齒槽轉(zhuǎn)矩,對(duì)主磁極中心部分進(jìn)行分段,使邊界磁極幾何中心與主磁極幾何中心在同一條圓弧上。電機(jī)模型的主要參數(shù)如表1所示。根據(jù)解析計(jì)算結(jié)果對(duì)永磁體的極間間隔角度、邊界磁極的充磁角度、主磁極高度和寬度、剖去部分深度和寬度進(jìn)行多變量分級(jí)優(yōu)化設(shè)計(jì),并與普通表貼結(jié)構(gòu)、普通表貼部分分段結(jié)構(gòu)、等厚等寬Halbach結(jié)構(gòu)、T型Halbach結(jié)構(gòu)、Hat型Halbach結(jié)構(gòu)、T型部分分段Halbach結(jié)構(gòu)及Hat型部分分段Halbach結(jié)構(gòu)的電磁性能進(jìn)行對(duì)比,驗(yàn)證十字型部分分段Halbach PMSM結(jié)構(gòu)的有效性及優(yōu)越性。

圖3 十字型部分分段Halbach PMSM模型示意圖

表1 十字型部分分段Halbach PMSM的主要參數(shù)
5.1 空載工況下PMSM的仿真波形
圖4~5為空載工況下的十字型部分分段Halbach PMSM解析模型和FEA(有限元分析)模型的氣隙磁密和齒槽轉(zhuǎn)矩[17]。
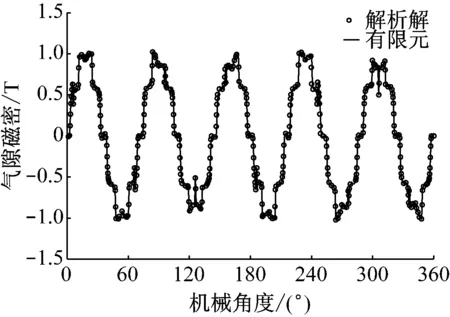
圖4 不同模型下氣隙磁密隨機(jī)械角度變化對(duì)比曲線
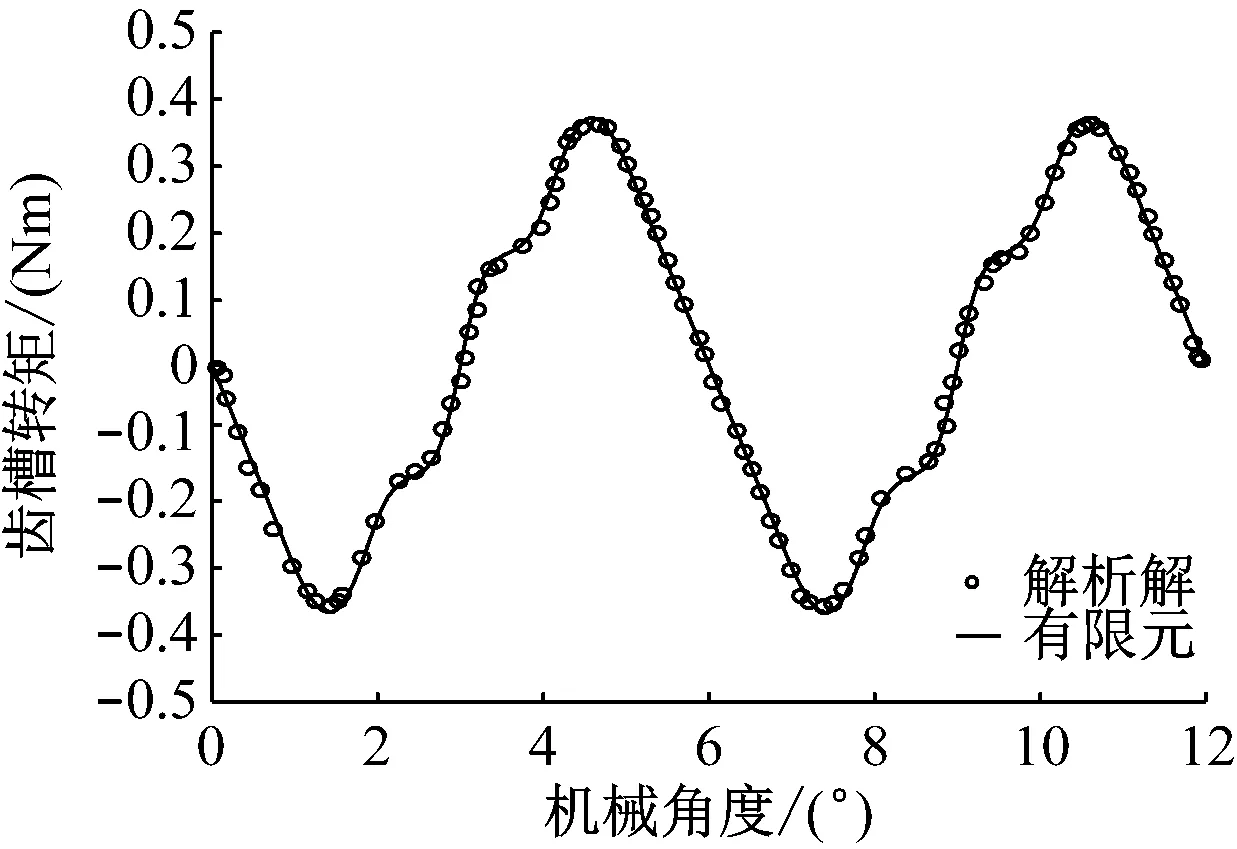
圖5 不同模型下齒槽轉(zhuǎn)矩隨機(jī)械角度變化對(duì)比曲線
由圖4~5可見,PMSM模型的氣隙磁密和齒槽轉(zhuǎn)矩的解析解和FEA解基本吻合,驗(yàn)證了PMSM解析模型的正確性,為永磁體結(jié)構(gòu)的進(jìn)一步優(yōu)化奠定基礎(chǔ)。
對(duì)永磁體的極間間隔角度進(jìn)行優(yōu)化,以rTHD為確定指標(biāo)得到極間間隔角度為6°。改變FEA模型中邊界磁極的充磁角度b,令b在0°~90°內(nèi),每隔10°取1個(gè)值,得到空載工況下PMSM模型的氣隙磁密基波幅值和rTHD隨b的變化曲線,如圖6所示。由圖6可見,隨著b增大,rTHD先略微減小再增大,基波幅值則一直減小;當(dāng)b=0°時(shí),基波幅值的最大值為1.035 T;當(dāng)b=10°時(shí),rTHD的最小值為20.8%,基波幅值為1.032 T。因此,選取10°作為邊界磁極的充磁角度。
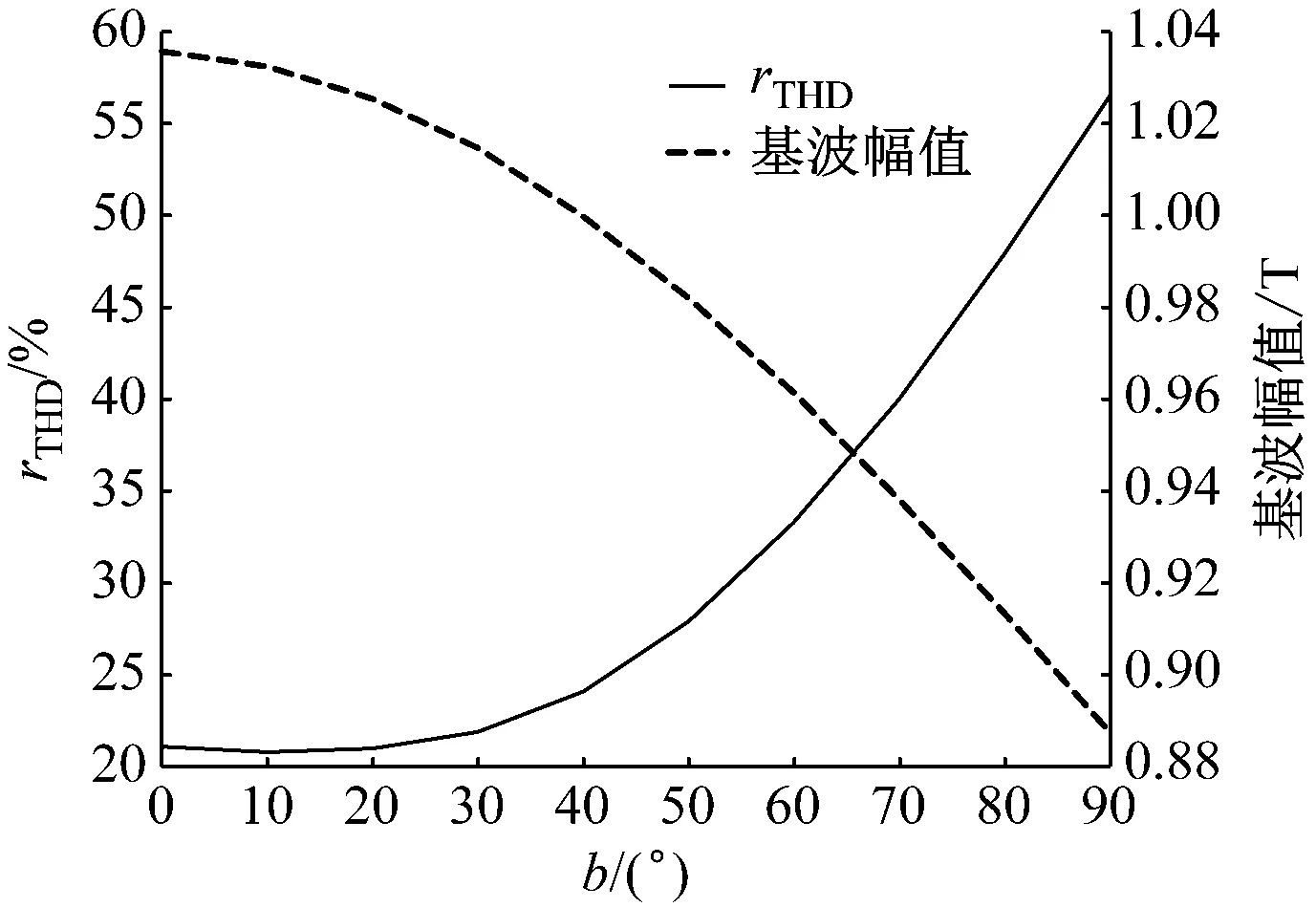
圖6 諧波畸變率和基波幅值隨b的變化曲線
當(dāng)極間間隔角度為定值時(shí),主磁極與邊界磁極所占角度之和亦為定值。通過改變主磁極角度θm及邊界磁極厚度ls,使θm在0°~20°內(nèi)(每隔2°取1個(gè)值),使ls在1~3 mm內(nèi)(每隔0.25 mm取1個(gè)值),得到空載工況下PMSM的氣隙磁密rTHD的變化曲線,如圖7所示。

圖7 PMSM的rTHD隨θm的變化曲線Fig.7 Curve of PMSM rTHDchanging with θm
由圖7可見,當(dāng)θm為定值時(shí),隨著ls增大,rTHD先減小后增大,且ls的轉(zhuǎn)折點(diǎn)在1.75~2.00 mm范圍內(nèi)。綜合圖7仿真結(jié)果,令θm在12°~16°內(nèi),每隔1°取1個(gè)值; 令ls在1.5~1.9 mm內(nèi),每隔0.1 mm取1個(gè)值,通過進(jìn)一步優(yōu)化,得到圖8所示曲線。
由圖8可見,當(dāng)ls為定值時(shí),隨著θm的增大rTHD先減小后增大,θm的轉(zhuǎn)折點(diǎn)為13°。為進(jìn)一步縮小最優(yōu)參數(shù)范圍,令θm分別為12°、13°、14°時(shí),ls分別為1.7 mm、1.8 mm、1.9 mm。
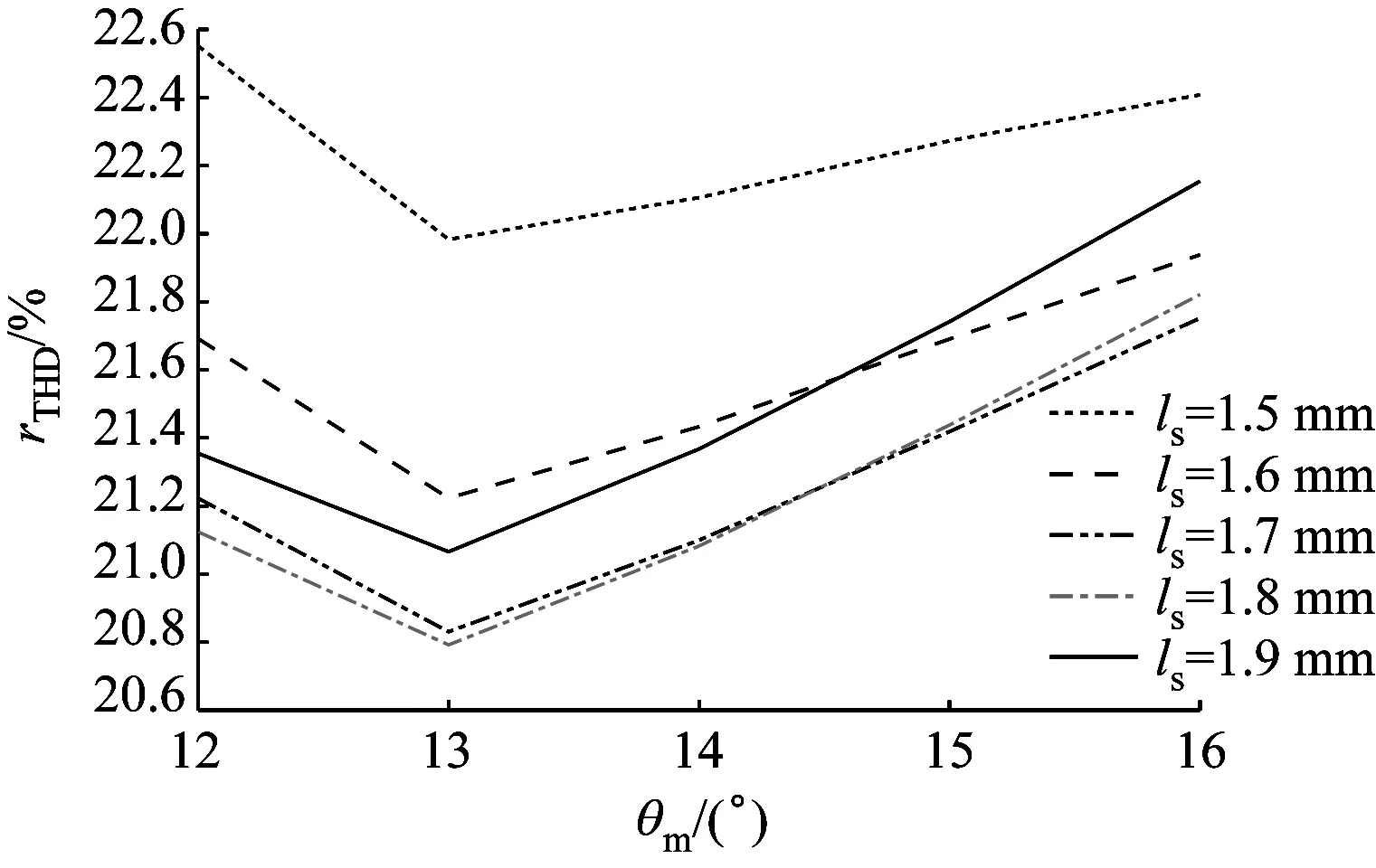
圖8 PMSM的rTHD隨θm的變化曲線Fig.8 Curve of PMSM rTHDchanging with θm
改變PMSM有限元模型中主磁極中心部分分段深度hm和角度θcm。令hm在0~3 mm內(nèi),每隔0.5 mm取1個(gè)值;令θcm在0°~30°內(nèi),每隔3°取1個(gè)值。得到空載工況下rTHD隨θm的變化曲線,如圖9所示。
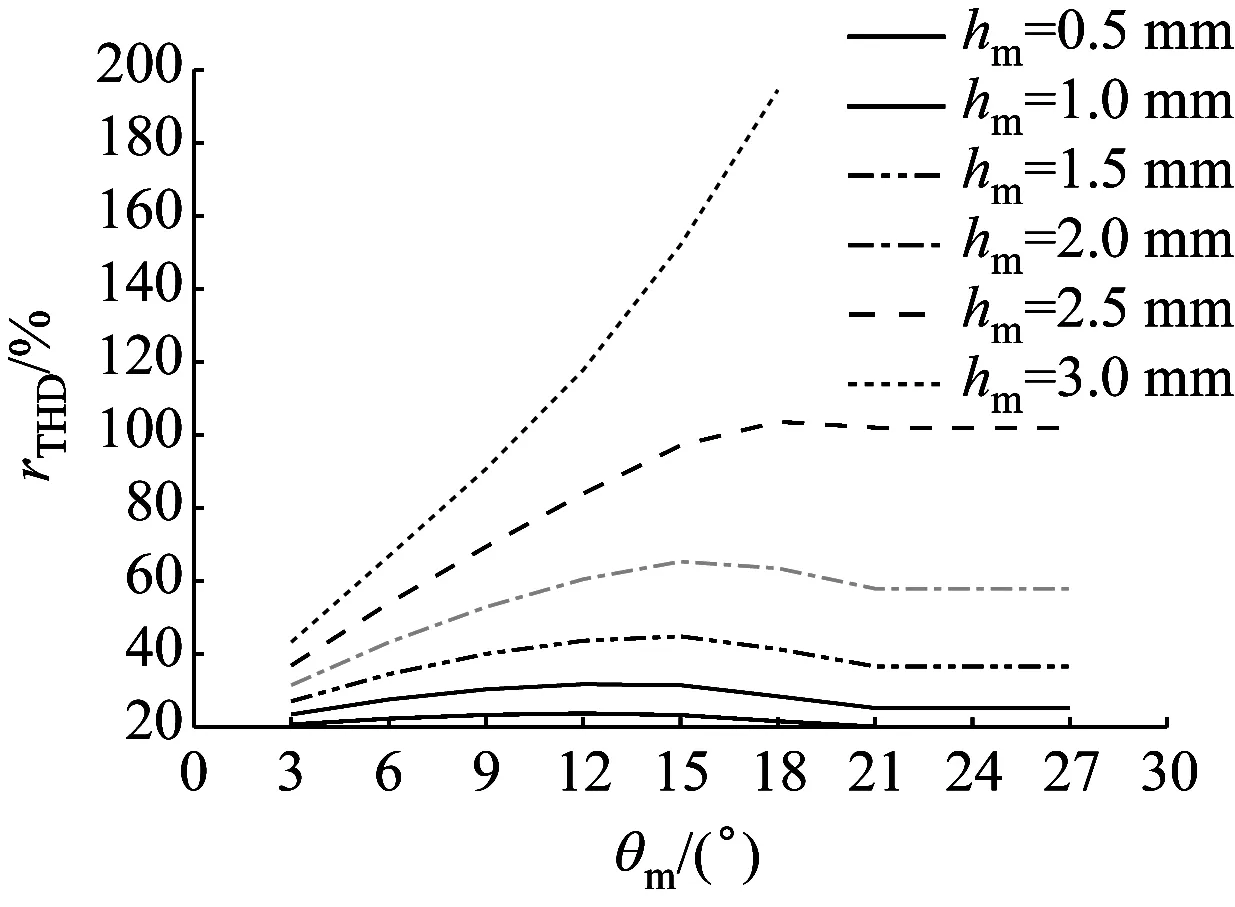
圖9 PMSM的rTHD隨θcm的變化曲線Fig.9 Curve of PMSM rTHD changing with θcm
從圖9中可以看出,當(dāng)θcm為定值時(shí),rTHD隨hm的增大而增大;當(dāng)hm為定值時(shí),rTHD隨θcm的增大先增大后減小。考慮到永磁體的完整性及機(jī)械強(qiáng)度,hm不能超過永磁體厚度的65%,即hm≤1.95 mm。綜合圖9仿真結(jié)果,令θcm在3°~7°內(nèi),每隔1°取1個(gè)值;令hm在0.1~0.5 mm內(nèi),每隔0.1 mm取1個(gè)值,通過進(jìn)一步優(yōu)化,得到圖10所示曲線。
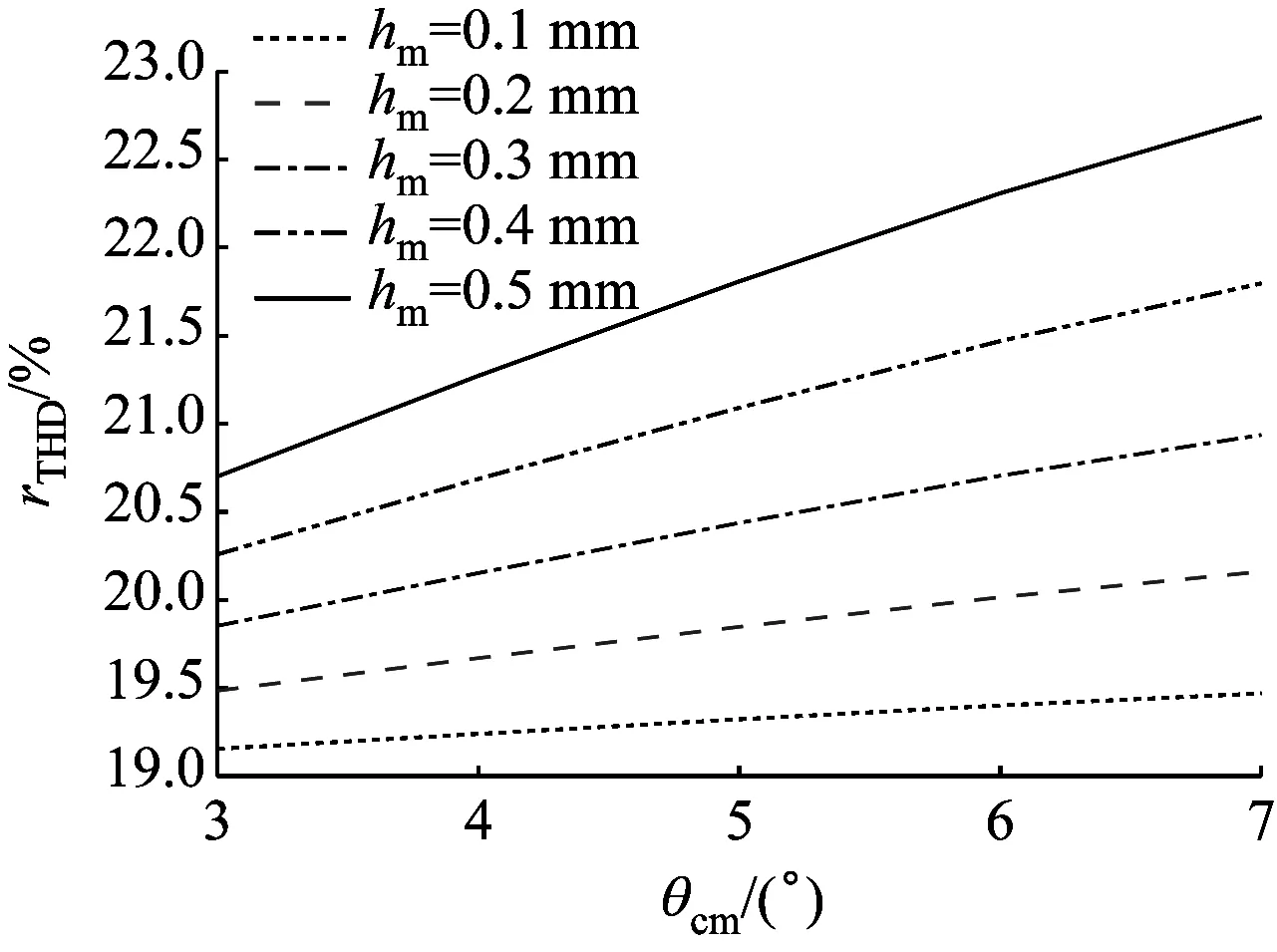
圖10 PMSM的rTHD隨θcm的變化曲線Fig.10 Curve of PMSM rTHD changing with θcm
綜合圖10仿真結(jié)果,考慮到PMSM實(shí)際制作工藝和成本,令θcm分別為3°、4°、5°,hm分別為0.2 mm、0.3 mm、0.4 mm。將θcm、hm與θm、ls進(jìn)行多變量?jī)?yōu)化,得到圖11所示仿真結(jié)果,以尋出最優(yōu)參數(shù)組合。
圖11為主磁極剖去角度θcm分別為3°、4°、5°時(shí),rTHD隨θm、ls和hm的變化曲線。當(dāng)θm=13°、ls=1.9 mm、θcm=3°及hm=0.2 mm時(shí)rTHD有最優(yōu)解。至此,在空載工況下完成了對(duì)十字型部分分段Halbach結(jié)構(gòu)的優(yōu)化。將優(yōu)化后rTHD的最優(yōu)解應(yīng)用于其他8種電機(jī)結(jié)構(gòu),得到圖12所示的齒槽轉(zhuǎn)矩變化曲線和圖13所示的渦流損耗變化曲線。

a) θcm = 3°

b) θcm = 4°
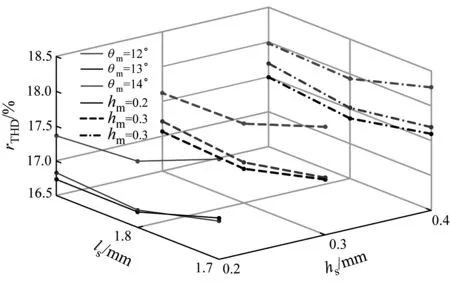
c) θcm = 5°圖11 PMSM多變量?jī)?yōu)化后rTHD變化曲線
由圖12可見,普通表貼式PMSM齒槽轉(zhuǎn)矩為820.27 mNm,普通表貼部分分段PMSM齒槽轉(zhuǎn)矩為832.71 mNm;等寬等厚Halbach PMSM齒槽轉(zhuǎn)矩為585.08 mNm,Hat型Halbach PMSM齒槽轉(zhuǎn)矩為472.02 mNm,Hat型部分分段Halbach PMSM齒槽轉(zhuǎn)矩為459.12 mNm;T型Halbach PMSM齒槽轉(zhuǎn)矩為493.46 mNm,T型部分分段Halbach PMSM齒槽轉(zhuǎn)矩為481.32 mNm;十字型Halbach PMSM齒槽轉(zhuǎn)矩為413.56 mNm,十字型部分分段Halbach PMSM齒槽轉(zhuǎn)矩為385.84 mNm。
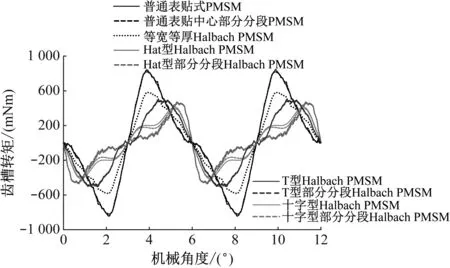
圖12 優(yōu)化后9種電機(jī)結(jié)構(gòu)齒槽轉(zhuǎn)矩隨機(jī)械角度的變化曲線

圖13 優(yōu)化后9種結(jié)構(gòu)渦流損耗隨時(shí)間的變化曲線
由圖13可見,普通表貼式PMSM渦流損耗為61.72 W,普通表貼中心部分分段PMSM渦流損耗為60.29 W;等寬等厚Halbach PMSM渦流損耗為18.68 W, Hat型Halbach PMSM渦流損耗為14.80 W,Hat型部分分段Halbach PMSM渦流損耗為14.23 W;T型Halbach PMSM渦流損耗為14.72 W,T型部分分段Halbach PMSM渦流損耗為14.15 W;十字型Halbach PMSM渦流損耗為14.57 W,十字型部分分段Halbach PMSM渦流損耗為14.03 W。綜合上述數(shù)據(jù),相比于普通表貼式PMSM,等寬等厚Halbach充磁方式下的PMSM渦流損耗降低了69.73%;相比于Hat型和T型的Halbach PMSM,十字型Halbach PMSM渦流損耗更小;相比于主磁極不分段的PMSM,主磁極中心部分分段結(jié)構(gòu)的PMSM降低了渦流損耗。
5.2 永磁體負(fù)載反應(yīng)磁場(chǎng)仿真波形
空載工況下PMSM的反應(yīng)磁場(chǎng)和電樞反應(yīng)磁場(chǎng)的疊加即為負(fù)載反應(yīng)磁場(chǎng),此時(shí)永磁體和激勵(lì)電流源同時(shí)作用。由PMSM的主要參數(shù)(見表1)推算出所施加電流源激勵(lì)的A相電流有效值Im為30 A,A相電流初相位為30°。選取r=(Rsh+Rm)/2作為氣隙線半徑,提取負(fù)載氣隙磁密,得到如圖14所示波形。由圖14可見,負(fù)載氣隙磁密的解析解與有限元解吻合。電磁轉(zhuǎn)矩的解析解與有限元解對(duì)比如圖15所示。
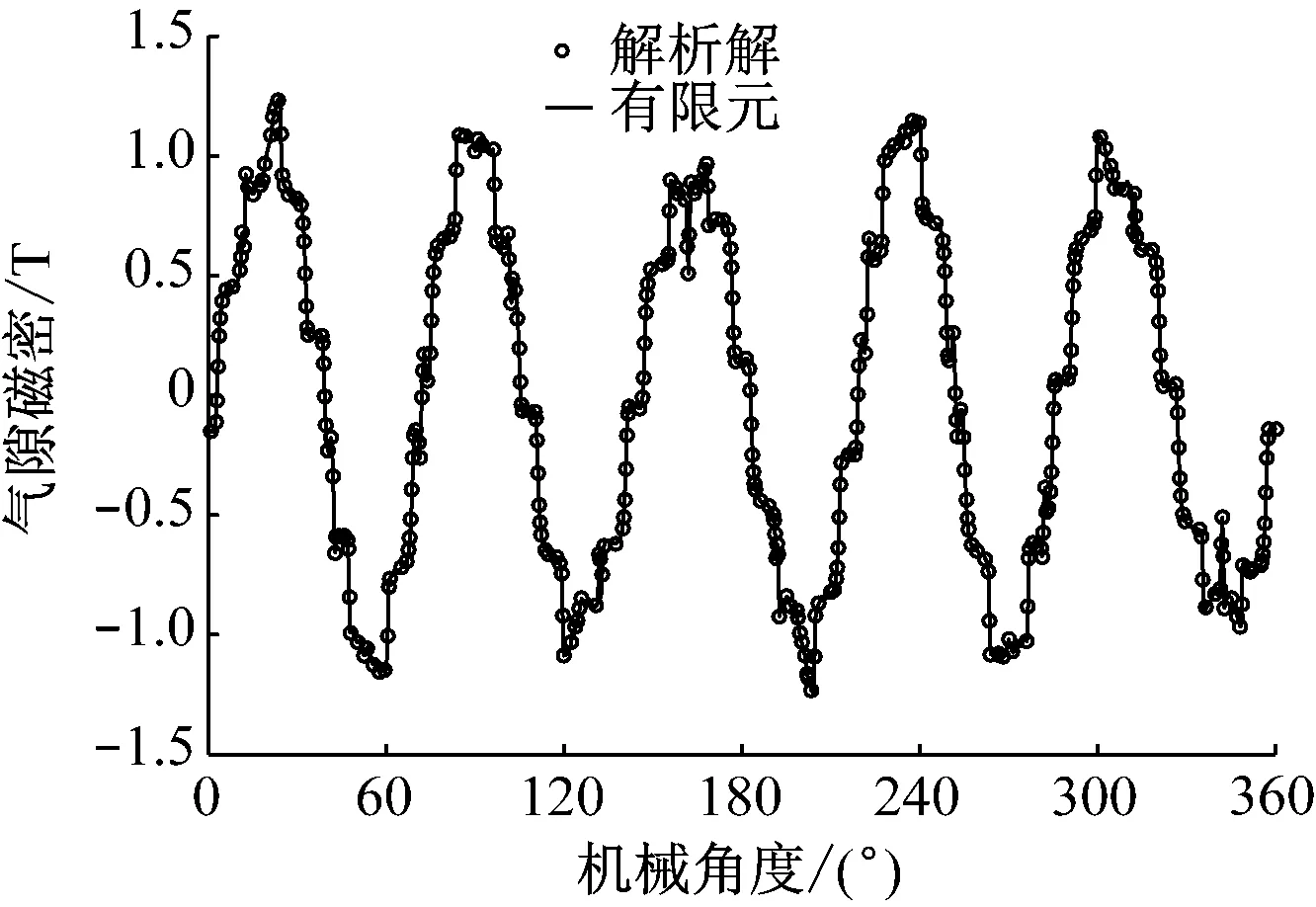
圖14 不同模型下PMSM的氣隙磁密隨機(jī)械角度變化曲線

圖15 不同模型下PMSM的電磁轉(zhuǎn)矩隨時(shí)間變化曲線
圖15所示為負(fù)載工況下PMSM的電磁轉(zhuǎn)矩解析解與有限元解的對(duì)比圖。圖15可見,PMSM的電磁轉(zhuǎn)矩波動(dòng)較大。圖16為優(yōu)化后的十字型中心部分分段Halbach PMSM和普通表貼式PMSM在負(fù)載工況下的氣隙磁密變化曲線。由圖16可見,十字型中心部分分段結(jié)構(gòu)的PMSM的氣隙磁密波形更加正弦。
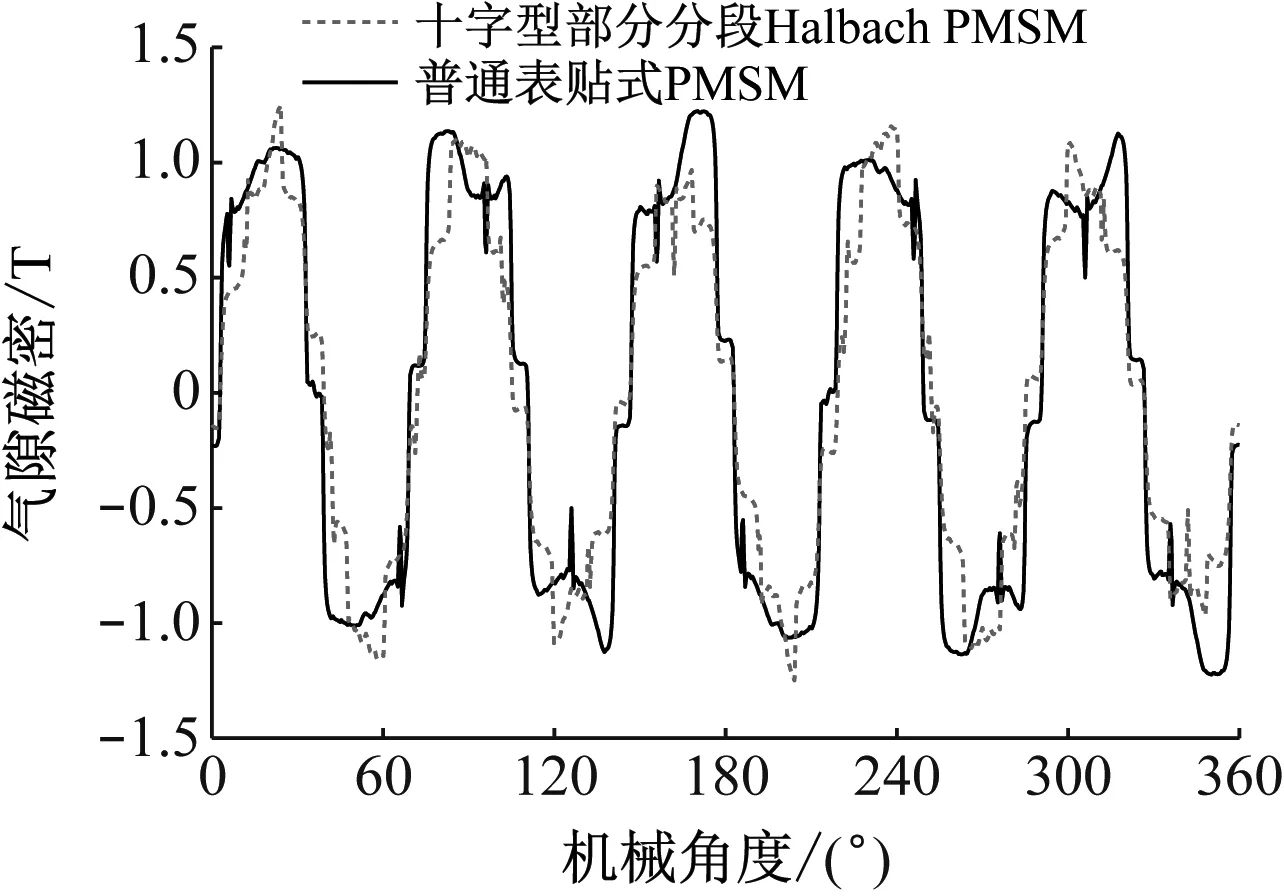
圖16 負(fù)載工況下PMSM的氣隙磁密隨機(jī)械角度變化曲線
5.3 PMSM機(jī)械強(qiáng)度分析
當(dāng)PMSM轉(zhuǎn)速為1 500 r/min時(shí),在切向離心力和電磁力的作用下,通過仿真得到PMSM的等效應(yīng)力和總變形,如圖17、圖18所示。
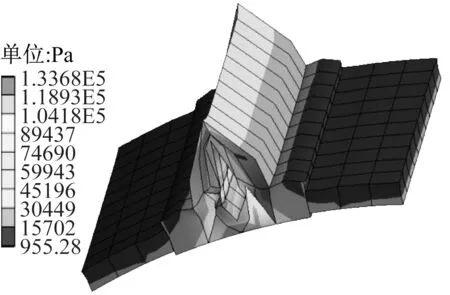
圖17 PMSM的等效應(yīng)力圖Fig.17 Equivalent stress map of PMSM
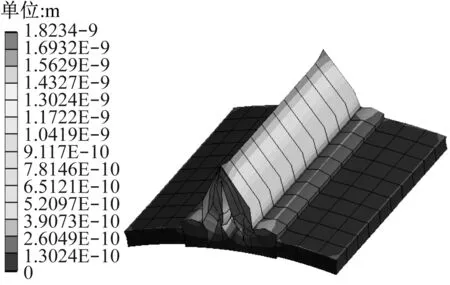
圖18 PMSM的總變形圖Fig.18 Total deformation map of PMSM
如圖17所示PMSM的等效應(yīng)力,顯示了由其切向離心力和電磁力引起的等效應(yīng)力。由圖17可見,永磁體的最大等效應(yīng)力發(fā)生在靠近轉(zhuǎn)子側(cè),其最大等效應(yīng)力為1.34×108Pa,低于永磁體拉伸應(yīng)力80 MPa。因此,永磁體離心力和電磁力引起的等效應(yīng)力不會(huì)破壞永磁體的機(jī)械結(jié)構(gòu)。如圖18所示PMSM的總變形,顯示了永磁體在切向離心力和電磁力作用下導(dǎo)致的結(jié)構(gòu)變形。由18可見,永磁體的最大變形發(fā)生在其中心切口邊緣,而發(fā)生在永磁體底面結(jié)構(gòu)變形很小。
6 結(jié)論
1) 在永磁體用量相同的情況下,十字型結(jié)構(gòu)與T型和Hat型結(jié)構(gòu)相比,對(duì)渦流損耗的抑制效果相差不大,但在降低齒槽轉(zhuǎn)矩、氣隙磁密諧波畸變率方面效果明顯。
2) 對(duì)于T型、Hat型及十字型結(jié)構(gòu),對(duì)其主磁極進(jìn)行中心部分分段增大了氣隙磁密諧波畸變率。與采用主磁極單側(cè)部分分段結(jié)構(gòu)相比,主磁極中心部分分段結(jié)構(gòu)的氣隙磁密諧波畸變率更小。
3) 十字型部分分段Halbach PMPA結(jié)構(gòu),相比于T型和Hat型部分分段結(jié)構(gòu),其幾何中心與重心重合,機(jī)械強(qiáng)度更優(yōu)。

