架設高度對牽引網阻抗矩陣值的影響分析與計算*
魏 祥,陳劍云
(華東交通大學 電氣與自動化工程學院,南昌 330013)
高速鐵路牽引供電網作為一組架空平行多導體輸電系統,其自阻抗值與互阻抗值是系統分析計算以及繼電保護整定的重要參數。在工程設計過程中,一般都采用簡化Carson 公式進行計算,該公式引入了導線—大地等值深度的概念,計算結果只與電流頻率、大地土壤導電率的大小有關,而與導線架設高度無關[1]。簡化Carson 公式在50 Hz工頻情況下,其計算精度基本滿足工程要求,但是隨著牽引網對諧波分布、電磁暫態信號傳播特性深入分析的需要,寬頻段的阻抗特性曲線也是必須獲取的基礎參數,導線架設高度對阻抗值的影響也許不容忽略,特別考慮到我國大多的高速鐵路主要架設在離地面很高的橋梁上,牽引網的架設高度差別很大,架高對牽引阻抗值的影響有多大,是個值得深入分析與研究的問題。
架空導線阻抗計算的關鍵在于求解大地的內阻抗以及導線與大地間互阻抗,這是一個非常復雜的電磁場理論分析與數值計算問題。早在1926年,Carson 和Dommel[2-3]通 過分析 半無 限 平面 大地模型的電磁場,給出了導線—大地回路的自阻抗與互阻抗的積分計算公式及其級數解,成為經典求解公式。Carson 級數解是由無窮級數構成,計算項復雜繁瑣,所謂簡化Carson 公式即是只取級數的第一項而忽略后面的高次項,級數第一項與導線架設高度無關,而高次項都相關[4]。雖然架空平行導 體 阻 抗 計 算 還 有Tylavsky[5]和Dubanton[6]等 公式,但Tylavsky 公式主要應用于隧道中牽引網阻抗計算,而Dubanton 公式形式簡單,卻誤差較大[7],所以目前仍認為Carson 公式計算較為準確有效。對于高架橋區段的牽引網阻抗計算,文獻[8]雖然結合Carson 理論但沒有計算出高架橋路段的阻抗矩陣,也沒有考慮架高對阻抗矩陣造成的影響。文獻[9]考慮到了高架橋的影響,計算出了供電回路和橋墩回路的耦合系數,但沒有涉及架高后的牽引網阻抗矩陣。對于不同土壤電阻率和諧波頻率下的架高對牽引網阻抗矩陣值造成的影響,國內外文獻還未見到對這一問題進行詳細探討。
文中以Carson 級數公式中與高度無關的第一項作為基本值,把剩余的高次項作為修正值,分析與計算牽引網架高對阻抗值的影響。通過電氣化鐵路牽引網為實例,計算給出在不同大地土壤導電率情況下的阻抗—架高特性曲線;計算不同諧波頻率下的阻抗—架高特性曲線,并分析了不同情況下架高對阻抗值的影響;根據不同情況下架高對阻抗值影響大小,從而判斷該情況下架高對阻抗值的影響是否可以忽略,最后整理出數據以供參考研究。
1 Carson 阻抗計算公式
1926 年,Carson、POLLACZEK 等 人 幾 乎 同 時解決了架空導線-地回路阻抗計算的問題[10]。計算公式如式(1)~式(4):

式中:

式中:μ0為導線導磁率,取4π·10-4,H/km;ri為導線半徑,m;hi為導線對地平均高度,m;ω為角頻率,rad/s;θ為導線電阻率,Ω·m;dij為導線i與j之間的距離,m;Dij為導線i與j的鏡像距離,m。
上述的Zg和Zgm為大地回路對于輸電線路自阻抗和互阻抗所引起的修正,由式(5)~式(12)表達:

式中:


以及
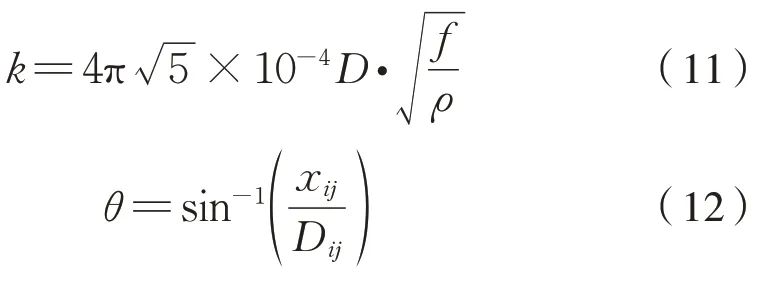
式(8)中:sign 函數每隔4 項改換符號;D在計算自阻抗時為2hi,計算互阻抗時為Dij。
在工程設計過程中,頻率f為50 Hz,計算牽引網阻抗矩陣時對大地回路阻抗Rg與Xg取第一項近似,也就推導出了簡化Carson 法,其中導線—地回路等值自阻抗[11]為式(13)~式(14):

式中:

2 條導線—地回路間的等值互阻抗為式(15):

式中:Re為導線交流電阻,Ω/km;r′為導線等效半徑,m;f為電流頻率,Hz;ρ為土壤電阻率,Ω·m;dij為兩導線間的距離,m。
2 架高相關的阻抗修正公式
由上節可知,當架空導線中通過的是50 Hz 工頻交流電時,對式(6)、式(7)取第一項來近似,也就 是 式(13)中 的0.05 和0.144 6。與Carson 法 相比,簡化Carson 法只計入了Rg與Xg第一項,計算出的阻抗值只是基本值,而大地回路阻抗Rg與Xg第一項后的多項式即為Carson 法對簡化Carson 法的修正值ΔZ,為式(16)~式(20):
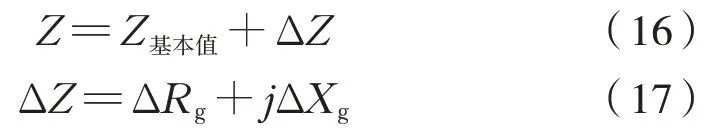
式中:

即:

結合式(11)、式(12)易得自阻抗修正ΔZii和互阻抗修正ΔZij公式,由于兩者都是關于頻率f、土壤電阻率ρ和導線對地高度h3 個變量的多元函數公式,以下將借助修正公式來分析不同土壤電阻率和諧波頻率下的架高對牽引網阻抗矩陣值的影響。
3 實例分析
3.1 牽引網空間分布結構
在AT 牽引供電系統中,承力索、接觸線以及正饋線和保護線都是同桿架設,平行于鋼軌,綜合接地線也是沿著鐵路沿線鋪設,平行于鋼軌[12]。復線AT 供電方式牽引網空間分布如圖1 所示。國內復線AT 供電方式牽引網導線空間分布結構基本上是相同的,即架高之后牽引網各導線的架設高度會整體改變,但各導線的橫向間距不變。其中,各導線型號及參數見表1。

圖1 復線AT 供電方式牽引網懸掛圖

表1 牽引網各導線型號及參數[1]
3.2 不同土壤電阻率情況下阻抗—架高特性曲線
在實際線路中,牽引網各導線中通過的單相交流電頻率為工頻,當線路鋪設高架橋跨越江河峽谷時,牽引網各導線的架設高度就會發生改變,而牽引網阻抗矩陣值與導線架設高度有關;再者,牽引網輸電線路上土壤的電阻率不是一成不變的,線路的串聯電阻、電抗易受土壤電阻率影響[7],分析工頻時不同土壤電阻率情況下架高對阻抗矩陣值的影響。
高速鐵路高架橋高度沒有專門規定,不同地形、地質條件有所差異,橋墩高度一般在數米至20 m[13],研究中考慮特殊情況,選擇高架橋高度范圍5~50 m,步長為5 m,以上行接觸導線為例,分別計算不同土壤電阻率情況下接觸導線自阻抗值、接觸導線與鋼軌的互阻抗值的修正。為了方便分析不同情況下架高對阻抗值的影響及大小,引入阻抗值修正比δ,計算公式如式(21):

式中:h為架設高度;ρ0為土壤電阻率;頻率為f0情況下第i根導線的自阻抗值(或與第j根導線的互阻抗值)。在研究不同情況下架高對阻抗矩陣值的影響時,頻率f0和土壤電阻率ρ0為常量,自阻抗(或互阻抗)修正公式ΔZii(ij)(h,ρ0,f0)就變為只與高架橋高度相關的修正公式ΔZii(ij)(h)。不同土壤類別電阻率的參考值(沙質泥土為典型值100 Ω·m[10])見表2,工頻時不同土壤電阻率情況下阻抗修正比-架高特性曲線如圖2、圖3 所示。

表2 常見土壤電阻率[14]

圖2 不同土壤電阻率情況下自阻抗值修正比—架高特性曲線

圖3 不同土壤電阻率情況下互阻抗值修正比—架高特性曲線
由圖2、圖3 可知,自阻抗值和互阻抗值的修正比δ都會隨著架設高架橋的高度增加而增加,最大可達2%,且在較高的土壤電阻率情況下,阻抗值修正比δ反而較小,基本在0.5%以下。故在不同土壤電阻率情況下,工頻時架高對牽引網阻抗矩陣響很小,可以忽略不計。
3.3 不同諧波頻率下阻抗—架高特性曲線
在實際線路中,牽引網各導線中不只含有頻率為50 Hz 的交流電,這是因為電氣化鐵路中的非線性負載在運行時會產生大量諧波,而不同次數的諧波流入牽引網輸電線路中都會對牽引網阻抗矩陣值造成影響,此節討論不同頻率下架高對阻抗矩陣值的影響。
牽引網各導線中的諧波不僅僅是3、5、7 次等低次諧波,而是20~50 次之間的甚至更高次的諧波,故諧波次數取3~99 次中各奇數次,即頻率取150~4 950 Hz,土壤電阻率為典型值。如上節所述,采用式(21)來分析不同頻率下架高對阻抗矩陣值的影響。以上行接觸導線的自阻抗和接觸導線與鋼軌的互阻抗為例,5、7、9、25、55、99 次諧波頻率下阻抗修正比—架高特性曲線如圖4、圖5所示。
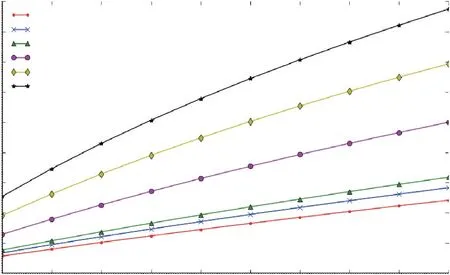
圖4 不同諧波頻率下自阻抗值修正比—頻率特性曲線

圖5 不同諧波頻率下互阻抗值修正比—頻率特性曲線
由圖4、圖5 可知,在不同諧波頻率下,自阻抗值和互阻抗值的修正比δ都會隨著架設高架橋高度增加而增加,且架高對互阻抗值的影響比自阻抗值大。在99 次的高次諧波(4 950 Hz)下,自阻抗值和互阻抗值的修正比δ最大分別可達8.75%和18.70%。具體數據見表3、表4。

表3 不同諧波頻率下自阻抗值修正比—架高數據表

表4 不同諧波頻率下互阻抗值修正比—架高數據表
由表3、表4 可知,在7 次諧波(350 Hz)下,架設高架橋高度在0~50 m 時,自阻抗值和互阻抗修正比δ基本在5%以下,即滿足實際工程需要[15],故在此頻率下架高對牽引網矩陣阻抗值的影響可以忽略。對于自阻抗而言,在頻率高于1 250 Hz時,例如55 次諧波(2 750 Hz),當架高超過30 m時,自阻抗值修正比δ大于5%,此時就需要考慮架高對自阻抗值造成的影響,而在99 次諧波(4 950 Hz)下,架高達到20 m 時就需要考慮到架高對自阻抗值造成的影響了。同理,在頻率高于1 250 Hz 時,架高超過15 m 時需要考慮架高對互阻抗值造成的影響,而在55 次諧波(2 750 Hz)下,架高達到5 m時就不能忽略架高對互阻抗值造成的影響了,其余情況都可以以此作為參照來推算,不再贅述。
4 結 論
根據Carson 理論進行分析,得出與高度相關的高次項并作為修正值,結合國內AT 牽引供電系統為實例進行計算分析,得出以下結論:
(1)當牽引網中通過工頻交流電時,架高對牽引網阻抗矩陣值造成的影響很小,在實際工程設計中是可以忽略的。
(2)當牽引網中含有諧波電流,且所含諧波的次數在7 次以下時,架高對牽引網阻抗矩陣值的影響可以忽略;當所含諧波的次數在7~25 次之間時,架高對阻抗矩陣中自阻抗值造成的影響仍可以忽略,但要考慮對互阻抗值造成的影響;當所含諧波的次數高于25 次時,架高對牽引網阻抗值的影響較大,超過了實際工程誤差允許的范圍5%,其影響不可忽略。

