地鐵設備吊掛梁瞬態沖擊仿真及試驗研究

張 宜，韋海菊

（中車南京浦鎮車輛有限公司，南京 210031）

吊掛梁用于將高壓箱、變流器、制動模塊等設備連接到底架邊梁上。吊掛梁若發生斷裂或疲勞破壞會嚴重影響地鐵安全性，因此建立準確預測結構薄弱區域的計算模型，是后續進行強度評估和優化的前提。

目前設備沖擊仿真常用靜力學方法簡化計算而不是瞬態方法，同時試驗驗證采用定性驗證而非定量驗證。例如：劉峰［1］使用瞬態法計算變流器沖擊強度，但只做了定性試驗驗證；徐聰［2］使用靜力學和瞬態方法計算了高壓箱沖擊強度，發現2 種方法結果差異較大，但未進行試驗驗證；黃磊杰［3］使用靜力學方法對變流器機箱進行沖擊強度評估和優化。

文中使用模態疊加法計算了吊掛梁瞬態沖擊的動態響應，并用試驗定量驗證了模型的準確性，最后對吊掛梁型材進行了減重優化。基本流程如圖1 所示。

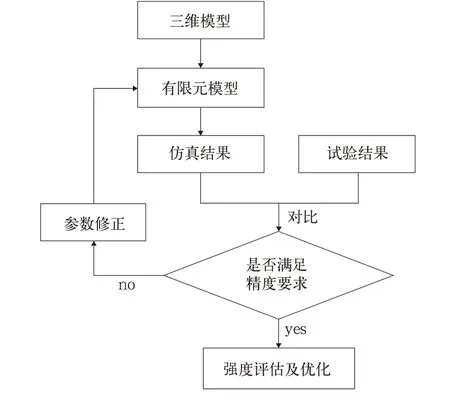
圖1 基本流程圖

1 模態疊加法基本理論

模態疊加法求解瞬態沖擊問題，首先求解系統的各階振型和對應的模態頻率，利用振型和模態頻率將運動平衡方程轉換成單自由度系統振動方程并求解動態響應，然后將每個振型響應結果進行線性疊加，得到原來系統的動態響應［4-5］。

在沖擊載荷作用下，多自由度系統運動微分方程可以表示為式（1）：

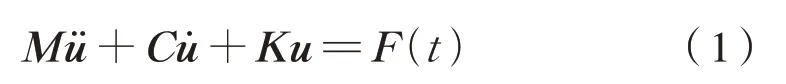
式中：M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；F（t）為外載荷矩陣；u¨ 為加速度矩陣；u˙為速度矩陣；u為位移矩陣。

由式（1）得到系統的n階固有頻率ω1，ω2，…，ωn和n階振型φ1，φ2，…，φn。

位移矩陣可表示為式（2）：

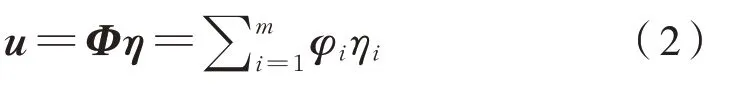
式中：Φ為振型矩陣；η為模態坐標向量；φi為振型向量；ηi為模態坐標。

將式（2）帶入式（1），并在方程兩邊同乘振型矩陣的轉置φT得到式（3）：

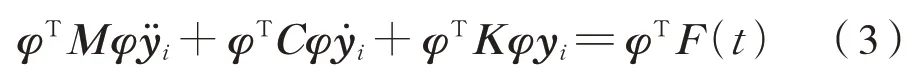
對式（3）進行求解得到主坐標下的響應，再變換得到物理坐標下的響應。通常高階模態對響應的影響很小，所以在滿足工程精度的前提下對高階模態進行截斷處理，模態截斷的頻率通常為最高激勵頻率的3～5 倍。

2 吊掛梁瞬態沖擊仿真

2.1 材料模型及參數

選擇MAT1 材料模型，材料的泊松比、彈性模量和密度等參數見表1。

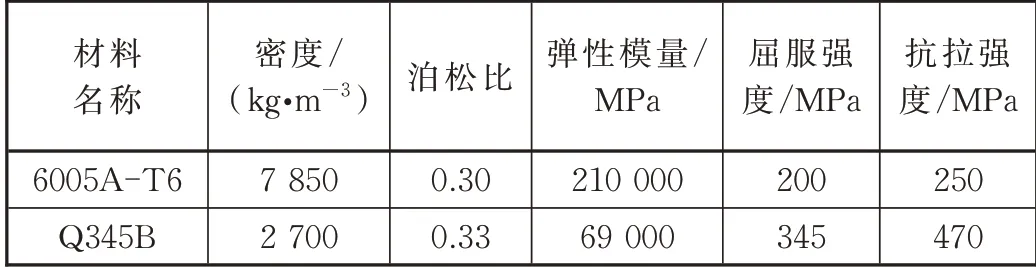
表1 材料力學性能參數

2.2 沖擊載荷

吊掛梁設計應滿足IEC 61373-2010《機車車輛設備沖擊和振動試驗》標準的要求，該標準規定直接安裝于車體下的設備屬于1 類A 級設備［6］，沖擊脈沖信號如圖2 所示。

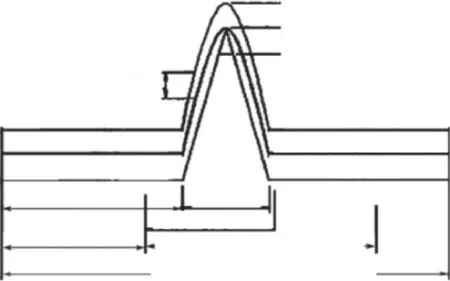
圖2 半正弦沖擊脈沖信號控制圖

對應的沖擊加速度函數應滿足式（4）：

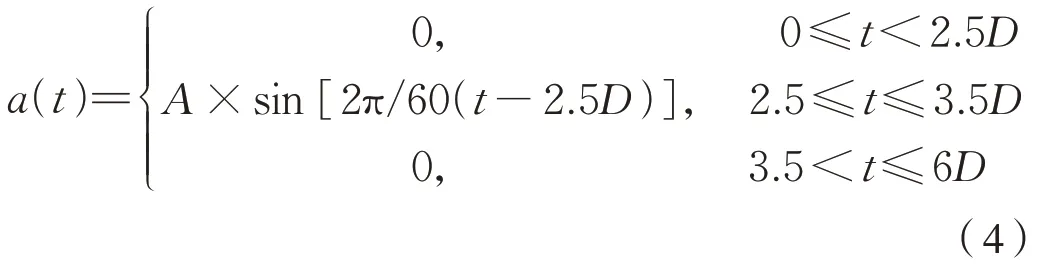
式中：A為峰值加速度，X、Y和Z方向對應的峰值加速度分別為±50 m/s2、±30 m/s2和±30 m/s2；D為沖擊時間30 ms，由于X和Y方向是對稱的，且Z正方向比負方向惡劣，文中只計算和對比正方向結果。

2.3 有限元模型

有限元模型包括吊掛梁和吊掛座、配重、工裝3 個部分。吊掛梁材料為鋁合金6005A-T6，吊掛座材料為Q345，通過鉚釘與吊掛梁連接，共重85 kg；配重材料為Q345，用于模擬車下吊掛設備，重775 kg；工裝材料為Q345，用于連接吊掛梁和試驗臺，重1 811 kg。以上結構均采用殼單元進行離散，各個部分的有限元模型如圖3 所示。

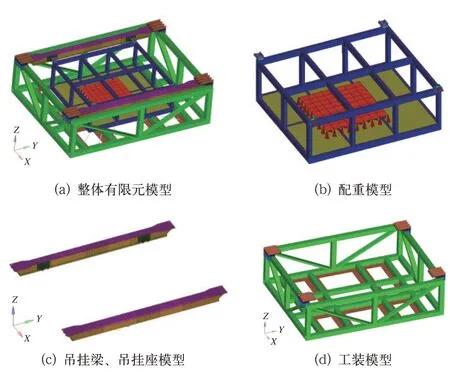
圖3 有限元模型

2.4 仿真結果

3 個方向的沖擊響應Mises 應力云圖及響應曲線如圖4～圖9 所示。

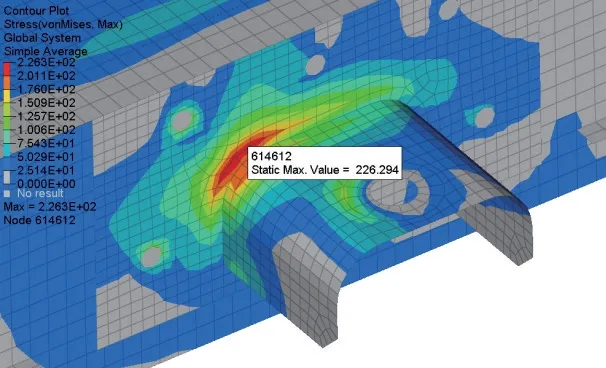
圖4 X 方向沖擊Mises 應力云圖

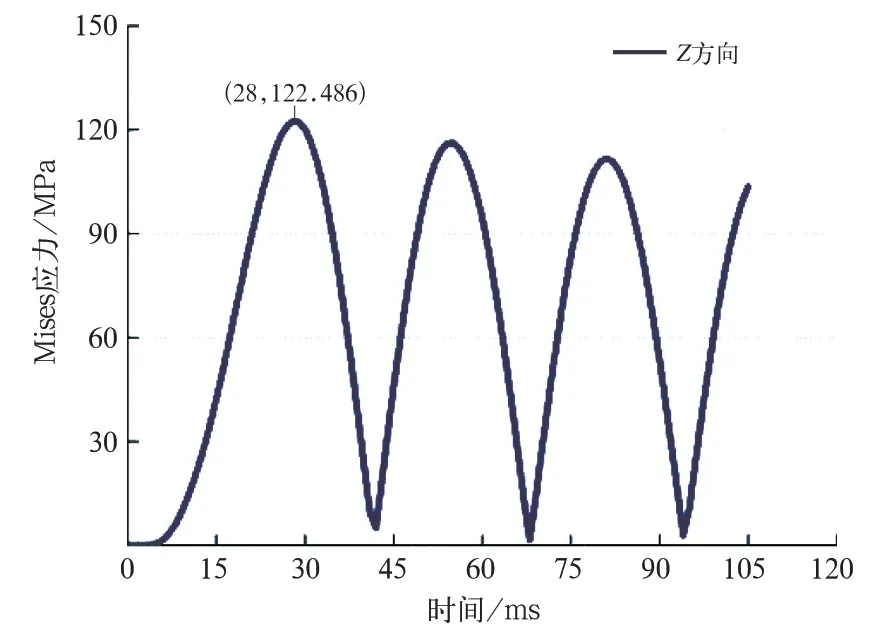
圖9 Z 方向沖擊最大位置Mises 應力曲線

X方向沖擊的最大等效應力位于吊掛座焊縫根部，在第1 個響應周期的26 ms 時Mises 應力最大，為226.294 MPa，小于Q345B 的屈服強度。在之后的響應周期，由于結構阻尼的作用，振動不斷衰減。

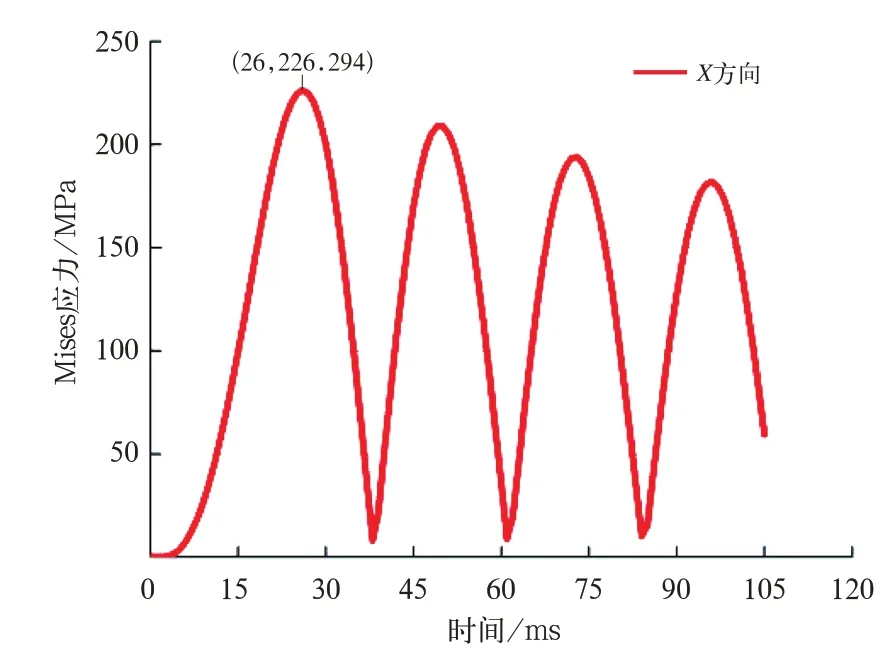
圖5 X 方向沖擊最大位置Mises 應力曲線

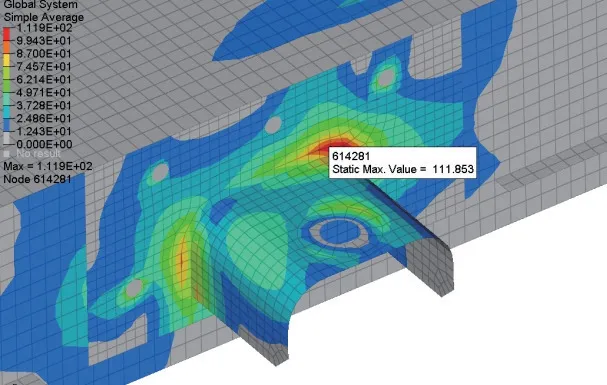
圖6 Y 方向沖擊Mises 應力云圖

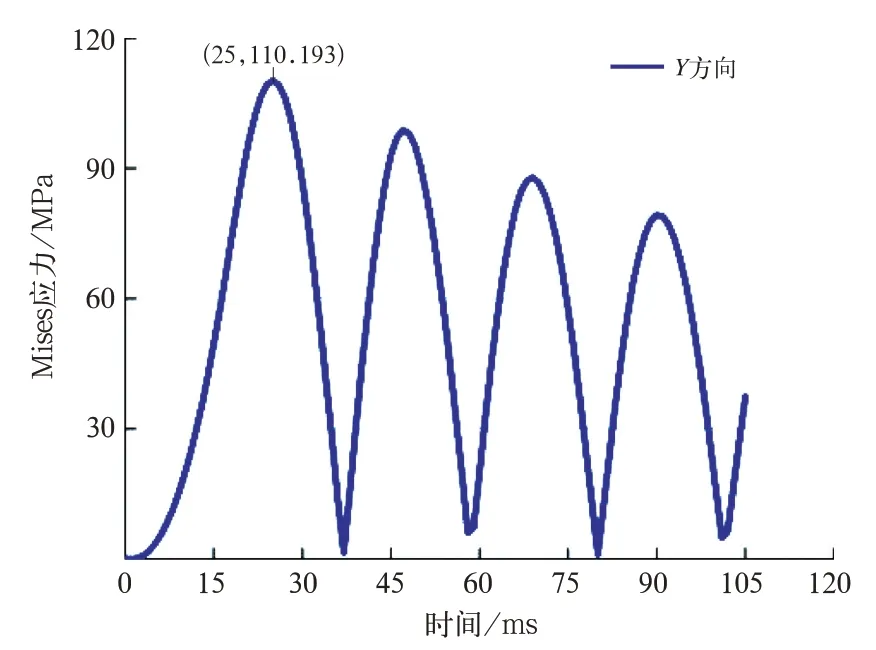
圖7 Y 方向沖擊最大位置Mises 應力曲線

Y方向沖擊的最大等效應力位于吊掛座焊縫根部，在第1 個響應周期的25 ms 時Mises 應力最大，為110.193 MPa，小于Q345B 的屈服強度。

Z方向沖擊的最大等效應力位于吊掛座焊縫根部，在第1 個振動周期的28 ms 時Mises 應力最大，為122.486 MPa，小于Q345B 的屈服強度。

由仿真結果看出3 個方向最大應力最大值都出現在第1 個響應周期內，位于吊掛座焊縫根部，該位置附近為高應力區域，可以作為試驗布置應變測點的參考點。

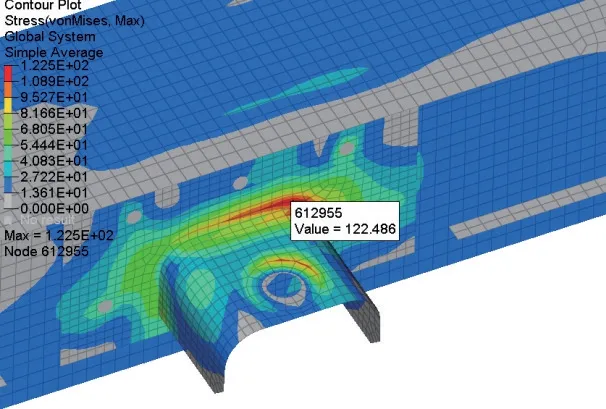
圖8 Z 方向沖擊Mises 應力云圖

3 試驗驗證

3.1 試驗設備

用于試驗的吊掛梁及相關部件已安裝到試驗臺上，如圖10 所示，試驗主要設備見表2。

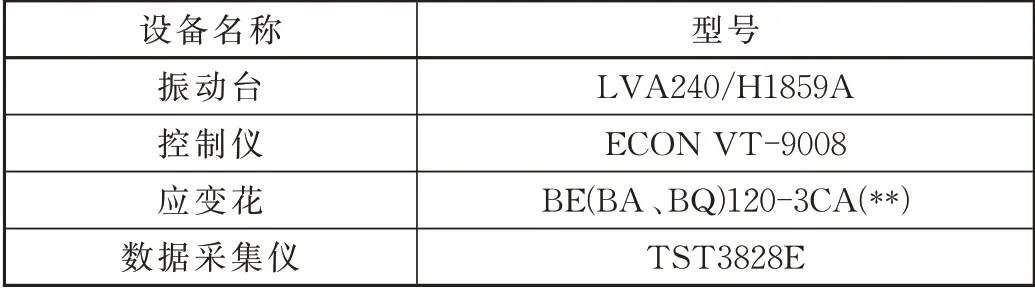
表2 沖擊振動試驗設備

圖1 0 吊掛梁沖擊振動試驗臺

根據2.4 節的仿真結果在吊掛座S3處布置1 個應變花，值得注意的是，試驗時布置的應變測點并非是最大響應所要出現的位置，而是用于監測沖擊過程的應變響應及結果驗證，測點布置如圖11所示。

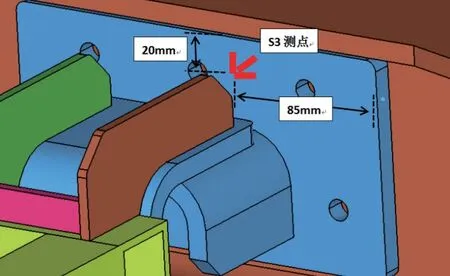
圖1 1 應變花貼片位置

3.2 對比方式

方式1：0o、45o、90o應變花采集3 軸應變，根據式（5）～式（7）計算出主應力，再根據式（8）計算出等效應力，跟仿真相同位置的Von Mises 應力對比。

方式2：0o、45o、90o應變花采集3 軸應變，選取最大通道的方向應變，根據式（7）計算出方向應力，跟仿真相同位置的方向應力對比。

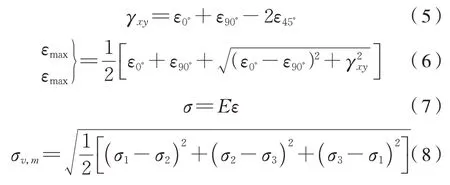
式 中：γ為 切 應 變；ε為 正 應 變；E為 彈 性 模 量；σv，m為等效應力；σi(i=1，2，3)為第i主應力。

在實際工程中，對于碳鋼和鋁合金材料，由等效應力判斷是否超出許用應力，而應力的正負方向則需要比較方向應力，因此先用方式1 對比最大等效應力，再用方式2 對比單通道的方向應力。

3.3 仿真與試驗結果對比

X、Y、Z3 個方向的試驗和仿真Mises 應力及方向應力響應曲線對比如圖12～圖17 所示。

圖12～圖17 曲線表明，受到沖擊后，仿真與試驗的等效應力響應曲線在第1 個周期內有較高的一致性，應力的大小、方向和變化趨勢基本吻合。

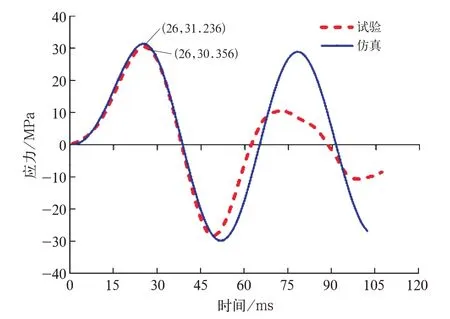
圖1 7 Z 方向沖擊的方向應力對比

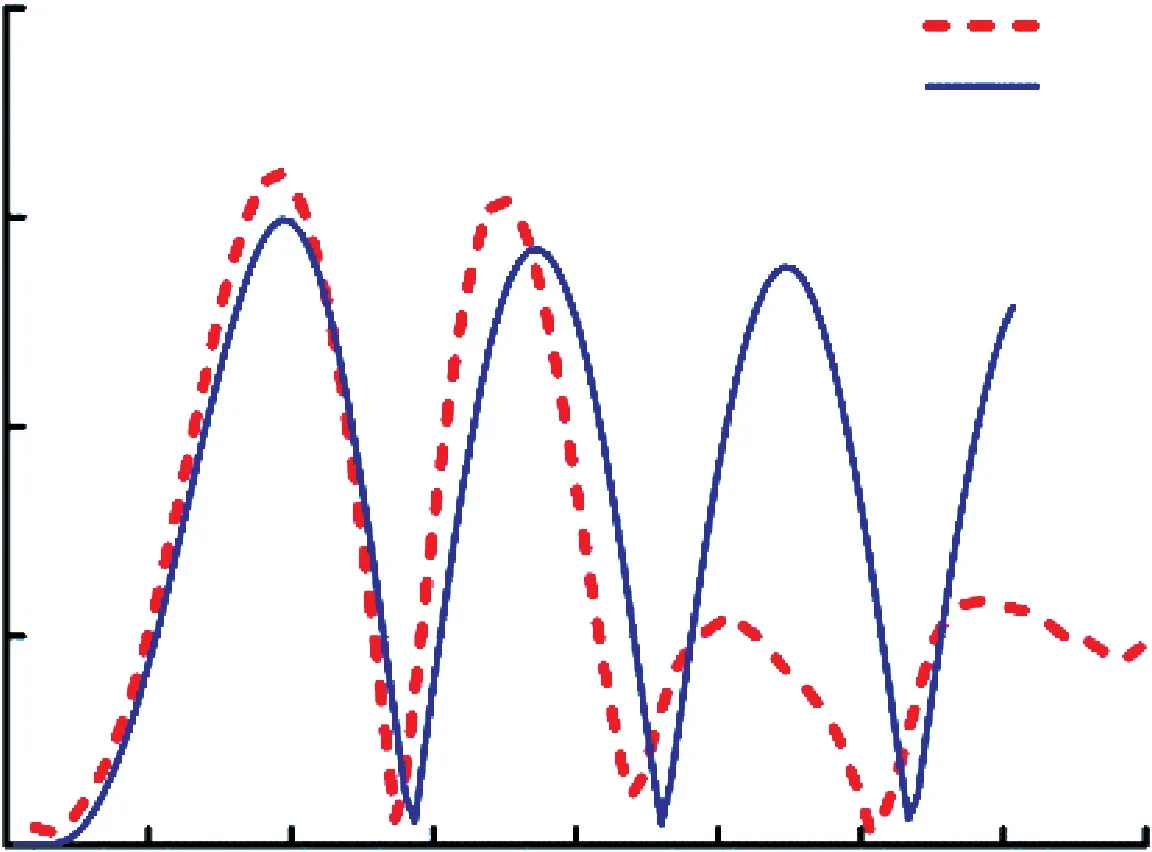
圖1 6 Z 方向沖擊的Mises 應力對比

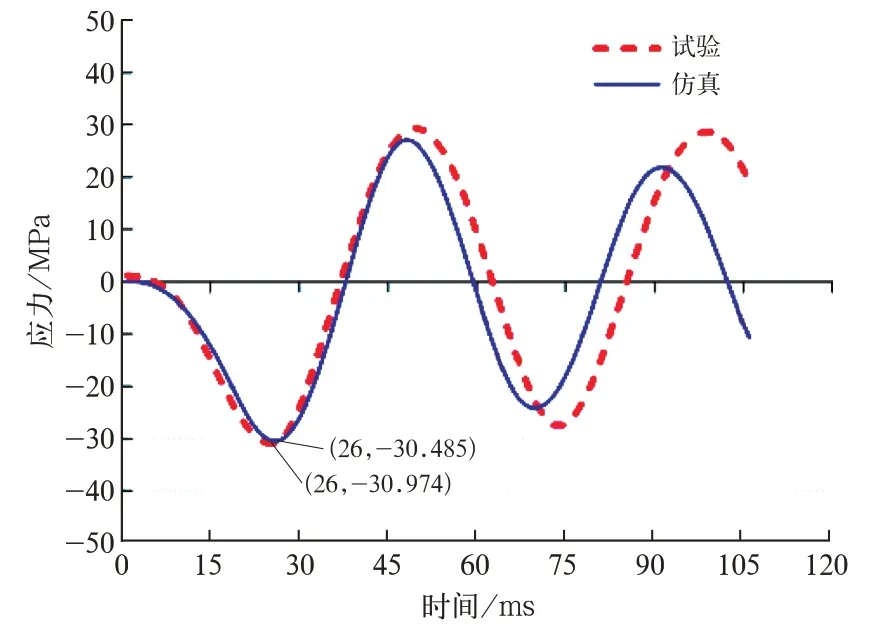
圖1 5 Y 方向沖擊的方向應力對比

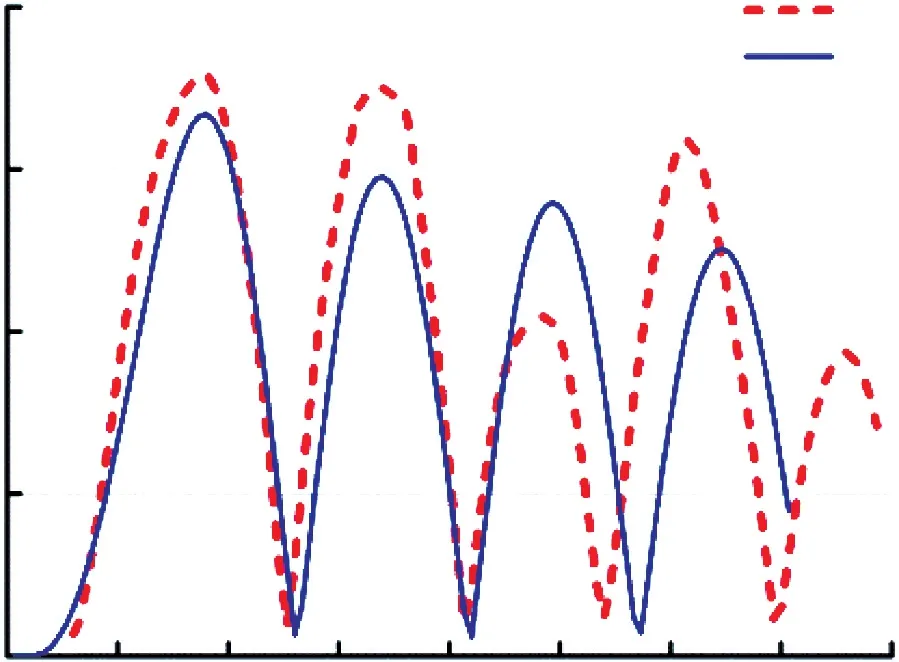
圖1 2 X 方向沖擊的Mises 應力對比

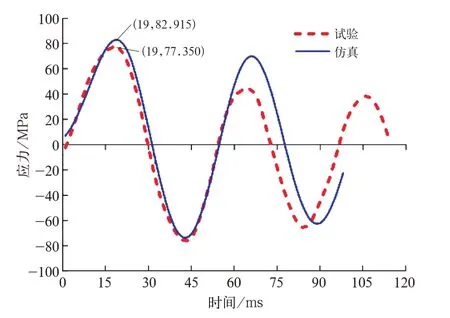
圖1 3 X 方向沖擊的方向應力對比

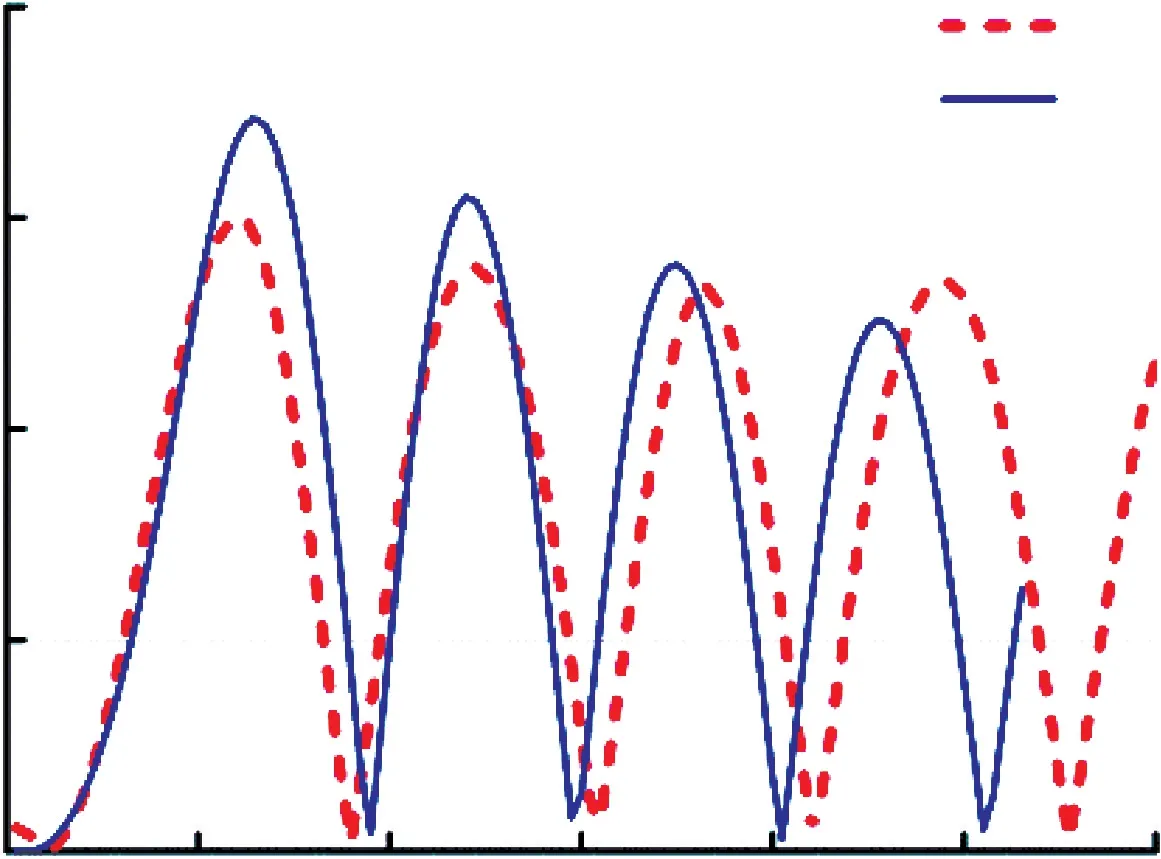
圖1 4 Y 方向沖擊的Mises 應力對比

X方向沖擊時，測點方向應力由正到負，即先受拉后受壓。

Y方向沖擊時，測點方向應力由負到正，即先受壓后受拉。

Z方向沖擊時，測點方向應力由負到正，即先受壓后受拉。

將仿真和試驗結果匯總見表3，可知第1 個響應周期內，最大誤差出現在Y方向沖擊的等效應力，為11.827%，滿足工程要求。

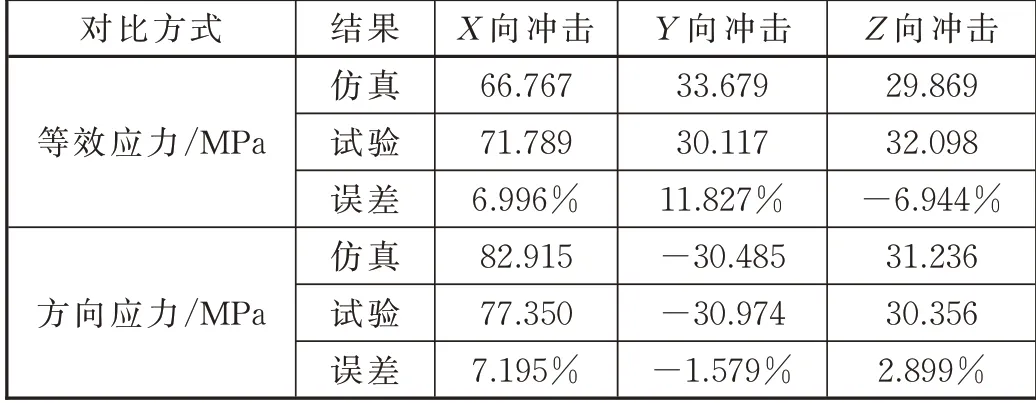
表3 仿真相對于試驗的誤差

對于第1 個響應周期后的時間，仿真與試驗有較大誤差，這可能與結構的阻尼比有關，文中采用了默認的阻尼比進行計算。

4 結構優化

4.1 型材參數優化

由第3 節可知，最大應力在安裝座區域，而鋁合金型材梁整體應力遠小于材料的屈服強度，有一定的減重優化空間。

對結構優化過程中要考慮模態頻率變化可能引起的共振現象。城軌鋁合金車體整備狀態下一階垂彎模態一般在7～11 Hz 之間，為了與車體和轉向架頻率充分隔離，應保證吊掛梁結構一階垂彎頻率不小于1.4 倍車體一階垂彎頻率［7］，即不小于15.4 Hz。

使用Optistrct 對型材進行參數優化，需要建立吊掛梁結構參數優化模型，確定設計變量、約束函數和目標函數：

（1）設計變量：吊掛梁型材截面的厚度。

（2）約束函數：X、Y、Z方向沖擊工況的最大應力≤200 MPa，一階垂彎頻率≥19 Hz。

（3）優化目標：質量（體積）最小。

型材截面的尺寸參數如圖18 所示，將這7 個板厚尺寸參數化，原始厚度為：［T1，T2，T3，T4，T5，T6，T7］=［10，8，8，8，8，10，8］，每個變量變化范圍為［3，10］，單位mm。

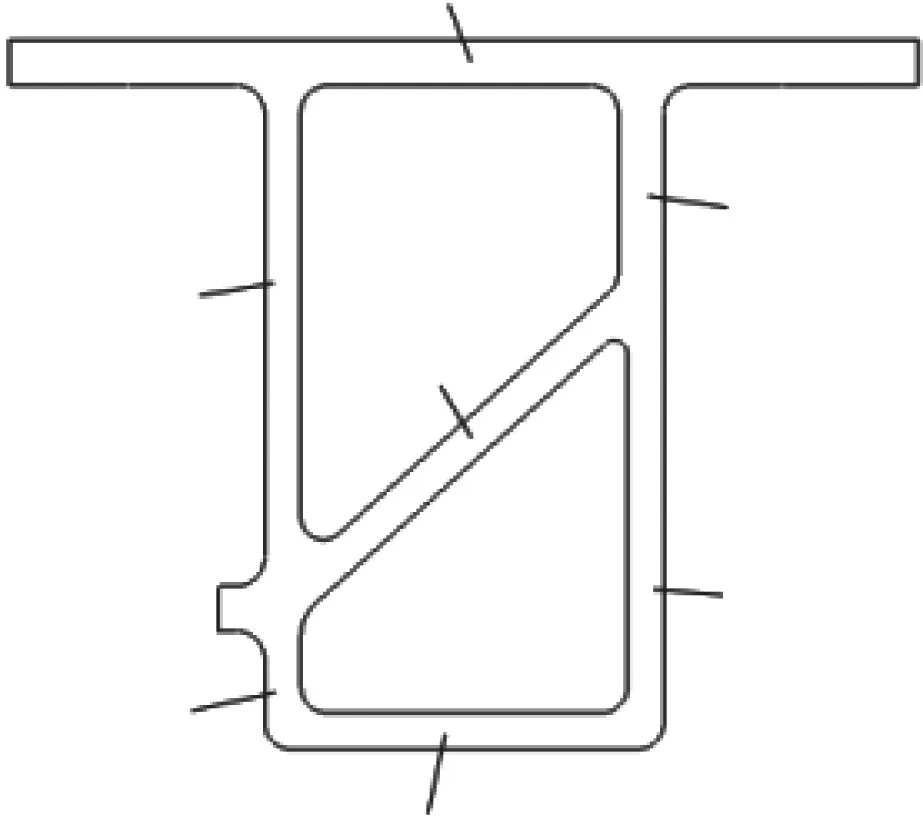
圖1 8 型材截面尺寸參數

4.2 優化結果分析

優化后各個尺寸參數的結果如下：

［T1，T2，T3，T4，T5，T6，T7］=［9，8.8，10，10，5.6，4.1，4］

對比尺寸參數的變化可知，型材在有安裝座的一側板厚有所增加，而沒有安裝座的一側板厚有所減小。厚度變化引起的響應變化見表4。

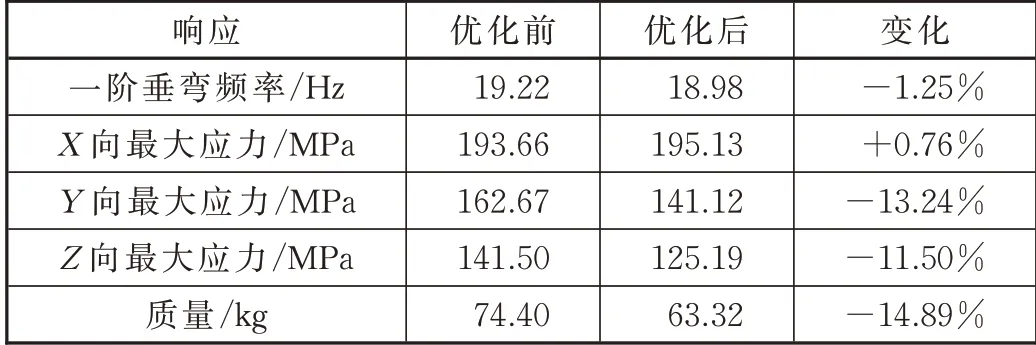
表4 優化前后各個響應的變化

分析表4 可知，優化后的3 個方向應力響應均小于材料屈服強度；一階垂彎頻率減小1.25%，略小于原始結構頻率，但仍然滿足要求；質量減小了14.89%，達到了明顯的減重效果。

5 結 語

（1）文中建立了設備吊掛梁計算的有限元模型，采用模態疊加法對吊掛梁進行瞬態沖擊仿真，獲得了吊掛梁和吊掛座高應力區域，用于指導試驗應變片貼片位置。

（2）對吊掛梁模型進行定量試驗，分別對比了仿真和試驗的等效應力和方向應力的響應曲線，仿真計算的應力大小、方向和變化趨勢與試驗有很好的一致性，表明建立的有限元模型的有效性。

（3）對吊掛梁型材結構進行參數優化，優化后的結構質量減小了14.89%，而一階垂彎頻率和沖擊強度仍然滿足要求，達到了輕量化的目的。為同類設備的沖擊仿真、試驗對標及優化提供了參考。