水下相關組件單棒轉移機械手的軌跡規劃與控制

張斌，陳建文，冷慧玲，祝沛楨

（核動力運行研究所，武漢 430200）

0 引言

核電機組的長期運行會產生大量廢棄的燃料相關組件，廢棄的燃料相關組件存放于乏燃料池中，而乏燃料水池可用的有效空格架數量有限。為了最大限度地減小相關組件的貯存空間，研制并應用水下立式縮容處理機器人對相關組件進行縮容處理[1]。縮容機器人的液壓剪切機構在水下剪切相關組件單棒，剪斷的單棒需要通過單棒轉移機械手進行轉移和分類存儲。

相關組件具有一定的輻照劑量，縮容工藝需通過水屏蔽，在水下進行縮容作業，單棒轉移機械手在操作單棒時會受流體作用力影響。單棒在水下的運動問題屬于圓柱繞流[2]問題，一方面繞流阻力會限制單棒的運動速度，另一方面單棒運動可能產生流致振動[3]，會影響單棒轉運的穩定性和可靠性。

針對單棒轉移機械手在水下操作存在的問題，本文對單棒轉移機械手的末端軌跡規劃進行研究并設計機械手控制系統確保機器人的平穩運動，實現縮容工藝中單棒轉移機器手的穩定搬運和存儲。

1 系統結構及參數

單棒轉移機械手是水下立式縮容處理機器人的組成部分之一。水下立式縮容處理機器人系統整體位于乏池水下約10 m水深環境中，其中水體溫度約為50 ℃。立式縮容處理機器人系統組成包括液壓剪切機構、組件旋轉機構、存儲容器傾斜機構、組件連接柄轉移機械手和單棒轉移機械手等。液壓剪切機構用于剪切相關組件單棒，其刀具位置可調整，組件旋轉機構用于旋轉燃料組件，容器傾斜機構用于傾斜存儲容器，可調整其傾斜角度，連接柄轉移機械手用于轉運燃料組件上方連接柄，具有2個移動自由度。單棒轉移機械手用于夾持并穩定轉運單棒，具有3個移動自由度和1個夾持自由度。水下立式縮容處理機器人整體如圖1所示。

圖1 水下立式縮容處理機器人

單棒轉移機械手結構如圖2所示。機械手共有4個關節，升降關節用于驅動機械手整體在垂直方向的升降；旋轉關節用于驅動機械手在水平面上旋轉，伸縮關節驅動機械臂在水平面上進行伸長和收縮，夾持關節為機械手爪，用于護持和夾持單棒。

圖2 單棒轉移機械手

4個關節均通過直流伺服電動機驅動，機械手升降關節、旋轉關節和伸縮關節的運動直接確定了其末端位置。各個關節的相關參數如表1所示。

表1 單棒轉移機械手關節參數

2 建模分析

為解決單棒轉移機械手在水下操作單棒的問題，需建立單棒轉移機械手的正、逆運動學模型和微分運動學模型，用于對機械手進行末端軌跡規劃和運動控制。同時需建模分析水流對單棒運動造成的阻力和振動影響，設計的控制器需在水流影響下保持穩定性。

2.1 運動學模型

根據單棒轉移機械手的結構參數，對其進行運動學分析。夾爪末端坐標用向量X表示，3個電動機角度用向量q表示，采用幾何法，根據單棒轉移機械手的結構特點進行分析，則有X=T（q），其中：

2.2 微分運動學模型

將X=T（q）兩邊微分，單棒轉移機械手的微分運動學方程可寫成δX=J（q）δq，由T（q），可計算J（q）如下：

J（q）表示單棒轉移機械手操作空間與關節空間的速度轉換關系，為機械手的速度雅可比矩陣，J（q）T表示單棒轉移機械手操作空間與關節空間的力、力矩轉換關系，為機械手的力雅可比矩陣。

2.3 單棒繞流阻力模型

單棒轉移機械手夾持相關組件單棒在水下運動時，機械臂和單棒均會受到水體作用力的影響。機械臂結構健壯，水體作用力對其干擾作用不大，而單棒整體呈細長棒狀，通過一個夾持點被機械臂夾持，受水流影響可能會產生彎曲或夾持脫落，需對單棒受水體作用力模型進行分析。

單棒在乏池的運動過程屬于典型的繞流問題，水體與單棒的相對運動會產生繞流阻力，根據繞流公式，計算繞流阻力、繞流升力和流致振動頻率：

式中：FD為繞流阻力；FL為繞流升力；f為繞流升力的脈動頻率；CD為繞流阻力系數；CL為繞流升力系數；Sr為斯特勞哈數；CD、CL、Sr與雷諾數Re有關；ρ為水流密度；v為單棒相對水池的運動速度；d為單棒直徑；A為單棒在垂直于運動方向平面上的投影面積。

計算單棒運動時的雷諾數：

式中：μ為流體動力黏性系數；L為流場特征長度。

3 軌跡規劃與控制

3.1 軌跡規劃

為使單棒轉移機械手在水下操作單棒時具有較好的穩定性和運動平穩性，在軌跡規劃時需考慮運動速度與水體繞流阻力的關系，選擇合適的運動速度，兼顧轉移效率和穩定性。同時為保證夾持的可靠性，轉移軌跡的位置、速度、加速度應連續且變化平緩。

貝塞爾曲線[4]軌跡一定經過起始點P0和終點，軌跡處處連續，且其導數仍為貝塞爾曲線，用貝塞爾曲線規劃的軌跡，其位置、速度、加速度連續且變化平緩。采用貝塞爾曲線規劃運動軌跡，通過標定與示教設置控制點，確保機械手運動軌跡符合要求。

設軌跡規劃時給定了n個控制點P0、P1、P2…Pn，其貝塞爾曲線的一般表達式可寫為

式中：CP0為初始狀態時機械臂末端坐標；CP5為機械臂的目標位置。根據各控制點，生成的機械臂末端軌跡如圖3 所示，機械臂升降、旋轉、伸縮關節的位置和速度規劃 如 圖4、圖5、圖6所示。

圖3 單棒轉移機械手臂末端運動軌跡

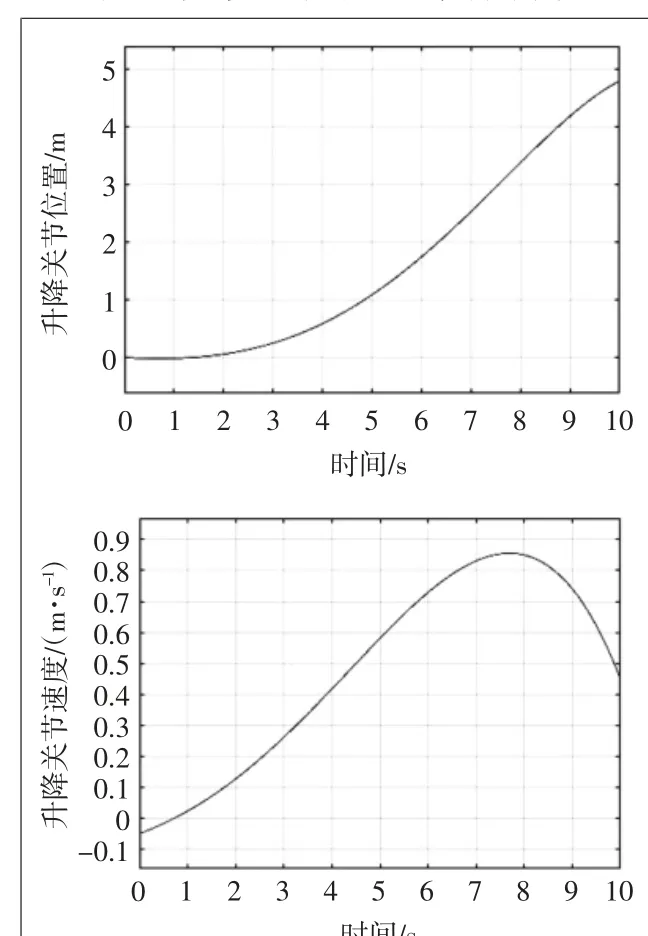
圖4 升降關節規劃位置和規劃速度

圖5 旋轉關節規劃位置和規劃速度

圖6 伸縮關節規劃位置和規劃速度

3.2 控制系統結構

為避免繞流阻力對單棒轉移機械手臂的運動產生不利影響，采用前饋控制的思想，通過前饋補償繞流阻力[5]，在較大程度上消除機械手臂運動過程中的繞流阻力的影響。同時為提高控制系統抵抗外部干擾的能力，采用PD控制算法[6]對機械手臂末端位置進行控制。

設計帶前饋控制的控制率u計算公式為

控制系統框圖如圖7所示。

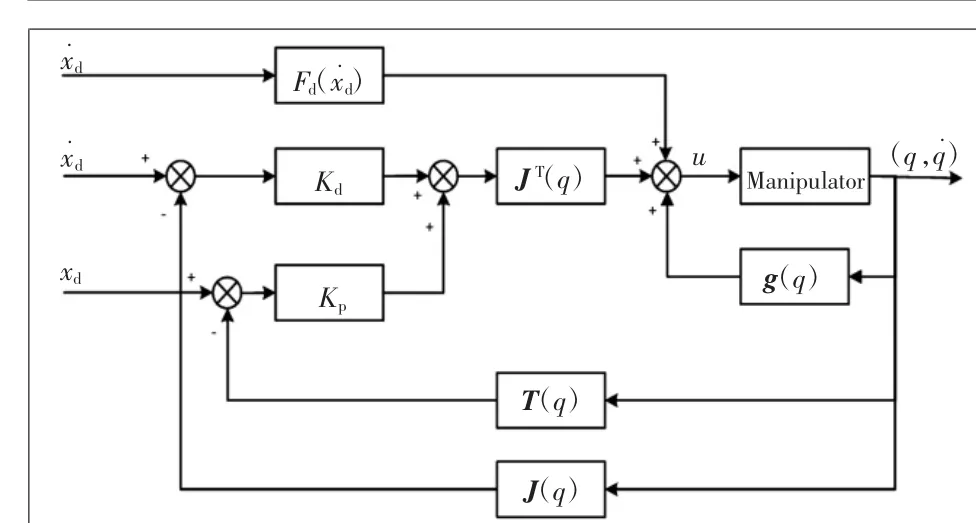
圖7 控制系統框圖

4 仿真分析

為確保單棒轉移機械手軌跡規劃和控制算法的有效性，采用仿真分析對機械手的運動軌跡和控制算法進行驗證并優化。

仿真計算平臺為Matlab 2019，采用Simulink完成規劃和控制算法，采用Simscape模塊進行物理仿真和三維可視化驗證。

4.1 仿真模型

搭建Simscape仿真模型如圖8所示，三維可視化效果如圖9所示，模型的輸入為各關節電動機力/轉矩，模型輸出為各關節當前位置和速度，且添加了外部繞流阻力和繞流升力作用。

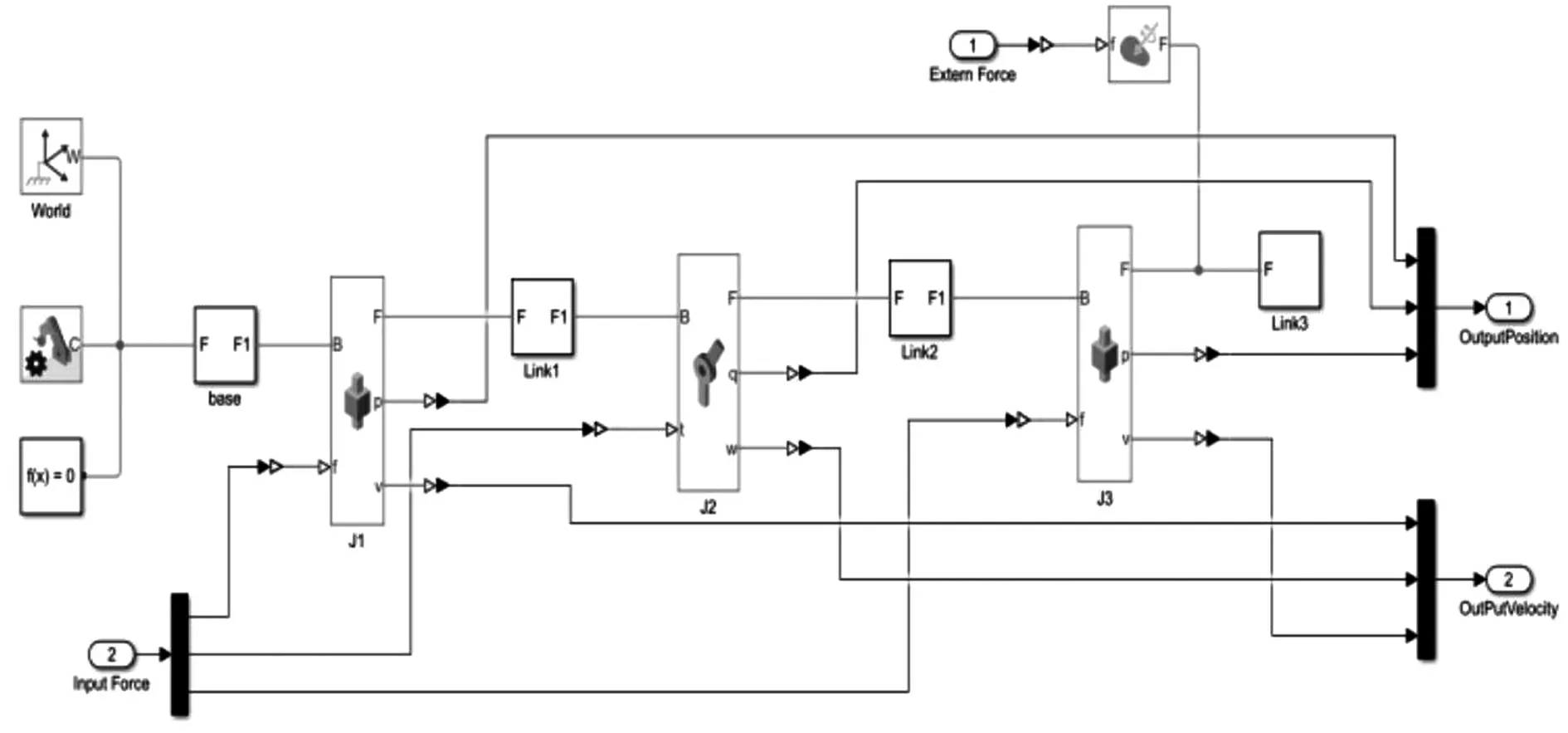
圖8 Simscape單棒轉移機械手仿真模型

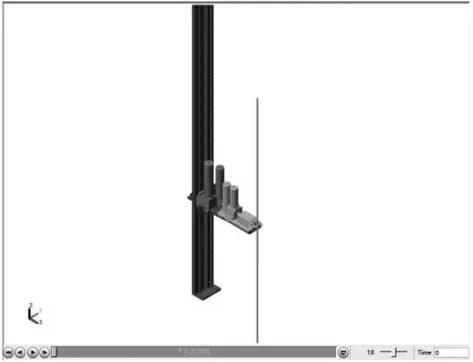
圖9 Simscape單棒轉移機械手三維可視化

根據Simscape模型，在Simulink中構件控制系統如圖10所示。其中，PD位置控制器模塊的輸入為貝塞爾軌跡，輸出為各關節力/力矩。繞流力補償模塊根據規劃速度計算了繞流力對應的力/力矩補償值，流體作用力計算模塊根據單棒運動速度計算了實時的繞流阻力和繞流升力，并將其作用于Simscape模型中。

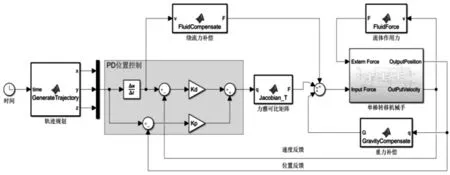
圖10 Simulink單棒轉移機械手控制系統

4.2 運動控制仿真

為驗證單棒轉移機械手運動控制系統的有效性，對機械手的各關節進行了關節位置跟蹤仿真，跟蹤信號為正弦信號，其升降、旋轉、伸縮關節的跟蹤效果如圖11、圖12、圖13所示。由運動控制仿真結果可知，位置跟蹤精度較好，具有輕微的滯后，滯后時間約為0.05 s。

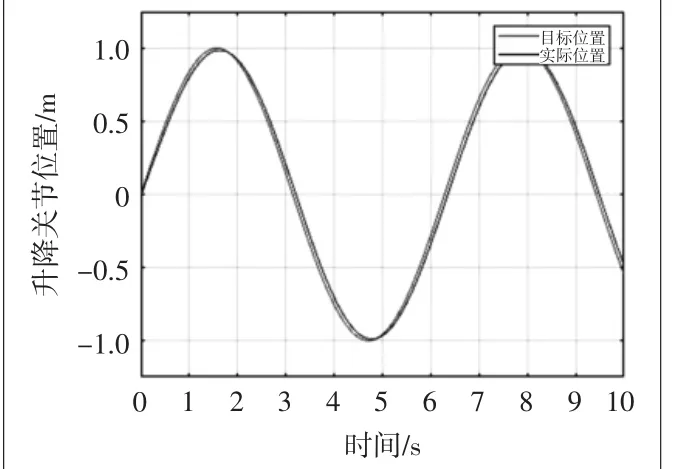
圖11 升降關節正弦跟蹤

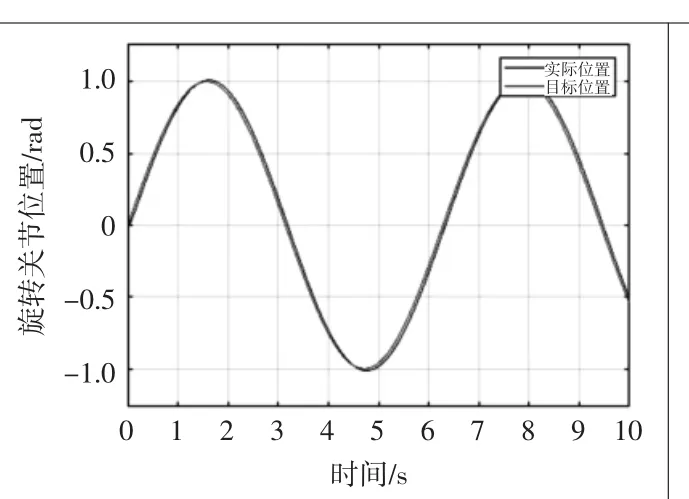
圖12 旋轉關節正弦跟蹤

圖13 伸縮關節正弦跟蹤

4.3 繞流作用力仿真

單棒在水下運動速度的不同，水體對單棒的作用力也不同，為選取合適的單棒運動速度，對不同速度下的單棒繞流阻力、繞流升力和流致振動頻率進行了仿真研究，取單棒的運動速度范圍為0～5 m/s，仿真結果如圖14、圖15、圖16所示。可以看到在低速時繞流阻力和繞流升力很小，隨著速度增大繞流阻力和繞流升力呈平方關系迅速增大，振動頻率呈比例關系逐漸增大。

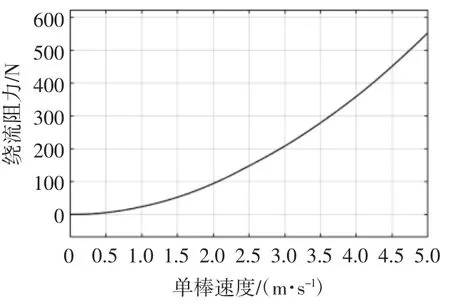
圖14 繞流阻力-速度

圖15 繞流升力-速度圖

圖16 流致振動頻率-速度圖

4.4 綜合仿真

根據規劃的機械手末端軌跡，采用帶前饋補償的PD控制器對單棒轉移機械手進行控制，計算單棒運動過程中繞流作用力，并將作用力施加在單棒上，進行單棒轉移機械手運動的綜合仿真，機械手各關節軌跡跟蹤效果如圖17、圖18、圖19所示。單棒運動過程中繞流阻力、升力和流致振動頻率如圖20、圖21、圖22所示。

圖17 升降關節規劃軌跡跟蹤圖

圖18 旋轉關節規劃軌跡跟蹤圖

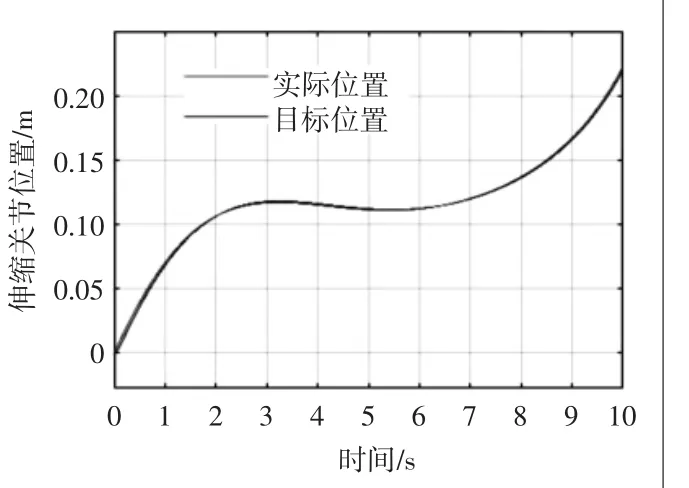
圖19 伸縮關節規劃軌跡跟蹤圖

圖20 單棒擾流阻力圖

圖21 單棒擾流升力圖

圖22 單棒流致振動頻率圖

根據仿真結果，帶前饋補償的PD控制器對機械手的控制具有較好的效果，跟蹤誤差和時間滯后都很小，驗證了帶補償的PD控制器的控制效果。機械手在按照規劃的軌跡運動時，其受到的繞流阻力最大為0.3 N，最大繞流升力為1.7×10-2N，最大振動頻率為2.8 Hz。表明規劃的軌跡沒有引起明顯繞流作用力，對單棒的轉運具有較好的效果。

5 結論

本文針對相關組件水下立式縮容工藝中單棒水下轉移問題，提出一種采用貝塞爾曲線進行軌跡規劃的方法，并設計了帶繞流阻力前饋的PD控制算法，用于機械手末端的運動控制。通過機械手運動仿真驗證了規劃的軌跡方法在位置、速度、加速度上均連續，單棒運轉平穩，同時也驗證了控制算法可有效補償繞流作用力，具有較好的穩定性和可靠性。

在后續的研究工作中，可進一步優化單棒的運動速度，在轉運效率和穩定性的約束條件下研究機械手的最佳轉運速度，同時可進一步研究單棒運轉中的流致振動問題，設計穩定性、魯棒性更佳的控制系統，并通過試驗研究進行驗證和優化。