面向三維球體空間溫度場的對射式超聲波測量研究

梅 勇，劉 暢，袁宇鵬，3，張祖偉，3，張語哲

(1.中電科技集團重慶聲光電有限公司，重慶 401332；2.中國電子科技集團公司第二十四研究所，重慶 400060；3.中國電子科技集團公司第二十六研究所，重慶 400060)

0 引言

溫度是一個表征物體或環境冷熱程度的物理量，溫度參數的測量在航空航天[1]、公共安全[2]、智能制造[3]、智能家居[4]、智能汽車等方面具有舉足輕重的地位。按照測量方式劃分，溫度測量可分為接觸式測量與非接觸式測量兩類。接觸式溫度測量器件主要有金屬溫度計、電阻溫度計、熱敏電阻等[5]，而非接觸式溫度測量器件主要有輻射測溫儀。其中，接觸式溫度測量器件盡管靈敏度和精度較高，但大部分屬于單點接觸測溫的工作方式，且對于惡劣環境的適應能力較差；而紅外輻射測溫儀是非接觸式溫度測量器件的主流產品，但也僅可探測物體表面的溫度，使用范圍受到極大制約。

針對傳統接觸式溫度測量方式和紅外輻射測溫方式存在的不足[6]，近年來發展了一種超聲波式的溫度測量方法。超聲波式溫度測量法具有非接觸式，溫度測量范圍廣，響應速度快和測量準確度高等特點，故而備受國內外學者和研究機構的廣泛關注。歐美等國在超聲波測溫領域發展領先。美國SEI公司研發了Biolerwatch系列的超聲波式溫度傳感裝置[7]，并在大型火力發電公司的核心設備鍋爐中進行了應用，實現了對溫度300～2 700 ℃的有效測量。英國CODEL針對大型煙氣管道研制出的超聲波式溫度測量系統，其應用效果良好[8]。國內對超聲波測溫領域的研究起步較晚，但近年來研究也取得了一些成果。沈雪華等[9]采用收發分體的超聲波換能器實現了二維溫度場的重建，以及在室溫無加熱、單峰對稱及單峰偏斜3種溫度場分布形態下的有效溫度測量。許琳等[10]搭建了一套基于超聲波原理的溫度測量系統，并在某型號航空發動機的主燃燒室進行應用驗證，實現了對超高溫度的長期連續測量。但現有研究主要針對二維斷面，甚至單點的溫度測量，而在三維空間方面的溫度場解算與重構方面還存在不足。

本文以一類三維球體空間溫度場的測量為例，設計了經緯方向的超聲波換能器三維拓撲結構，提出了基于徑向基神經網絡算法和奇異值分解的空間溫度重構策略，并通過仿真與實驗的方式進行了驗證。驗證結果表明，本文提出的超聲波換能器結構布設方法和溫度重構策略可精確測量三維球體空間溫度場分布。

1 超聲波式溫度測量原理與結構設計

根據超聲波在介質中的傳播速度與介質的溫度存在關聯關系的原理，發展出超聲波式溫度測量方法[11]。

根據波動理論，理想氣體介質中聲波的傳播速度與氣體介質溫度的對應關系為

(1)

式中：T為理想氣體溫度；m為理想氣體的摩爾質量；R為理想氣體的普適常數；γ為理想氣體的絕熱指數。由式(1)可見，針對特定的單一種類氣體或確定種類的混合氣體而言，參數m、R和γ為定值，因此，聲波的傳播速度與理想氣體的溫度為單值相關函數，這為基于聲速測量的超聲波測溫提供了理論依據。

1.1 二維圓面上的超聲波測溫拓撲結構

典型超聲波測溫裝置可分為點-面式和點-點式兩類。針對三維球體的橫截面方向上的布局如圖1所示。其中，圖1(a)表示收發同體的超聲波換能器在反射面上的超聲波路徑傳播形式，圖1(b)表示單個發射換能器和單個接收換能器組成的超聲波路徑傳播形式。

由圖1可見，基于收發分體超聲波換能器在圓環的平面結構上布局時，圓心附近的超聲波束較少，難以反應中心區域的溫度變化情況；而基于收發同體超聲波換能器的結構時，以45°為一個劃分區域，共8個收發同體換能器可以完成整個圓形區域的遍歷，用于飛行時間測量的往返波束達28組，對圓形區域內各劃分區域的溫度測量形成有益效果。

1.2 三維球體上的超聲波測溫拓撲結構

基于上述二維平面的布局情況，進一步設計三維球體上超聲波換能器的基本結構，如圖2所示。與二維平面的布置思想相同，以45°為一個劃分區域，共26個收發同體換能器可以完成整個三維球形區域的遍歷，用于飛行時間測量的往返波束達325組，對球形區域內各劃分區域的溫度測量形成了有益效果。

2 分時輪訓超聲波換能器接收控制流程

完成上述二維圓面和三維球面的換能器空間布局設計后，為了能夠實現對平面和球體空間進行遍歷，設計了分時輪訓超聲波換能器接收控制算法流程，如圖3所示。為了便于描述，定義超聲波換能器的序號為TR1,TR2,…,TRM，其中M為超聲波換能器的最大序號(二維圓面M=8，三維球體M=26)。圖中定義i=(1,2,…,M)、j=(1,2,…,M)分別為控制對應序號的超聲波換能器發生超聲信號和接收超聲信號，并根據發生和接收信號的時間進行平面和空間的溫度場回溯。

3 三維球體溫度場反演算法

完成超聲波換能器的空間拓撲結構設計與分時輪訓的收發流程設計后，需要進一步開展空間溫度場反演策略的研究。超聲溫度場反演是指根據超聲波信號在空間區域中的傳播速度分布以及飛行時間積分，反向推導出空間區域溫度場的過程，在需要非接觸式溫度測量領域具有重要地位。

根據式(1)可知，v2與介質溫度存在正比關系。固定超聲波換能器的布置位置后，超聲波的飛行距離將保持不變，這條超聲路徑上的飛行時間τLn可以通過積分的形式表示為

(2)

(3)

式中：n=(1,2,…，N)為第n條超聲波路徑(二維平面空間N=28，三維球體空間N=325)；x，y，z分別表示第n條超聲波路徑三維空間坐標；Ln為第n條超聲波路徑的距離。對于已經完成空間布置的超聲波換能器溫度測量系統，Ln為已知值。

實際條件下，由于超聲波換能器的布置數量有限，無法對三維空間區域進行無限劃分。因此，通過網格化方法將待測區域劃分成P個小區塊，同時通過徑向基函數的形式表示超聲波的傳播速度導數[12]：

(4)

式中αi為擬合因子，通過采集到的超聲波飛行時間可以反向推導計算，表征與超聲波飛行速率相關的分布特征。徑向基中心(xi,yi,zi)和待測值(x,y,z)表示為

(5)

聯立式(3)、(5)可得：

(6)

根據式(1)可將三維空間區域內的溫度場同樣表征為與空間坐標相關的函數：

(7)

式中形狀參數A表示徑向基函數。

聯合計算式(6)、(7)即可完成三維空間區域內的溫度場反演問題求解。

4 仿真驗證

為了對本文提出的二維圓形平面和三維球體空間的超聲波溫度場反演方法進行驗證，分別對二維圓形平面和三維球體空間開展仿真驗證。

針對超聲波溫度場反演方法的仿真結果進行定性和定量的評價和表征問題，本文引入等溫線圖和誤差分析兩個概念來分別定性和定量地描述系統誤差。其中等溫線圖是對待測區域進行溫度場反演后繪制的溫度分布圖，通過不同顏色分布表征不同的溫度差異。誤差分析中采用平均相對誤差絕對值?和均方根誤差ζ表示：

(8)

(9)

式中：b為待反演的溫度場被劃分區域數的數量；TMk、TRk分別為二維圓形對應區塊(xi,yi)或三維球體對應區域(xi,yi,zi)的參考模型的溫度值和反演出的溫度值；TMm為參考模型的溫度算術平均值。

此外，基于超聲波換能器的溫度反演系統在實際應用過程中受到模數轉換精度、時間同步誤差和電磁擾動等噪聲的影響，為進一步模擬真實情況，本文在計算超聲波飛行時間時引入均值為0，標準差分別為0.02%、0.03%和0.05%的3種高斯白噪聲。

4.1 二維圓形平面的仿真驗證

首先構建區域半徑為2 m的圓形平面作為待測區域，同時在待測區域中對對角偏斜和中心對稱兩種溫度場模型開展數值模擬仿真，用于驗證本文所提方法的性能。

構建的對角偏斜溫度場模型為

(10)

構建的中心對稱的溫度場模型為

(11)

基于Matlab數值仿真平臺對對角偏斜和中心對稱兩類溫度場模型進行正演和反演。對角偏斜溫度場模型、中心對稱溫度場模型的仿真結果分別如圖4、5所示。由圖可以看出，引入白噪聲后，溫度場分布均能基本反應原溫度場模型，其中引入標準差為0.02%高斯白噪聲的反演結果與原模型最接近，而0.05%高斯白噪聲對應的結果較差。同時，定量分析的情況如表1所示，定量分析結果與定性分析結果一致。因此，采用基于徑向基函數的超聲波溫度場反演方法在二維圓形平面中的反演效果較好。

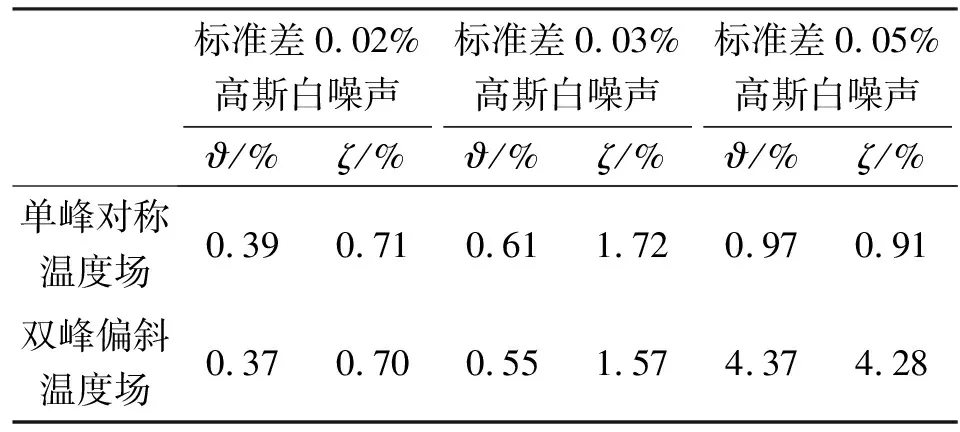
表1 二維圓形平面的反演誤差分析

4.2 三維球體平面的仿真驗證

首先構建區域半徑為4 m的球體平面作為待測區域，同時構建了中心對稱三維溫度場模型用于驗證，即：

(12)

基于Matlab數值仿真平臺對中心對稱三維溫度場模型進行正演和反演，仿真結果如圖6所示。由圖可以看出，引入白噪聲后的溫度場分布均能基本反應原溫度場模型，其中引入標準差為0.02%高斯白噪聲的反演結果與原模型最接近，而0.05%高斯白噪聲對應的結果較差。

定量分析的情況如表2所示，定量分析結果與定性分析結果一致。因此，采用基于徑向基函數的超聲波溫度場反演方法在三維球體的空間中的反演效果較好。

表2 三維球體空間的反演誤差分析

5 結束語

面向智能制造、智能汽車等領域對于非接觸式溫度場檢測的需求背景，本文基于收發一體式的超聲波信號飛行時間檢測原理設計了二維圓面和三維球體的多超聲波換能器空間拓撲結構，提出了采用分時輪訓的信號處理控制策略，并建立基于徑向基函數的溫度場反演算法實現了對二維、三維空間的溫度場重建。通過構建對角偏斜和中心對稱兩類溫度場模型對溫度場重建方案進行了仿真驗證，還通過引入高斯白噪聲對飛行時間的測量進行人工擾動，驗證了超聲測溫方法的魯棒性。