基于圖形設計的吸波材料表面波衰減特性研究

朱亞光,張 珊,王 蕾,蔡長旭,陸海鵬

(電子科技大學 國家電磁輻射控制材料工程技術研究中心,四川 成都 611731)

隨著隱身技術的發展,通過外形隱身和材料隱身已經能夠有效地控制現代飛行器等武器裝備的鏡面散射,而邊緣、縫隙、材料突變等因素導致的非鏡面散射就變得不可忽視,其中表面波散射是非鏡面散射中的重要組成部分,抑制表面波是進一步降低RCS 的有效手段。19 世紀90 年代,德國物理學家Sommerfeld[1]最先發現表面電磁波的存在,自此開啟了表面波研究的熱潮。

隨著對表面波的探索,很多關于表面波的研究集中在對其激勵和傳輸特性的分析上,Ling[2]、Ufimtsev[3-4]和趙伯琳[5-6]等對表面波的基本特性進行了分析,包括傳播常數、衰減、相位等,還推導了表面波衰減的經典色散方程。黃毅[7]通過改變吸收劑的填充比、球磨時間等觀察衰減常數變化規律。盡管對表面波的研究已經開展了一百多年,但關于改變表面波的衰減性能研究較少。陳海燕等[8]在經典色散方程的基礎上推導了有條件限制的表面波雙層色散方程,隨后通過加載電阻膜[9]和磁性薄膜[10]來改善表面波衰減性能。對于加載周期型結構的衰減性能研究更鮮有報道,黃大慶等[11]使用頻率選擇表面與吸波涂層結合,研究了不同頻率點的表面波衰減性能變化,但使用RCS 變化判斷表面波衰減的方法每次只能計算單個頻點。因此需要計算全頻段表面波衰減值的方法,對加載周期結構的寬頻帶表面波衰減性能進一步研究。

本文依據色散方程理論,利用磁性吸波材料分析了材料電磁參數對表面波衰減性能的影響,并設計圖案化結構與吸波材料相結合,使用反演法得到等效參數計算全頻段表面波衰減的變化,通過優化設計進一步改善衰減性能,為雷達吸波結構材料實現寬頻帶高表面波衰減提供了設計思路。

1 表面波的衰減計算

1.1 單層介質表面波衰減計算

基于Ufimtsev 等[2]對表面波的特性開展的一系列研究工作,其中表面波衰減的計算通過建立平面模型分析得到表面波的經典色散方程:

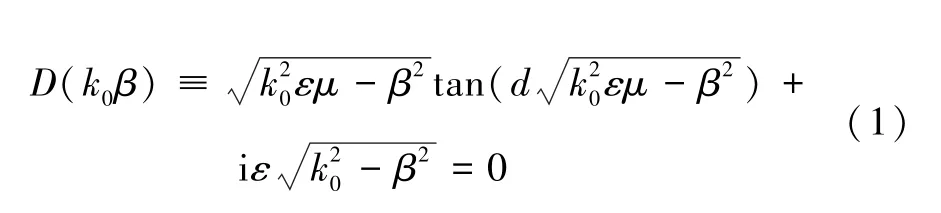
式中:k0是自由空間的波數;ε和μ分別是吸波材料的介電常數和磁導率;d為材料厚度。利用色散方程,在已知材料的電磁參數、厚度的情況下可計算得到表面波衰減值。

1.2 圖形單元結構表面波衰減計算

由于不能通過仿真計算圖案化結構的表面波衰減常數,因此采取將周期型結構等效為均勻介質,首先使用CST 仿真得到周期結構的S11和S21參數,進而使用反演法[12]代入公式可求得波阻抗Z和折射系數n:

得到最終的等效介電常數和磁導率為:

最后將計算出的等效電磁參數帶入色散方程進行計算,即可得出此結構的表面波衰減。

2 單層吸波材料的表面波衰減性能分析

根據表面波衰減計算公式,研究了單層吸波介質的厚度和電磁參數對表面波衰減性能的影響。所設頻率范圍為0～12 GHz,計算得到衰減常數的結果如圖1～2,可以看出衰減隨著頻率增加先達到最大值,然后逐漸降低達到零點,最后變為負值。負數形式的表面波衰減系數意味著在這些頻率點,表面波無論以何種角度入射均不可能被激勵產生,衰減達到零點的頻率稱為上限截止頻率[2]。

2.1 厚度對表面波衰減的影響

本文計算討論了厚度分別為1.5,2,2.5,3 mm吸波材料的衰減性能,如圖1 所示,可以看出隨著厚度的增加,同一頻段的衰減性能并不是隨之增強的,其衰減峰向低頻移動同時峰值不斷增大,但最大截止頻率不斷減小,衰減帶寬不斷變窄。綜合折中考慮,使用厚度為2 mm 的吸波材料進行后續的研究分析。

圖1 不同厚度吸波材料的衰減對比Fig.1 Attenuation comparison of absorbing materials with different thicknesses

2.2 電磁參數對表面波衰減的影響

接下來通過改變四個電磁參數中一個參數來對比分析該參數變化對衰減的影響,該參數變化比例為0.5 倍,1 倍,1.5 倍,2 倍,利用色散方程計算的結果如圖2。由圖2(a)可以看出隨著單層吸波材料介電常數實部的減小,衰減峰向高頻移動,衰減峰值不斷增大,上限截止頻率變大;圖2(b)中介電常數虛部對衰減影響不明顯,衰減峰值只會隨其增大略微減小;但磁導率實部對衰減影響顯著,隨著實部的增大衰減峰值不斷增大,上限截止頻率增大,如圖2(c)所示;由圖2(d)可知隨著磁導率虛部的增大,衰減峰向低頻移動且截止頻率減小,上限截止頻率減小。

圖2 材料的電磁參數變化對衰減的影響。(a) 改變介電常數實部;(b) 改變介電常數虛部;(c) 改變磁導率實部;(d) 改變磁導率虛部Fig.2 Effects of changes in electromagnetic parameters of the material on attenuation.(a) Change real part of permittivity;(b) Change imaginary part of permittivity;(c) Change real part of permeability;(d)Change imaginary part of permeability

因此可以得出結論:厚度會影響表面波衰減性能,低頻衰減性能會隨厚度的增大有所改善。介電常數實部會影響衰減峰值和上限截止頻率,虛部影響不大;磁導率實部增大對衰減峰值和截止頻率都有明顯改善,虛部會影響其上限截止頻率。

3 吸波結構的表面波衰減性能分析

上文研究了單層吸波材料的衰減特性,其材料參數會對其衰減性能產生一定影響,接下來在該材料的基礎上通過結構化設計觀察其衰減性能變化。

3.1 蛇形圖案吸波結構的設計及衰減性能分析

蛇形圖案吸波結構的基本單元如圖3 所示,其由三層結構構成,分別是底層金屬底板、中間磁性介質層以及最上層金屬方環圖案。其中金屬底板和金屬圖案均使用電導率為5.8×108S/m 的銅,頂層圖形單元是一個類似蛇形圈的金屬圖案。通過不斷調節確定最終的結構參數,結構單元周期為p=6 mm,豎條長度為l=0.8 mm,依次減小r=0.1 mm,橫條長度為y=0.3 mm,豎條和橫條寬度w=0.1 mm,介質層厚度為h=2 mm,金屬厚度為t=0.017 mm。

圖3 結構示意圖Fig.3 Schematic diagram of the unit cell

討論加載結構對衰減的影響,使用等效參數計算了該結構的表面波衰減。由圖4 可見加載結構后表面波衰減出現了兩個峰,同時高頻峰向高頻移動,上限截止頻率增大,從4 GHz 提高到8 GHz,但峰值減弱。

圖4 材料與結構的衰減對比Fig.4 Attenuation comparison of the material and the structure

3.2 改進型蛇形圖案吸波結構的設計及衰減性能分析

在蛇形圖案吸波結構的基礎上,將中間磁性介質層由完整的磁性單元材料變為挖去中間方環部分,挖空至金屬底板,形成改進型蛇形圖案吸波結構,形成過程如圖5。挖去的方環結構外環長度a=2.7 mm,內環長度b=1.9 mm。改進型結構示意圖如圖6。

圖5 結構的形成過程Fig.5 Schematic diagram of the structure formation process

圖6 改進型結構示意圖Fig.6 Schematic diagram of the optimized unit cell

分析此種結構的衰減變化,由圖7 可見,與蛇形圖案吸波結構相比,改進型蛇形圖案吸波結構的高頻峰向高頻移動,同時峰值增大,上限截止頻率進一步增大,使上限截止頻率從6 GHz 提高到8 GHz。改變結構周期,將等效參數帶入色散方程可得p在6～15 mm 范圍內變化的表面波衰減常數,從圖8 中可見隨著結構周期的增大,衰減峰向低頻移動,上限截止頻率減小,同時峰值呈現先增大后減小的趨勢。因此可以得出結論:利用結構化設計可使衰減性能產生一定改變,通過合理設計可進一步改善表面波衰減性能,有望利用此方式實現寬頻范圍的高衰減性能。

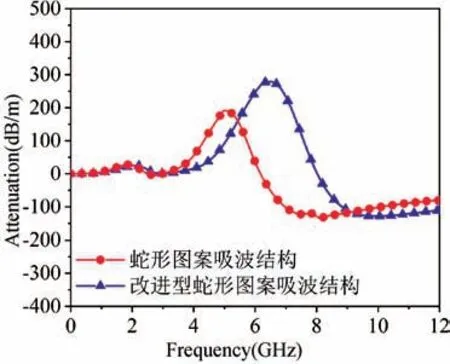
圖7 兩種結構的衰減對比Fig.7 Attenuation comparison of two structures

圖8 吸波材料不同周期的衰減對比Fig.8 Attenuation comparison of absorbing materials with different patterns

4 結論

本文通過分析不同厚度和不同電磁參數的吸波材料表面波衰減性能,發現并不是材料厚度越大衰減性能越好,四個電磁參數對表面波衰減都有一定影響;將圖案化結構與吸波材料相結合可在不改變厚度的情況下改變表面波衰減性能。本文設計了一種蛇形圖案吸波結構,使衰減上限截止頻率從4 GHz 拓寬到6 GHz,但峰值減弱。對結構進行優化,將中間磁性介質層挖孔,設計出一種改進型蛇形圖案吸波結構,將衰減上限截止頻率進一步拓寬到8 GHz,衰減峰值也得到了提高。因此應根據實際需要選擇合適的參數,并可通過合理設計結構改善衰減性能,進一步增強表面波衰減性能,從而實現寬頻帶范圍的高衰減性能。