?ayl所構造二元算子成一致模的一些條件
王學平 ,何 鵬
(1.四川師范大學 數學科學學院, 四川 成都 610066;2.成都信息工程大學 應用數學學院, 四川 成都 610225)
三角模和三角余模最初是由Schweizer和Sklar介紹的[1]。 為推廣三角模和三角余模, Yager和Rybalov定義并研究了[0,1]上一致模。 一致模在模糊邏輯、模糊系統模擬、專家系統及神經網絡等許多領域中都扮演著重要角色[2-4]。 因為[0,1]是有界格的特例, 所以學者們自然地想嘗試在有界格上構造和討論一致模[5-15]。例如,Kara?al和Mesiar率先討論了有界格上一致模[16],證明了任意包含最大元1和最小元0的有界格L上存在一致模, 并構造了有界格上最大一致模和最小一致模。 此后, 國內外許多學者研究了有界格L上以e∈L{ 0,1}為單位元的一致模的構造方法。 現有文獻中有界格上一致模的構造方法主要分為兩大類, 一類是用子區間[0,e]上三角模或子區間[e, 1]上三角余模構造有界格L上的一致模。 比如, ?ayl、 Kara?al和Mesiar分別用三角模和三角余模給出了有界格上一致模的兩個構造方法, 由此得到了有界格上的最大和最小冪等一致模[11]。 此外, 他們還證明了任意非鏈有界格上存在既不是合取的(conjunctive)又不是析取的(disjunctive)冪等一致模。 之后,?ayl分別用子區間上的三角模和三角余模又給出了兩種新的構造一致模的方法[6], 并舉例說明其構造法與已有構造法不同。 Ouyang和Zhang結合三角模或三角余模利用閉包算子和內部算子構造了有界格上一致模[17], 推廣了文獻[11,16]中一些對應結論。 最近, Ac和Mesiar也通過三角模和三角余模分別給出了兩個構造有界格上一致模的方法, 并根據該方法得到有界格上冪等一致模[5]。
有界格上一致模的另一類構造方法是同時用子區間[0,e]上三角模和[e,1]上三角余模構造一致模。比如, ?ayl用三角模和三角余模給出了兩個構造有界格上一致模的方法[8], 不過, 其中的三角模和三角余模需滿足嚴格的邊界條件。 同年, Dan等在單位元滿足某些限制條件下用三角模和三角余模給出了兩個構造有界格上一致模的新方法[13]。 之后, Xie和Li給出了兩個基于三角模和三角余模構造有界格上一致模的方法[18], 證明了如果對三角模Te和三角余模Se加上同樣的限制, 則他們構造的一致模分別是最大的和最小的。 而且, 在他們的構造中不需要三角模和三角余模滿足邊界條件, 因此, 完全回答了?ayl在文獻[8]中提出的開問題。 最近, Zhao和Wu在給定三角模與三角余模的基礎上利用閉包算子和內部算子給出了三個構造有界格上一致模的方法[19], 他們的結論也回答了?ayl在文獻[8]中提出的開問題。 特別地, Ji用比三角模和三角余模更一般的子三角模和子三角余模構造了有界格上一些一致模[20], 推廣了文獻[11-12,16]中一些已有構造。
有界格上現有以e∈L{0,1}為單位元的一致模U的構造方法都有一個共同特征, 即, 當(x,y)∈(0,e)×Ie時U(x,y)∈Ie, 或(x,y)∈(e,1) ×Ie時U(x,y)∈Ie, 其中Ie是由L中所有與e不可比的元構成的集合。 而在文獻[9]中, ?ayl利用[0,e]上的三角模Te和[e,1]上的三角余模Se構造的一致模U在(x,y)∈(0,e)×Ie∪ (e,1)×Ie時,U(x,y)?Ie。設A(e)= [0,e)×(e,1]∪(e,1]×[0,e),則?ayl的構造具體如下。
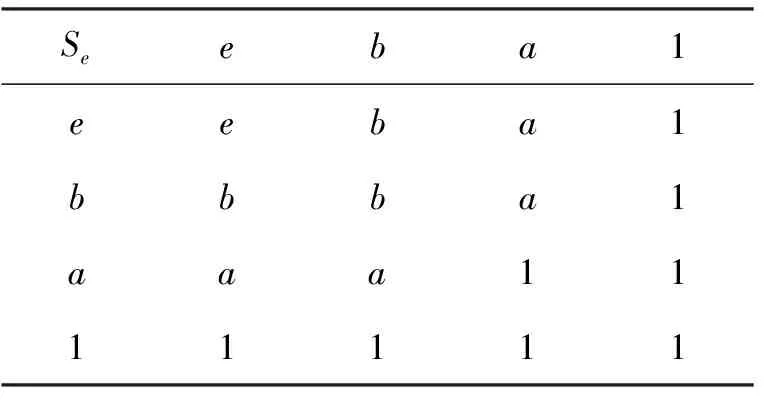
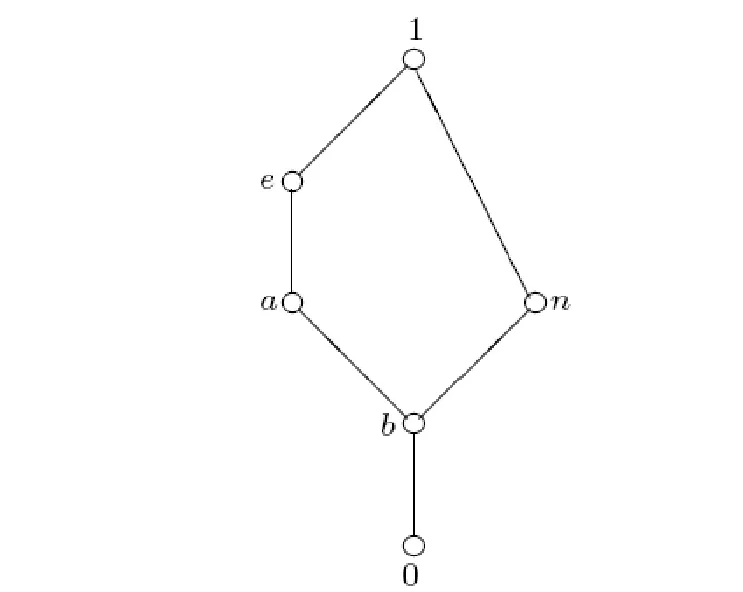
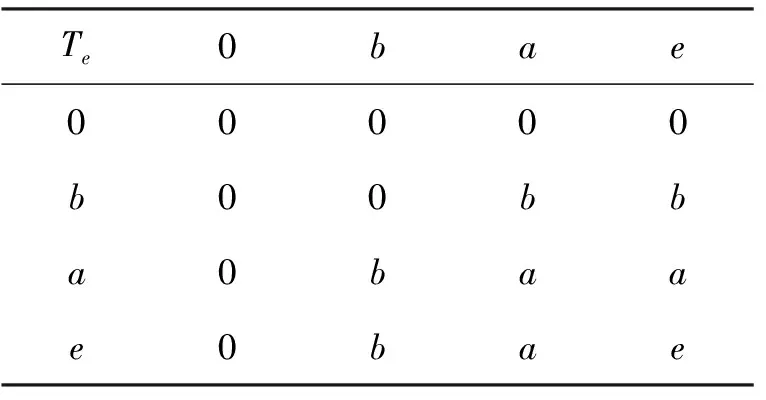
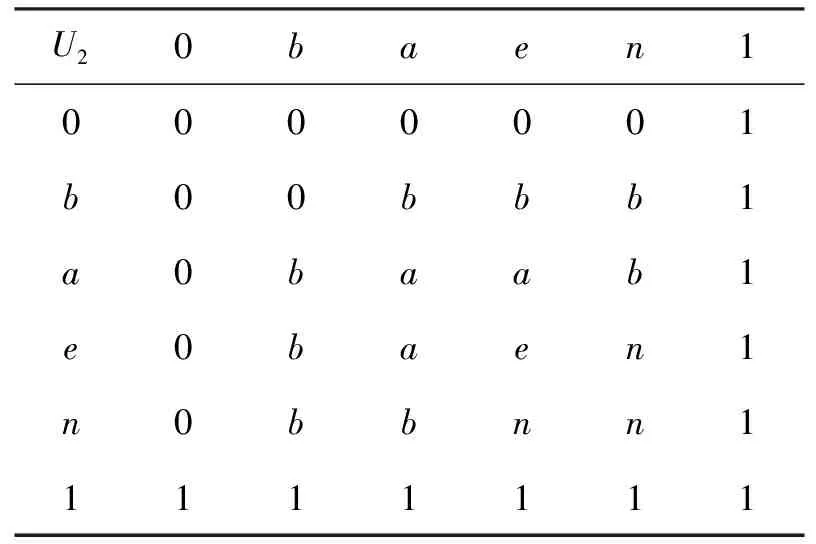
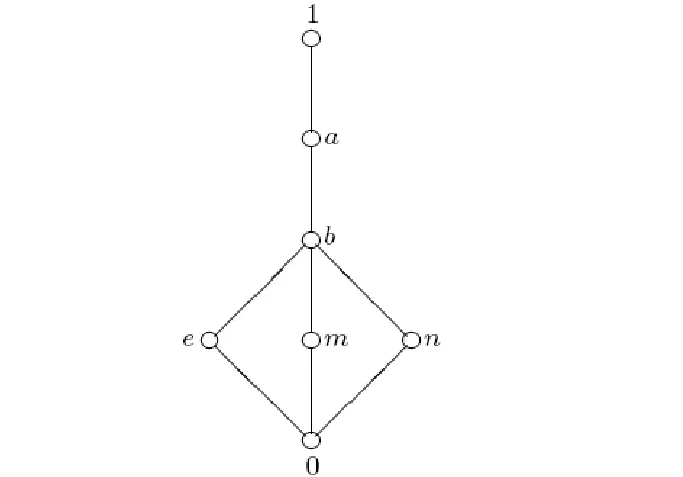
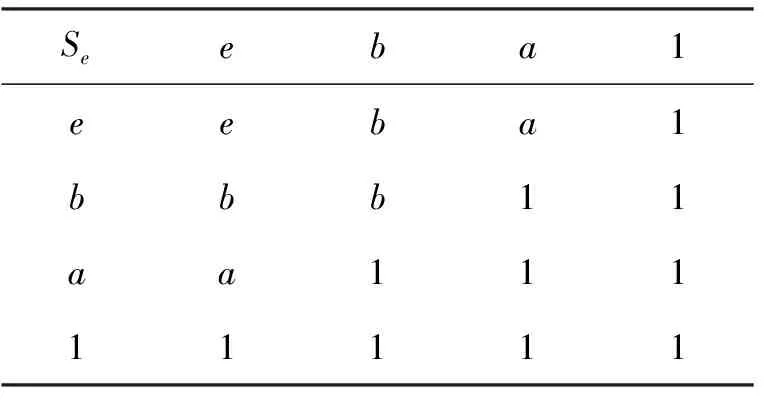
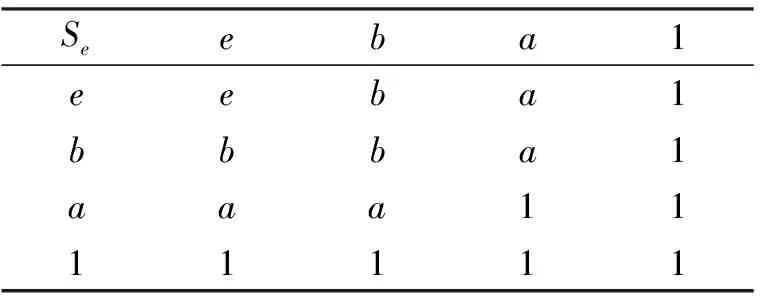
定理1(文獻[9]中定理7 ) 設e∈L{0,1}使對任意x∈Ie,y∈(e,1]有x U1(x,y) = (1) 定義的二元算子U1:L2→L是L上以e為單位元的一致模當且僅當對任意x∈Ie,y∈[0,e)有x>y。 定理2(文獻[9]中定理10) 設e∈L{0,1},使對任意x∈Ie,y∈[0,e)有x>y, 且對任意p,q∈Ie有p∧q∈Ie。若Te是[0,e]上的三角模,Se是[e,1]上的三角余模, 則對任意x,y∈L, 由 U2(x,y) = (2) 定義的二元算子U2:L2→L是L上以e為單位元的一致模,當且僅當對任意x∈Ie,y∈(e,1]有x 關于上面兩個定理, 有兩點值得注意:①定理1中, 條件“對任意p,q∈Ie有p∨q∈Ie”是充分但不必要的。 即, 對[e,1]上的很多三角余模Se,該條件可以去掉, 例如取Se=S∨。②定理2中, 條件“對任意p,q∈Ie有p∧q∈Ie”是充分但不必要的。 即,對[0,e]上的很多三角模Te, 該條件可以去掉, 例如取Te=T∧。 問題是: 在什么條件下, 由式(1)和式(2)所定義的二元算子U1,U2分別是有界格L上的一致模? 本文將圍繞該問題展開討論并給出回答。 為便于討論, 本節回顧一些關于格、三角模、三角余模和一致模的基本概念和結論, 更多相關內容請參見文獻[6,8,11,16,18,21-23]。 設P為非空集合, 若≤是P上滿足自反性、反對稱性和傳遞性的二元關系, 則稱(P,≤)為偏序集。若偏序集(L,≤)中任意兩個元{x,y}在L中有最大下界x∧y(也稱為下確界)和最小上界x∨y(也稱為上確界),則稱(L,≤)為格。若格(L,≤)有最大元1和最小元0, 則稱該格為有界格, 記為(L,≤,0,1)。本文以下用L代替(L,≤,0,1)。設a,b∈L且a≤b,定義L的閉子區間[a,b]如下:[a,b]={x∈L:a≤x≤b}。可以類似地定義L的其他子區間:[a,b) = {x∈L:a≤x {x∈L:a 定義1[21-22]1) 若有界格L上對每個變量單調不減有單位元1的二元算子T:L2→L滿足交換律與結合律, 則稱T為L上三角模。 2) 若有界格L上對每個變量單調不減有單位元0的二元算子S:L2→L滿足交換律與結合律, 則稱S為L上三角余模。 下面是有界格L上常見的兩對三角模和三角余模: T∧(x,y)=x∧y, S∨(x,y)=x∨y, 特別地, 若L=[0,1],則T∧=TM;TW=TD;S∨=SM且SW=SD。 定義2[16]若有界格L上對每個變量單調不減有單位元e的二元算子U:L2→L滿足交換律與結合律,則稱U為L上一致模。 顯然, 有界格上L的三角模和三角余模分別是L上的一致模。 定義3[11,18]設U是有界格L上以e∈{0,1}為單位元的一致模。若對任意x∈L有U(x,x)=x,則稱U是冪等的。 性質1[16]設U是有界格L上以e∈{0,1}為單位元的一致模, 則 1)Te=U|[0,e]2: [0;e]2→[0,e]是[0,e]上的三角模; 2)Se=U|[e,1]2: [e; 1]2→[e,1]是[e,1]上的三角余模。 性質2[16]設U是有界格L上以e∈{0,1}為單位元的一致模, 則 1) 對任意的(x,y)∈A(e), 有x∧y≤U(x,y)≤x∨y; 2) 對任意的(x,y)∈L×[0,e], 有U(x,y)≤x; 3) 對任意的(x,y)∈[0,e]×L, 有U(x,y)≤y; 4) 對任意的(x,y)∈L×[e,1], 有x≤U(x,y); 5) 對任意的(x,y)∈[e,1]×L, 有y≤U(x,y)。 以下設L是有界格且a,b∈L, 記號a‖b表示ab且ab, 而ab表示a≥b或a≤b,Ia={x∈L:x‖a}。 引理1設e∈L{0, 1},使對任意x∈Ie,y∈(e,1]有x 引理2設e∈L{0, 1}使對任意x∈Ie,y∈(e,1]有x 證明設U1是L上以e為單位元的一致模且存在p,q∈Ie使p∨q?Ie, 則根據文獻[9]中定理7的證明易知,若x∈Ie,y∈[0,e), 則x>y。另一方面, 由引理1知∧t ∈(e,1]t=p∨q∈(e,1]。所以, 若存在元z∈(e,1]使Se(∧t ∈(e,1]t,z)≠z, 則U1(p,U1(q,z))=U1(p,z)=z≠Se(∧t ∈(e,1]t,z)=U1(p∨q,z)=U1(U1(p,q),z)。因此,U1不滿足結合律, 與U1是L上的一致模相矛盾。 反之, 由式(1)易知二元算子U1滿足交換律且e是它的單位元。下面證明U1滿足結合律且對每個變量單調不減。由U1是交換的知, 要證U1對每個變量單調不減, 僅需證對任意x,y,z∈L,x≤y蘊含U1(x,z)≤U1(y,z)。又由于z=e時,U1(x,z)=U1(x,e)=x≤y=U1(y,e)=U1(y,z),所以分以下4種情況驗證x≤y蘊含U1(x,z)≤U1(y,z): 情況1 若x∈[0,e), 1.1y∈[0,e), 1.1.1z∈[0,e), U1(x,z)=Te(x,z)≤Te(y,z)=U1(y,z)。 1.1.2z∈(e,1], U1(x,z)=x∧z≤y∧z=U1(y,z)。 1.1.3z∈Ie, U1(x,z)=x∧z≤y∧z=U1(y,z)。 1.2y∈(e,1], 1.2.1z∈[0,e), U1(x,z)=Te(x,z)≤x∧z≤y∧z=U1(y,z)。 1.2.2z∈(e,1], U1(x,z)=x∧z≤y∨z≤Se(y,z)=U1(y,z)。 1.2.3z∈Ie, U1(x,z)=x∧z≤y∨z=U1(y,z)。 1.3y∈Ie, 1.3.1z∈[0,e), U1(x,z)=Te(x,z)≤x∧z≤y∧z=U1(y,z)。 1.3.2z∈(e,1], U1(x,z)=x∧z≤y∨z=U1(y,z)。 1.3.3z∈Ie, U1(x,z)=x∧z≤y∨z=U1(y,z)。 1.4y=e, 1.4.1z∈[0,e), U1(x,z)=Te(x,z)≤z=U1(e,z)=U1(y,z)。 1.4.2z∈(e,1], U1(x,z)=x∧z≤z=U1(e,z)=U1(y,z)。 1.4.3z∈Ie, U1(x,z)=x∧z≤z=U1(e,z)=U1(y,z)。 情況2 若x∈(e,1],則y∈(e,1]。 2.1z∈[0,e), U1(x,z)=x∧z≤y∧z=U1(y,z)。 2.2z∈(e,1], U1(x,z)=Se(x,z)≤Se(y,z)=U1(y,z)。 2.3z∈Ie, U1(x,z)=x∨z≤y∨z=U1(y,z)。 情況3 若x∈Ie, 則y?[0,e]。否則,x≤y≤e, 與x∈Ie相矛盾。 3.1y∈(e,1], 3.1.1z∈[0,e), U1(x,z)=x∧z≤y∧z=U1(y,z)。 3.1.2z∈(e,1], U1(x,z)=x∨z≤y∨z≤Se(y,z)=U1(y,z)。 3.1.3z∈Ie, U1(x,z)=x∨z≤y∨z=U1(y,z)。 3.2y∈Ie, 3.2.1z∈[0,e), U1(x,z)=x∧z≤y∧z=U1(y,z)。 3.2.2z∈(e,1], U1(x,z)=x∨z≤y∨z=U1(y,z)。 3.2.3z∈Ie, U1(x,z)=x∨z≤y∨z=U1(y,z)。 情況4 若x=e, 則y∈[e,1]。 4.1y=e, U1(x,z)=U1(e,z)=U1(y,z)。 4.2y∈(e,1], 4.2.1z∈[0,e), U1(x,z)=U1(e,z)=z=y∧z=U1(y,z)。 4.2.2z∈(e,1], U1(x,z)=U1(e,z)=z≤Se(y,z)=U1(y,z)。 4.2.3z∈Ie, U1(x,z)=U1(e,z)=z≤y∨z=U1(y,z)。 下證U1滿足結合律, 即, 需證明對任意x,y,z∈L有U1(U1(x,y),z)=U1(x,U1(y,z))。由于e∈{x,y,z}時,U1(U1(x,y),z)=U1(x,U1(y,z)),所以以下討論不考慮e∈{x,y,z}的情況。由引理1知, 若p,q∈Ie且p∨q?Ie, 則 (3) 以下分3種情況驗證U1滿足結合律: 情況1 若x∈[0,e), 1.1y∈[0,e), 1.1.1z∈[0,e), U1(U1(x,y),z)=Te(Te(x,y),z)= Te(x,Te(y,z))=U1(x,U1(y,z))。 1.1.2z∈(e,1], U1(U1(x,y),z)=U1(Te(x,y),z)= Te(x,y)=U1(x,y)=U1(x,U1(y,z))。 1.1.3z∈Ie, U1(U1(x,y),z)=U1(Te(x,y),z)= Te(x,y)=U1(x,y)=U1(x,U1(y,z))。 1.2y∈(e,1], 1.2.1z∈[0,e), U1(U1(x,y),z)=U1(x,z)=Te(x,z)= U1(x,U1(y,z))。 1.2.2z∈(e,1], U1(U1(x,y),z)=U1(x,z)=x= U1(x,Se(y,z))=U1(x,U1(y,z))。 1.2.3z∈Ie, U1(U1(x,y),z)=U1(x,z)=x= U1(x,y∨z)=U1(x,U1(y,z))。 1.3y∈Ie, 1.3.1z∈[0,e), U1(U1(x,y),z)=U1(x,z)=Te(x,z)= U1(x,U1(y,z))。 1.3.2z∈(e,1], U1(U1(x,y),z)=U1(x,z)=x= U1(x,y∨z)=U1(x,U1(y,z))。 1.3.3z∈Ie, 無論y∨z∈Ie還是y∨z∈(e,1], 均有 U1(U1(x,y),z)=U1(x,z)=x=U1(x,y∨z)=U1(x,U1(y,z))。 情況2 若x∈(e,1], 2.1y∈[0,e), 2.1.1z∈[0,e), U1(U1(x,y),z)=U1(y,z)=Te(y,z)= U1(x,Te(y,z))=U1(x,U1(y,z))。 2.1.2z∈(e,1], U1(U1(x,y),z)=U1(y,z)=y= U1(x,y)=U1(x,U1(y,z))。 2.1.3z∈Ie, U1(U1(x,y),z)=U1(y,z)=y= U1(x,y)=U1(x,U1(y,z))。 2.2y∈(e,1], 2.2.1z∈[0,e), U1(U1(x,y),z)=U1(Se(x,y),z)=z= U1(x,z)=U1(x,U1(y,z))。 2.2.2z∈(e,1], U1(U1(x,y),z)=Se(Se(x,y),z)= Se(x,Se(y,z))=U1(x,U1(y,z))。 2.2.3z∈Ie, U1(U1(x,y),z)=U1(Se(x,y),z)= Se(x,y)=U1(x,y)=U1(x,U1(y,z))。 2.3y∈Ie, 2.3.1z∈[0,e), U1(U1(x,y),z)=U1(x∨y,z)=z= U1(x,z)=U1(x,U1(y,z))。 2.3.2z∈(e,1], U1(U1(x,y),z)=U1(x,z)=Se(x,z)= U1(x,U1(y,z))。 2.3.3z∈Ie, 由式(3)有y∨z=∧t∈(e,1]t,或者y∨z∈Ie。 2.3.3.1y∨z=∧t∈(e,1]t, U1(U1(x,y),z)=U1(x,z)=x= Se(x,y∨z)=U1(x,U1(y,z))。 2.3.3.2y∨z∈Ie, U1(U1(x,y),z)=U1(x,z)=x= U1(x,y∨z)=U1(x,U1(y,z))。 情況3 若x∈Ie, 3.1y∈[0,e), 3.1.1z∈[0,e), U1(U1(x,y),z)=U1(y,z)=Te(y,z)= U1(x,Te(y,z))=U1(x;U1(y,z))。 3.1.2z∈(e,1], U1(U1(x,y),z)=U1(y,z)=y= U1(x,y)=U1(x,U1(y,z))。 3.1.3z∈Ie, U1(U1(x,y),z)=U1(y,z)=y= U1(x,y)=U1(x,U1(y,z))。 3.2y∈(e,1], 3.2.1z∈[0,e), U1(U1(x,y),z)=U1(x∨y,z)=z= U1(x,z)=U1(x,U1(y,z))。 3.2.2z∈(e,1], U1(U1(x,y),z)=U1(y,z)=Se(y,z)= U1(y,z)=U1(x,U1(y,z))。 3.2.3z∈Ie, U1(U1(x,y),z)=U1(y,z)=y= U1(x,y)=U1(x,U1(y,z))。 3.3y∈Ie, 3.3.1z∈[0,e), 無論x∨y∈Ie,還是x∨y∈(e,1],均有 U1(U1(x,y),z)=U1(x∨y,z)=z=U1(x,z)=U1(x,U1(y,z))。 3.3.2z∈(e,1], 由式(3)知x∨y=∧t∈(e,1]t,或者x∨y∈Ie。 3.3.2.1x∨y=∧t∈(e,1]t, U1(U1(x,y),z)=Se(x∨y,z)=z= U1(x,z)=U1(x,U1(y,z))。 3.3.2.2x∨y∈Ie, U1(U1(x,y),z)=U1(x∨y,z)=z= U1(x,z)=U1(x,U1(y,z))。 3.3.3z∈Ie, 無論x∨y∈Ie,還是x∨y∈(e,1],均有U1(U1(x,y),z)=U1(x∨y,z)=x∨y∨z。 可類似證明U1(x,U1(y,z))=U1(x,y∨z)=x∨y∨z。 因此,U1(U1(x,y),z)=x∨y∨z=U1(x,U1(y,z))。 綜上,U1是L上以e為單位元的一致模。 注1引理2中條件“對任意x∈Ie,y∈(e,1]有x a)x∈Ie,y∈Ie,z∈(e,1]; b)x∈(e,1],y∈Ie,z∈Ie; c)x∈Ie,y∈(e,1],z∈(e,1]; d)x∈(e,1],y∈(e,1],z∈Ie; e)x∈(e,1],y∈Ie,z∈(e,1]。 例1設L1是圖1所示的有界格, 易見對任意x∈Ie,y∈[0,e)有x>y。n∈Ie,b∈(e,1]且b‖n。又設Se是表1所定義的[e,1]上滿足對任意z∈(e,1]有Se(∧t∈(e,1]t,z)=Se(b,z)=z的三角余模,Te=T∧是[0,e]的三角模。 圖1 有界格L1Fig.1 A bounded lattice L1 由式(1)易知L1上二元算子U1如表2所示, 因此 U1(U1(m,n),a)=U1(a,a)=1,但U1(m,U1(n,a))=U1(m,a)=a; U1(U1(a,m),n)=U1(a,n)=a,但U1(a,U1(m,n))=U1(a,a)=1; U1(U1(n,r),k)=U1(a,k)=1,但U1(n,U1(r,k))=U1(n,k)=a; U1(U1(r,k),n)=U1(k,n)=a,但U1(r,U1(k,n))=U1(r,a)=1; U1(U1(b,n),k)=U1(a,k)=1,但U1(b,U1(n,k))=U1(b,a)=a。 因此,U1不滿足結合律。從而U1不是一致模。 表1 [e,1]上的三角余模SeTab.1 The t-conorm Seon [e,1] 表2 L1上的二元算子U1Tab.2 The binary operator U1on L1 注2引理2中條件“對任意z∈(e,1]有Se(∧t ∈(e,1]t,z)=z”是U1在以下情況滿足結合律的充要條件: i)x∈Ie,y∈Ie,z∈(e,1]且x∨y?Ie; ii)x∈(e,1],y∈Ie,z∈Ie且y∨z?Ie。 首先看情況i), 假設條件“對任意z∈(e,1],有Se(∧t ∈(e,1]t,z)=z”不是必要的, 即, 當Se(∧t ∈(e,1]t,z)≠z且i)成立時,U1滿足結合律。由引理1得∧t ∈(e,1]t=x∨y,因此,U1(U1(x,y),z)=U1(x∨y,z)=Se(x∨y,z)≠z=U1(x,z)=U1(x,U1(y,z)), 矛盾。類似可證條件“對任意z∈(e,1]有Se(∧t ∈(e,1]t,z)=z”也是U1在情況ii)滿足結合律的必要條件。 下例說明條件“對任意z∈(e,1]有Se(∧t ∈(e,1]t,z)=z”是U1分別在情況i)和ii)滿足結合律的充分條件。 例2設L2為圖2所示有界格, 易見對任意x∈Ie,y∈[0,e)有x>y,對任意x∈Ie,y∈(e,1]有x 圖2 有界格L2Fig.2 A bounded lattice L2 表3 [e,1]上的三角余模SeTab.3 The t-conorm Seon [e,1] 表4 L2上的二元算子U1Tab.4 The binary operator U1on L2 由式(1)易知L2上二元算子U1如表4所示, 因此 U1(U1(m,n),a)=U1(b,a)=1,但U1(m,U1(n,a))=U1(m,a)=a; U1(U1(a,m),n)=U1(a,n)=a,但U1(a,U1(m,n))=U1(a,b) = 1。 所以,U1不滿足結合律。從而U1不是一致模。 例3再次考慮圖2中有界格L2。設Te=T∧為[0,e]上三角模,Se為[e,1]上由表5定義的三角余模。 顯然, 對任意z∈(e,1],Se(∧t ∈(e,1]t,z)=Se(b,z)=z。則由引理2可得L2上一致模U1如表6所示。 表5 [e,1]上的三角余模SeTab.5 The t-conorm Seon [e,1] 表6 L2上的一致模U1Tab.6 The uninorm U1on L2 由定理1和引理2可知如下定理成立。 定理3設e∈L{0,1}使對任意x∈Ie,y∈(e,1]有x 1) 對任意x∈Ie,y∈[0,e)有x>y; 2) 對任意p,q∈Ie有p∨q∈Ie。否則, 對任意z∈(e,1]有Se(∧t ∈(e,1]t,z)=z。 由定理3可得下面推論。 推論1設e∈L{0,1}使對任意x∈Ie,y∈(e,1]有x 為解釋定理3中條件“對任意x∈Ie,y∈(e,1]有x 定理4(文獻[9]中定理6) 設Te是[0,e]上的三角模, 則對任意x,y∈L,由 U3(x,y)= 定義的二元算子U3:L2→L是L上以e為單位元的一致模當且僅當對任意x∈Ie,y∈[0,e)有x>y。 由注1和例1可知, 定理1中條件“對任意x∈Ie,y∈(e,1]有x 定理5設e∈L{0,1}使對任意x∈Ie,y∈(e,1]有x‖y,Te是[0,e]上的三角模,Se是[e,1]上的三角余模,則式(1)定義的二元算子U1是L上以e為單位元的一致模當且僅當對任意x∈Ie,y∈[0,e)有x>y。 證明若U1是L上以e為單位元的一致模, 則類似引理2的證明, 可證對任意x∈Ie,y∈[0,e)有x>y。 以下假設對任意x∈Ie,y∈[0,e)有x>y, 接下來證明U1是L上以e為單位元的一致模。類似于引理2的證明, 可證U1關于每個變量單調不減。又由式(1)易知U1滿足交換律且e是它的單位元。因此, 只需驗證U1滿足結合律。即, 證明對任意x,y,z∈L有U1(U1(x,y),z)=U1(x;U1(y,z))。根據引理2中結合律的證明,只需在如下6種情況驗證U1滿足結合律即可: 情況1 設x∈Ie,y∈Ie且z∈(e,1], 1.1 若x∨y=1, 則 U1(U1(x,y),z)=U1(x∨y,z)= U1(1,z)=Se(1,z)=1= x∨1=U1(x,1)= U1(x,y∨z)= U1(x,U1(y,z))。 1.2 若x∨y∈Ie, 則 U1(U1(x,y),z)=U1(x∨y,z)= x∨y∨z=1=x∨1= U1(x,1)=U1(x,y∨z)= U1(x,U1(y,z))。 情況2 設x∈Ie,y∈(e,1]且z∈Ie, 則 U1(U1(x,y),z)=U1(x∨y,z)= U1(1,z)=1∨z=1=x∨1= U1(x,1)=U1(x,y∨z)= U1(x,U1(y,z))。 情況3 設x∈(e,1],y∈Ie且z∈Ie, 則由情況1知 U1(U1(x,y),z)=U1(z,U1(x,y))= U1(z,U1(y,x))=U1(U1(z,y),x)= U1(x,U1(z,y))=U1(x,U1(y,z))。 情況4 設x∈Ie,y∈(e,1]且z∈(e,1], 則 U1(U1(x,y),z)=U1(x∨y,z)= U1(1,z)=Se(1,z)=1= x∨Se(y,z)=U1(x,Se(y,z))= U1(x,U1(y,z))。 情況5 設x∈(e,1],y∈Ie且z∈(e,1], 則 U1(U1(x,y),z)=U1(x∨y,z)= U1(1,z) =Se(1,z) = 1= Se(x,1)=Se(x,y∨z)= U1(x,y∨z)=U1(x,U1(y,z))。 情況6 設x∈(e,1],y∈(e,1]且z∈Ie, 則由情況4知 U1(U1(x,y),z)=U1(z,U1(x,y))= U1(z,U1(y,x))= U1(U1(z,y),x)= U1(x,U1(z,y))= U1(x,U1(y,z))。 綜上,U1是L上以e為單位元的一致模。 注3由例1可知, 定理5中條件“對任意x∈Ie,y∈(e,1)有x‖y”是U1為L上一致模的充分條件。若在定理5中取Se=S∨, 則二元算子U1等同于定理4中的U3。所以, 條件“對任意x∈Ie,y∈(e,1)有x‖y”不是U1為L上一致模的必要條件。 例4設L3為圖3所示的有界格, [0,e]上的三角模為Te=T∧, [e,1]上的三角余模為Se=SW, 則由定理5知表7所示的二元算子U1是L3上以e為單位元的一致模。 圖3 有界格L3Fig.3 A bounded lattice L3 表7 L3上的一致模U1Tab.7 The uninorm U1on L3 引理3設e∈L{0,1}使對任意x∈Ie,y∈[0,e)有x>y。若p,q∈Ie且p∧qIe, 則∨t ∈[0,e)t=p∧q。 證明類似于引理1的證明。 引理4設e∈L{0,1},使對任意x∈Ie,y∈[0,e)有x>y,Te是[0,e]上的三角模,Se是[e,1]上的三角余模。如果存在兩個元p,q∈Ie使p∧q?Ie, 則式(2)定義的二元算子U2是L上以e為單位元的一致模當且僅當對任意x∈Ie,y∈(e,1]有x 證明類似于引理2的證明。 類似于注1和注2, 有如下兩個結論成立。 注4引理4中, 條件“對任意x∈Ie,y∈[0,e)有x>y”是U2在如下情況滿足結合律的充分條件: 1)x∈Ie,y∈Ie,z∈[0,e); 2)x∈[0,e),y∈Ie,z∈Ie; 3)x∈Ie,y∈[0,e),z∈[0,e); 4)x∈[0,e),y∈[0,e),z∈Ie; 5)x∈[0,e),y∈Ie,z∈[0,e)。 注5引理4中, 條件“對任意z∈[0,e)有Te(∨t ∈[0,e)t,z)=z”是U2在如下情況滿足結合律的充要條件: 1)x∈Ie,y∈Ie,z∈[0,e)且x∧y?Ie; 2)x∈[0,e),y∈Ie,z∈Ie且y∧z?Ie。 由定理2和引理4易知下面定理成立。 定理6設e∈L{0,1}使對任意x∈Ie,y∈[0,e)有x>y,Te是[0,e]上的三角模,Se是[e,1]上的三角余模,則式(2)定義的二元算子U2是L上以e為單位元的一致模當且僅當如下兩個條件成立: 1) 對任意x∈Ie,y∈(e,1]有x 2) 對任意p,q∈Ie有p∧q∈Ie。否則, 對任意z∈[0,e)有Te(∨t ∈[0,e)t,z)=z。 由定理6知下面推論成立。 推論2設e∈L{0,1}使得對任意x∈Ie,y∈[0,e)有x>y,Se是[e,1]上的三角余模,Te是[0,e]上滿足對任意z∈[0,e)有Te(∨t ∈[0,e)t,z)=z的三角模, 則式(2)定義的二元算子U2是L上以e為單位元的一致模當且僅當對任意x∈Ie,y∈(e,1]有x 為解釋定理6中條件“對任意x∈Ie,y∈[0,e)有x>y”不是式(2)定義的U2為L上一致模的必要條件,需引入下面定理。 定理7(文獻[9]中定理9) 設Se是[e,1]上的三角余模, 則對任意x,y∈L, 由 U4(x,y)= 定義的二元算子U4:L2→L是L上以e為單位元的一致模當且僅當對任意x∈Ie,y∈(e,1]有x 根據注4和定理7, 定理6中條件“對任意x∈Ie,y∈[0,e)有x>y”是式(2)定義的U2為L上一致模的充分但不必要的條件。進一步, 有下面定理。 定理8設e∈L{0,1}使對任意x∈Ie,y∈(0,e)有x‖y,Te是[0,e]上的三角模,Se是[e,1]上的三角余模,則式(2)定義的二元算子U2是L上以e為單位元的一致模當且僅當對任意x∈Ie,y∈(e,1]有x 證明類似于定理5的證明。 類似于注3, 定理8中條件“對任意x∈Ie,y∈(e,1)有x‖y”是U2為L上一致模的充分但不必要的條件。 圖4 有界格L4Fig.4 A bounded lattice L4 表8 [e,1]上的三角余模SeTab.8 The t-conorm Seon [e,1] 表9 L4上的二元算子U1Tab.9 The binary operator U1on L4 易驗證, 對任意x∈Ie,y∈[0,e)有x>y, 對任意p,q∈Ie有p∨q∈Ie且對任意z∈(e,1]有Se(∧t∈(e,1]t,z)=z。然而由式(1)易見二元算子U1如表9所示。因為U1(U1(n,b),a)=U1(a,a)=1≠a=U1(n,a)=U1(n,U1(b,a)),所以U1不是一致模。 同時, 分別在對任意x∈Ie,y∈[0,e)有x>y和對任意x∈Ie,y∈(0,e)有x‖y兩種情況下, 給出了式(2)定義的二元算子U2是有界格L上一致模的兩個充要條件(見定理6和定理8)。因為對任意x∈Ie,y∈[0,e)有xy, 所以從完整性的角度, 自然要問, 如果存在兩個元(x,y),(u,v) ∈Ie×(0,e)使x>y且u‖v, 那么由式(2)定義的U2為L上一致模的充要條件是什么? 一般說來, 此時式(2)定義的U2不再是L上的一致模。例如, 考慮圖5表示的有界格L5, 在[e,1]上取三角余模Se=S∨, 在[0,e]上取表10定義的三角模Te。 圖5 有界格L5Fig.5 A bounded lattice L5 表10 [0,e]上的三角模TeTab.10 The t-norm Teon [0,e] 容易驗證, 對任意x∈Ie,y∈(e,1]有x 表11 L5上的二元算子U2Tab.11 The binary operator U2on L5 最后剩下的問題是: 當存在兩個元(x,y),(u,v)∈Ie×(e,1)使x1 預備知識
2 ?ayl所構造二元算子成一致模的新條件
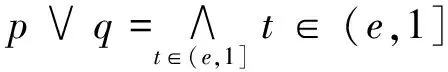







3 結語