一種基于卡爾曼濾波和序貫概率比檢驗的空氣彈簧泄漏故障預警方法*

楊 俊 薛明晨 祁 成

(南京中車浦鎮海泰制動設備有限公司， 211899， 南京∥第一作者， 高級工程師)

0 引言

空氣彈簧系統(以下簡稱“空簧系統”)[1-3]作為城市軌道交通車輛關鍵子系統之一，主要由AS(空氣彈簧)、差壓閥、高度閥等部件組成，是維持車體平衡穩定的重要部件。目前空簧系統的相關故障診斷方案較為簡單，這種比較原始的故障檢測方案不僅耗費了大量的人力物力，而且也不能捕捉相關部件可能存在的逐步耗損的過程。

針對這種問題，可以考慮通過一些智能算法來檢測空氣彈簧壓力，進而間接判斷出空簧系統是否存在故障。目前，采用智能算法檢測空簧故障的案列少之又少。而智能算法已經成功運用于存在泄漏故障的其他行業，如文獻[4]將SPRT (序貫概率比檢驗)應用于管道輕微泄漏，并驗證了SPRT在檢測小泄漏信號中的可行性。文獻[5]考慮到若單獨采用SPRT檢驗原始壓力信號，對于一些復雜的工況而言，其檢驗仍達不到滿意效果，因此采用卡爾曼濾波[6-7]突出原始壓力信號的拐點，并將處理得到的整條新息(卡爾曼濾波算法中測量方程的測量值與系統預測值的差值)信號作為SPRT的輸入，這兩種算法的有效結合取得了良好的檢測效果。然而，這種方法是提取離線數據的整條新息序列，并不能達到在線監測的要求。

綜上所述，本文提出一種基于卡爾曼濾波和SPRT的方法，用以檢驗空簧系統是否出現故障。該法不僅可對一些有輕微泄漏的故障進行及時的故障預警，而且可采用序列化新息輸入的方式進行在線故障檢測。該方法首先將同一轉向架的兩個空簧壓力進行求和后求其平均值；然后，采用卡爾曼濾波算法對取均值后的空氣彈簧壓力進行濾波處理，得到當前時刻的新息；最后，將標準化后的新息作為SPRT的輸入，通過SPRT檢驗當前時刻空簧系統是否出現故障。若無故障或不滿足SPRT作出判斷的條件，循環更新，判定下一時刻是否出現故障。本文所提算法的有效性在某地鐵運營車輛的采集數據中得到了驗證。該方法用于空簧系統相關部件的故障檢測有利于減少誤報，降低了維修成本。

1 城市軌道交通車輛空簧系統的工作原理和失效機理

空簧系統主要由空氣彈簧、差壓閥和高度閥3個部分組成，其目的是保持列車平穩運行，給乘客帶來良好的乘坐體驗感。現主要對空簧系統的工作原理和失效機理進行詳細描述。

1.1 空簧系統工作原理

空氣彈簧作為空簧系統最重要的部件，由氣囊、上蓋、扣環、節流阻尼裝置、輔助彈簧等組成，其結構如圖1所示。其中：氣囊作為空簧的核心部件，承擔主要的承載和減震功能；上蓋位于車體或搖枕下方，起密封和傳遞載荷的功能；扣環位于上蓋與氣囊之間，起密封和連接的功能；節流阻尼裝置與上蓋進氣口或支座連接在一起，起垂向阻尼作用；當氣囊損壞無氣時，輔助彈簧承擔起主要減震及承載功能。輔助彈簧又包含應急彈簧、支座、橡膠堆和緊固螺絲等部件。

圖1 空氣彈簧結構示意圖Fig.1 Diagram of air spring structure

1.2 空簧系統失效機理

空簧的失效機理較為復雜，大致包含4個類別：

1) 空簧氣囊故障。氣囊在使用中被人為或意外劃傷，使得膠囊出現裂紋；氣囊與上蓋板之間存在壓縮變形；長時間的接觸磨損會使膠囊破損；長期暴露在臭氧、日曬雨淋等環境中，使得氣囊出現鼓泡、龜裂現象。

2) 空簧上蓋故障。由于上蓋上部的橡膠墊尺寸不匹配或者上蓋受力不均勻等原因導致上蓋發生變形。此外，由于上蓋進氣口座與上蓋之間螺絲松動等原因，致使上蓋進氣口座與上蓋脫落。

3) 空簧橡膠堆、支撐座故障。由于長期的日曬、雨淋導致橡膠老化，從而使橡膠堆出現脫膠、裂紋現象。

4) 空簧節流阻尼故障。長時間浸泡在水中，致使節流阻尼裝置出現生銹現象，同時可能會引起彈簧支撐座等其他配件發生故障。

2 算法原理與故障預警實現過程

2.1 算法描述

2.1.1 卡爾曼濾波

對于1個時間序列的數據，假設t時刻的真實數據為Y(t){Y∈RM}，其中：R表示實數集，M表示數據的維度。設傳感器的測量數據為Ym(t)，當傳感器測量無漂移時，Ym(t)是Y(t)的1個無偏估計，即：

Ym(t)=FY(t)+ξ1

(1)

式中：

F——當前狀態到測量的轉換矩陣；

ξ1——期望為0、協方差為C1的高斯白噪聲。

當ξ1的方差較大時，測量數據對真實數據的估計效果不佳。因此，基于系統的原理方程：

Y(t)=AY(t-1)+Bu(t-1)+ξ2

(2)

式中：

Y(t-1)——t-1時刻的真實數據；

u(t-1)——偏置項；

A、B——均為轉移矩陣；

ξ2——期望為0、協方差為C2的高斯白噪聲。

由于Y(t-1)是未知的，Y*(t-1)為t-1時刻的最優估計，是已知的。假設方差為C*(t-1)，因此可以得到t時刻的預測值Yp(t)，它也是真實數據的另一個無偏估計：

Yp(t)=AY*(t-1)+Bu(t-1)

(3)

且可得Yp(t)的方差C+，t為：

C+,t=AC*(t-1)AT+C2

(4)

卡爾曼濾波的真正目的是根據t時刻真實數據的兩個無偏估計Ym(t)、Yp(t)來得到該時刻的最優估計Y*(t)。現做如下線性假設：

Y*(t)=Yp(t)+λ(t)(Ym(t)-Yp(t))

(5)

式中：

λ(t)——卡爾曼增益。

為了使Y*(t)成為真實數據的最優估計，應使Y*(t)的方差最小。通過求解Var(Y*(t))的最小值，最終可得：

λ(t)=C+,tFT(FC+,tFT+C1)-1

(6)

Var(Y*(t))=(I-λ(t)F)C+,t

(7)

式中：

I——單位矩陣。

將式(6)代入式(5)，可得到最優估計值Y*(t)。

2.1.2 序貫概率比檢驗

對于1個時間序列數據xi，假設其滿足方差為σ2的正態分布，現需要判斷該序列是否異常。設給出的原假設(系統運行正常)為H0，備選假設(系統運行異常)為H1。設μ0為H0下服從正態分布的均值，μ1為H1下服從正態分布的均值，Δμ=μ1-μ0。設α和β分別表示犯第1類錯誤(原假設正確卻拒絕原假設)和第2類錯誤(原假設錯誤卻未拒絕原假設)的概率。在H0和H1下，隨機時間序列的聯合概率密度為：

(8)

(9)

式中：

i——自然數序列；

n——xi的采樣總次數；

P0,n——H0下n次采樣的聯合概率密度；

P1,n——H1下n次采樣的聯合概率密度。

若滿足ω≥(1-β)/α，則認為隨機序列的聯合概率密度是P1,n的概率更大，則拒絕H0。若滿足β/(1-α)<ω<(1-β)/α，則不做判斷，繼續觀察，直到滿足ω≤β/(1-α)或ω≥(1-β)/α再作出判斷。

將xi進行標準化處理，并將式(8)～(9)代入β/(1-α)<ω<(1-β)/α，最終可化為遞推形式：

(10)

式中：

γ(n)——經過ω變換后的第n次采樣的檢驗參數；

γ(i) ——經過ω變換后的第i次采樣的檢驗參數；

γ(i-1)——經過ω變換后的第i-1次采樣的檢驗參數。

因此，實際檢驗時，只需計算出γ(i)的初值，即可通過遞推判斷系統是否異常。

2.2 故障預警的實現

卡爾曼濾波最終可得到修正序列X*(t)，但實際用于SPRT檢驗的并不是X*(t)，而是新息。定義新息e(t)為傳感器測量值Xm(t)與預測值Xp(t)之差，即：

e(t)=Xm(t)-Xp(t)

(11)

將此時的e(t)作為SPRT的輸入，通過序貫概率比檢驗即可判斷當前時刻t空簧系統是否存在泄漏現象。若無泄漏，則迭代計算下一時刻的新息，并代入SPRT判斷，重復此計算過程。

綜上分析，采用卡爾曼濾波和SPRT實現空簧故障預警的流程如圖2所示。

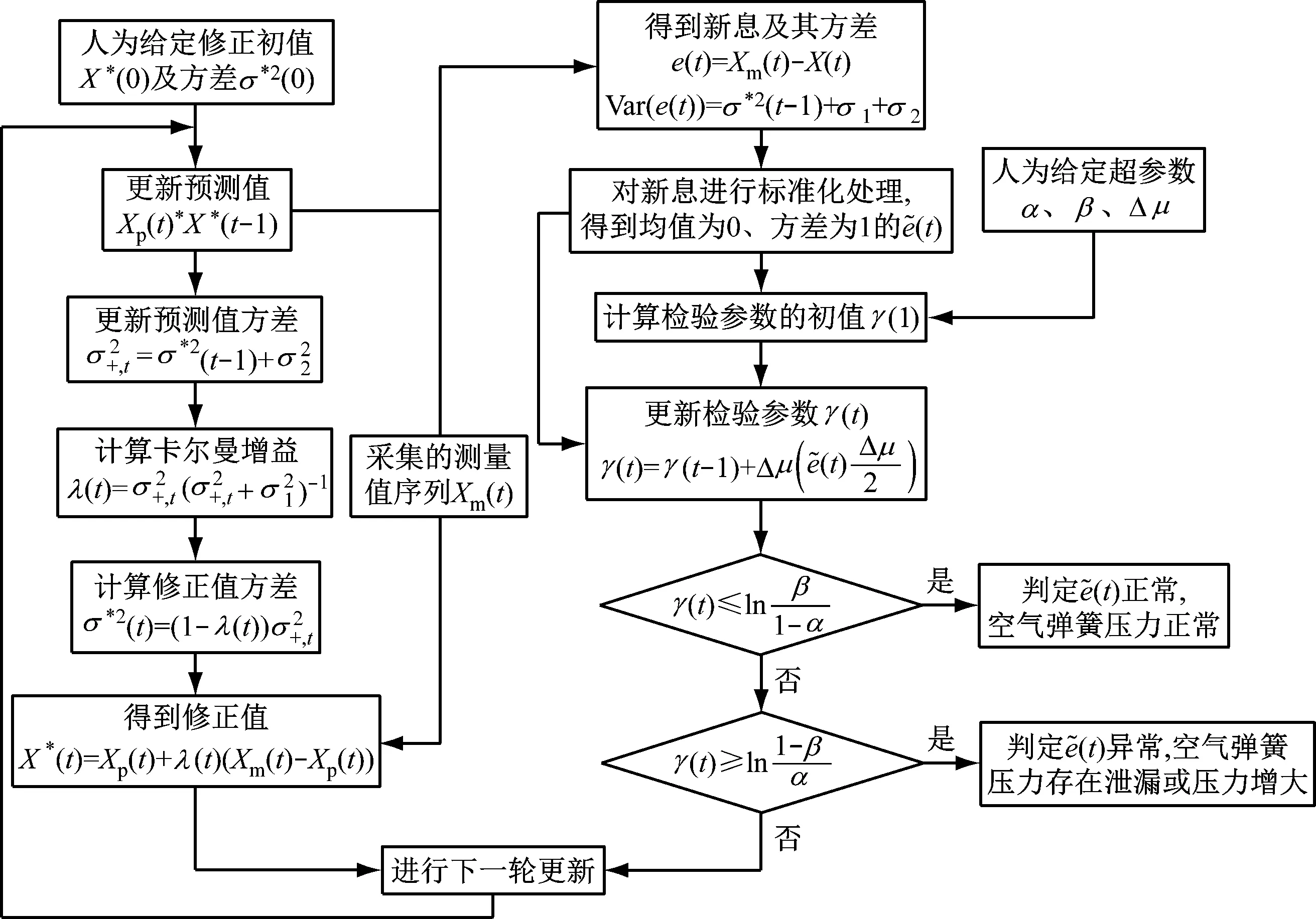
注：σ*2(t)——t時刻最優估計的方差；超參數指機器學習中在開始學習前已設置好的參數。圖2 基于卡爾曼濾波和SPRT的空簧故障預警流程圖Fig.2 Flowchart of air spring fault early warning based on Kalman filter and SPRT

3 數據驗證

為了驗證本文提出的算法的可行性，采用某地鐵運營車輛上采集到的96組數據，對該算法進行驗證，并采用EBCU (電子制動控制單元)邏輯檢測方法與本文所提方法進行對比。

將架控控制方式下制動控制系統單側的空氣彈簧壓力pAS,2代入EBCU邏輯檢測，檢驗出1組故障，結果如圖3所示。圖3共有120個采樣樣本，A點表示在該采樣時刻EBCU報出空氣彈簧壓力低故障。

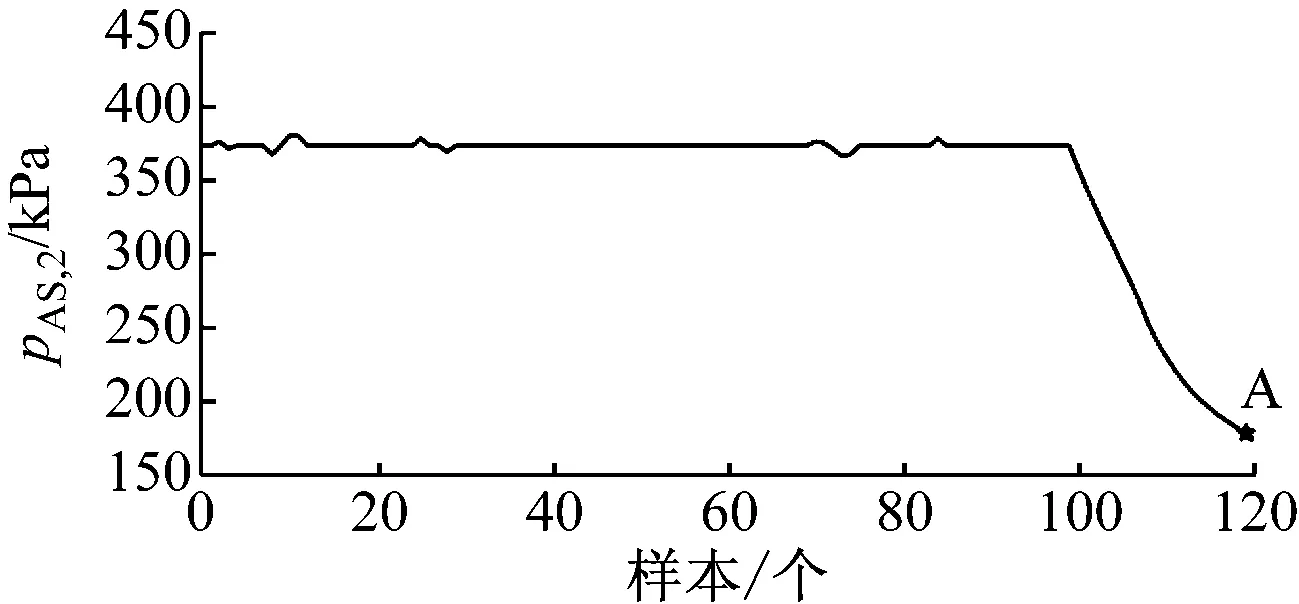
圖3 基于EBCU邏輯檢測方法的單側空氣彈簧壓力檢測結果Fig.3 Detection results of single-side air spring pressure based on EBCU logic detection mothed

設同一轉向架單側的兩個空簧壓力為pAS,1、pAS,2。如圖4所示，從96組車輛數據中隨機選取1組，得到所對應的pAS,1、pAS,2。從圖4可以看出：pAS,1與pAS,2并不相等，這是由于列車過彎、乘客分布不均等原因而引起的車輛兩側質量不相等。若直接將單側的pAS,1或pAS,2代入模型直接檢驗，則出現誤檢的可能性會很高，可能會致使檢驗模型失效，達不到預期目的。因此，將pAS,1、pAS,2累加后求出平均值pAS,a，將pAS,a作為模型的輸入。

a) pAS,1

如圖5所示，與單側的pAS,1、pAS,2相比，均值化后的pAS,a明顯更平穩，因此，采用均值化后的序列進行故障檢測更為合理。

圖5 均值化后得到的轉向架空氣彈簧壓力Fig.5 The air spring pressure of bogie after averaging

將均值化后的96組數據代入卡爾曼濾波和SPRT算法進行檢驗，其檢驗結果如圖6所示。圖6 a)中，縱坐標表示的是將SPRT檢驗參數γ經過區間處理變換為-1到1之間的檢測結果。當檢測結果為1時，表示空簧出現故障；當檢測結果為-1時，表示對空簧無故障。檢測結果在-1到1之間時，表示當前時刻采樣數據不作判斷。圖6 b)中，B、C、D為圖6 a)中檢驗結果為1時所對應的故障點。

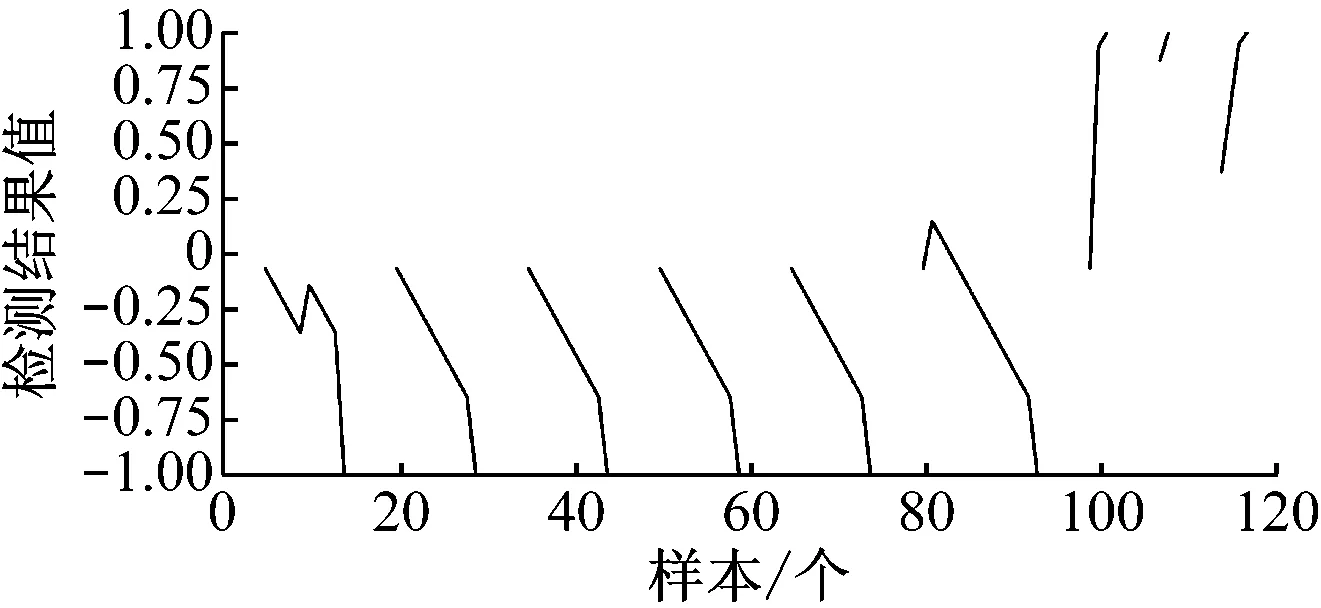
a) 檢驗參數γ經過區間變換后的檢測結果值

從圖6可以看出：樣本值為100個左右時，空氣彈簧壓力出現持續驟降的非正常情況，表明空氣彈簧發生了故障。然而基于現有EBCU檢測邏輯，需要再經過20個采樣點 (即樣本值為120個)后，空氣彈簧的泄漏量達到了報警條件，發出故障報警，存在明顯的時間延遲問題。與EBCU檢測邏輯相比，本文所提算法在空簧發生故障后的3個采樣時刻內立即報出故障。數據驗證結果表明：本文所提方法具有提前預警的功能。

4 結語

為了填補當前空簧系統故障診斷技術的空白，本文提出了一種基于序列化卡爾曼濾波和SPRT的空簧系統故障預警方法：通過卡爾曼濾波提取當前時刻空氣彈簧壓力的新息，將新息作為SPRT的輸入，通過SPRT判定空簧系統是否存在故障。以某地鐵運行車輛采集到的數據為案例，進一步驗證了該故障預警方法的有效性。該方法不僅能用于現車的在線監測，還能夠對輕微泄漏等故障進行提前預警，為城市軌道交通車輛空簧系統的故障診斷提供參考。