高中數學教學中對學生思維廣度與深度的思考
——以“正弦函數的性質與圖像”的教學為例

◎陳因鴻 （重慶市永川萱花中學校，重慶 402160）

引 言

進入高中階段，意味著學習者的學習能力與思考能力有著顯著的提升，他們能夠根據知識的內容構建完整的邏輯，并運用到實際當中.數學學科知識點之間的聯系較為緊密，以正弦函數為例，這部分知識不僅涉及與三角函數相關的內容，還包括函數圖像的變化，并能夠與余弦函數的性質和圖像形成對比.因此，通過介紹這部分內容，教師可以幫助學生更好地體會構建深度思維的意義，從而拓展思考的方向，將不同的知識連接成完整的知識網絡.在新的教育背景下，教師可以嘗試結合課外相關輔助資源，豐富授課環節，以保證學生的積極性.在學生自主學習能力提升的同時，培養他們的創新思維，最終使他們的能力和思維都有所提升.

一、思維廣度與深度的含義及意義

（一）具體含義

在全面培養與發展的過程中，教師應當首先明確培養的目標，從而制訂不同的授課方案.思維的廣度實際上是指橫向思考的能力，而深度則體現在集中思考的方向.廣度意味著學生要能夠多角度獨立地思考問題出現的原因、其中存在的規律和隱藏條件以及最終的解決方案，根據其中的一個已知條件，結合自己所掌握的知識進行突破，或者是在兩個相關聯的事物中探索其中的關系.這種思考的方式主要是要讓學生了解問題的多面性，從而培養他們舉一反三和一題多解的能力.深度更注重對結論的總結，通過事物的現象能夠挖掘出其內在的本質，這需要同學們對于不同的問題有著深刻的認識，由此找出合乎邏輯的關系.

（二）實際意義

面對新的教育形式，傳統教學已經不再適應現代學生的發展，數學的學習需要在練習習題的過程中總結出規律，這一切需要在知識扎實的情況下展開.因此，在課上，教師應當重視每一個單元之間存在的聯系，深入挖掘其中存在的規律，引導學生豐富自己的知識和閱歷，為思想的形成奠定基礎.而在課上培養思維的廣度與深度，真實的目的是要讓學生能夠深刻地理解知識的具體含義，能夠在現有的基礎上總結并創新，從而提高自己的思想境界與數學學科的核心素養，最終提升個人的能力.

二、高中數學教學中提升學生思維廣度與深度的思考

如今隨著教育體制改革的深入推進，越來越多的專家學者強調在高中數學教學中培養學生的核心素養，這就意味著教師在培養學生數學素養的同時，要提升學生思維的廣度與深度.筆者經過多年的教學實踐了解到，教師在培養學生思維廣度與深度的基礎上需要遵循以下教學原則：一、教學內容需要立足于學生的直觀想象力.二、教學內容需要能夠切實解決學生的數學疑問.三、教學活動需要立足于基本數學活動的經驗.以下將對這三個方面進行詳細的闡述與分析.

（一）立足于直觀想象力，培養學生的思維能力

實際上，在高中數學的教學過程中，教師需要培養學生的直觀想象能力.相比于高中其他科目的學習，數學學科具有一定的抽象性，學生在學習這部分內容時，如果無法在腦海中建立全面的想象，那么就無法充分理解該模塊內容.因此，專家將直觀想象力歸納到數學核心素養之中.筆者經過多年的教學實踐了解到，只有不斷提升學生的直觀想象力，才能夠有效提高課堂教學質量.直觀想象力不僅可以幫助學生將學到的知識轉化為數學思維，更能夠提升學生發現問題、解決問題的能力.值得注意的是，要想提升學生數學思維的廣度與深度，就需要在培養學生直觀想象力的過程中對這兩個方面足夠重視：一、直觀能力.二、想象能力.直觀能力的培養主要是培養學生建立直覺思維，想象能力的培養主要是培養學生的三維立體能力.因此，學生在學習數學知識時，需要在建立其直觀思維的基礎上有效培養其想象能力.

（二）立足于數學問題的解決，培養學生的思維能力

筆者通過一對一訪談班級中的學生，發現很多學生雖然能夠聽懂教師在課堂中傳授的知識，但是一到做題環節就手足無措.由此可見，在提升學生數學思維廣度與深度的過程中，還需要培養學生解決數學問題的能力.大多數學生無法將學到的知識轉化為解決問題的能力，這就要求教師在教學中融入適當的題型，從而達到培養學生思維能力的目的.如今，隨著素質教育的穩步推進，教師在培養學生解決問題能力的過程中，可以融入一些生活素材，這樣的方式不僅能夠有效提升學生的學習積極性，更能夠引導學生將教材知識與實際生活相結合，最終達到提升學生解決實際問題的能力.例如，在講解《正弦函數的性質與圖像》這一內容時，一些學生認為該知識十分晦澀難懂，學習久了甚至會出現走神的現象，因此，為了避免此類現象的發生，教師可以選取生活中的常見案例來進行教學.

（三）立足于基本數學活動的經驗，培養學生的思維能力

除了上述兩個方面之外，教師在提升學生數學思維廣度與深度的過程中，還需要立足于基本數學活動的經驗.研究發現，要想全面提升學生的數學核心素養，需要根據班級中學生的實際情況建立三維模型，通過分層抽樣測試的方式來對不同學生的數學核心素養進行分析，最終結果發現：對于大多數學生來說，他們的數學核心素養中抽象能力較好、邏輯能力較差，而學生的建模水平則呈現出參差不齊的情況.因此，在培養學生思維能力的過程中，教師需要有效提升學生的思維能力與建模水平.然而普通的教學無法對學生的這兩個能力進行有效提升，因此，教師需要立足于數學基本活動的經驗，根據班級中學生的實際水平選取更加符合班級學生能力的教學方式與活動形式，只有這樣的方式才能夠有效提升學生數學思維的廣度與深度.

三、理清知識結構拓展思想的廣度與深度

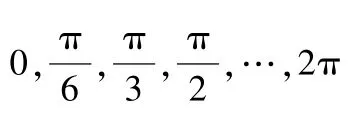
四、在實際教學中采用策略培養學生的專業思維

（一）情境建設

在課堂中，情境的建設能夠幫助學生更好地進入到相關的學習氛圍中.在帶領學生了解“正弦函數的性質與圖像”時，首先請他們思考“一個角的正弦是什么”，可以通過單位圓中正弦值的變化感受圖像的基本構成.如圖1 所示.

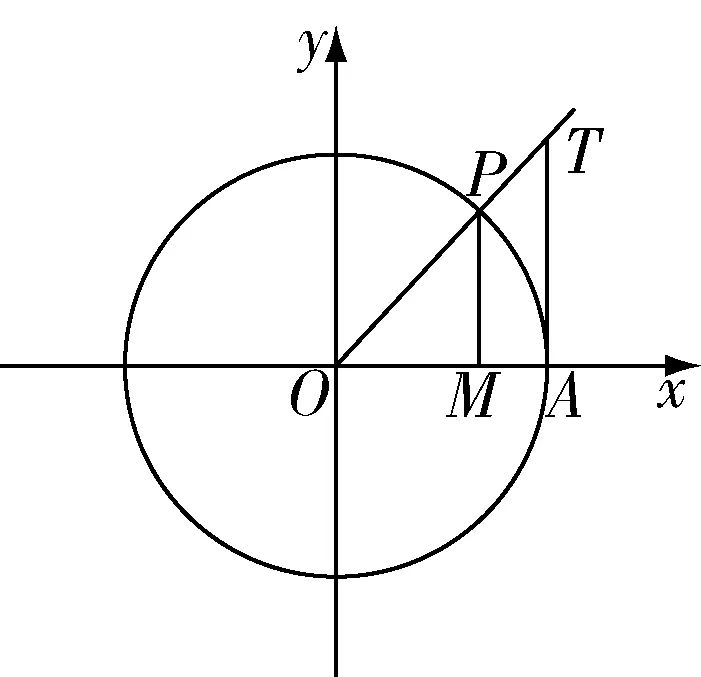
圖1

在這一單位圓中，代表圓的半徑，長度為1，根據正弦值的定義，圖中就是任意角度的正弦值.根據這一結論，請同學們思考：正弦值的取值范圍是什么？ 在思考中，學生能夠發現，隨著點的不斷運動，的值也在不斷地變化，取值區間為［-1，1］，將sin中的替換就能夠得出正弦函數，即＝sin，值域為［-1，1］，定義域為全體實數.這一概念的得出并不是教師直白地告訴學生的，而是他們自己總結出的.在這樣的情境建設中，學生可以根據最基礎的思路發現函數的定義式以及值域，在自己的總結中加深對這部分知識的理解與應用，由此發展其思維的廣度，找到知識間存在的聯系.之后，教師帶領學生共同研究圖像的畫法，學生首先能夠想到利用特殊的正弦值在坐標中描點，畫出一個單位區間的圖像.這種方法可以總結為“五點法”，（0，2π）為一個完整區間.在情境的建設中，學生的深度思維與廣度思維都能夠得到極好地訓練，從而發現數學的奧秘.

（二）思想提升

五、引導學生自主學習，拓展其思維的廣度與深度

結 語

邏輯的發展離不開教師和學生的相互配合，在實際的教學中，教師可以豐富課堂的環節帶動同學們主動思考，并在不同的提問方式中拓展同學們的思考方向，鍛煉學生的總結能力，在不同的方面中，培養他們思考的廣度與深度，從而更好地理解和應用這一數學知識.