解題教學中培養學生數學思維深刻性的途徑研究
◎趙 玲 王 淳 (.西華師范大學數學與信息學院,四川 南充 637000;.成都市新都一中實驗學校,四川 成都 60500)
一、思維深刻性品質的概述
數學思維品質的成分主要包括數學思維的深刻性、廣闊性、靈活性、獨創性、目的性、敏捷性和批判性七個方面.思維的深刻性又被稱為分清實質的能力,這種能力表現為能洞察所研究的每一事實的本質以及這些事實之間的相互關系.它是一切思維品質的基礎.對于初中學生而言,具備思維深刻性品質不僅是學生解題能力的基礎,也是學生終身學習所需的基本思維能力.因此,在初中教學中,培養學生思維深刻性至關重要.
二、培養學生思維深刻性品質存在的問題分析
由于思維的深刻性和解題能力之間有著密切聯系,解題能力是以思維的深刻性為基礎的,而學生思維深刻性的培養又是在解題過程中逐步實現的,因此教師應該在解題教學中有目的、有意識地對學生思維深刻性的品質進行培養.在習題的講解中,教師可通過區分相似概念、挖掘隱含條件、探索一般規律、滲透數學思想這四個途徑培養學生思維的深刻性.但是,在具體的解題教學中,許多教師卻忽視了通過這四個途徑.下面以反比例函數章節的習題為例,具體分析教師在解題教學中培養學生思維深刻性品質時存在的問題.
(一)忽視了對相似概念的區分
重視對相似概念的區分.教師可以使學生通過分析、比較相似事物屬性的異同,逐步培養學生透過現象看清問題本質的能力,提高思維的深刻性.但是,在反比例函數概念的解題教學中,許多教師沒有著重區分反比例函數和反比例關系的概念以及反比例函數值與正比例函數值的異同,學生在做題時極易對這些相似概念混淆,導致學生缺乏透過表面現象看清問題實質的能力,不利于學生思維深刻性的培養.
(二)忽視了對隱含條件的挖掘
隱含條件是指問題中那些若明若暗、含而不露的已知條件,往往需要通過對問題的深入分析和深刻理解才能使之明朗化.隱含條件的挖掘是對思維深刻性品質的鍛煉.但是,在求反比例函數值的解題教學中,許多教師認為學生遺漏隱含條件的原因是不細心,因此對隱含條件的講解存在“重結果”“輕過程”的現象.例如,題目中常需要根據圖形所在的象限決定值的符號以及在求反比例函數值時需要注意≠0.如果教師對詳細原因不做重點講解,那么學生解題時就容易漏掉這些隱含條件,導致學生解題的嚴謹性不能得到訓練,不利于思維深刻性的培養.
(三)忽視了對一般規律的探索
教師在講解同一類問題時,還要引導學生探討解決這類題型的“通法”,讓學生用異中求同的方式分析問題,揭示問題之間的相互關系,這本身就是對思維深刻性的訓練.但是,在求反比例函數與幾何圖形所圍成的面積的問題中,有的教師只是讓學生做例題,接著講例解.他們沒有對其中蘊含的解題規律進行歸納,進而總結出利用反比例函數值求面積問題以及利用坐標求面積問題的“通法”,導致學生缺乏用異中求同的方式分析問題和解決問題,不利于思維深刻性的培養.
(四)忽視了對數學思想的滲透
數學思想是數學的靈魂,是對數學知識本質的認識.注重數學思想的教學不僅能讓學生認識到數學知識的“軀體”,而且能使學生掌握其內在的“精神”,這也是對思維深刻性的訓練.但是,在解決反比例函數單調性問題的題目中,許多教師沒有滲透數形結合思想;在求不規則圖形面積問題的題目中,他們沒有滲透整體思想.這樣的做法導致學生不能將所學知識和方法進行有效的融合,缺乏對數學思想的構建,不利于思維深刻性的培養.
三、培養學生思維深刻性的途徑
上述內容分析了教師在解題教學中培養學生思維深刻性存在的問題.下面以反比例函數章節的典型習題為例,從注重區分相似概念、挖掘隱含條件、探索解題規律、滲透數學思想這四個途徑提出培養學生思維深刻性的方法.
(一)注重區分相似概念
概念是對事物本質屬性的描述,重視相似概念的區分能夠加深學生對事物本質的認識.在教學中通過比較、分析相似概念的異同點,能夠避免學生被事物表面的相似性迷惑,從而提高學生分清相似事物實質的能力,達到培養學生思維深刻性的目的.
1.區分反比例關系和反比例函數的概念.
例1 下列屬于反比例函數的是( ).

由于反比例函數與反比例關系概念的相似性,許多學生不能區分反比例函數與反比例關系的異同,誤認為最后兩個選項也是反比例函數.事實上,反比例函數中兩個變量只能由單獨的字母表示,而反比例關系中的兩個變量是整式.因此反比例函數是反比例關系的一種特殊情況,并且反比例函數中的兩個變量有更明確的數量關系.教師通過對反比例函數概念和反比例關系概念的教學,可以提高學生在認知結構中對反比例函數概念的認知.
2.區分反比例函數值與正比例函數值的概念.



(二)注意挖掘隱含條件
隱含條件是那些隱含在題設內,不易被察覺的條件.在教學中,教師可通過挖掘隱含條件,使題設條件更完備,這有利于提高學生分析問題的嚴謹性.因此,注意隱含條件的挖掘也是對思維深刻性的培養.
1.注意≠0.
很多學生根據-5=-1,得出=±2.而忽略了≠2.在教學中,教師要深入挖掘反比例函數≠2 的含義.因為當=2 時,無論取何值都有≡0,不滿足反比例函數的定義.通過分析本題中≠2 這一隱含條件,可提高學生分析問題的嚴謹性.
2.注意的符號.

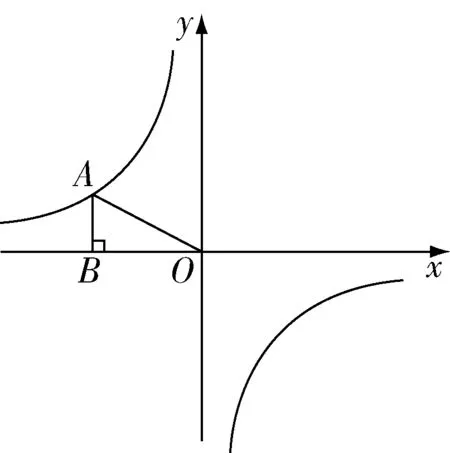
圖1
A.-6B.6C.-3D.3
很多學生根據三角形面積為3,得出=6,忽略了還要結合函數圖像所在的象限確定的符號.在教學中,教師要深入分析三角形面積和的幾何意義的聯系,才能使學生避免這類問題設下的陷阱,提高學生解題時的嚴謹性.
(三)注重探索解題規律
對反比例函數求面積問題的綜合題進行分析,可以發現這類題的題目雖然變化多端,但是關鍵考點并不多,很多題看似不同,其實屬于同一類題.通過探討解決一類題的“通法”,用異中求同的方式分析問題、揭示問題之間的相互關系,就是對思維深刻性的培養.
1.探索利用反比例函數值求面積問題的解題規律.

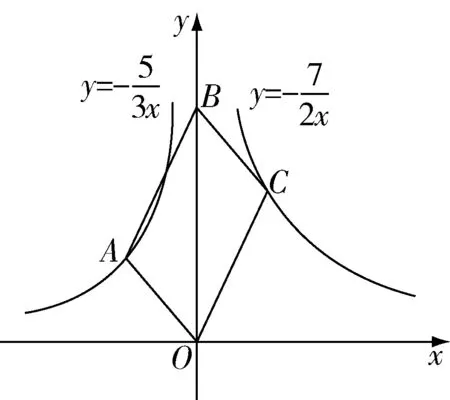
圖2
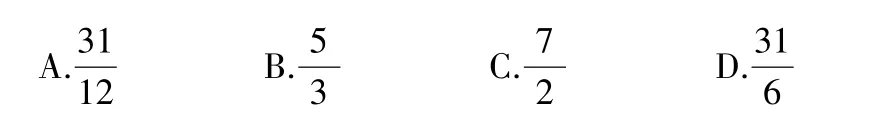
如果題目的已知量只有函數解析式,則這類問題就要利用反比例函數值求解.雖然本題是用值求面積問題的個別案例,但教師要引導學生探索出解決這類問題的一般規律.通過對該案例解題環節的提煉,學生不難發現這類問題的解題規律:首先觀察所給圖形的任意一邊是否垂直坐標軸,如果垂直,則可直接利用值求解.如果所給圖形的任意一邊不垂直于坐標軸,則要利用三角形全等的知識,將原圖形進行割補,轉化為任意一邊垂直坐標軸的圖形,再利用值求解.
2.探索利用坐標求面積問題的解題規律.

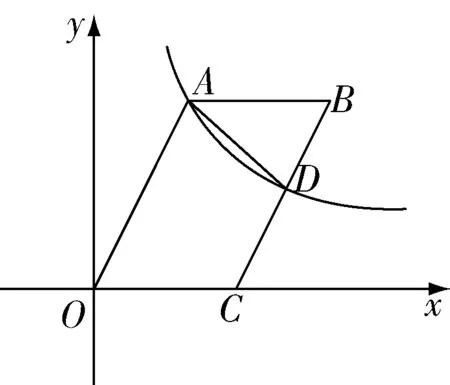
圖3

如果題目的已知量只有函數解析式、點的坐標,則這類問題就要利用點的坐標求解.本題盡管是用坐標求面積問題的特殊案例,但教師要引導學生探索出解決這類問題的一般規律,通過對該案例解題環節的提煉,學生不難發現這類問題的解題規律:根據已知點的坐標及其函數解析式可求出其他關鍵點的坐標,再將這些點的坐標關系轉化為線段關系,結合面積公式,從而將問題解決.
(四)注重滲透數學思想
數學思想是學生依據具體的數學內容在認知結構中提煉出的數學本質.在解題過程中,數學思想是學生明確解決問題方法的認知能力,是使學生分清問題實質的必備要素.因此,數學思想的滲透在思維深刻性的培養中必不可少.
1.滲透數形結合思想.
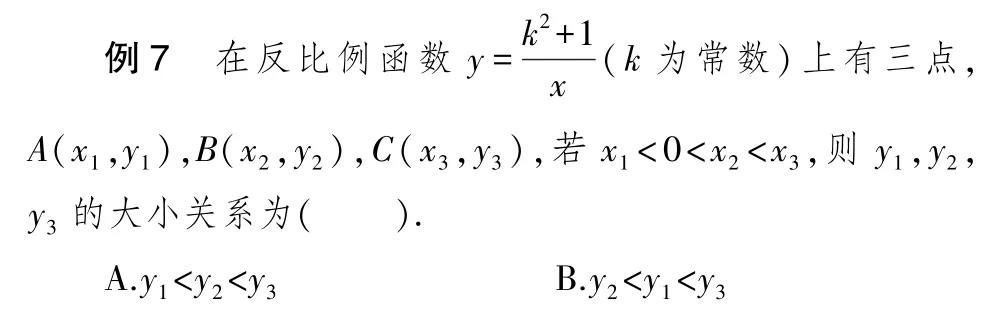

在講解有關函數單調性的題目中,要結合函數圖形分析題目.通過函數圖像判斷函數值的大小,可使學生領悟數形結合思想,體會數學的本質.
2.滲透整體與系統思想.

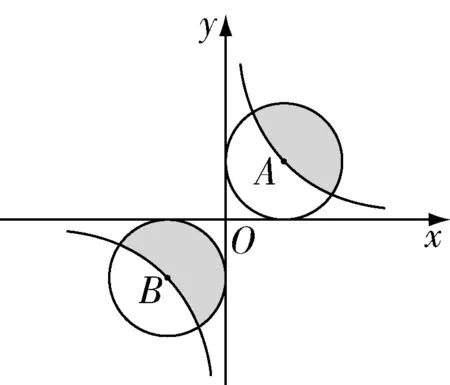
圖4
由于反比例函數具有關于原點中心對稱的性質,如果所求的圖形也具有對稱性,那么從整體與系統的角度認識反比例函數圖像和幾何圖形,就是對這類題型本質的認識.本題解題的關鍵在于要將題目中所給圖形的某一部分,利用對稱性轉化為一個整體圖形,這里的整體圖形是指能夠利用基本圖形的面積公式計算出面積的圖形.通過領悟整體與系統思想,學生能體會到解決這類問題的本質.
結 語
教師應該有目的、有針對性地對學生思維的深刻性品質進行培養.本文提出了在解題教學中從注重區分相似概念、挖掘隱含條件、探索解題規律、滲透思想方法這四個途徑培養學生思維深刻性的方法.首先,教師應該注重相似概念的區分,提高學生分清相似事物實質的能力;其次,注重隱含條件的挖掘,提高學生分析問題的嚴謹性;再次,注重對同一類問題解決規律的探索,提高學生用異中求同的方式分析問題的能力;最后,注重數學思想的滲透,對題目中蘊含的數學思想建立整體性的認知結構.這四個途徑,不僅能幫助教師優化教學策略,提高解題教學的效率,而且能幫助學生開拓思維,提高學生分析問題和解決問題的能力,使學生具備終身學習的思維品質.

