墻壁開關按鈕卡扣的扣合量對脫扣力的影響研究

吳禮紅 馬 騰 姚思捷 張 宇 王萬松

（公牛集團股份有限公司 慈溪 315314）

引言

按照企業標準，為保障墻壁開關產品在使用過程中的可靠性以及可維修性，要求墻壁開關按鈕在撥打使用的過程中不會輕易脫扣，以及按鈕在維修時便于拆卸，本公司規定按鈕的脫扣力在10 ～45 N 之間。通常，按鈕脫扣力的定義是指縱向脫扣力，如圖1所示。本文的脫扣力專指按鈕的縱向脫扣力。

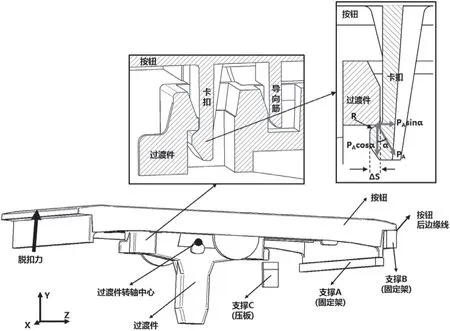
圖1 分析結構的示意圖

影響按鈕脫扣力的因素很多，其中爭議最大的就是按鈕卡扣的扣合量△S（指按鈕卡扣與過渡件卡扣的過盈量，如圖1所示）。眾所周知，按鈕卡扣的扣合量對按鈕脫扣力影響很大，但是不知道具體影響多大，而且不知道最理想的卡扣扣合量是多少。扣合量不是越大越好，扣合量太大，脫扣力太大，卡扣容易斷；扣合量也不是越小越好，扣合量太小，尺寸公差對脫扣力影響可能很大，脫扣力波動太大。可是從來都沒有精確的數據依據來支持這些結論，不知道卡扣的扣合量設計多少合適。依據多年的歷史經驗，目前卡扣的扣合量設計為0.4 mm，到底是不是最佳的？本文借助FEA 軟件的結果和力學理論予以解答。

1 受力分析

如圖2所示。按鈕在受到脫扣力P1作用時，在卡扣A 和B 處受到過渡件的接觸力PA和PB，向X1,Z1 方向分解，得PAsinθ，PAcosθ，PBsinθ 和PBcosθ，按鈕底部受到固定架的支反力P2。脫扣力P 對按鈕底部接觸線的Y1 方向力矩等于PA，PB對按鈕底部接觸線的Y1 方向力矩之和。見公式（1）。

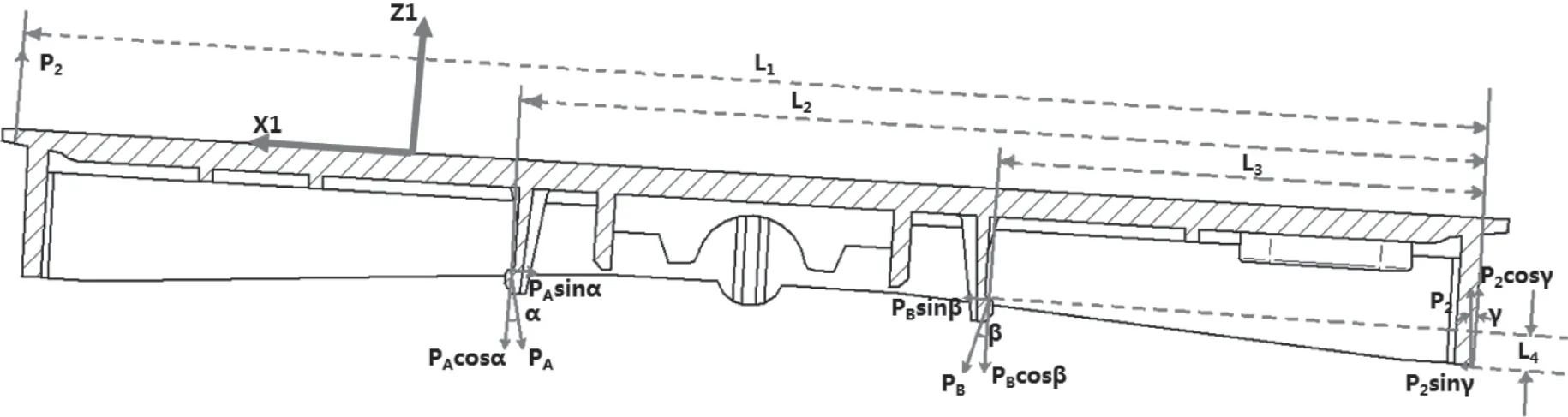
圖2 按鈕受力分析圖

式中：

P1—按鈕脫扣力；

PA—過渡件對按鈕的接觸力，與Z 軸夾角α，位于靠近脫扣力一端；

PB—過渡件對按鈕的接觸力，與Z 軸夾角β，位于靠近固定架對按鈕支反力一端；

P2—固定架對按鈕下邊緣的支反力。

如果忽略P2與Z 軸的夾角γ，為了保持X 方向的力平衡，有式（2）：

由于過渡件自身要保持力矩平衡，所以有式（3）：

由（2）/ （3）可得，α=β，以及PA=PB。于是式（1）可以簡化為

如果繼續忽略按鈕在過渡件附近的彎曲變形，可以近似有式（5）：

式中：

△S—按鈕卡扣的扣合量；

K—按鈕卡扣的沿X 方向受力的剛度，在小變形范圍內，近似假定恒定。

將式（5）代入（4），得

如果假設在不同的脫扣力作用下，α 變化不大，則式（6）揭示出脫扣力P1與卡扣扣合量△S 之間成線性關系。以下將用FEA 計算數據來驗證該結論是否正確。

2 按鈕脫扣力的FEA 仿真分析與試驗對標

2.1 FEA 仿真分析的準確度的影響因素與控制

CAE（仿真分析，包含FEA 和CFD 分析等）技術發展至今日，雖然已經取得很多輝煌的成就，但是離成熟還差距甚遠，最大的問題在于計算的準確度很難保證，與試驗值差距有時很大。其原因有很多,首先商用CAE軟件的歷史還很年輕，很多頂尖軟件才三四十歲，而且很多復雜問題只能用一到兩款頂尖軟件才算得比較準確。更何況，在某些方面CAE 軟件基于的力學理論本身就不夠成熟，比如多軸疲勞理論。還有就是CAE 軟件的具體設置步驟多，難度大。

具體來講對于靜態固體力學（不含疲勞）FEA 分析，其準確度有以下14 種影響因素：

1）使用的FEA 軟件計算能力的強大程度；

2）FEA 軟件所基于的力學理論的成熟度；

3）FEA 分析所使用的3D 模型的準確度；

4）FEA 分析的約束是否恰當；

5）FEA 分析的載荷是否與實際吻合，是否有意外載荷；

6）FEA 分析的接觸是否足夠多，接觸設置是否正確；

7）FEA 分析的材料參數是否準確；

8）FEA 分析的摩擦系數是否準確；

9）FEA 分析的網格密度是否足夠；

10）FEA 分析的網格外形是否合格；

11）FEA 分析的網格階數是否足夠；

12）實際結構的材料是否有缺陷，損傷；

13）實際結構是否漏裝或裝錯了零件；

14）實際結構的裝配預緊力矩等裝配工藝是否正確。

很多中國CAE 工程師，甚至國外一流企業的CAE工程師會自我安慰，說CAE 的計算結果與試驗值不吻合是很正常的，獲取輸入數據本身就很困難，而且用同一種CAE 分析方法來計算A 和B 兩種不同的產品，即使這種CAE 分析方法與實際有偏差，但是偏差的百分比應該是差不多的，比如差距x %，至少A 和B 兩種產品的力學性能誰高誰低可以計算出來。就像用一把有問題的尺子量不同的東西比長短，就算尺子的每個刻度都同時偏小或偏大，它也能用于不同產品進行長短對比。但是，他們忽略了一個問題：誰能證明A 和B 的CAE 計算結果與實際的差距都是x %？難道不會一下子80 %，一下子50 %，一下子-10 %？沒人可以證明，只是你自己的假設。而且用每個刻度有恒定偏差的尺子來比喻不準確的CAE 分析本身就是重大錯誤，因為CAE 分析的影響因素非常多，而不是僅僅像每個刻度都等比例偏差這么簡單，未經研究，一個不準確的CAE 分析與實際的偏差根本無法假設為恒定。

但是，如果一個相對很準確的CAE 分析方法，針對不同的產品每次的計算結果都能控制在10 %左右，在工程應用上我們是可以勉強忽略這種差距的。

要實現一種CAE 分析方法每次都能與實際偏差10 %左右，需要對以上14 種影響因素的每一種都了如指掌，精確控制，通常這需要非常深厚的力學理論，非常豐富的工程經驗，以及非常艱苦的數據采集和研究工作，花費大量的時間和精力去研究才能實現。就像產品工程師分析研究產品的失效投訴一樣，非常難，非常費神。

但是為了發揮CAE 分析的潛在價值，真正做到CAE替代試驗，甚至CAE 驅動設計，引領設計，試驗對標的準確度是第一關要過的，而且必須要過。

2.2 FEA 的模型及加載

FEA 模型如圖2所示，在圖2所示位置施加垂直按鈕邊緣平面向上的脫扣力。

2.3 FEA 分析所使用的材料參數

本文研究的按鈕的材料是PC，通過注塑成型的方式制造。但是高分子材料的注塑條件，比如注塑壓力和注塑速度，均會對注塑件的彈性模量造成很大影響[3]。

經實測，FEA 分析所使用的材料參數如下，計算剛度時FEA 軟件只需要輸入彈性模量E=1 970 MPa，泊松比μ=0.39，剪切模量G 無需輸入，FEA 軟件會根據E和μ 自動計算出G[1]。

2.4 按鈕脫扣力試驗與FEA 結果對比

由于高分子材料具有粘彈性，測試的時間將對結果影響明顯[2]，本文對測試時間的規定為5 s 內測量力值。

某型開關的脫扣力試驗值如表1所示，FEA 計算值與之非常接近，說明本文上述脫扣力FEA 計算方案是可靠的。

表1 按鈕脫扣力(Y 方向)的FEA 計算值和試驗值

3 按鈕卡扣扣合量對按鈕脫扣力的影響研究

3.1 按鈕卡扣扣合量對按鈕脫扣力的影響曲線

讓卡扣扣合量在（0.1 ～0.5）mm 之間變化，用FEA軟件進行計算出其對應的脫扣力值，繪制出按鈕卡扣扣合量對按鈕脫扣力的影響曲線，如表2和圖3所示。

圖3 ΔS 對開關按鈕脫扣力的影響

可以發現當卡扣扣合量大于等于卡扣接觸圓角（R=0.2 mm）時，卡扣扣合量對按鈕脫扣力的影響曲線近似是一條直線，本文推導的公式（6）預測該影響曲線也是直線，公式（6）預測的曲線趨勢是對的。但公式（6）預測出：當卡扣扣合量△S=0 mm 時，按鈕脫扣力才是0 N，然而實際上FEA 算出：按鈕脫扣力在△S=0.1 mm 時，就已經接近0 N。出現這種偏差是因為卡扣的接觸圓角對扣合量有削弱作用，當卡扣扣合量小于卡扣接觸圓角（R=0.2mm）時，這種削弱作用尤其明顯，這是造成公式（6）的計算結果與FEA 結果不符的原因，后續需要繼續研究卡扣的接觸圓角對扣合量有削弱作用。

3.2 按鈕卡扣扣合量對按鈕脫扣力的影響敏感度曲線

變量對應變量的影響敏感度定義為應變量的變化率/變量的變化率。

根據表2影響敏感度的計算結果，繪制出按鈕卡扣扣合量對按鈕脫扣力的影響敏感度曲線，如圖4所示。

圖4 ΔS 對開關按鈕脫扣力的影響敏感度曲線

表2 ΔS 對開關按鈕脫扣力的影響敏感度

可以發現按鈕卡扣扣合量對按鈕脫扣力的影響面敏感度≥1，屬于高度敏感。

4 優化建議

4.1 卡扣扣合量設計過大對產品性能的影響

1）卡扣扣合量設計過大，將造成按鈕脫扣力過大，而且按鈕在注塑成型過程中，勢必發生縮水，翹曲，變形等現象，對尺寸造成一定偏差，可能加大脫扣力；注塑成型也會影響結構的彈性模量[3]，對脫扣力造成影響，可能加大脫扣力；還有一些其它因素會造成脫扣力飆升，比如接觸圓角太小等。所以卡扣扣合量不宜設計過大，一般25 N 左右為宜。

2）如果扣合量設計過大，為了保證脫扣力不過大，一般會降低按鈕卡扣的剛度，也就是降低卡扣背部加強筋的高度H，如圖5所示，這樣會增加卡扣的應力，降低卡扣的強度，更容易斷裂，當按鈕進行噴漆后，材料的強度大幅度降低，按鈕就很有可能斷裂，見圖5所示。目前卡扣的扣合量為0.4 mm，脫扣力為22.9 N，卡扣根部截面已經有微小面積屈服（基于未噴漆的PC 的屈服強度），如圖5所示，不宜再繼續降低卡扣背部加強筋的高度，否則卡扣應力過大。

圖5 按鈕脫扣瞬間卡扣的應力

4.2 卡扣扣合量設計過小對產品性能的影響

圖紙上卡扣間距L 的公差是±0.1 mm，則卡扣扣合量ΔS 的公差可以認為是±0.05 mm。如果卡扣扣合量設計成0.3 mm，卡扣的實際最小扣合量是0.25 mm。一般而言卡扣的接觸圓角R 認為是0.2 mm，如圖1所示，這樣扣除接觸圓角R 后，真正有效的扣合量就微乎其微，可能造成脫扣力小于10 N 的不合格下限。所以目前卡扣扣合量設計值0.4 mm 是最佳的（在卡扣的接觸圓角為0.2 mm 的條件下）。

5 小結

本文對按鈕卡扣的扣合量對按鈕脫扣力的影響進行了研究，首先利用FEA 軟件計算了按鈕的脫扣力，并充分驗證影響FEA 軟件計算結果的6 大輸入參數：網格，接觸，約束，載荷，材料參數，摩擦系數等，以使FEA結果與試驗值差距在10 %左右。然后利用該準確的FEA分析模型，分析了不同按鈕卡扣的扣合量對按鈕脫扣力的影響曲線和影響敏感度曲線。最后結合該影響曲線，分析了卡扣扣合量過大和過小按鈕脫扣力的不利影響，最后得出卡扣扣合量的經驗值0.4 mm 是最佳值（在卡扣的接觸圓角為0.2 mm 的條件下）的結論。

本研究證明了FEA 力學分析技術可以非常高效快速地協助設計，幫助解決產品力學性能問題，輔助研究產品的改善方向，是值得電工行業大力推廣的高科技研發技術。