SMC 高壓變頻模塊隨機振動疲勞分析

鄒華民，周曉云，曹強，高原，孫保濤

（株洲中車時代電氣股份有限公司，株洲 412001）

引言

功率模塊作為高壓變頻器的核心功能單元，其振動環(huán)境適應性對于變頻器的安全運輸和正常工作至關重要。在變頻器從制造工廠運輸至安裝現(xiàn)場時，路面不平坦等因素產(chǎn)生的隨機振動會通過車輛的輪胎、懸掛系統(tǒng)和車身激勵作用于機組中的功率模塊。這些隨機振動可能導致高壓變頻模塊殼體的疲勞破壞、電氣部件的損壞失靈等——根據(jù)以往對電子設備大量的故障失效統(tǒng)計證明：因環(huán)境因素引起的故障失效占電子設備故障失效數(shù)的50 %左右，其中運輸?shù)犬a(chǎn)生的振動與沖擊占比15 %以上[1]。因此，有必要通過仿真分析的方式來評估模塊在實際運輸工況下的隨機振動響應及其疲勞損傷情況。

高壓變頻模塊的殼體零部件采用電氣、力學等綜合性能優(yōu)良的復合材料——不飽和聚酯玻璃纖維增強片狀模塑料（以下簡稱SMC 材料）模壓成型制成。通常，復合材料的阻尼系數(shù)可達0.05，其制品擁有良好的減振降噪效果[2]。然而，目前對于該類SMC 模塊結構的阻尼比大小仍未具體明確，這一關鍵仿真輸入?yún)?shù)對模塊隨機振動疲勞仿真結果的準確性影響很大。因此，需要開展相關試驗來對比驗證仿真模型，在仿真結果與試驗結果整體趨勢一致的前提下，進一步修正確定該類SMC 模塊結構的阻尼比大小，從而保證仿真結果的準確性和可靠性，并為后續(xù)該類SMC 模塊結構甚至變流器柜體結構的仿真分析提供準確輸入?yún)?shù)。

本文針對SMC 高壓變頻模塊在實際運輸過程中的隨機振動工況，利用HyperMesh 軟件和ANSYS 軟件仿真分析了模塊的隨機振動響應及其疲勞損傷情況，并通過試驗對比驗證了仿真分析模型，在仿真結果與試驗結果整體趨勢一致的前提下，進一步修正確定了該類SMC 模塊結構的阻尼比大小。

1 隨機振動疲勞仿真分析

1.1 仿真分析流程與方法

隨機振動疲勞仿真分析一般分三步進行。首先對有限元模型進行頻率響應分析，計算得到模型的應力傳遞函數(shù)（即模型受單位載荷激勵時其在各階固有頻率上的應力分布情況）；然后將應力傳遞函數(shù)乘以載荷功率譜密度，即可獲得模型的應力響應功率譜密度，再通過雨流計數(shù)法模擬得到應力概率密度函數(shù)（PDF）；最后利用材料的應力-壽命曲線（即S-N 曲線），基于Miner線性疲勞損傷累積理論進行疲勞損傷估計[3]。其中，前兩步已在ANSYS 等有限元軟件中成熟集成，本節(jié)主要介紹第三步的疲勞損傷估計理論和方法。

Miner 理論基于三個假設：①在任意等幅加載情況下，材料在每一應力循環(huán)里吸收等量凈功，當這些凈功累積至臨界值時，材料即發(fā)生疲勞破壞；②不同等幅及變幅加載情況下，材料疲勞破壞時吸收的臨界凈功相等；③變幅加載情況下，材料各級應力循環(huán)吸收的凈功相互獨立，且與各級應力循環(huán)的加載次序無關。從這些假設出發(fā)，若材料疲勞破壞時可吸收的臨界凈功為W、總應力循環(huán)數(shù)為N，在某級應力循環(huán)σi的循環(huán)數(shù)為ni、吸收的凈功為Wi，則材料吸收的凈功與其循環(huán)數(shù)之間存在正比關系，即：

若材料的加載歷史由σ1、σ2、…、σm共m 個應力循環(huán)等級構成，各級應力循環(huán)下的循環(huán)數(shù)和疲勞壽命分別為n1、n2、…、nm和N1、N2、…、Nm，則疲勞損傷D 為：

當D=1 時，材料吸收的凈功達到臨界值W，材料發(fā)生疲勞破壞。

上述計算過程中，假定了應力歷程是固定幅值，當應力歷程是隨機過程時，疲勞損傷計算相對比較復雜困難。在對應力響應分布情況的多種處理方法中，Steinberg提出的基于高斯分布的三區(qū)間法比較簡單實用，已廣泛應用于航天電子工業(yè)等領域。該方法認為，結構內(nèi)部各處的應力響應近似服從高斯分布，即應力響應值小于1σ 的概率約為68.3 %，大于1σ 且小于2σ 的概率約為27.1 %，大于2σ 且小于3σ 的概率約為4.33 %，大于3σ 的概率極小，可以忽略不計。因此，在利用Miner 理論進行疲勞損傷計算時，可將應力嚴重部位的應力響應處理成小于1σ、大于1σ 且小于2σ、大于2σ且小于3σ 三個應力水平。顯然，結構在受載時間T內(nèi)的總疲勞損傷為：

式中：

n1σ—小于1σ 應力水平的實際循環(huán)數(shù)（0.683υ+T）；

n2σ—大于1σ 且小于2σ 應力水平的實際循環(huán)數(shù)（0.271υ+T）；

n3σ—大于2σ 且小于3σ 應力水平的實際循環(huán)數(shù)（0.043 3υ+T）；

N1σ、N2σ和N3σ—根據(jù)材料S-N 曲線查得的1σ、2σ 和3σ 應力水平下的許可循環(huán)次數(shù)；

υ+—各級應力循環(huán)的統(tǒng)計平均頻率。

1.2 模塊結構組成及材料參數(shù)

高壓變頻模塊殼體主要由主箱體、前面板、右側板和外掛基座等組成，各零部件通過螺栓組裝連接緊固；模塊電氣部件主要有IGBT 元件、散熱器、電容、單元控制板和銅排等。

模塊殼體零部件均采用SMC 材料模壓成型制成。由于SMC 材料在片材制作時，是將短切玻璃纖維均勻拋灑在樹脂糊中制成，所以從宏觀上可將SMC 材料看作一種相對意義上的各向同性復合材料，且具備線性力學性能[4]。表1 所示為SMC 材料的基本性能參數(shù)[5]，由于缺乏SMC 材料的實測S-N 曲線，本文利用其基本力學性能參數(shù)及通用的材料疲勞壽命模型推算獲得其S-N 曲線，如圖1 所示；此外，因該類SMC 模塊結構的阻尼比大小仍未具體明確，其阻尼比暫時采用復合材料的保守估計值0.05。

表1 SMC 材料的基本性能參數(shù)

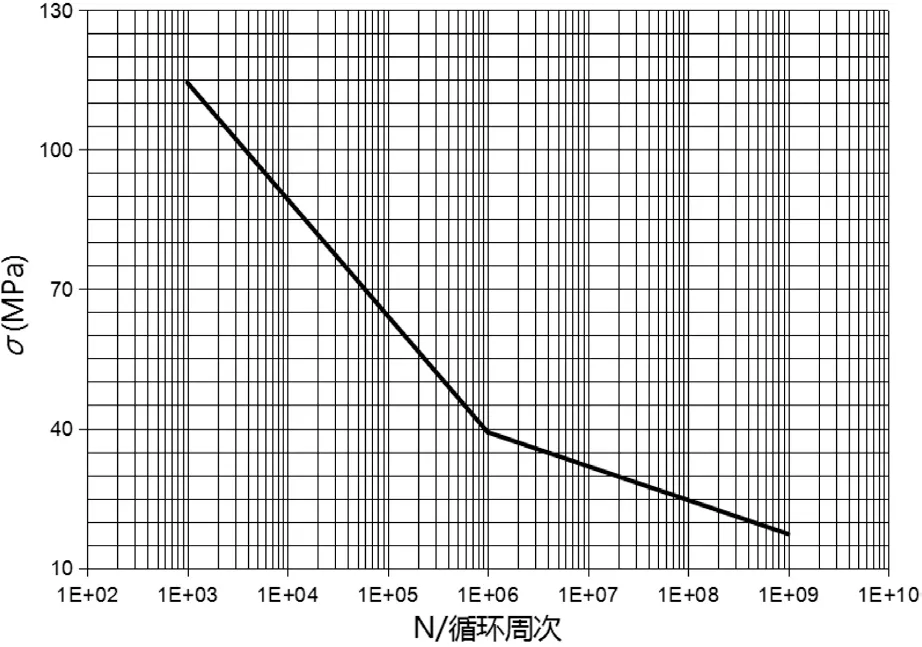
圖1 SMC 材料的S-N 曲線

1.3 模塊有限元模型、邊界條件及載荷輸入

由于模塊結構不完全對稱，故取整體結構建立有限元模型，圖2 所示為利用HyperMesh 軟件建立的模塊有限元模型，其中X 方向為橫向，Y 方向為縱向（車體行進方向），Z 方向為垂向。網(wǎng)格劃分時，模塊殼體各零部件以六面體實體單元為主，極少數(shù)為棱柱體實體單元；電氣部件等效為重心位置的質(zhì)量點，通過質(zhì)量單元模擬；螺栓連接采用剛性連接單元和梁單元組合等效模擬。

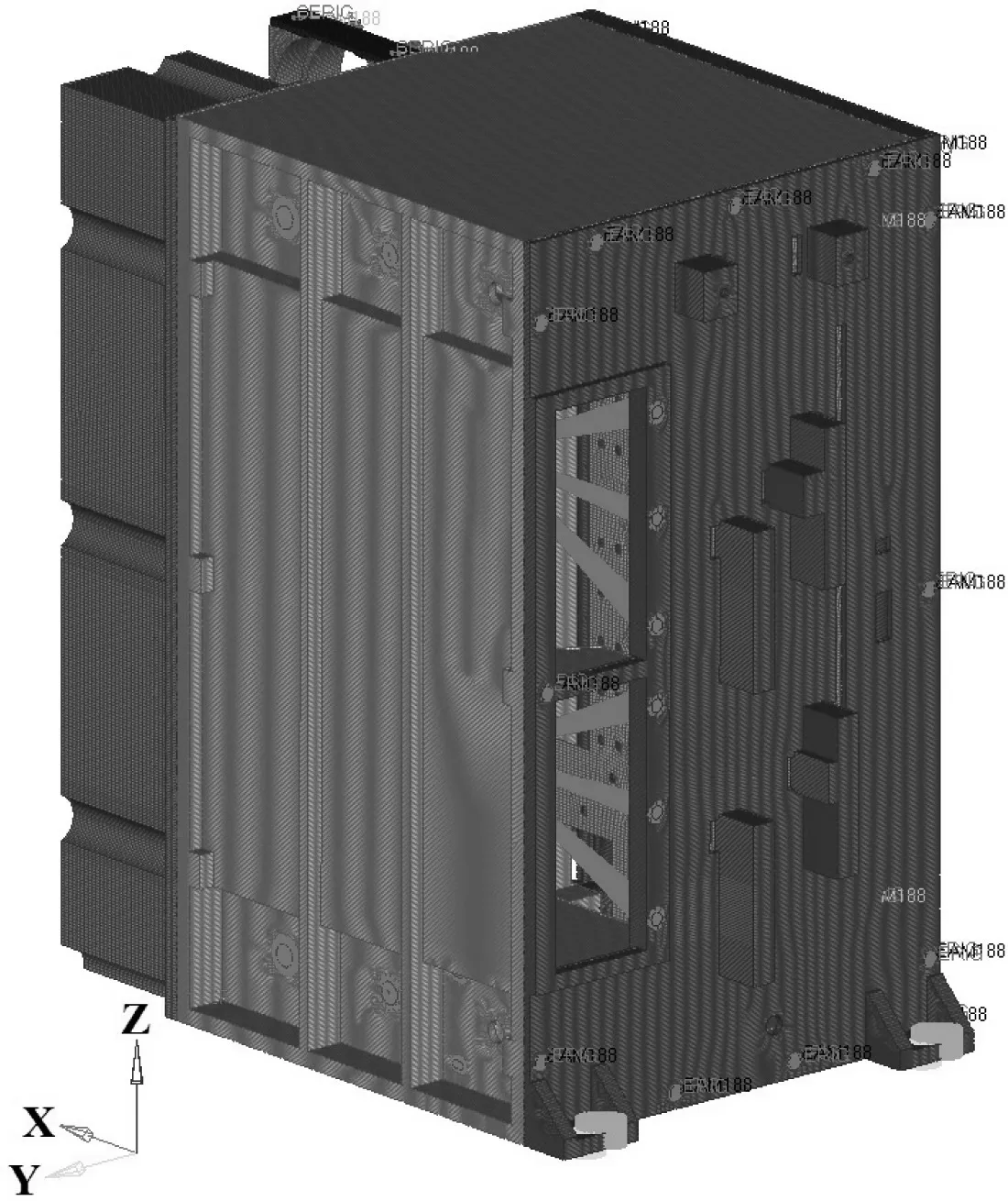
圖2 高壓變頻模塊有限元模型

在變頻器機組中，模塊前部通過螺栓連接將前面板兩個固定支座緊固約束于導軌，后部通過間隙配合的L形限位塊限制模塊的垂向位移，如圖3 所示。基于此，在模塊有限元模型中，前部的前面板固定支座的螺栓安裝孔處施加零位移約束，但后部不施加任何約束。原因一在于隨機振動分析是一種線性分析技術，無法同時分析間隙配合帶來的碰撞、接觸等非線性問題，二在于放開后部約束進行仿真分析，可以考核模塊在更危險條件下的抗振性能。

圖3 模塊在變頻器機組中的實際約束情況

模塊隨變頻器機組汽車運輸至安裝現(xiàn)場時，會相繼經(jīng)歷市區(qū)公路、高速公路、砂石路等多種運輸工況，本文選用最為嚴酷惡劣的砂石路運輸工況作為模塊隨機振動疲勞仿真分析和試驗考核的載荷輸入。將砂石路運輸工況歸納為圖4 所示的加速度功率譜密度（ASD）譜，可見該運輸工況的振動能量主要集中在前30 Hz 的低頻段。

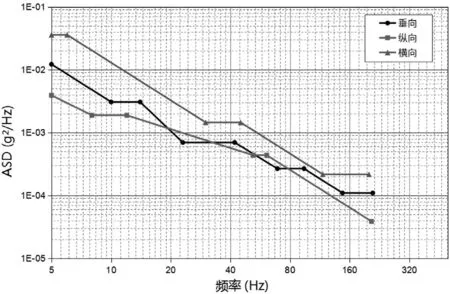
圖4 模塊隨機振動疲勞分析的載荷輸入ASD 譜

1.4 仿真結果分析

利用ANSYS 有限元軟件對模塊進行隨機振動仿真分析，圖5 所示為模塊在垂向、縱向和橫向三種隨機振動工況下的Von Mises 應力（即1σ 應力）云圖，可見模塊在三種載荷工況下的最大1σ 應力位置均位于前面板固定支座上方的螺栓安裝孔周圍。基于前述疲勞損傷評估方法，以砂石路最長運輸時間3 h 考核，計算得到模塊的疲勞累積損傷，如表2 所示。可見模塊在三種載荷工況下的疲勞累積損傷均小于1，總體疲勞累積損傷亦小于1，仿真結果說明模塊殼體結構滿足運輸振動的疲勞強度設計要求。

表2 模塊隨機振動疲勞仿真結果（模塊結構阻尼比為0.05）

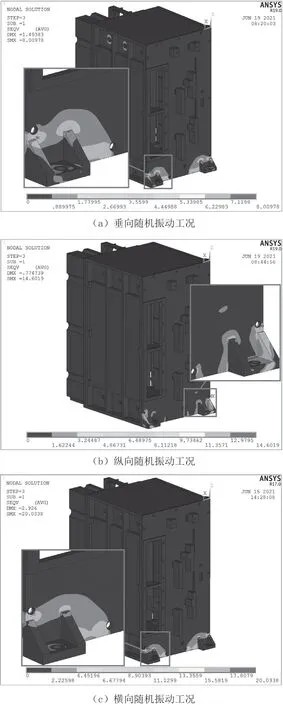
圖5 模塊的1σ 應力云圖（模塊結構阻尼比為0.05）

2 隨機振動疲勞試驗考核

2.1 試驗方案

為真實考核確定模塊的抗振性能是否滿足疲勞強度設計要求，同時也為驗證仿真分析模型，進一步修正確定該類SMC 模塊結構的阻尼比，本文基于圖4 的砂石路運輸工況ASD 譜依次開展模塊垂向、縱向和橫向的隨機振動疲勞試驗，模塊各方向均按砂石路最長運輸時間3h進行考核。

在模塊前面板、主箱體等關鍵部位共布置6 個加速度傳感器，包括2 個控制點和4 個監(jiān)測點，分別用于控制模塊的隨機振動載荷輸入和監(jiān)測模塊的隨機振動響應特性。基于以上試驗方案，在振動試驗臺上開展模塊模擬運輸隨機振動試驗，如圖6 所示。

圖6 模塊模擬運輸隨機振動試驗

2.2 試驗結果分析

隨機振動試驗過程中，通過肉眼觀察發(fā)現(xiàn)，垂向和縱向載荷工況下模塊無明顯晃動，橫向載荷工況下模塊后部上下晃動較為明顯。表3 所示為各加速度測點的隨機振動響應數(shù)據(jù)，可見垂向和縱向載荷工況的響應最大位置均為上外接銅排；橫向載荷工況的響應最大位置為主箱體頂面左后角，該處的加速度均方根值為1.215 g，相比輸入放大2.26 倍，在合理范圍以內(nèi)。各方向試驗完成后，經(jīng)仔細檢查確認，模塊殼體結構和電氣部件均無異常。

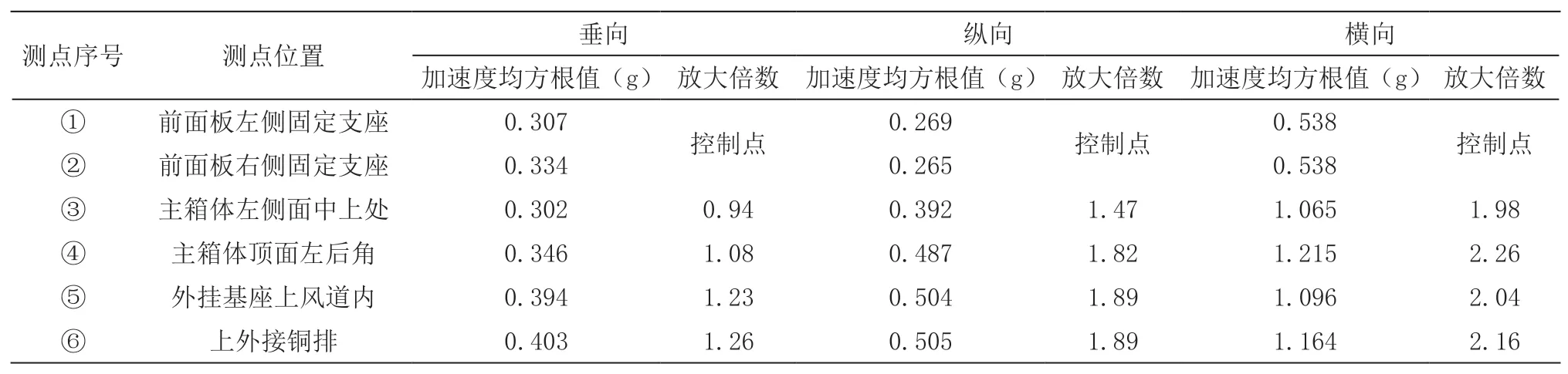
表3 各加速度測點隨機振動響應數(shù)據(jù)

3 仿真與試驗對標驗證

3.1 仿真結果與試驗結果對標

以試驗結果為參照，將各測點的ASD 響應譜作為衡量仿真結果準確程度的評價指標，同時也可作為確定模塊結構阻尼比的目標函數(shù)。由于模塊在縱向載荷工況下的隨機振動響應基本不受L 形限位塊是否安裝的影響，故取縱向載荷工況的仿真結果與試驗結果進行對標，以測點⑤——外掛基座上風道內(nèi)為例，圖7 所示為該測點的ASD 響應譜曲線對比圖。可見仿真結果與試驗結果整體趨勢一致，尤其是在5 ～50 Hz 的低頻段，曲線趨勢吻合程度尤為明顯；且仿真結果的1 階共振頻率為28.6 Hz，與試驗結果的26.8 Hz 僅相差6.7 %，這就證明了本文仿真分析模型的有效性和可靠性。

3.2 SMC 模塊結構阻尼比的確定

從圖7 可以看到，與試驗結果相比，仿真結果在1階共振頻率點的ASD 響應值偏大，這與仿真分析所取的模塊結構阻尼比偏小有關。通過不斷修正調(diào)整阻尼比的大小，迭代驗證仿真結果，最終使仿真結果在1 階共振頻率點的ASD 響應值與試驗結果的偏差處于一個相對合理的范圍，此時阻尼比大小為0.125。仍以縱向載荷工況的測點⑤——外掛基座上風道內(nèi)為例，圖8 所示為模塊結構阻尼比為0.125時，該測點的ASD響應譜曲線對比圖，表4 所示為該測點的各評價指標對標情況，可見1 階共振頻率、1 階共振峰值和加速度均方根值的相對誤差均在5.2 %以內(nèi)。

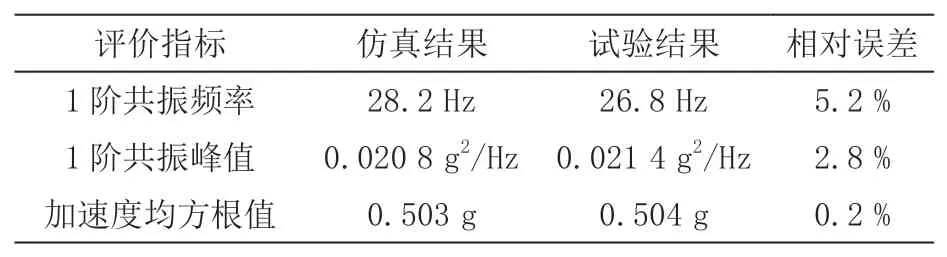
表4 各評價指標對標情況（模塊結構阻尼比為0.125）

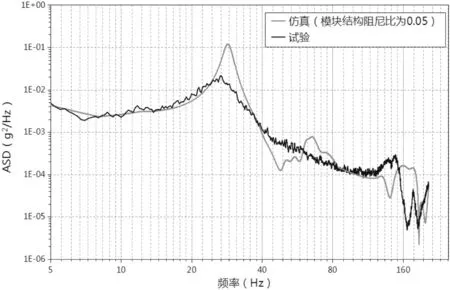
圖7 測點⑤的ASD響應譜曲線對比圖（模塊結構阻尼比為0.05）

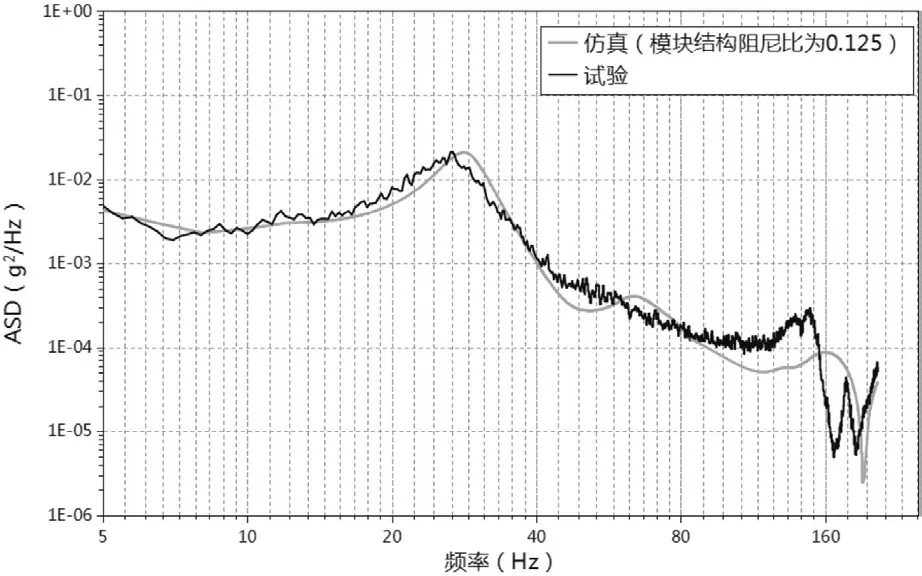
圖8 測點⑤的ASD 響應譜曲線對比圖（模塊結構阻尼比為0.125）

3.3 仿真結果更新

在確定模塊結構的準確阻尼比為0.125 后，需要重新計算并更新仿真結果。圖9 所示為模塊在垂向、縱向和橫向三種隨機振動工況下的1σ 應力云圖，可見模塊在三種載荷工況下的最大1σ 應力位置仍位于前面板固定支座上方的螺栓安裝孔周圍，只是最大1σ 應力相比前文有不同程度的降幅。更新模塊的疲勞累積損傷如表5 所示，可見模塊在三種載荷工況下的疲勞累積損傷均小于1，總體疲勞累積損傷亦小于1，仿真結果仍說明模塊殼體結構滿足運輸振動的疲勞強度設計要求。

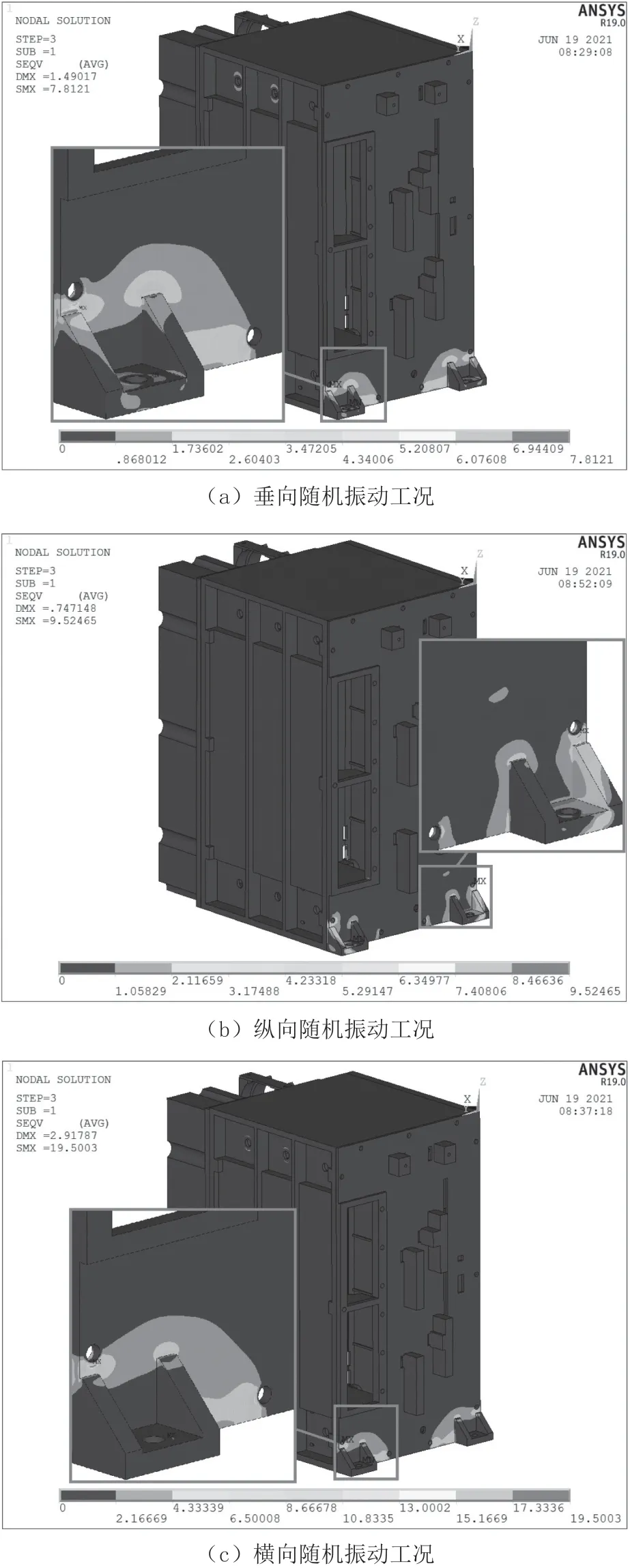
圖9 模塊的 應力云圖（模塊結構阻尼比為0.125）

表5 模塊隨機振動疲勞仿真結果（模塊結構阻尼比為0.125）

4 結論

本文針對SMC 高壓變頻模塊在實際運輸過程中的隨機振動工況，先后開展了模塊的隨機振動疲勞仿真分析和試驗考核，主要得到以下三個結論：

1）建立了預測模塊隨機振動響應及其疲勞損傷的仿真分析模型，將各測點的ASD 響應譜試驗值作為仿真結果對標指標，對比顯示仿真結果與試驗結果整體趨勢一致，驗證了仿真分析模型的有效性和可靠性。

2）通過仿真結果與試驗結果的迭代驗證，進一步修正確定了該類SMC 模塊結構的準確阻尼比為0.125；仿真和試驗結果都充分說明高阻尼系數(shù)的SMC 材料具有優(yōu)良的減振效果。

3）仿真和試驗結果均表明模塊在砂石路運輸工況下不會發(fā)生殼體的疲勞破壞以及電氣部件的損壞失靈，滿足運輸振動疲勞強度設計要求。