基于依賴最大化和稀疏回歸的多標簽特征選擇

吳喆君，黃 睿

(上海大學 通信與信息工程學院，上海 200444)

0 引 言

“維數災難”是多標簽學習面臨的挑戰之一[1-7]。通過特征選擇對高維數據進行維數約簡是克服該問題的有效手段[8-10]?；谙∈杌貧w的多標簽特征選擇算法利用優化得到的回歸矩陣進行特征選擇[11-14]。Ma等提出利用稀疏性來構建子空間(sub-feature uncovering with sparsity，SFUS)的多標簽特征選擇算法[12]，通過聯合稀疏特征選擇與多標簽學習來獲得特征的共享子空間。文獻[13]提出非負稀疏表示的多標簽特征選擇方法(multi-label feature selection based non-negative sparse representation，MNMFS)，融合了非負約束問題和l2,1范數最小優化問題。Zhang等提出一種基于流形正則化的多標簽特征選擇方法(manifold regularized discriminative feature selection for multi-label lear-ning，MDFS)[14]，將數據空間和標簽空間的流形正則化引入稀疏回歸模型。

當前，多數基于稀疏回歸的多標簽特征選擇算法認為數據的特征空間和標簽空間之間存在線性關系，在回歸模型中直接將數據從特征空間映射到標簽空間。然而大部分情況下兩者之間的線性關系并不成立。文獻[15]通過依賴最大化對多標簽數據進行特征提取。受此啟發，本文提出一種基于依賴最大化和稀疏回歸的多標簽特征選擇算法(multi-label feature selection with dependence maximization and sparse regression，DMSR)。該方法通過最大化投影子空間與標簽空間之間的依賴性來構建數據的低維空間，利用希爾伯特-施密特獨立性準則[15]來衡量兩者之間的依賴性，然后把該低維空間引入稀疏回歸模型中，將數據從特征空間映射到低維空間。相比于呈現稀疏性、二值性的標簽空間，該低維空間包含了更豐富的信息。結合l2,1正則化得到目標函數，利用交替優化的方式進行求解，得到用于特征選擇的回歸系數矩陣。

1 本文算法

1.1 目標函數

假設有多標簽數據集X=[x1,x2,…,xN]T∈RN×d，N是數據個數，d是特征個數，其中每個數據樣本為xi=[xi1,xi2,…,xid]， 標簽集合為L={l1,l2,…,lC}，C是總共的類別標簽個數，數據集對應的標簽為Y=[y1,y2,…,yN]T∈{0,1}N×C，xi的標簽為yi=[yi1,yi2,…,yiC]， 如果xi含有標簽lj，則yij=1， 否則yij=0。 令I表示單位矩陣，e表示全為1的向量。

所提算法DMSR源自稀疏回歸模型，使用最小平方損失作為損失函數的稀疏回歸模型的目標函數一般有如下形式

(1)

式(1)的目標函數直接將數據從原始特征空間映射到標簽空間，但是特征空間和標簽空間之間往往不存在線性關系，因此我們希望構建一個數據的m維子空間V=[v1,v2,…,vN]T∈RN×m， 把數據從原始特征空間映射到該低維子空間。受文獻[15]的啟發，DMSR最大化低維空間V和標簽空間Y之間的依賴性，使用希爾伯特-施密特獨立性準則(Hilbert-Schmidt independence criterion，HSIC)計算兩者之間的依賴性，其定義如下

HSIC(V,Y)=(N-1)-2Tr(HK1HK2)

(2)

(3)

同時，對低維空間V的每個維度之間進行正交約束，用V代替式(1)中的標簽空間Y， 再結合式(3)，則目標函數轉變為

(4)

其中，α和β為平衡參數。關于正則項R(W)， 這里采用l2,1正則化來保證稀疏性和減少離群點的影響[7,12]，即令R(W) 等于W的l2,1范數，從而得到最終的目標函數

(5)

1.2 優化求解

(6)

式(6)對W求導，并且令導數為零，可以得到

2XT(XW-V)+2βQW=0

(7)

解得

W=(XTX+βQ)-1XTV

(8)

把式(8)代入式(6)中的優化項，可以得到

(9)

其中，A=XTX+βQ， 從而得到如下只含有一個優化變量V的目標函數

(10)

該優化問題可以通過對矩陣I-αHYYTH-XA-1XT進行特征分解來進行求解，取前m個最小特征值對應的特征向量構成V。

算法1：DMSR算法

輸入：數據集X∈RN×d， 標簽Y∈{0,1}N×C， 平衡參數α，β， 低維空間的維數m。

輸出：特征排序。

(1) 初始化Q為單位矩陣Id×d；

(2) 迭代

(3) 求解式(10)得到V；

(4) 根據式(8)更新W；

(5) 根據W每一行的值更新Q；

(6) 直至收斂；

2 實 驗

本文將所提算法DMSR與其它4種多標簽特征選擇算法進行了比較，實驗結果表明所提算法能夠取得較好的性能。

2.1 實驗設置

為驗證所提算法性能，在Emotions、Birds、Enron、Image、Scene和Yeast等6個多標簽數據集上進行實驗。這些數據集都可以從互聯網上獲得，涵蓋了音頻、音樂、圖片、生物、文本等多種類型。表1列出了數據集的詳細信息，包括樣本數、特征數、標簽數、所屬領域以及URL鏈接。

表1 數據集信息

本文使用5種常用的評價指標來評估所提算法的性能，分別是漢明損失、排序損失、覆蓋率、1-錯誤率和平均精度[7,14]。假設T={(xi,yi)|1≤i≤p} 表示含有p個數據樣本的測試數據集以及其對應的標簽，某種算法對樣本xi的預測標簽為y′i，fk(xi)(1≤k≤C,1≤i≤p) 表示分類器輸出的樣本xi在第k個標簽上的分值，各評價指標的含義和定義如下：

漢明損失(Hamming loss，HL)：考察數據樣本被錯誤分類的情況，即分類器沒有預測相關的標簽或者預測了不相關的標簽

(11)

其中，Δ表示兩個集合之間的對稱差。

1-錯誤率(one-error，OE)：考察分類器輸出分值最高的標簽不屬于數據實際標簽的次數

(12)

覆蓋率(coverage，CV)：考察在分類器給出的標簽排序中，覆蓋樣本所有實際標簽所需的平均標簽個數

(13)

排序損失(ranking loss，RL)：考察出現排名顛倒的標簽對的情況，即不相關標簽的排名高于相關標簽的排名

(14)

平均精度(average precision，AP)：考察排名高于某個特定相關標簽的相關標簽的平均個數

(15)

這5種評價指標的取值范圍均為0到1，漢明損失、1-錯誤率、覆蓋率和排序損失取值越小，算法性能越好，平均精度則相反。

實驗采用如下4種多標簽特征選擇算法作為對比算法：

MDMR[8]：利用最大化依賴和最小化冗余(max-dependency and min-redundancy)實現多標簽特征選擇。

GMBA[9]：基于圖邊界的多標簽特征選擇算法(graph-margin based multi-label feature selection)，利用大邊界理論來衡量特征的重要程度。

SFUS[12]：通過聯合稀疏特征選擇與多標簽學習來獲得特征的共享子空間，并且將子空間引入稀疏回歸模型，完成特征選擇。

MDFS[14]：基于流形正則化的多標簽特征選擇算法，在優化模型中加入了數據空間和標簽空間的流形正則化項。

2.2 實驗結果與分析

圖1(a)～圖1(f)分別給出了在6個數據集上，不同算法的平均精度指標隨選擇特征個數改變的變化情況，其中，橫坐標軸表示選擇的特征個數，縱坐標軸表示平均精度。除了上述提到的4種對比算法，我們還采用了全特征進行實驗，將其結果作為比較基準，記為Baseline。從圖中可以看出，隨著選擇特征個數的增加，各個算法的性能先逐步提升，然后趨于平緩，一些算法的性能還出現了下降，而DMSR算法的性能超過了Baseline，這表明DMSR能夠選擇優秀的特征，提升分類器的性能。與其它對比算法相比，DMSR在大多數情況下表現出更優異的性能。在Emotions、Yeast和Image數據集上，選擇特征的個數變化時，DMSR的性能始終能夠高于其它算法，在Birds、Scene和Enron數據集上，雖然DMSR沒有在所有情況中均領先其它算法，但是其性能一直排名前3。

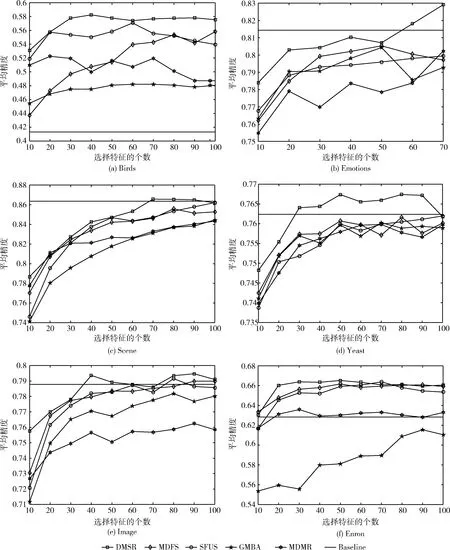
圖1 不同數據集上算法的性能

此外，為了對算法性能做進一步的定量分析，我們在每個數據集上利用各個算法選擇最重要的30個特征進行實驗。表2～表6列出了在5種評價指標上的實驗結果，各表中的最后一行“AvgRank”表示每個算法在不同數據集上的平均排名，不同算法中最優的結果加粗表示，↓表示評價指標越小，性能越好，↑表示評價指標越大，性能越好。從表中可以看出，由于實驗采用了5種評價指標和6種數據集，因此總共有30種比較情況，DMSR算法在其中的24種情況排名第一，6次排名第二，盡管在個別情況下DMSR的性能不如MDFS和SFUS，但整體上看DMSR仍然優于其它對比算法。綜合分析各個算法在5種評價指標上的平均排名，我們可以得到各個算法的性能排序：DMSR>MDFS>SFUS>MDMR>GMBA。DMSR、MDFS和SFUS都是基于稀疏回歸的多標簽特征選擇算法，而MDMR和GMBA是過濾式多標簽特征選擇算法，這驗證了利用稀疏回歸模型進行特征選擇的有效性。在大多數情況下DMSR的性能要優于MDFS和SFUS，這說明基于HSIC構建數據的低維空間并將其引入回歸模型，能夠選擇出更具有判別力的特征，從而有效提升多標簽分類器的性能。

表2 不同算法的漢明損失(↓)

表3 不同算法的排序損失(↓)

表4 不同算法的覆蓋率(↓)

表5 不同算法的1-錯誤率(↓)

表5(續)

表6 不同算法的平均精度(↑)

3 結束語

多標簽學習面臨“維數災難”的問題，利用稀疏回歸模型的多標簽特征選擇方法能夠有效去除冗余特征，提升算法性能，但是回歸模型中數據的特征空間和標簽空間之間通常不存在線性關系。本文提出一種基于依賴最大化和稀疏回歸的多標簽特征選擇算法DMSR，首先構建數據的低維空間，最大化低維空間和標簽空間之間的依賴性，該依賴性使用希爾伯特-施密特獨立性準則來衡量，然后將低維空間加入含有l2,1正則項的回歸模型，最后設計了一種交替優化的方法進行求解，利用得到的回歸系數矩陣選擇特征。在6個公共多標簽數據集上的特征選擇與分類實驗結果表明所提算法DMSR的性能優于其它對比算法。

DMSR算法沒有考慮標簽相關性，后續的研究工作將關注如何將標簽相關性引入回歸模型，從而進一步提高算法性能。