改進松鼠搜索算法的云計算多目標任務調度

陳孝如，曾碧卿

(1.廣州軟件學院 軟件工程系，廣東 廣州 510990；2.華南師范大學 軟件學院，廣東 佛山 528225)

0 引 言

近年來，為了滿足大規模應用程序的計算需求，云計算憑借其計算資源的高效性和靈活性得到了大規模部署[1]。云計算提供服務的主要形式有3種，分別為：基礎設施即服務(infrastructure as a service，IaaS)、平臺即服務(platform as a service，PaaS)以及軟件即服務(software as a service，SaaS)[2,3]。其中，IaaS可實現大規模應用程序部署，能夠提供靈活和可擴展計算資源的訪問[4]。然而，在IaaS云上高效且有效的執行大規模任務調度，仍然是一個亟待解決的問題[5]。

近年來，各種啟發式算法被用于求解任務調度問題，取得了一定的成效[6]。然而，面對大規模計算任務時，元啟發式算法的計算時間較長，由于局部搜索與全局搜索過早收斂和失衡的影響，可能會使算法陷入局部最優解。不同于傳統的元啟發式算法，松鼠搜索算法(squirrel search algorithm，SSA)[7]具有魯棒性和更快的收斂速度，在處理多目標約束優化問題的同時，可對復雜的多維搜索空間進行有效地優化。由于無需特定的算法參數，SSA已被用于解決任務調度、無線通信以及經濟調度等優化問題[8]。

基于上述分析，針對云計算中大規模應用程序的任務調度問題，提出一種改進SSA的云計算多目標任務調度方法，以對搜索空間進行有效的優化，合理調度多目標任務。所提方法的創新點總結如下：

(1)為了實現任務的高效調度，構建IaaS云模型，基于該模型設計多目標任務調度算法框架，并將成本和執行時間的最小化作為目標函數，從而有效地將用戶任務分配給各種可用的處理單元；

(2)由于傳統SSA存在容易陷入局部最優的問題，所提方法將入侵雜草優化算法(invasive weed optimization，IWO)的空間變異和擴散機制應用于SSA，并利用改進型SSA求解多目標優化問題，從而在最短時間內尋得最優調度方案。

1 相關研究

任務調度優化分為單目標優化和多目標優化。單目標優化方法只對完工時間或成本進行優化。然而，由于云計算的快速發展，需要考慮到多個服務質量(quality of service，QoS)目標，使得任務調度成為一個多目標優化問題[9]。由于用戶和提供者各自具有不同的優化目標，故多目標任務優化問題較為復雜[10]。就目前的研究現狀而言，針對云環境下的多目標任務調度優化問題的求解，主要采用的方法有啟發式算法、分層方法以及帕累托優化等[11,12]。

文獻[13]提出一種改進的非支配排序遺傳算法得出Pareto最優解集，并利用模糊優選法對該解集進行選優，確定了產品開發任務調度的最優執行方案。通過兩個經典多目標測試函數的求解及對比分析結果表明了改進算法的有效性和優越性。但在優化應用程序的執行時間、可靠性和負載平衡時未考慮計算資源的異構性。文獻[14]提出了一種蟻群算法的測試任務并行任務調度優化方法，對測試問題進行描述并與蟻群算法結合，設計了啟發函數、狀態轉移規則；通過依據算法流程來得到測試速度最快的任務調度序列；在任務序列多解的問題上，主要是通過提出資源均衡度的評價標準，得到最優的資源任務調度序列。然而，不同目標的結果取決于所分配權重的值，這些權重值也許不能充分代表用戶的決策。此外，該方法只產生不適合多目標決策問題的解決方案。

分層方法按順序優化任務調度目標，根據目標的重要性確定任務調度目標的優化次序，并根據目標的排序交替求解[15]。例如，文獻[16]提出一種基于蟻群算法的分層調度算法，將調度過程分為預分配、粗略調度和精細調度3個步驟，對目標函數進行順序優化。測試結果表明，使用這種新機制可以有效地減少計算時間。文獻[17]提出一種基于離散粒子群算法的靜態任務調度方法；求解過程中假定任務是非優先并且獨立的，使用負載平衡技術提高了方法的性能。然而，該方法時效性較差，優化過程需要多次迭代，尤其是當有多個目標約束時[18]。

為了克服聚合和分層方法的缺點，提出了基于帕累托的優化方法，以解決多目標任務調度問題。帕累托方法為優化問題的目標找到了幾個最優的折衷方案。使用帕累托支配的概念來為個體分配適應度。帕累托方法不需要將多個目標轉化為單目標公式，并在一個單一的過程中產生多個權衡解決方案。文獻[19]提出了工作流任務調度問題的多目標遺傳算法，在考慮任務優先級的同時還兼顧了云計算中的任務能耗。使任務的完工時間和成本達到最小化。采用遺傳算法解決了完工時間、成本和能耗之間的帕累托最優權衡問題，仿真結果表明了該方法的有效性。同樣，文獻[20]基于包括車輛云、路邊小云和集中式云三層體系結構，提出一種混合自適應粒子群優化(hybrid adaptive particle swarm optimization，HAPSO)算法資源分配和任務優化調度算法，可以有效地滿足來自道路用戶的大量任務請求，同時保持改進的服務質量。結果表明，對于多目標優化調度問題，HAPSO的收斂速度比標準粒子群優化和自適應粒子群優化更具優勢。然而，在帕累托任務調度方法中，由于帕累托優勢是一個偏序，很難為下一代選擇合適的個體。因此，如果選擇算子不能保持足夠的多樣性，所得到的解可能無法覆蓋整個帕累托前沿，則在開發多目標任務調度有效分配個體適應度的同時保持對整個優化方案的有效估計，仍是一個具有挑戰性的研究課題。

Jain M提出了SSA[21]，該算法模仿了飛松鼠的動態跳躍策略和特征，對于優化問題的最優搜索具有易于實現的優點，并且不易陷入局部最優。其數學模型主要包括食物和捕食者的位置，整個優化過程包括夏季和冬季兩個階段。然而，與其它智能進化算法相似，SSA也存在收斂精度低、收斂速度慢等缺點。根據SSA，全局搜索能力的單冬搜索方法不夠，使得算法容易陷入局部最優。此外，隨機夏季搜索方法降低了收斂速度，收斂精度也降低[22]。為了提高算法的收斂精度和收斂速度，提出了一種改進的松鼠搜索算法(improved squirrel search algorithm，ISSA)，包括跳躍搜索法和漸進搜索法。當松鼠與捕食者相遇時，將“逃逸”和“死亡”操作引入跳躍搜索方法，將“突變”操作引入漸進搜索方法。在優化過程中，ISSA還通過線性回歸選擇策略選擇合適的搜索方法。

2 系統模型與問題建模

2.1 IaaS云模型

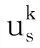
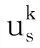
(1)

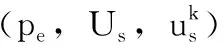
2.2 多目標調度的目標函數

(2)

只考慮一個實例序列和一個定價方案，其中實例序列類型是計算密集型的。則任務調度 (ET,C) 的目標函數為

minf=(ET,cost)e

(3)

2.3 調度算法框架

在整個調度過程中，如果計算資源(包括CPU和存儲系統)無法滿足用戶的任務需求，則可以通過任務管理器進行采集和處理任務數據。任務管理器具有接受和管理任務的功能，需要向調度器提供數據。任務管理器將通過成本、存儲和時間限制進行工作分配，并且通過全局資源管理系統對分配的資源進行了標記。整個調度算法是在云計算平臺中進行，兼容不同的物理服務器[23]。同時，可以訪問本地服務器資源管理(local server resource management，LRM)，每個LRM都支持許多虛擬機。IaaS云環境下的任務調度算法結構如圖1所示。

圖1 IaaS云環境下的任務調度

云計算系統由多個數據中心組成，這些數據中心可以通過使用來自世界各地的互聯網進行訪問，每個數據中心都有許多計算、存儲以及其它的資源。在每個服務器集群中，處理單元通過高帶寬連接網絡。在所提調度模型中，有效地將用戶任務分配給各種可用的處理單元，以優化用戶成本和時間。

3 改進型松鼠搜索算法

SSA是模擬飛行松鼠為躲避捕食者、尋找捕食的最佳地點以及以較小的代價進行捕食的滑翔行為。飛行松鼠的覓食策略靈活多變，這可以幫助飛行松鼠以最佳的方式應對食物資源。相比于其它搜索優化算法，SSA對搜索空間要求較少，且搜索效率較高，但在優化過程中也存在易陷入局部最優解，收斂速度較慢的問題。

3.1 松鼠搜索算法

松鼠是一種多樣的樹棲和夜間活動的嚙齒動物，其類似降落傘的薄膜特別適合滑翔。其滑翔搜索能力可以幫助其躲避捕食者、尋找捕食的最佳地點和以較小的代價進行捕食。松鼠可以通過展示動態覓食行為來優化食物資源的利用[24]。

在溫暖的秋天，由于橡樹籽數量多，且能夠滿足松鼠在秋天的營養需要，當它們發現橡樹籽后，會立即食用。在滿足了每天的能量需求后，開始尋找冬天的最佳食物來源；而在冬季，森林中樹葉的脫落增加了被捕食的風險，因此它們變得不活躍，但不冬眠。由于較低的溫度會導致更高的營養需求，儲存山核桃仁將有助于它們在極端天氣條件下維持能量需求，從而提高存活概率。因此，根據營養需要，有選擇地吃一些堅果，而將其它堅果儲存起來，這使得兩種堅果得到了充分利用。到冬季末，松鼠又活躍起來了開始覓食。如此循環往復，一直延續到松鼠生命的結束。在這個過程中，它們通過改變位置來探索不同的森林區域。SSA的尋優流程如圖2所示。

圖2 SSA的流程

為了簡化數學模型，需要考慮以下假設[25]：

(1)森林里有n只會飛的松鼠，假設樹上只有一只會飛的松鼠；

(2)每只松鼠都獨立地尋找食物，并通過表現出動態的覓食行為來優化現有食物資源的利用；

(3)在森林中，只有3種樹可供選擇，如普通樹、橡樹(橡樹籽的來源)和山核桃樹(山核桃仁的來源)；

(4)假設森林區域由k橡樹和一棵山核桃樹組成。

在SSA中，對于d維優化問題，每個松鼠的位置可以用一個d維向量來表示

Xi=[xi1,xi2,…,xij,…,xid],i=1,2,…,nxij=xmin+δ(0,1)·(xmax-xmin),j=1,2,…,d

(4)

式中：xmax和xmin分別是飛行松鼠位置的上下限，δ(0,1) 是[0,1]范圍內的均勻分布隨機數。

根據用戶定義的適應度函數，計算出每只飛鼠所在地的適應度值f(Xi)， 對應的值描述了可供搜索的食物源的質量，即最佳食物源(山核桃樹)、正常食物源(橡樹)和無食物源(普通樹)。

3.2 引入空間變異與擴散機制

SSA算法在優化過程中不可避免地陷入局部最優解，收斂速度較慢。因此，受IWO的啟發，將空間變異和擴散行為結合到SSA中，提出了一種ISSA。

第i只飛行的松鼠在一定范圍內選擇樹Ni上降落，以確保在該范圍內找到最佳食物來源，這個過程被稱為空間變異。Ni的個數由IWO算法中的生長和再生思想決定

(5)

式中：dmax和dmin分別是空間變化的最大和最小數量。f(·) 是適應度函數，fmax、fmin分別是f(·) 的最大值和最小值。

然后，由正態分布的空間擴散產生Ni隨機位置，平均值為第i只飛行松鼠的當前位置，標準差為σt， 其中σt的值根據迭代次數確定為

(6)

式中：σinitial為初始標準差，σfinal為最終標準差，t為當前迭代次數，tmax為最大迭代次數，n為非線性調和指數，常取3。

由上可知，空間擴散產生的新Ni位置可以表示為

(7)

式中：N(0,1) 是標準正態分布隨機數。

對隨機生成的Ni適應度函數值進行排序，選擇適應度函數值最小的位置作為第i只飛行松鼠的當前新位置。式(7)描述了ISSA的基本特征，即早期強調全局搜索，后期強調局部搜索。

ISSA的偽代碼如算法1所示。

算法1：ISSA的偽代碼。

Begin

定義輸入參數：εg是隨機滑行距離；R是[0,1]范圍內的隨機數；Gc是滑動常數，常取1.9；Pd為捕食者存在概率。

(1) 生成n只飛行松鼠的隨機位置：

Xi=[xi1,xi2,…,xid],i=1,2,…,n

(2) 評估每只飛行松鼠的位置是否適合。

(3) 通過空間變化和擴散進行重新定位：

(4) 根據它們的適應值， 按升序排列飛行松鼠的位置。

(5) 上報山核桃樹、 橡樹和普通樹上的飛行松鼠。

(6) 隨機選擇一些在正常樹上的飛行松鼠向山核桃樹移動， 其余的向橡樹移動。

(7) While 不滿足停止條件

(8) Fort=1 ton1(在橡樹上向山核桃樹飛去的松鼠總數)

(9) ifR1≥Pd

(12) end

(13) end

(14) Fort=1 ton2(在正常樹上向橡樹移動的飛行松鼠的總數)

(15) ifR2≥Pd

(18) end

(19) end

(20) Fort=1 ton3(在普通樹上向山核桃樹移動的飛行松鼠總數)

(21) ifR3≥Pd

(24) end

(25) end

(27) 使用更新季節常數Smin的最小值:

(28) 通過空間變化和擴散進行重新定位：

(29) 松鼠在山核桃樹上的位置是最終的最優解。

End

4 仿真及分析

4.1 仿真設置

CloudSim仿真工具包支持模擬云計算場景，支持大規模計算環境的建模和仿真，可為數據中心、物理主機、云服務代理和調度系統提供建模支持，因此，在IaaS云環境下使用CloudSim 3.0.3仿真工具包實現所提方法的調度方案。在實驗中，一個IaaS云提供商擁有一個數據中心、兩個主機和20個不同配置的虛擬機。數據中心和主機的配置見表1。虛擬機(virtual machine，VM)配置基于當前amazonec2產品，見表2，虛擬機的處理能力(即工作負載參數)見表3。

此外，ISSA算法的參數見表4。

4.2 性能指標

將完工時間、成本(財務成本)、超體積作為性能指標。ET是虛擬機最晚的完成時間，最小ET意味著用戶在執行任務時要付出適度的成本，因為云服務中用戶通常是按每小時的虛擬機使用量收費的。成本是從IaaS云提供商租賃VMs獲得的。

表1 IssA云環境的參數設置

表2 虛擬機的配置與類型

表3 工作負載參數

表4 ISSA算法的參數設置

ET也稱為總執行時間，是執行任務集合時使用的所有VMs最新完成時間，表示如下

(8)

成本是VMs成本與ET的乘積之和，四舍五入得最接近的整數表示為

(9)

超體積(hypervolume，HV)指標是通過計算得到非支配解決方案和參考點之間目標函數的空間體積，通過提供解集收斂性和多樣性之間的關系獲得的，是衡量多目標優化方法求解質量的一種綜合指標，計算如下

(10)

為了獲得HV值，每個方法在所有工作負載實例上獨立運行30次，并將每個算法獲得的30次運行的解合并成一個參考集，然后，在參考集上選取非支配解，形成帕累托前沿(pareto front，PF)，剔除由真PF支配的結果。將制造周期和成本標準化，使用參考點(1.1,1.1)計算HV值，該值越大，說明解決方案與參考點的相對空間體積越大，解的質量越高。

4.3 調度性能對比及分析

為了驗證所提方法在成本和時間方面的性能，將其與文獻[17]、文獻[19]和文獻[21]中的方法進行對比分析。其中文獻[17]提出一種基于PSO算法的靜態任務調度方法，求解過程中假定任務是非優先并且獨立的，使用負載平衡技術提高了方法的性能。文獻[19]采用遺傳算法(genetic algorithm，GA)算法解決了完工時間、成本和能耗之間的帕累托最優權衡問題，在考慮任務優先級的同時還兼顧了云計算中的任務能耗，使任務的完工時間和成本達到最小化。文獻[21]提出了SSA算法，模仿了飛松鼠的動態跳躍策略和特征，對于優化問題的最優搜索具有易于實現的優點。

為了確保不同方法之間的公平比較，工作負載實例的初始生態系統(總體)、生成數、停止條件和硬件資源都是相同的。并且NASA Ames iPSC/860是一些標準格式的工作負載，用于評估分布式系統的性能，而Uniform是合成工作負載。

4.3.1 不同并行任務種類下的執行時間和成本

對于所有測試的工作負載實例，將所提方法獲得最佳結果所耗費的執行時間(以秒為單位)與文獻[17]、文獻[19]和文獻[21]進行比較，結果如圖3所示。

圖3 執行時間的對比結果

從圖3可以看出，對于所有測試的工作負載實例，所提方法的執行時間均少于其它對比方法。所提方法利用改進ISSA能夠在較短的計算時間內獲得更高質量的解決方案，優于文獻[21]中傳統的SSA。文獻[17]和文獻[19]分別使用GA和PSO算法，雖能夠在一定程度上縮短執行時間，但隨著任務數量的增加，算法處理效率不高，導致執行時間較長。由此可驗證所提方法是求解多目標任務調度優化問題的有效方法。

此外，由5000個大小的工作負載實例的非支配解決方案如圖4所示。

由圖4可知，無論在NASA標準或是Uniform標準下，所提方法的性能明顯優于其它對比方法。如圖4(a)所示，在NASA標準下，所提方法的顯著性能歸功于其底層SSA算法的全局收斂性，并且引入空間變異與擴散機制，從而使其能夠獲得更好的收斂性，有效地處理大的搜索空間，因此，其對于成本的控制優于其它文獻所提方法；其中，文獻[17]所提方法由于缺乏全局搜索能力，因此其性能相對較差；而文獻[21]和文獻[19]所提方法則處于中等水平。在Uniform標準下，如圖4(b)所示，文獻[17]的GA和文獻[19]的PSO算法在處理多目標調度問題，處理效率一般，且全局收斂性有待提高；文獻[21]方法與所提方法性能較為接近，但所提方法憑借其變異與擴散機制帶來的更好的收斂性，具有更好的性能，因此略優于文獻[21]所提方法。

4.3.2 不同任務數量下的HV指標提升

對于不同任務數量，幾種方法在HV指標方面的對比結果見表5。

從表5中可以看出，對于所有工作負載實例，相比文獻[17]、文獻[19]和文獻[21]提出的方法，所提方法的HV值有顯著提高。在不同的工作負載下，所提方法的HV值比文獻[21]的SSA算法提高了16.32%～35.51%，而相比文獻[19]的PSO算法性能提升了37.75%～63.89%，與文獻[17]中的GA相比，提高了94.40%～120.24%。由此可見，所提方法具有較好的收斂性和解決方案的多樣性，從而得到全局最優解決方案，完成多目標任務調度，實現成本和執行時間最小化。

圖4 非支配解決方案的對比

表5 不同任務數量的HV指標對比結果

5 結束語

針對云環境中多目標任務調度優化所存在的收斂慢且易陷入局部最優的問題，提出一種改進SSA的云計算多目標任務調度方法。基于IaaS云模型，設計了多目標任務調度算法框架，并且將成本和執行時間的最小化作為目標函數，利用ISSA進行問題求解，其中引入空間變異與擴散機制改進傳統的SSA。此外，在CloudSim模擬器工具包中，使用NASA標準工作負載和Uniform合成工作負載對所提方法進行實驗驗證，結果表明，所提方法的成本、執行時間和HV均少于其它對比方法，以NASA為例，當任務數量為5000時，其執行時間和HV分別是32.12 s和21.50，并且當執行時間達到2500 s時，所提方法快速收斂，且成本僅約為10元。

所提方法具有較大的服務質量提升空間，可以對其進行擴展，以處理對可靠性和安全性需求較高的大型負載實例。此外，實驗僅考慮了NASA和Uniform兩種工作實例，后續工作中將考慮更多實例類型，以提高所提方法的普適性。