指數平滑與自回歸融合預測模型及實證

包研科，陳 然，鄭宏杰，馮永安，王 江

1.遼寧工程技術大學 理學院，遼寧 阜新 123000

2.遼寧工程技術大學 智能工程與數學研究院，遼寧 阜新 123000

3.北京泛鵬天地科技股份有限公司，北京 100000

4.遼寧工程技術大學 軟件學院，遼寧 葫蘆島 125000

對事物本質的洞察和演化狀態的前瞻是正確決策和有效控制的必要條件。隨著大數據和人工智能時代的到來，在預測、決策以及系統控制領域，對系統動態指標的在線監控和預測工具的需求持續增加。

對預測理論和技術的研究可以追溯到20世紀初。1927年，數學家Yule為了預測市場變化的規律，提出自回歸（autoregressive）模型，標志著時間序列分析方法的產生[1]。至今九十多年的時間，經典的時間序列分析理論與方法已經發展成為一種非常嚴謹的理論與技術體系。經典的理論可以劃分為X-11技術體系和Box-Jenkins方法體系。

1954年，美國普查局的Shiskin首先開發了X-1方法，開始大規模地對經濟時間序列進行季節調整[2]。此后，季節調整方法不斷改進。1965年發表了X-11方法，該方法基于多次迭代的移動平均法進行成分分解，剔除波動性的影響[2]。X-12方法是在X-11方法的基礎上發展而來的，也是基于移動平均法的季節調整方法。X-12方法對X-11方法進行了以下改進[3]：（1）擴展了對貿易日和節假日影響的調節；（2）提出了基于偽加法模型和對數加法模型的季節、趨勢循環和不規則要素的分解方法；（3）增加了對季節調整結果穩定性的診斷。20世紀70年代，美國學者Box和英國統計學者Jenkins提出了一整套關于時間序列分析、預測和控制的方法，被稱為Box-Jenkins方法，也被稱為ARIMA（autoregressive integrated moving average）模型[4-5]。Box-Jenkins方法基于差分技術，剔除趨勢特征，再對時間序列進行建模及預測，廣泛應用于金融時間序列預測問題[6-7]。1998年，美國普查局季節調整首席研究員David Findley提出X-12-ARIMA方法[8]。X-12-ARIMA方法能夠對數據做更加豐富的預處理，檢測和修正不同類型的離群值，估計并消除日歷因素的影響，對季節調整的效果進行更嚴格的診斷檢驗[2]。

近三十年，隨著數據科學的發展，特別是人工智能的發展，演化出了基于人工神經網絡[9]（ANN）技術和深度學習（DL）的新型預測技術，機器學習（ML）在預測領域得到廣泛應用。其中，源于自然語言處理（NLP）領域的循環神經網絡[10]（RNN）、長短期記憶（LSTM）循環神經網絡[11]、門控循環單元（GRU）網絡[12]和脈沖神經網絡[13]（SNN）等模型被研究人員引入到時間序列預測應用中，借鑒、改進、融合，服務于管理決策和控制。廖大強等[14]提出多分支遞歸神經網絡學習算法，通過改進一般的BPTT學習算法，對混沌時間序列進行預測。古勇等[15]探討了循環神經網絡在非線性動態過程建模和控制中的應用，提出兩步LM算法訓練循環神經網絡模型，研究了基于該模型的擴展DMC預測控制策略，結果表明控制器的性能得到了很大提高。Ma等[16]考慮時空相關性，提出了一種限制玻爾茲曼機（RBM）與RNN相融合的預測模型，對交通擁堵演變進行建模和預測，在不到6分鐘的時間內，預測精度可以達到88%。Zhang等[17]提出一種基于RNN和典型模式發現（RPD）相融合的金融預測策略，對標準普爾500指數（S&P 500 Index）進行預測，結果表明該方法在RNN的基礎上最多可提高6%的預測精度，但要以較高的均方誤差為代價。王鑫等[18]提出一種基于LSTM的故障時間序列預測方法。黃婷婷等[19]針對金融時間序列預測的復雜性和長期依賴性，提出一種基于深度學習的LSTM網絡金融時間序列預測模型。文獻[16]雖考慮了時空相關性，但由于梯度消失和梯度爆炸問題的存在，無法處理展開過長的時間序列；羅向龍等[20]針對這一問題提出一種基于K-最近鄰（KNN）與LSTM網絡相融合的短時交通流預測模型，預測性能得到一定的改善。Liu等[21]提出基于LSTM的銀行網點存款準備金預測方法，并成功地將預測系統部署到測試環境中。

GRU模型是LSTM模型簡化變體。文獻研究表明[22-23]，GRU具有與LSTM類似的性能，但計算速度比LSTM更快。張金磊等[24]提出基于差分運算與GRU神經網絡相結合的金融時間序列預測模型，對標準普爾500股票指數進行預測，結果表明該方法能夠實現比傳統方法（如ARIMA模型）更好的性能，并且具有相對較低的計算開銷。Xiuyun等[25]提出一種基于GRU的短期負荷預測模型，在黑龍江省某地區的電力負荷數據上具有較好的預測效果。Hossain等[26]提出一種LSTM和GRU的組合預測模型，實驗表明其預測性能優于以往所有的神經網絡方法。Jia等[27]提出基于GRU的礦井瓦斯濃度預測模型，隨著數據量的增加，與SVR、BPNN、RNN和LSTM模型相比，該模型的時間復雜度更低。

SNN網絡以更接近人類神經元工作機理的方式運行，被稱為第三代神經網絡，往往表現出更好的網絡性能[28]。陳通等[29]提出一種基于SNN的光伏系統發電功率預測模型，相對于BP-ANN和SVM預測模型具有更高的預測精度和適用性。

本文的選題，源自北京泛鵬天地科技股份有限公司銀行管理會計咨詢業務中提出的隔夜頭寸預測問題，研究工作始于2019年初。隔夜頭寸預測屬于金融時間序列一步預測問題，其中各類存款日余額是主要的觀測變量。從理論的成熟度講，馬爾科夫鏈模型應為首選，或者可以選擇AR(1)、ARMA(1,k)模型和指數平滑模型。然而，此類模型的應用，一是需要觀測變量的大量歷史數據支撐，二是依賴觀測變量的齊次性或平穩性。由于商業銀行業務數據的敏感性，本文的研究工作無法對觀測變量的演化特征進行直接的觀測和分析，難以直接應用成熟模型及其建模技術。因此，研究團隊提出了建立融合指數平滑與自回歸模型預測原理的輕啟動預測模型的思想路線。所謂“輕啟動預測”，指在時間序列預測問題中，不需要對大量的歷史數據進行觀察和分析、提取時間序列的結構因素和特征，也不需要大量的離線或在線數據對算法進行訓練，僅以系統能量變化對序列演化特征的基本影響為先驗假設建立一步預測模型，在少量必要的數據支撐下即可啟動預測，然后借助滑動窗口技術，實現模型長期在線工作并保持預測的有效性。本文的主要工作包括：提出了EABPs模型并討論其預測機理，實證分析模型最優啟動參數問題，分析了模型預測誤差的性質以及序列的波動特征同預測有效性的關系，分析了數據降噪對模型預測性能的影響。

1 EABPs模型

任何系統的發展與波動是系統能量變化的表現。時間序列是一個單變量廣義能量系統，預測的不確定性源自外部因素的干擾，表現為系統模型不能恰當地解釋系統的所有變化；系統內部的能量變化引起的系統震蕩同外部擾動因素造成的不確定性是動態平衡的。基于這樣的思想認知，以及參考借鑒混沌時間序列預測的思想原理和技術方法[30]，本文提出了輕啟動預測模型。

設x為系統的某個總量指標，假定x(t)是一個二階矩過程，且至少存在二階記憶。

所謂對x(t)的一步預測，即以t時刻為預測原點，估計t+1時刻的指標狀態，記后驗預報誤差。

假定Δt=(t+1)-t是一個“小的”單位時間，容易理解，從t到t+1時刻趨勢性和周期性因素對x(t)狀態變化的解釋能力是有限的。因此，對t+1時刻的系統狀態進行估計，可以僅考慮t時刻的系統能量變化率和系統發展速率兩個因素。本文的觀點是：后驗預報誤差ε(t+1)同t時刻的系統能量變化率正相關，與系統發展速率負相關，即系統因能量的漲跌引發的不確定性受系統演化趨勢的抑制。于是，對二階記憶過程x(t)進行一步預測的微分動力學方程為：

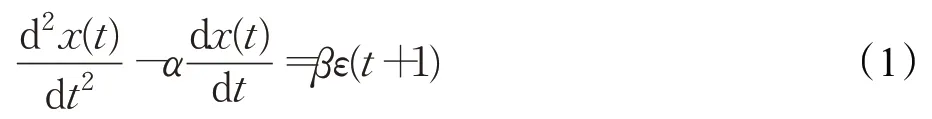
其中，α為系統負阻尼系數，β為系統平衡系數，α＞0,β＞0。

定理微分動力學方程（1）等價于一類無隱層BP神經網絡。

證明對微分動力學方程：

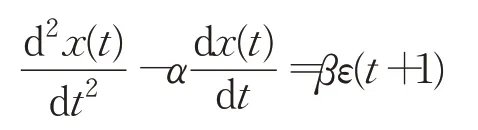
進行有限差分離散化，有：

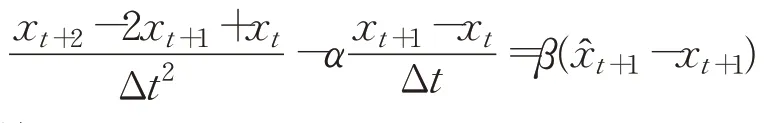
整理得：

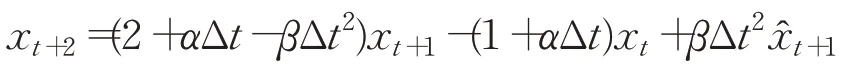
記：

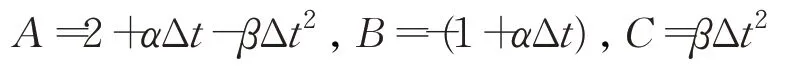
于是，得到遞推方程：

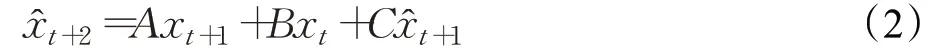
令：

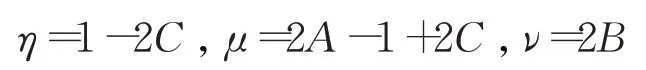
表明遞推方程（2）是指數平滑（ES）模型：

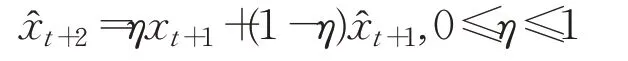
和自回歸（AR）模型：

的疊加模型，揭示了微分動力學方程（1）的預測機理。

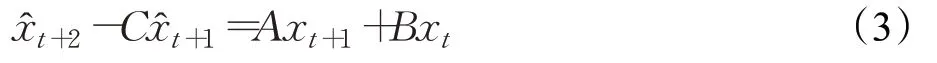
令：

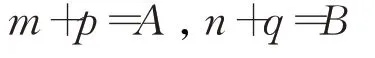
則方程（3）等價于方程組：

即：

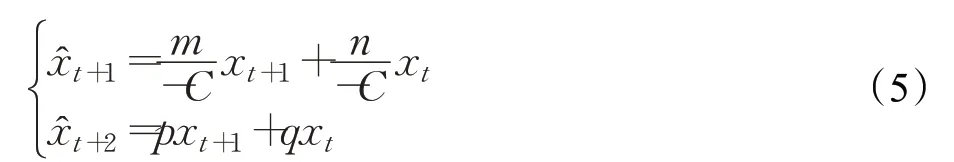
其矩陣形式為：

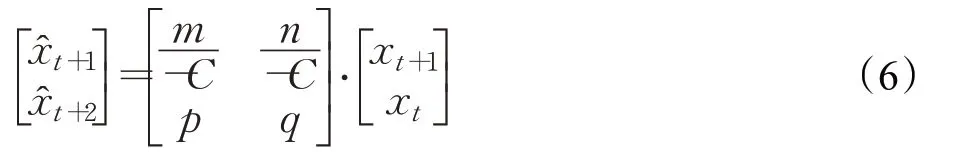
顯然，方程組（6）可表示為一個無隱層BP神經網絡：

其中，向量：

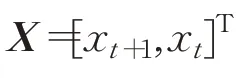
和

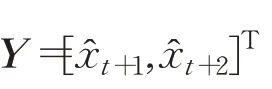
分別為網絡輸入和輸出，b=[b1,b2]T為閾值向量，矩陣：

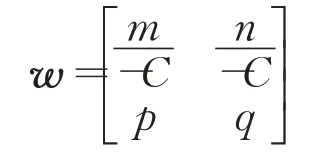
為權值矩陣，f為非線性激活函數。定理得證。

定理的證明過程描述了微分動力學方程（1）同ES模型和AR模型的聯系，以及BP神經網絡表達和預測應用方法。為后文敘述簡便，稱由微分動力學方程（1）定義的一步預測模型為EABPs模型（ES和AR模型的融合與BP網絡實現），其網絡單元結構如圖1。

由此可知，本文提出的EABPs模型自身的特點由指數平滑、自回歸和BP神經網絡模型三者共同決定。

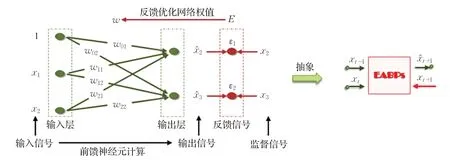
圖1 EABPs模型的網絡單元結構Fig.1 Network unit structure of EABPs model

圖2 EABPs模型的循環預測機理Fig.2 Cycle prediction mechanism of EABPs model

（1）基于指數平滑模型的預測，理論上是對均值趨勢的預測。即在：

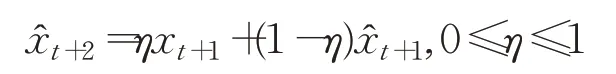
中，通常遵循新值優先的原則[31]，即xt是的最有可能的近似值。顯然，指數平滑模型對序列從t到t+1的狀態變化不敏感。

（2）自回歸模型的參數估計遵循最小二乘規則，因此，基于xt和xt+1預測xt+2時，的期望值在xt與xt+1所確定的直線上：

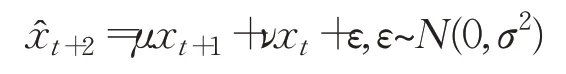
顯然，自回歸模型對序列從t到t+1的狀態變化較敏感。

因此，融合指數平滑模型和自回歸模型的預測結果是合理的。在一般情況下，較二者更接近t+2時刻的實際發生值。

（3）前文已經證明了方程（1）同無隱層的BP神經網絡等價，則依賴BP算法的自適應性確定融合模型參數，在一定程度上可以平滑模型預報值的過敏反應。

2 EABPs-RNN過程

在應用中，EABPs模型遞歸使用，形成類似于RNN的結構，如圖2。

由圖2可知，獲得EABPs模型的一個后驗預報誤差ε需要指標x的3個歷史數據，由此構成了模型觀測的最小時序窗口，記為e。

由BP算法基于累積誤差的“誤差反向傳遞權值修正”原理，可知EABPs-RNN過程的實現需要確定更新權值的時序窗口。因此，設定該時序窗口為由窗口e以單位時間步長連續滑動形成，記為M，如圖3。不妨仍以M表示這個窗口的寬度，稱為EABPs模型的啟動參數。顯然，3≤M＜∞。則模型訓練次數為M-e+1，即窗口e的滑動次數。

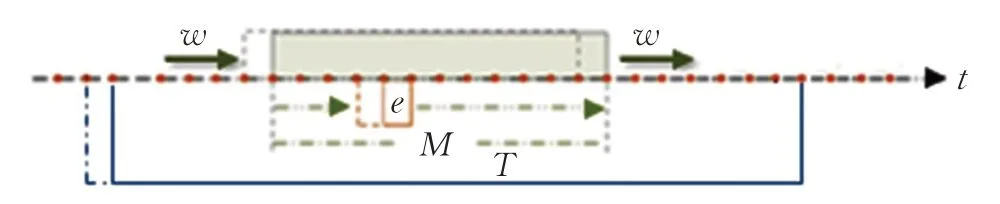
圖3 EABPs-RNN過程的計算窗口Fig.3 Calculation window of EABPs-RNN process

2.1 模型訓練

下面給出在窗口M上進行模型訓練、更新權值矩陣和閾值矩陣的具體計算過程。

步驟1數據預處理

假定以時間t為預測原點，則窗口M中的初始數據向量為：

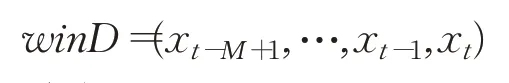
首先，采用min-max歸一化對窗口數據wi nD進行處理，以消除不同窗口數據的量級差異。轉換公式如下：

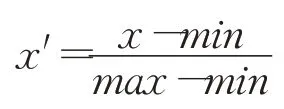
其中，min為窗口數據winD中的最小值，max為窗口數據winD中的最大值。x為原始窗口數據，x′為歸一化后窗口M中的數據。

其次，對歸一化后的數據進行格式化變換，構造出輸入矩陣：

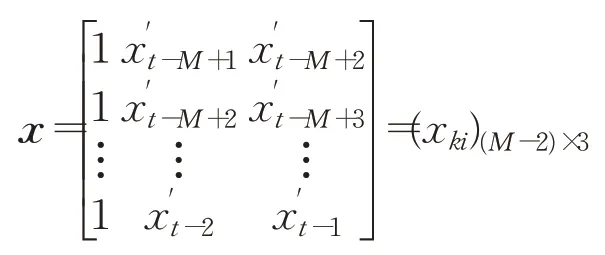
和監督矩陣：

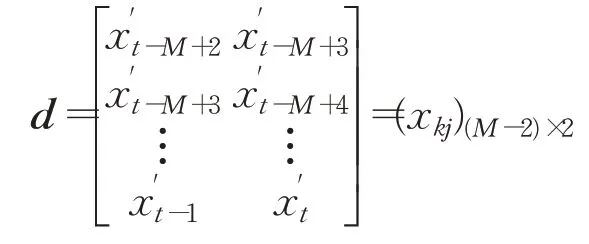
其中，k=1,2,…,M-2表示權值修正需要的最低訓練次數；i=0,1,2代表輸入節點編號，i=0時代表偏置項1；j=1,2代表輸出節點編號。

步驟2正向傳遞

輸出層中第j個節點的輸入表達式為：

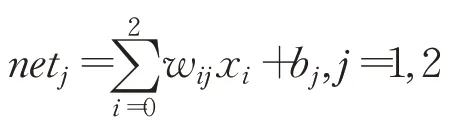
輸出層中第j個節點的輸出表達式為：

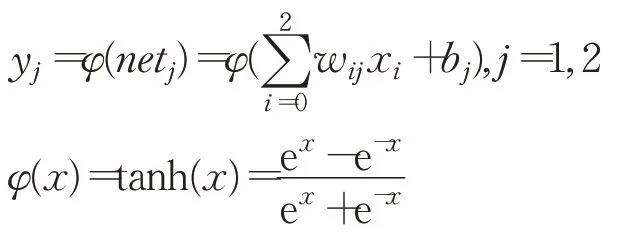
步驟3計算累積誤差

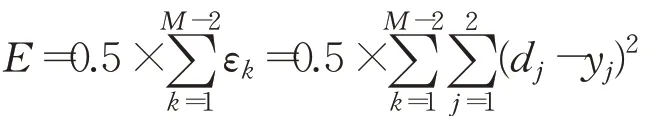
步驟4誤差反向傳遞

權值修正表達式為：

閾值修正表達式：

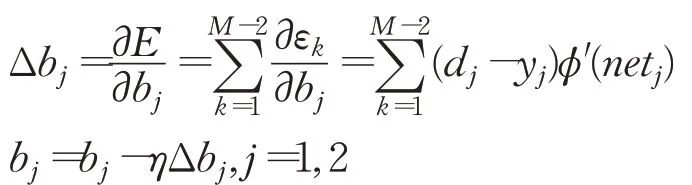
其中，η為最優學習速率。

當累積誤差E＜eps（閾值）或達到最大學習次數epoches，則可終止訓練。如不滿足終止條件，則繼續進行模型訓練。

2.2 預測過程

訓練終止后，提取窗口M中的最后兩個數據和，進行窗口M上的一步預測。具體計算過程如下：

步驟1輸入數據：

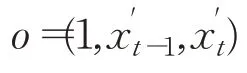
步驟2正向傳遞。

輸出層的輸入表達式為：

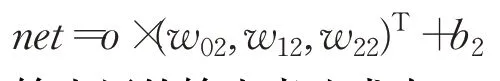
輸出層的輸出表達式為：

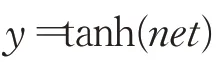
這時，y即為的預測值，又記為。

步驟3由于網絡訓練時對原始數據進行了歸一化處理，因此，需要對進行逆歸一化：

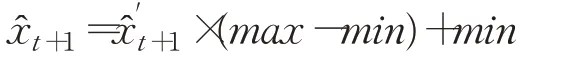
待到第一輪模型訓練和預測完成后，將窗口M向前滑動一步，即在窗口M中，淘汰舊數據xt-M+1，添加新數據xt+1，此時窗口數據向量變為：

2.3 模型復雜度

網絡模型的復雜度分析包括時間復雜度和空間復雜度。時間復雜度即模型的運算次數，可用FLOPs衡量；空間復雜度即模型的參數數量。

本文模型的創新之處在于，時序長度大于等于M時，便可滾動進行模型訓練和預測過程，因此對模型復雜度的分析皆以一個時序窗口為單位進行。

假定網絡輸入神經元數為Cin，輸出神經元數為Cout，下面給出本文模型的時間復雜度和空間復雜度。

（1）時間復雜度

①模型訓練

本文討論的時間復雜度為最壞情況下的時間復雜度，則模型訓練的終止條件為達到最大學習次數epoches。故模型訓練過程的

又因為輸入和輸出維數是固定的，Cin=3、Cout=2，則：

即模型訓練過程的時間復雜度為：

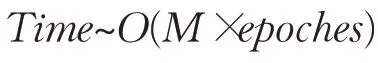
②預測過程

正向傳遞FLOPs1=2×Cin

激活函數FLOPs2=5

故預測過程的

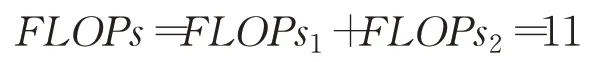
即預測過程的時間復雜度為：

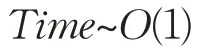
（2）空間復雜度

空間復雜度就是神經網絡中待優化參數的個數，即所有的權值w和所有的閾值b的總和。故本文模型的總參數為：

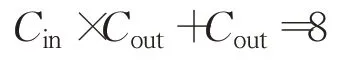
即本文模型的空間復雜度為：

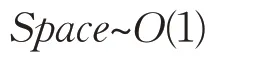
2.4 模型有效性評價

模型有效性評價是機器學習算法研究和應用的重要內容。

本文定義模型有效性評價窗口由窗口M滑動T次形成，不妨記為T，如圖3。于是，窗口T的寬度為T+1。在窗口T上，取前T個預測值和與之對應的真實值對預測效果進行評價，然后將窗口T向前滑動一步，用新窗口數據重復進行模型預測效果的評價。

本文主要由預報誤差和預報同態性兩類指標對模型有效性進行評價。

（1）預報誤差本文研究使用平均絕對百分比誤差（mean absolute percent error，MAPE），定義為：

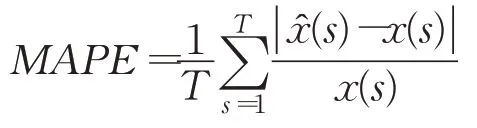
MAPE值越小，模型預報越準確。

在同文獻[24]的GRU模型進行比較分析時使用均方根誤差（root mean squared error，RMSE），定義為：

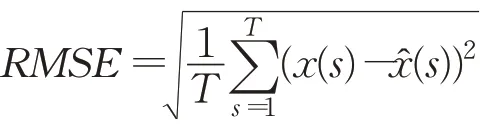
RMSE值越小，模型預報越準確。

（2）預報同態性模型預報的同態度（homomorphism rate，HR）定義為模型預報值的環比指數特征與變量觀測值環比指數特征之間相似性的度量：

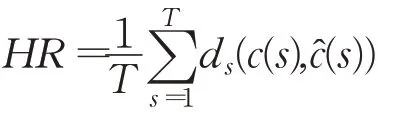
描述預測模型對變量波動態勢的跟蹤能力，其中：

顯然，0≤HR≤1。同時，HR值越大，模型對變量波動態勢的跟蹤能力越強。

模型預報的同態度在有些文獻[9]中稱為命中率（hit rate，HR）。

3 實證分析

3.1 數據說明

按照時間序列數據的環比中位數大于、等于和小于1，選取了12個樣本，用于對本文模型進行實證分析，見表1。

實證分析采用MATLAB自定義程序。

EABPs模型的優化學習速率在0.01～1之間按“預測誤差最小”準則實驗確定；最大訓練次數epoches=5 000，誤差閾值eps=6E-10。

3.2 啟動參數對預報有效性的影響

EABPs模型的啟動參數是“輕啟動”的關鍵指標。

本節考察啟動參數M對EABPs-RNN過程預報有效性的影響。實驗將M設定為從3到10的八種不同取值，對每一樣本根據“預測誤差最小”準則確定優化學習速率后，評價模型的預報誤差和同態度。同時，基于實驗結果給出EABPs模型最優啟動參數的參考值。

限于篇幅，僅報告12個樣本的中位誤差和中位同態度，計算結果見表2。

由表2可知，啟動參數M=e=3時，中位誤差最小，中位同態度接近最大。

為使觀察更加直觀，繪制了表2中計算結果的Box圖，如圖4和圖5。

表1 樣本數據描述Table 1 Sample data description

表2 啟動參數對模型有效性的影響Table 2 Influence of starting parameters on model validity

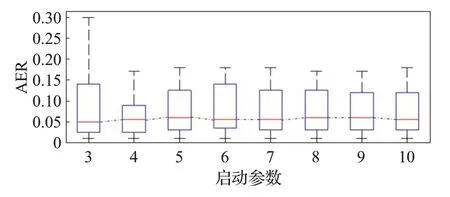
圖4 啟動參數對預報誤差的影響Fig.4 Influence of starting parameters on prediction error

圖4表明，啟動參數M≥4時，預報誤差的變化不大。

圖5表明，啟動參數M=6是預報同態度變化特征的一個分界點；M≤6時同態度較高，M＞6同態度明顯降低。

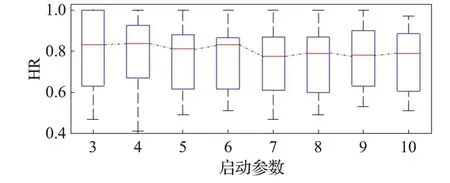
圖5 啟動參數對預報同態度的影響Fig.5 Influence of starting parameters on homomorphism rate of forecast

綜合圖4和圖5的信息，從模型穩健性的角度看，M=6是最優啟動參數的參考值；從本文“輕啟動”的預測思想來看，最優啟動參數也可選為M=3。

基于上述結果，本文的討論將在M=3的條件下進行。對表1中12組數據進行預測，其預測結果見圖6～17，并通過絕對預報偏差的卡方擬合優度檢驗結果，分析了EABPs-RNN過程預報誤差的性質。

設絕對偏差數據X的概率分布函數為FX(x)，本文假定先驗分布為指數分布，則：其中參數θ未知。

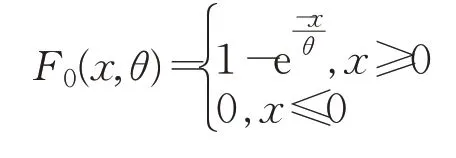
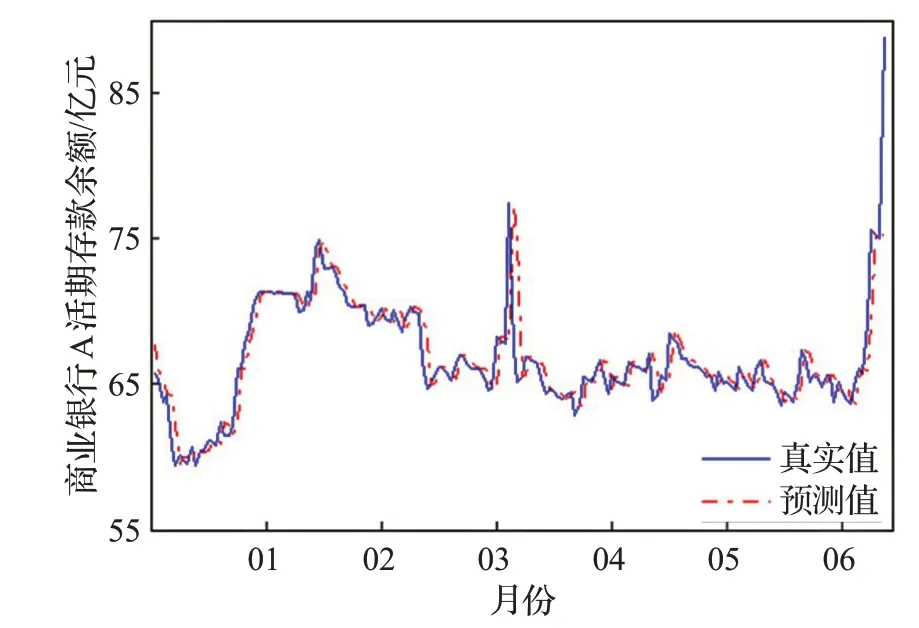
圖6 商業銀行A活期存款余額數據預測結果Fig.6 Forecast results of current deposit balance data of com-mercial bank A

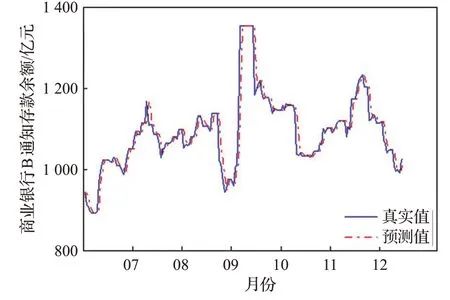
圖7 商業銀行B通知存款余額數據預測結果Fig.7 Forecast results of call deposit balance data of commercial bank B

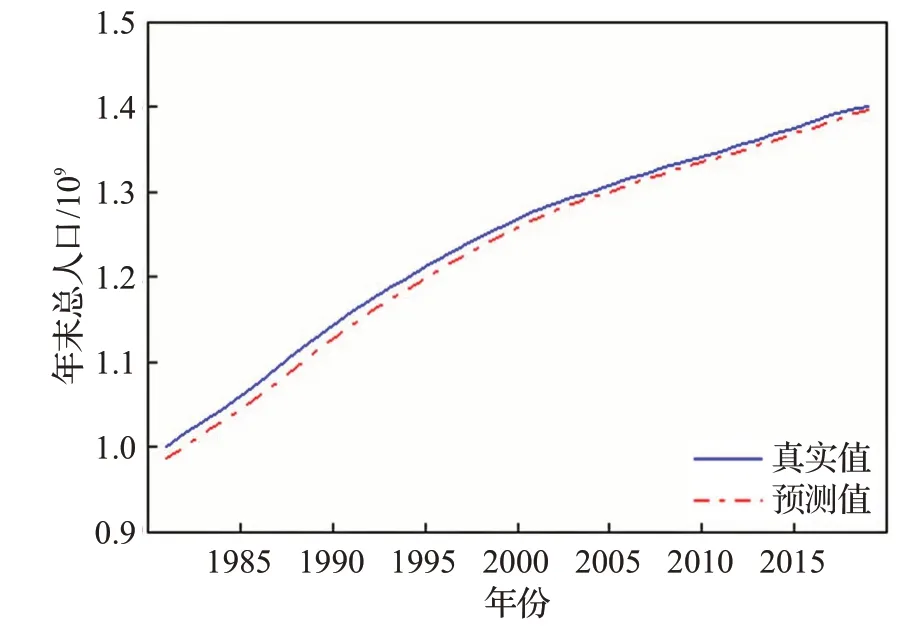
圖8 年末總人口數據預測結果Fig.8 Forecast results of total population data at end of year

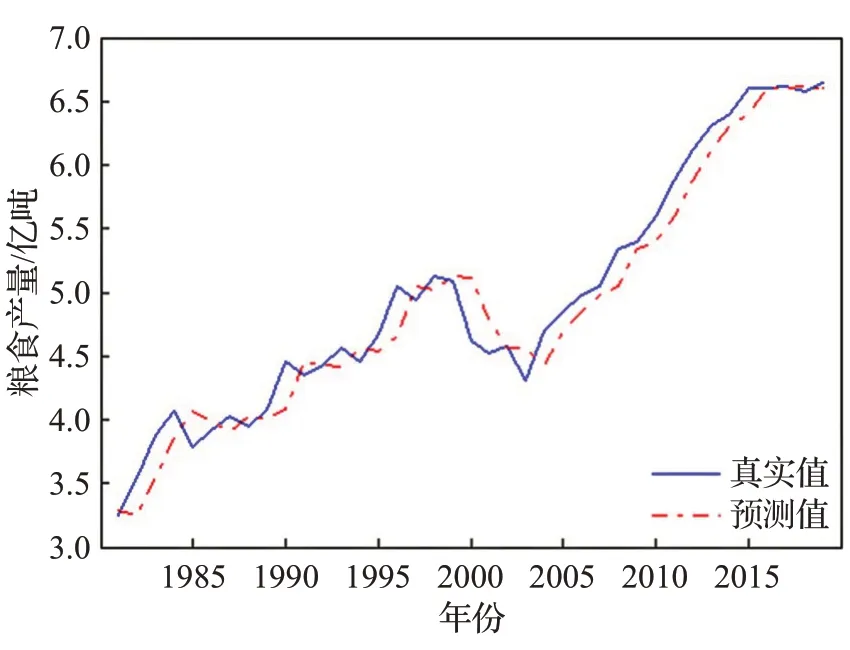
圖9 糧食產量數據預測結果Fig.9 Forecast results of grain yield data

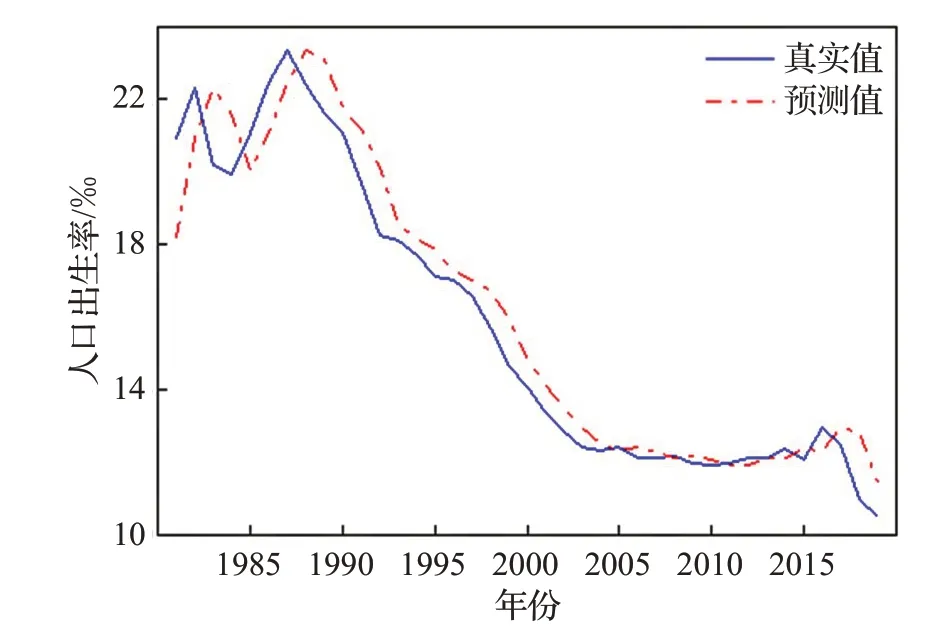
圖10 人口出生率數據預測結果Fig.10 Forecast results of birth rate data

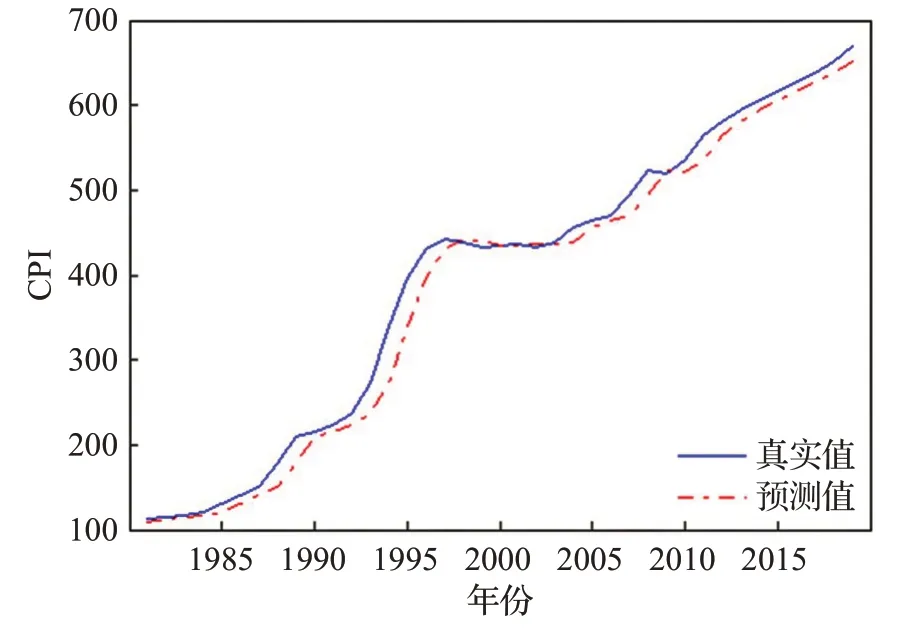
圖11 CPI數據預測結果Fig.11 Forecast results of CPI data

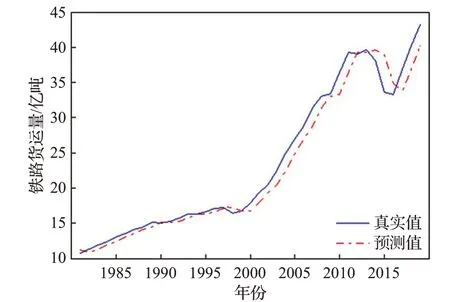
圖12 鐵路貨運量數據預測結果Fig.12 Forecast results of railway freight volume data

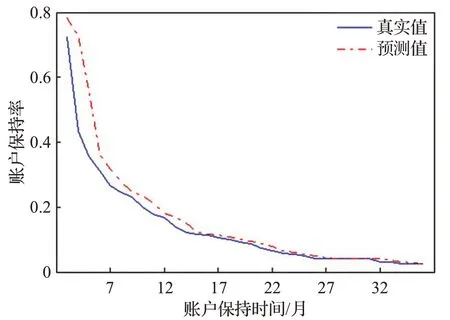
圖13 賬戶保持率數據預測結果Fig.13 Forecast results of account retention rate data

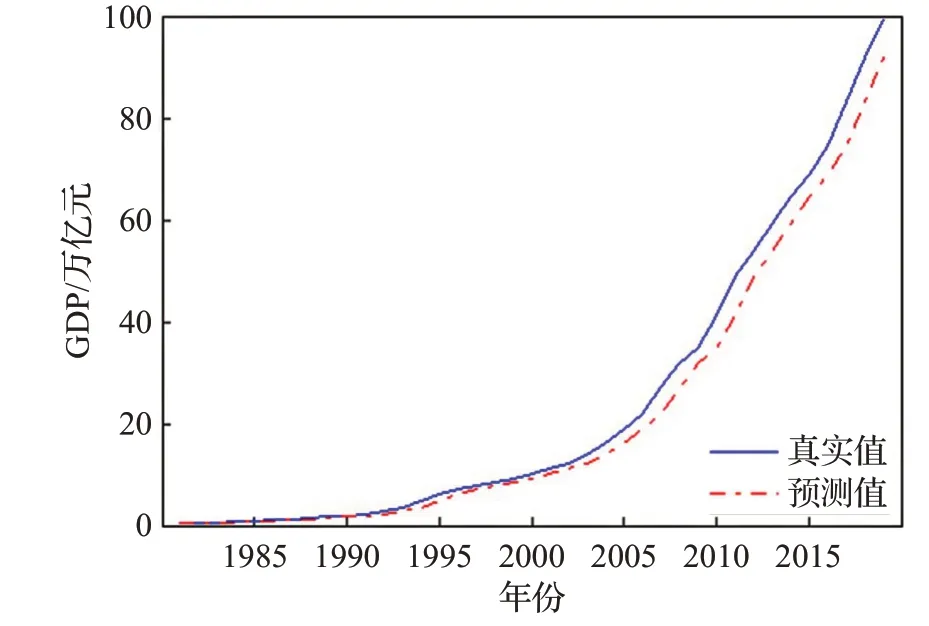
圖14 GDP數據預測結果Fig.14 Forecast results of GDP data

在樣本數據分組的環節，首先按樣本容量的算術根確定組個數進行等距分組，然后遵循小組樣本頻數大等于5的準則，將不符合條件的小組并入相鄰組中；確定分組即組端點后，按標準的卡方擬合優度檢驗程序進行檢驗。

檢驗的計算結果見表3。

由表3可知，在0.01顯著性水平下，12個樣本的絕對預報偏差的檢驗p值均大于0.01。考慮到卡方擬合優度檢驗的結果受數據分組的影響，因此本文的結論是：EABPs模型的絕對預報偏差近似服從指數分布。

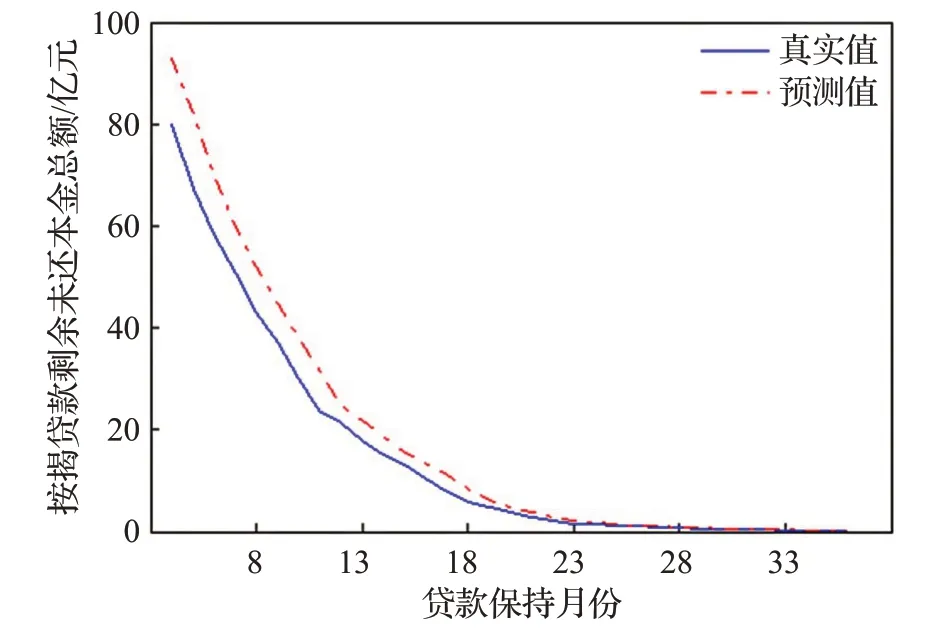
圖15 按揭貸款剩余未還本金總額數據預測結果Fig.15 Forecast results of total outstanding principal data of mortgage loan

3.3 數據波動特征與預報有效性的關系

通常，數學模型描述的是變量的變化規律，觀測數據的波動是影響模型的有效性的客觀因素。

為研究和評價EABPs模型對數據波動的描述和跟蹤能力，建立模型適用性的參考知識，本文定義了描述數據波動特征的穩態指數（steady-state index，STI），和轉折指數（turning index，TI）。

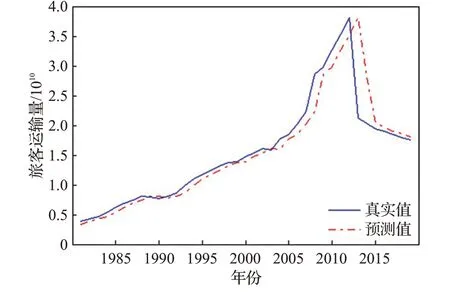
圖16 旅客運輸量數據預測結果Fig.16 Forecast results of passenger traffic volume data

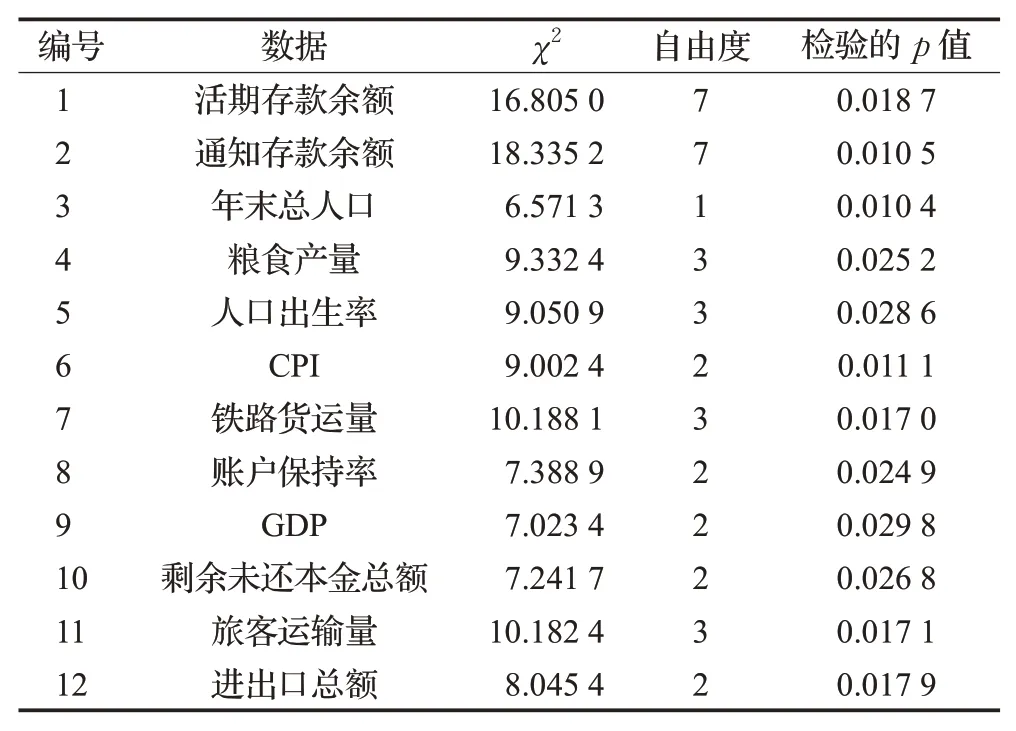
表3 卡方擬合優度檢驗結果Table 3 Chi-square goodness-of-fit test results

穩態指數由數據環比指數的中位數及極差度量，即：

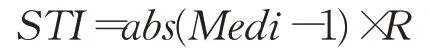
其中，Medi為環比中位數，R為環比極差。

應用中，穩態指數是預判EABPs模型預報誤差的工具。

轉折指數由數據的轉折點在窗口M數據中所占的比例度量，即：

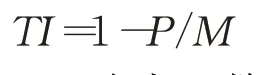
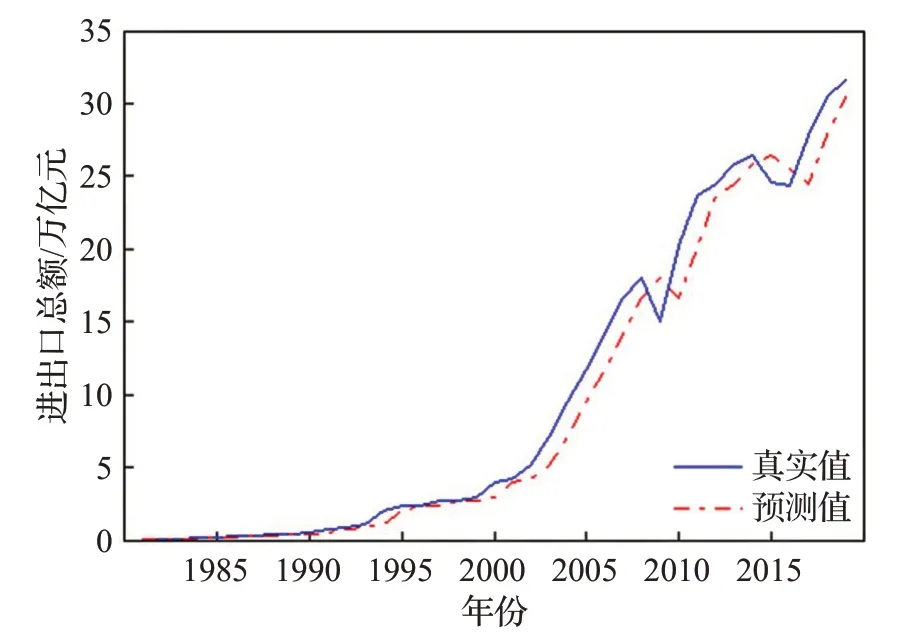
圖17 進出口總額數據預測結果Fig.17 Forecast results of total import and export data

其中，P為窗口數據中轉折點個數，M為模型啟動窗口的數據個數。

應用中，轉折指數是預判EABPs模型預報同態度的工具。

表4給出的是在EABPs模型啟動參數為3的條件下，學習速率尋優后，一個窗口上模型訓練和預測的平均運行時間，即單位運行時間，及穩態指數與預報誤差、轉折指數與同態度的計算結果。

為使觀察更加直觀，繪制了表4中數據穩態指數與預報誤差的散點圖，如圖18；繪制了表4中數據轉折指數與預報同態度的散點圖，如圖19。

由圖18可知，數據穩態指數與預報誤差之間存在近似的混沌分岔特征。分岔[32]就是當參數達到某一臨界值時，系統的定性行為發生“質”變的一種現象。

從穩態指數與預報誤差的散點圖來看，當穩態指數大于0.01時，穩態指數與預報誤差的相關關系發生“質”變。即在穩態指數小于等于0.01時，二者基本呈正相關，且預報誤差小于等于5%；在穩態指數大于0.01時，二者則不再具有相關性。故，二者的相關關系在S TI=0.01處分岔。

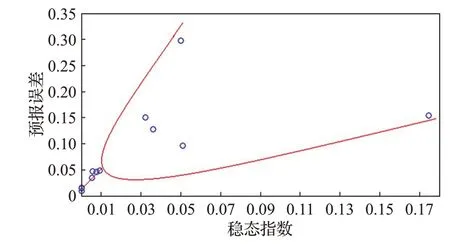
圖18 數據穩態指數與預報誤差散點圖Fig.18 Scatter plot of data steady-state index and forecast error

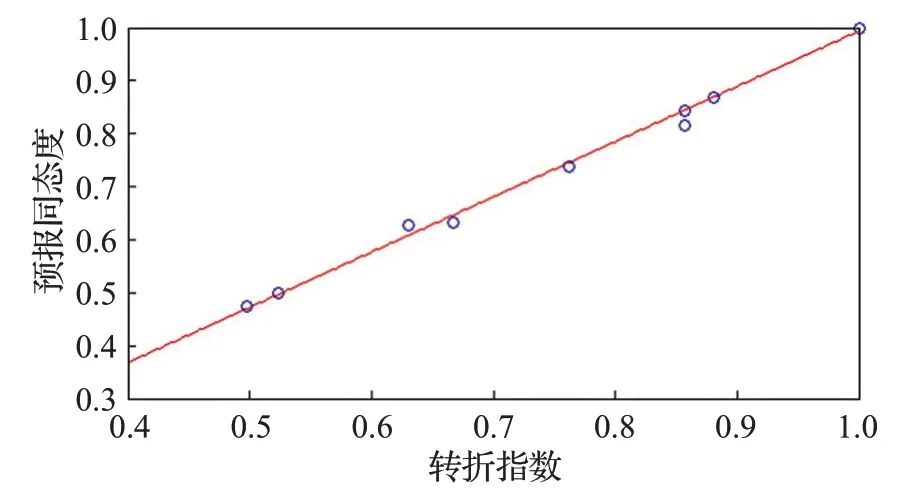
圖19 數據轉折指數與預報同態度散點圖Fig.19 Scatter plot of data turning index and homomorphism rate of forecast

因此，穩態指數可以作為EABPs模型適用性的預估指標，當STI≤0.01時，模型的預報誤差基本上可以控制在5%以內。

由圖19可知，轉折指數與預報同態度呈正相關，且基本相等。因此，由轉折指數可預判EABPs模型預報同態度的取值水平。

限于篇幅，由穩態指數和轉折指數預估EABPs模型預報有效性的方法，本文不做展開討論。

3.4 前端濾波對預報有效性的影響

通常，在數據變異的平穩性受到質疑時需要進行數據降噪處理，以抑制模型與算法對大噪聲或異常波動產生“過敏”響應。數據平穩波動時，數據的環比指數在1附近一定范圍內變化，極差相對較小。由圖18的分析可知，當穩態指數STI≤0.01時，EABPs模型的預報誤差相對穩定在5%以下，預報效果較好。當STI＞0.01時，數據環比特征對EABPs模型預報誤差的解釋作用降低，此時，在EABPs模型的前端引進數據降噪過程，雖不能降低預報的誤差整體水平，但可以在一定程度上抑制由于數據較大波動引起的模型預報行為的“過敏”響應。

為衡量模型預報行為的“過敏”響應程度，本文定義了預報畸變率（distortion rate，DR）：

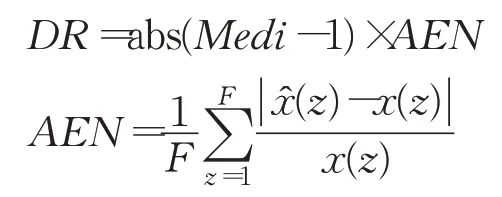
其中，x(z)和分別為時對應的真實值和預測值，即AEN為非同態點的平均預報誤差。

對比濾波數據的預報畸變率和原始數據的預報畸變率，如果DR值減小，則說明加入前端濾波后，抑制了模型預報行為的“過敏”響應。

本文采用的數據濾波算法是移動平均算法的一種變式，不妨稱為重標記均值平滑算法，同EABPs-RNN過程融合，成為前端自動化的數據處理過程。

在模型啟動窗口M上對原始數據進行N項平滑，降噪計算窗口為[1,N](a)，a=1,2,…,N為窗口編號。不妨稱N為噪聲抑制參數，其中，M=2N-1。

記窗口[1,N](a)中數據為。

降噪計算步驟如下：

步驟1計算N個降噪窗口的數據的均值：

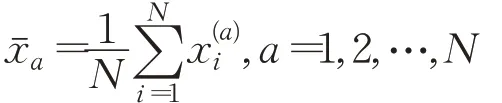
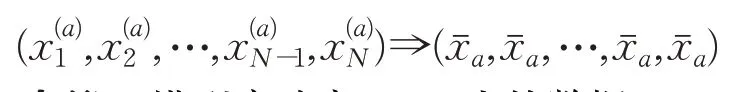
步驟2模型啟動窗口M中的數據：

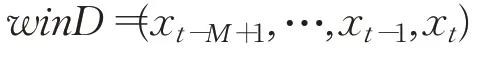
逐點求N重標記的均值，得修勻數據：

其中：

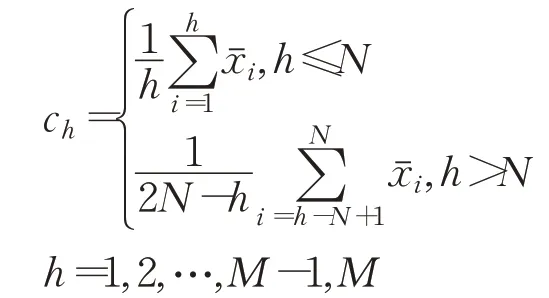
由表3，對STI＞0.01的5個編號為8～12的樣本進行前端除噪。

在模型啟動參數M與噪聲抑制參數N的匹配實驗中發現，當啟動參數M=3，噪聲抑制參數N=2時，5個樣本模型預報結果的中位誤差為0.19最小，中位同態度為1最大。

因此，計算5個樣本在M=3,N=2的條件下，模型預報結果的畸變率，結果見表5。

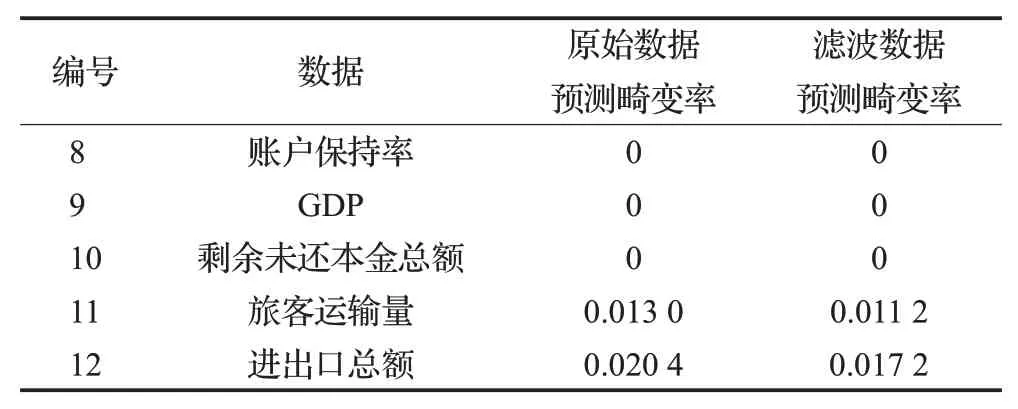
表5 前端濾波對模型預測畸變率的影響Table 5 Influence of front-end filtering on model prediction distortion rate

顯然，加入前端濾波后，預測畸變率明顯下降，即模型的“過敏”行為得到有效改善。其中，編號為8、9和10的樣本數據，濾波前后的預測畸變率均為0，觀察圖13、14、15，發現這三組為強趨勢數據，即數據始終處于上升或下降的狀態，且趨勢明顯增強。

由圖13、14、15可以看出，對于強趨勢時間序列，EABPs模型的預報有一定的系統性偏差；由偏差絕對值近似服從指數分布，不難建立系統性預報偏差的矯正模型；限于篇幅，本文對此不作展開討論。

3.5 EABPs模型同LSTM、GRU模型的對比實驗

3.5.1 與LSTM模型的對比實驗

文獻[19]中，黃婷婷等提出了基于深度學習方法的LSTM神經網絡預測模型（SDAE-LSTM模型）。首先，利用堆疊去噪自編碼從金融時間序列的基本行情數據和技術指標中提取特征，然后，將其作為LSTM神經網絡的輸入對金融時間序列進行預測。文獻[19]中的實驗數據為源自雅虎財經官網的香港恒生指數HSI（Hang Seng index）日調整后收盤價數據（2002-01-02—2014-12-31）。

在SDAE-LSTM模型中，SDAE自編碼的層數為4，每層的神經元個數分別為16、8、8、8，LSTM層數為2，LSTM隱藏層神經元個數分別為8、8，訓練的時間步數為10，即構造的輸入序列的長度為10，batch_size為50，即每50個樣本更新一次網絡參數，訓練次數（epoch）為1 000。同時，采用平均絕對百分比誤差對模型的性能進行評價，并與文獻[33]中的WNN和WPCA-NN預測方法的MAPE值進行比較。其中，WNN、WPCA-NN和SDAE-LSTM模型的平均MAPE值分別為15.5%、4.1%和1.1%。顯然，SDAE-LSTM模型的性能優于WNN和WPCA-NN。

為了對比EABPs與LSTM模型的性能，本文用文獻[19]中的HSI數據對EABPs模型進行訓練并滑動窗口滾動預報。

EABPs模型的啟動參數設置為3。本文沒有重構文獻[19]的模型訓練和預報過程，采用同文獻[19]一致的模型預報誤差評價指標，對預報結果進行評價，評價結果見表6。

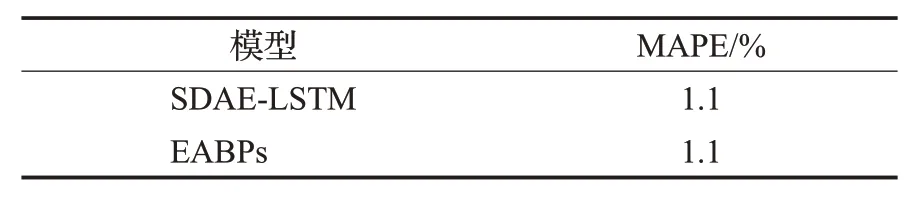
表6 EABPs與LSTM模型的性能比較Table 6 Performance comparison between EABPs and LSTM models

由表6可知，本文EABPs模型的MAPE計算結果為1.1%，與LSTM模型的MAPE值相同。

但是，LSTM模型的網絡結構顯然相對復雜，模型訓練需要大量歷史數據；而EABPs模型的網絡結構單元僅為無隱層BP神經網絡，輕啟動無需對大樣本數據集進行訓練。

3.5.2 與GRU模型的對比實驗

文獻[24]中，張金磊等提出了基于差分運算與GRU神經網絡相結合的金融時間序列預測模型。首先，對金融時間序列進行差分操作，然后，將處理后的數據輸入到GRU神經網絡進行預測。

文獻[24]中的實驗數據為源自雅虎財經官網的標準普爾（S&P）500股票指數日調整后收盤價數據（1950-01-03—2018-03-14）。

文獻[24]中采用均方根誤差RMSE對模型的性能進行評價，并與文獻[34]中的ARIMA模型的RMSE值進行比較。其中，ARIMA和GRU模型的平均RMSE值分別為55.30和15.12。顯然，GRU模型的性能優于ARIMA。

為了對比EABPs與GRU模型的性能，本文用文獻[24]中的S&P500數據對EABPs模型進行訓練并滑動窗口滾動預報。

EABPs模型的啟動參數設置為3.本文沒有重構文獻[24]的模型訓練和預報過程，采用同文獻[24]一致的模型預報誤差評價指標，對預預報結果進行評價，評價結果見表7。

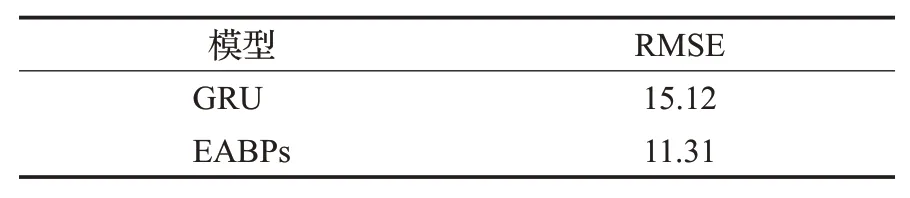
表7 EABPs與GRU模型的性能比較Table 7 Performance comparison between EABPs and GRU models

由表7可知，本文EABPs模型的RMSE結果為11.31，與GRU模型相比，降低了25.2%。同時，文獻[24]中提到，GRU模型需要訓練781個參數，而EABPs模型只需訓練8個參數。更重要的是，GRU模型的網絡結構較EABPs模型復雜得多。

故綜合表6和表7的結果，在一步預報問題中，EABPs模型比LSTM模型和GRU模型更為適用。

4 結語

綜上討論，對本文的工作總結如下：

（1）本文研究創新性地提出了基于微分動力學方程（1）的EABPs模型以及EABPs-RNN預報過程。實證分析表明，EABPs模型具有明確的“輕啟動”性質，網絡結構簡單，有一定的預報可靠性。EABPs模型隨泛鵬天地的業務活動在國內某商業銀行的試用結果表明，在隔夜頭寸預報中表現良好，能夠為業務決策提供有效的參考信息。

（2）本文創新性地提出了穩態指數、轉折指數，為分析數據的環比波動特征和模型預報有效性之間的關系提供了一種思想方法，可供同類研究參考。

（3）本文基于幾何學思想原理改進了移動平均濾波算法，創新性地提出了畸變率指標，為度量和評價前端濾波對模型預報結果的影響提供了可參考的技術方法。

（4）實證分析表明，EABPs模型的絕對預報殘差近似服從指數分布，發生大預報誤差事件是可控的；在穩態指數STI≤0.01，可以預估模型預報的誤差水平，這時平均絕對百分比誤差可以控制在5%以內；由轉折指數可以預估模型預報的同態度。對于穩態指數STI＞0.01的時間序列，模型前端降噪可以抑制模型預報的“過敏”行為，能夠更好地描述序列的趨勢規律。

（5）同NLP框架下的LSTM模型和GRU模型的對比實驗雖不充分，但同文獻[19]和文獻[24]的比較分析結果表明，EABPs模型在時間序列短期預測問題中有更好的表現。

限于篇幅，本文僅討論了EABPs模型一步預測問題；項目組研究了基于EABPs模型的多步預測問題，方法和結論另文報告。