基于窗函數(shù)頻譜設(shè)計(jì)NLFM信號(hào)波形的方法性能分析

馬 蘭 張苡寧 李照照 井 偉 陳倆興

(1.西安電子工程研究所 西安 710100；2.中國(guó)人民解放軍32382部隊(duì) 北京 100071)

0 引言

由于NLFM信號(hào)脈壓時(shí)無需作加權(quán)處理便可獲得較低的副瓣，近年來廣泛受到關(guān)注。相較于LFM信號(hào)，NLFM信號(hào)的改進(jìn)主要是將經(jīng)過匹配濾波后的信號(hào)主副瓣比提高，同時(shí)減小脈壓時(shí)的SNR損失。本文是基于相位逗留原理，首先通過利用窗函數(shù)的頻譜來求出群時(shí)延函數(shù)，對(duì)群時(shí)延函數(shù)作插值擬合將頻率函數(shù)估計(jì)出來，再根據(jù)NLFM信號(hào)相位函數(shù)與頻率函數(shù)的關(guān)系，可對(duì)頻率函數(shù)累加求和計(jì)算出相位函數(shù)，最后得到NLFM信號(hào)波形。

文獻(xiàn)[1]主要是根據(jù)脈壓輸出波形峰值主副瓣比或主瓣寬度的實(shí)際需求來設(shè)計(jì)NLFM信號(hào)，采用的方法是動(dòng)態(tài)優(yōu)選法，該方法運(yùn)算量小，靈活性高，但設(shè)計(jì)的前提是已知脈壓結(jié)果的主副瓣比或主瓣寬度[1]。文獻(xiàn)[2]是從NLFM信號(hào)的最小峰值旁瓣抑制器出發(fā)，采用凸優(yōu)化方法進(jìn)行實(shí)現(xiàn)并設(shè)計(jì)了一種新的NLFM信號(hào)，通過迭代法進(jìn)一步抑制了信號(hào)的距離旁瓣。該方法主要適用于小時(shí)寬帶寬積的NLFM信號(hào)的設(shè)計(jì)[2]。文獻(xiàn)[3]是通過設(shè)計(jì)振幅窗函數(shù)并對(duì)NLFM信號(hào)進(jìn)行脈壓處理來獲得較低的副瓣電平，該方法的缺點(diǎn)是幅度加權(quán)會(huì)帶來一定的SNR損失[3]。

為更好地滿足實(shí)際需求，本文對(duì)所設(shè)計(jì)的NLFM信號(hào)進(jìn)行了譜修正濾波處理[4-5]，在主瓣展寬和主副瓣比可接受的范圍內(nèi)，進(jìn)一步降低了信號(hào)的旁瓣電平，改善了NLFM信號(hào)的脈壓性能。同時(shí)，對(duì)NLFM信號(hào)的多普勒容限進(jìn)行了驗(yàn)證，實(shí)驗(yàn)結(jié)果表明，NLFM信號(hào)對(duì)多普勒頻移敏感[6-8]。

1 基于窗函數(shù)頻譜設(shè)計(jì)NLFM信號(hào)的基本原理

假設(shè)NLFM信號(hào)的頻譜為

(1)

由于匹配濾波器的傳輸函數(shù)h(t)與輸入信號(hào)s(t)之間滿足關(guān)系式(2)為

h(t)=ks*(t0-t)

(2)

其中，k為一常數(shù)，一般令其為1，t0表示回波信號(hào)的時(shí)延，一般都假設(shè)為0，因此，式(2)可以簡(jiǎn)寫為

h(t)=s*(-t)

(3)

則匹配濾波器的頻域表達(dá)式為

H(f)=S*(f)

(4)

故信號(hào)經(jīng)過頻域脈壓之后的頻域輸出為

Y(f)=S(f)·H(f)=S(f)·S*(f)=|S(f)|2

(5)

根據(jù)相位逗留原理，脈壓輸出Y(f)會(huì)與一個(gè)理想的窗函數(shù)W(f)等價(jià)，即

Y(f)=|S(f)|2=W(f)

(6)

其中，W(f)為理想窗函數(shù)的頻域表達(dá)式。

根據(jù)信號(hào)相位函數(shù)θ(f)與信號(hào)頻譜S(f)的關(guān)系

(7)

以及群時(shí)延函數(shù)的頻域表達(dá)式T(f)與相位函數(shù)的一階導(dǎo)數(shù)θ′(f)的關(guān)系為

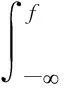
(8)

可知，群時(shí)延函數(shù)具有如表達(dá)式(9)所示。

(9)

其中，B為信號(hào)帶寬，Ka為常數(shù)，其表達(dá)式為

(10)

其中，T為信號(hào)脈沖寬度。

由于頻率函數(shù)f(t)是群時(shí)延函數(shù)T(f)的反函數(shù)，即

f(t)=T-1(f) (-T/2≤t≤T/2)

(11)

由于常見的窗函數(shù)頻譜表達(dá)式W(f)均是由一些正余弦項(xiàng)組成，故對(duì)其進(jìn)行積分得到的群時(shí)延函數(shù)表達(dá)式T(f)也必定是一些與正余弦相關(guān)的項(xiàng)，求其反函數(shù)一般較為困難。通常，頻率函數(shù)f(t)的求取是對(duì)群時(shí)延函數(shù)T(f)進(jìn)行插值擬合來近似獲得。具體如下：

假設(shè)dt為采樣間隔，df為均分帶寬，tf為群時(shí)延函數(shù)元素值，則頻率函數(shù)f(t)的元素組成近似可以表示為

(12)

最后，根據(jù)相位函數(shù)φ(t)與頻率函數(shù)f(t)的關(guān)系

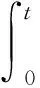
(13)

對(duì)頻率函數(shù)累加求和得到相位函數(shù)各元素值。

假設(shè)NLFM信號(hào)的表達(dá)式為

y(t)=a(t)ejφ(t)

(14)

令幅度函數(shù)a(t)=1，并將相位函數(shù)φ(t)代入，就可得到NLFM信號(hào)表達(dá)式。

2 NLFM信號(hào)的低旁瓣脈沖壓縮

2.1 NLFM信號(hào)的脈壓性能仿真分析

假設(shè)在NLFM信號(hào)的設(shè)計(jì)過程中分別選擇Hanning窗、Hamming窗和Blackman窗的頻譜進(jìn)行設(shè)計(jì)，則它們的頻域表達(dá)式分別為

W1(f)=0.54-0.46cos(2πf/B)

(15)

W2(f)=0.42-0.5cos(2πf/B)+0.08cos(4πf/B)

(16)

W3(f)=0.5-0.5cos(2πf/B)

(17)

結(jié)合式(9)和式(10)分別得到對(duì)應(yīng)的群時(shí)延函數(shù)為

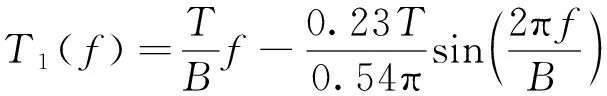
(18)

(19)

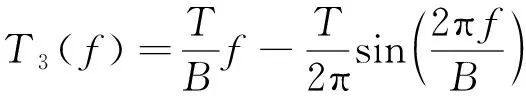
(20)

根據(jù)式(12)的插值擬合方法，可以得到頻率函數(shù)對(duì)應(yīng)的近似S型曲線。

假設(shè)雷達(dá)仿真參數(shù)設(shè)計(jì)如表1所示。

表1 仿真參數(shù)設(shè)計(jì)1

具體設(shè)計(jì)過程如下：

1)Hanning窗函數(shù)下的仿真分析：

圖1 Hanning窗頻譜波形

圖2 群時(shí)延函數(shù)曲線

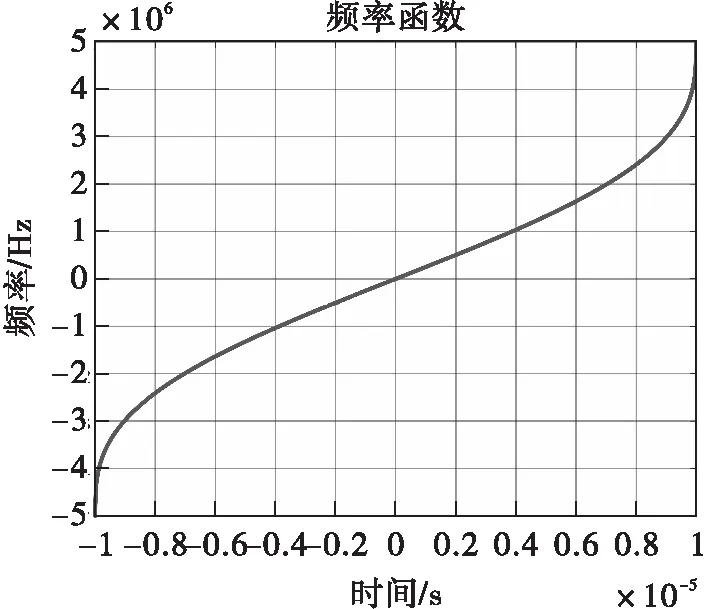
圖3 近似頻率函數(shù)曲線

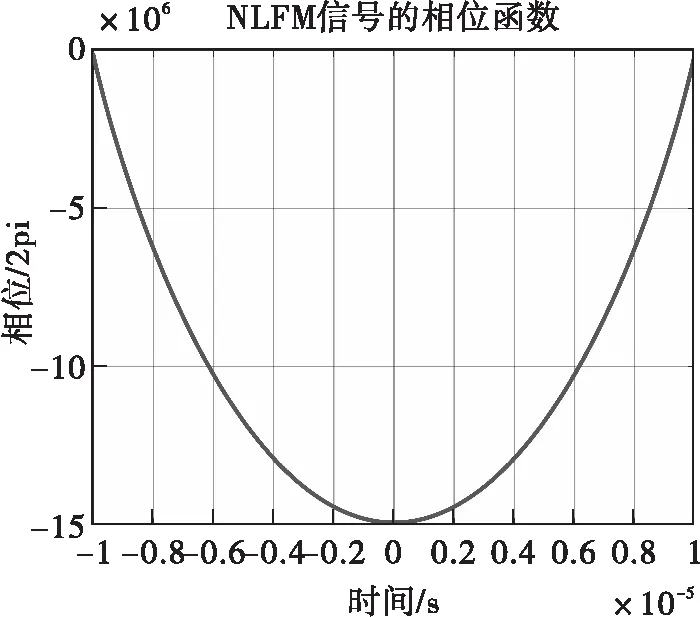
圖4 相位函數(shù)曲線

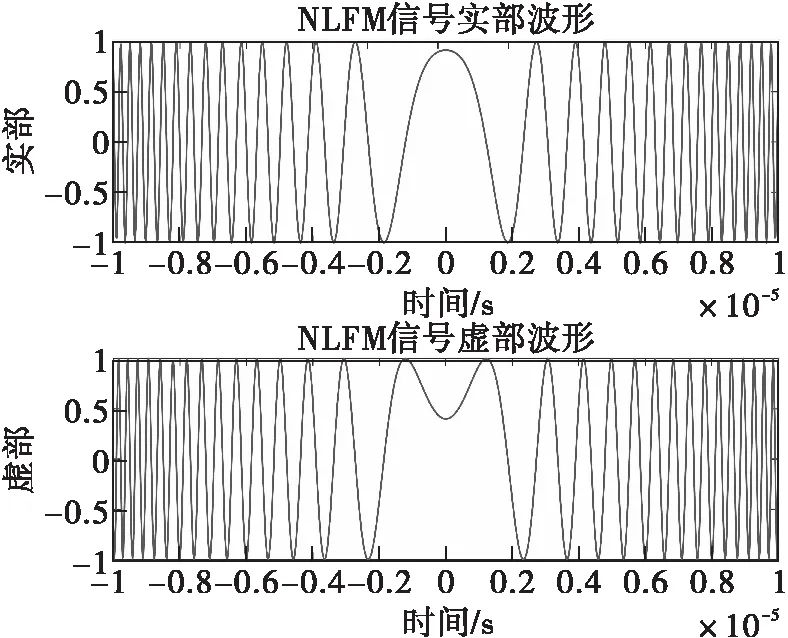
圖5 NLFM信號(hào)波形

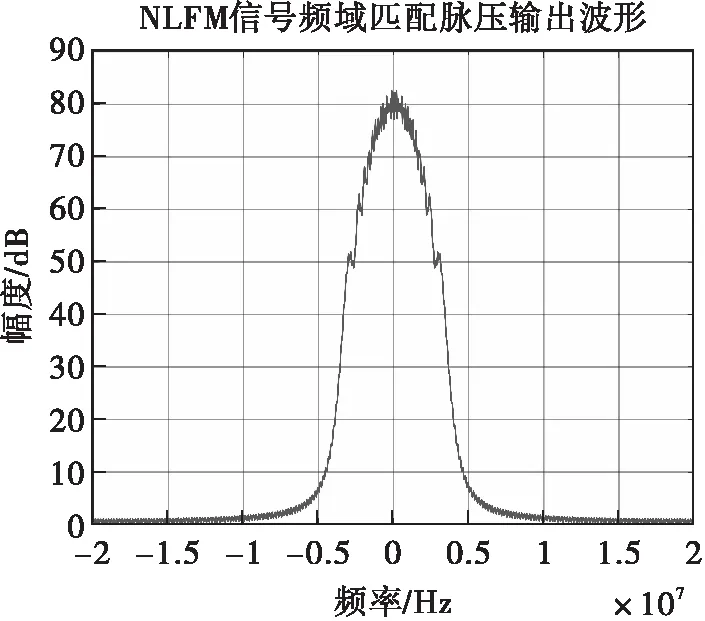
圖6 NLFM信號(hào)頻譜特性

圖7 NLFM信號(hào)頻域匹配脈壓波形

2)Hamming窗函數(shù)下的仿真分析：

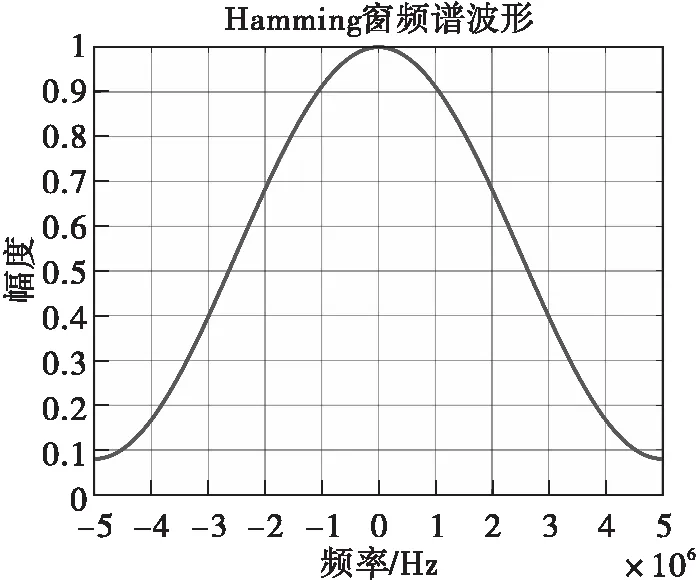
圖8 Hamming窗頻譜波形

圖9 群時(shí)延函數(shù)曲線

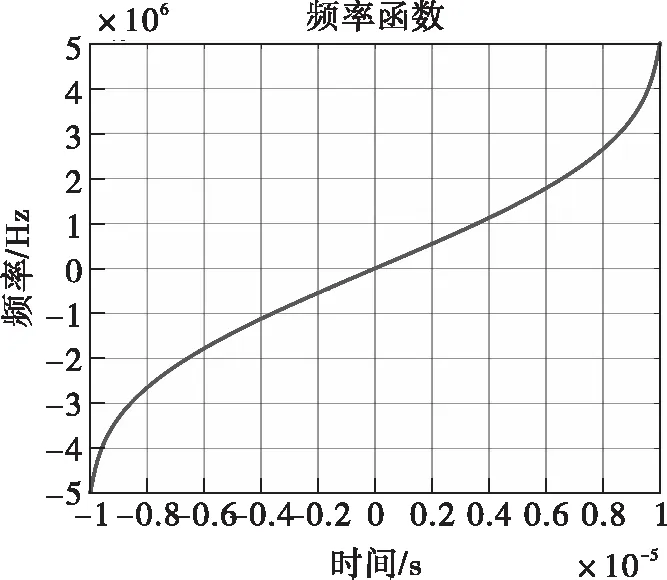
圖10 近似頻率函數(shù)曲線

圖11 相位函數(shù)曲線

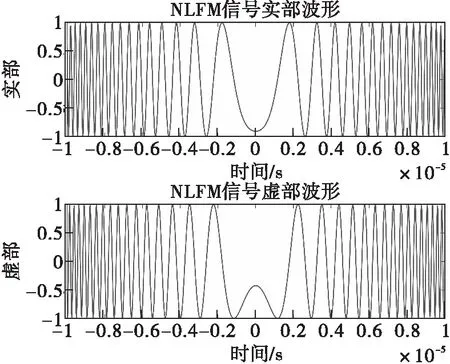
圖12 NLFM信號(hào)波形

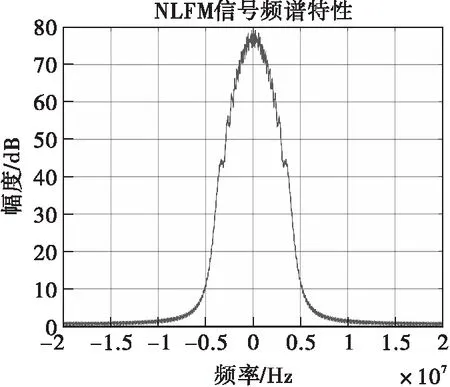
圖13 NLFM信號(hào)頻譜特性

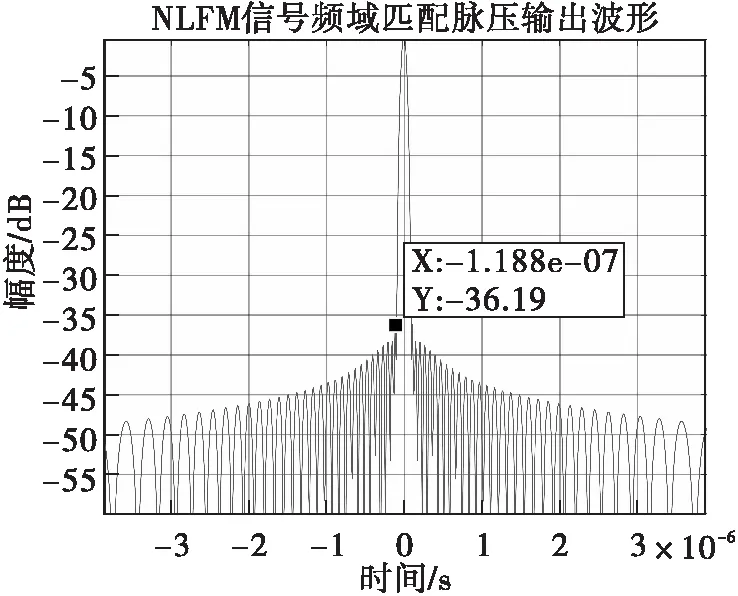
圖14 NLFM信號(hào)頻域匹配脈壓波形

3)Blackman窗函數(shù)下的仿真分析：

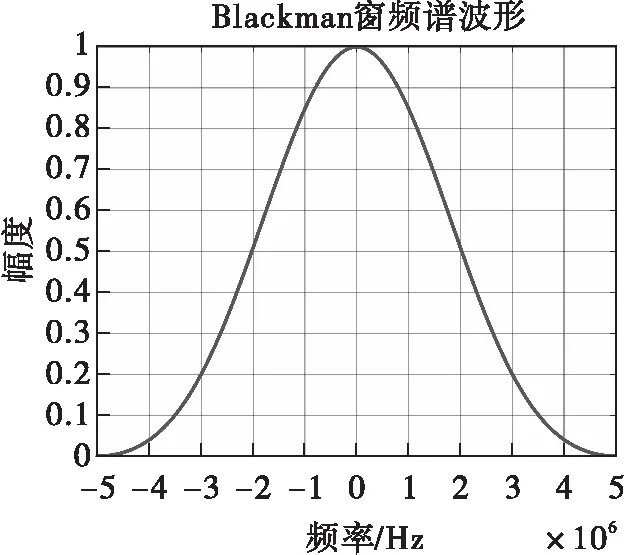
圖15 Blackman窗頻譜波形

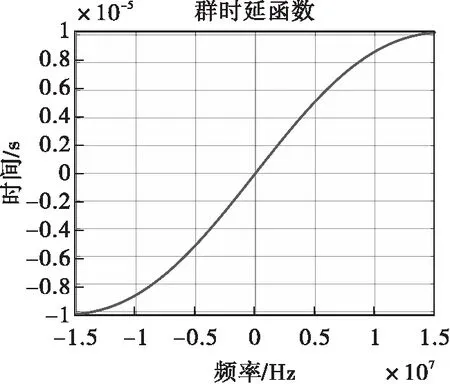
圖16 群時(shí)延函數(shù)曲線

圖17 近似頻率函數(shù)曲線

圖18 相位函數(shù)曲線

圖19 NLFM信號(hào)波形

圖20 NLFM信號(hào)頻譜特性

圖21 NLFM信號(hào)頻域匹配脈壓波形

比較三種窗函數(shù)下的仿真結(jié)果可以看出，在該組雷達(dá)設(shè)計(jì)參數(shù)下，利用Hamming窗設(shè)計(jì)的NLFM信號(hào)具有較好的脈壓性能，其頻域匹配脈壓波形主副瓣比僅為-36.19dB。相比于LFM信號(hào)，NLFM信號(hào)具有較好的低旁瓣電平脈壓性能。

2.2 譜修正后NLFM信號(hào)的脈壓性能仿真分析

由于在NLFM信號(hào)波形的設(shè)計(jì)過程中，求取頻率函數(shù)采用了插值擬合的方法，因此最終得到的信號(hào)波形與理論結(jié)果存在一定的偏差。為進(jìn)一步降低NLFM信號(hào)的旁瓣電平，使其信號(hào)頻譜更接近于理想窗函數(shù)，考慮到直接加權(quán)會(huì)引起SNR損失，有人提出了采用譜修正濾波器[9-10]來改善NLFM信號(hào)脈壓性能。

譜修正濾波原理如圖22所示，其中，s(n)表示NLFM信號(hào)的離散形式；h′(n)表示譜修正濾波器的離散形式；w(n)表示理想窗函數(shù)的離散形式。

圖22 譜修正濾波原理框圖

假設(shè)譜修正濾波后的信號(hào)輸出為理想窗函數(shù)，則可以得到譜修正濾波器的頻域表達(dá)式為

(21)

其中，W(f)為理想窗函數(shù)頻域表達(dá)式；S(f)為設(shè)計(jì)的NLFM信號(hào)頻域表達(dá)式。

假設(shè)雷達(dá)仿真參數(shù)設(shè)計(jì)如表2所示。

表2 仿真參數(shù)設(shè)計(jì)2

仿真結(jié)果如圖23至圖26所示。

圖23 NLFM信號(hào)頻譜特性

圖24 譜修正后NLFM信號(hào)頻譜特性

圖25 NLFM信號(hào)匹配脈壓結(jié)果

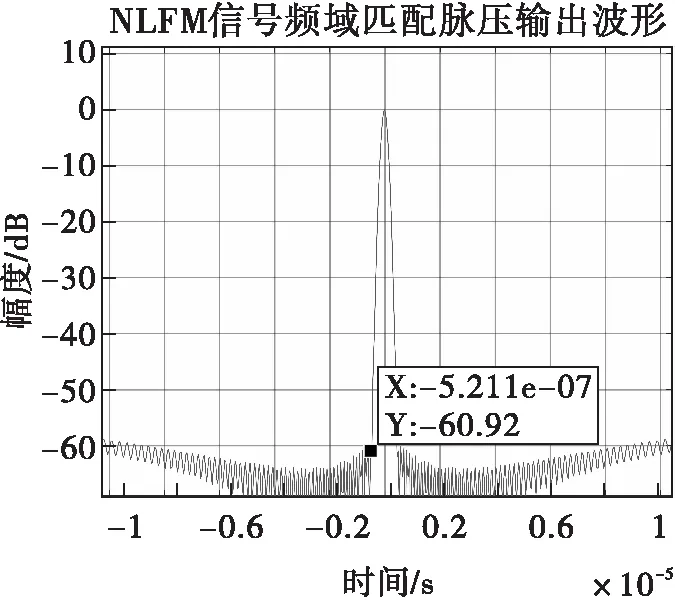
圖26 NLFM信號(hào)譜修正濾波脈壓結(jié)果

對(duì)比圖25和圖26可以看出，相較于直接對(duì)NLFM信號(hào)作匹配脈壓，經(jīng)過譜修正濾波后NLFM信號(hào)的副瓣電平明顯降低，大約為16dB左右，故譜修正濾波可以明顯改善NLFM信號(hào)的脈壓性能。

由于實(shí)際脈壓結(jié)果受很多因素的影響，下面針對(duì)信號(hào)時(shí)帶積和采樣率對(duì)脈壓結(jié)果的影響進(jìn)行對(duì)比分析。

如表3所示，分別選擇時(shí)帶積為480和600，采樣率為fs=2B和fs=4B，且每種情況下分別選擇Hamming、Blackman和Hanning窗函數(shù)進(jìn)行譜修正濾波處理，仿真結(jié)果如表4所示。

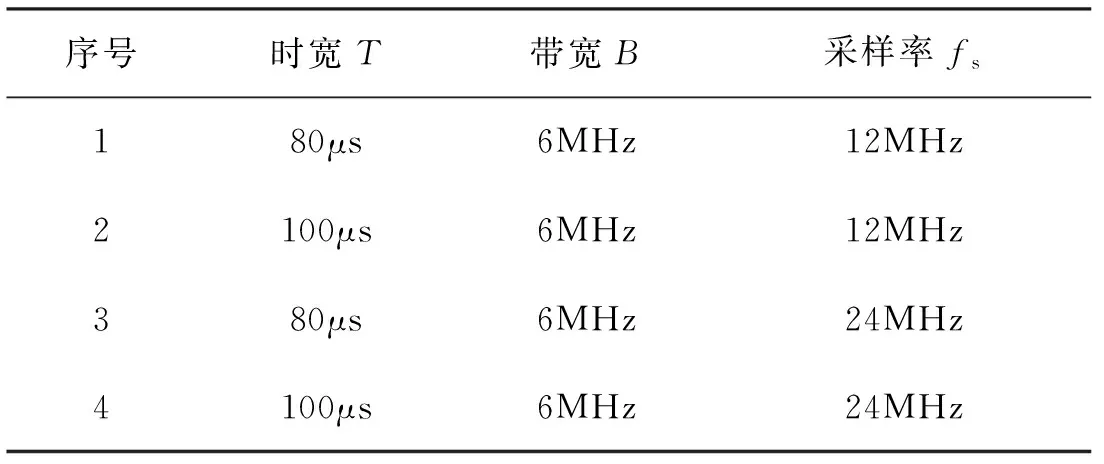
表3 仿真參數(shù)設(shè)計(jì)3

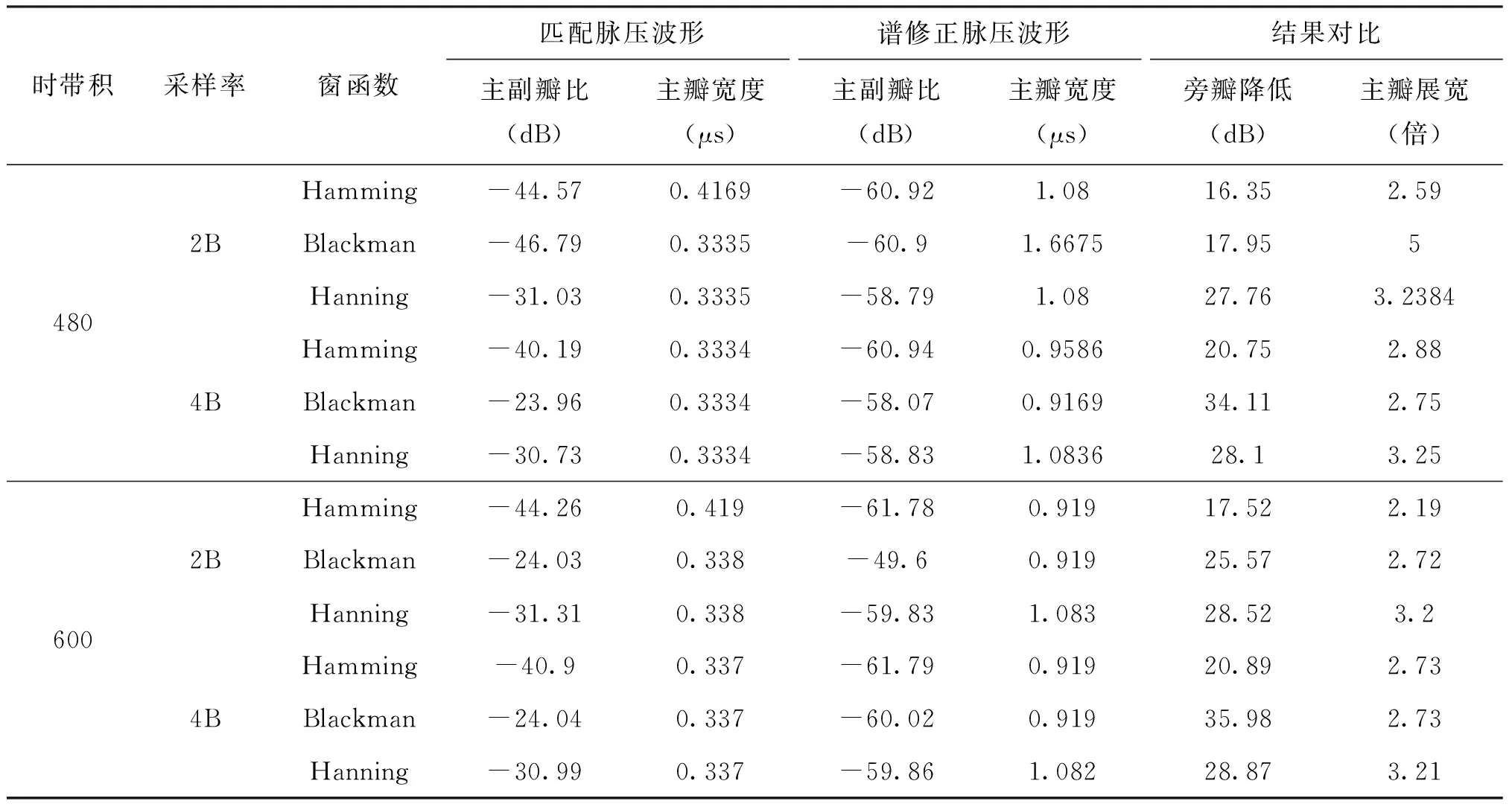
表4 不同因素對(duì)NLFM信號(hào)脈壓性能的影響對(duì)比分析

從表4可以看出，隨著時(shí)帶積的增加，NLFM信號(hào)的脈壓性能越來越好；隨著采樣率的增加，譜修正濾波之后NLFM信號(hào)的旁瓣電平被進(jìn)一步抑制，且當(dāng)fs=2B時(shí)，選取的三種窗函數(shù)中Hanning窗的旁瓣抑制性能最好；當(dāng)fs=4B時(shí)，Blackman窗的旁瓣抑制性能最好；譜修正濾波器的引入可以改善NLFM信號(hào)的脈壓性能，但同時(shí)也帶來了一定的主瓣展寬。

綜合考慮，在脈壓波形主瓣展寬可接受范圍內(nèi)，通過譜修正濾波降低NLFM信號(hào)的副瓣電平是可行的。

3 NLFM信號(hào)的多普勒容限

假設(shè)仿真參數(shù)設(shè)計(jì)如表1所示，多普勒頻率fd分別取±10kHz、±50kHz，則加入fd后NLFM信號(hào)的匹配脈壓結(jié)果如圖27所示。

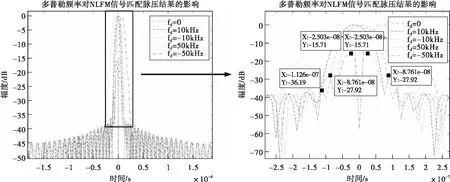
圖27 多普勒頻率對(duì)NLFM信號(hào)匹配脈壓結(jié)果的影響

根據(jù)仿真結(jié)果可以看出，當(dāng)多普勒頻率fd=±10kHz時(shí)，NLFM信號(hào)匹配脈壓波形的主副瓣比由-36.19dB增加至-27.92dB；當(dāng)多普勒頻率fd=±50kHz時(shí)，輸出波形主副瓣比增加至-15.71dB。故當(dāng)回波信號(hào)中有較大的多普勒頻移時(shí)，匹配濾波器將不能起到較好的脈沖壓縮作用，即NLFM信號(hào)是一種多普勒敏感信號(hào)。

4 結(jié)束語

本文基于相位逗留原理，利用不同窗函數(shù)頻譜對(duì)NLFM信號(hào)波形進(jìn)行了設(shè)計(jì)，比較了不同窗函數(shù)頻譜下設(shè)計(jì)的NLFM信號(hào)脈壓性能。實(shí)驗(yàn)結(jié)果表明，Hamming窗具有更好的脈壓性能，且相較于LFM信號(hào)，NLFM信號(hào)匹配脈壓結(jié)果具有較好的低旁瓣電平。同時(shí)，仿真分析了多普勒頻移對(duì)NLFM信號(hào)匹配脈壓波形的影響，仿真結(jié)果驗(yàn)證了NLFM信號(hào)是一種多普勒敏感信號(hào)。