一類三維分段光滑系統(tǒng)的穿越極限環(huán)

鄭瑩瑩, 陳興武

(四川大學(xué)數(shù)學(xué)學(xué)院, 成都 610064)

1 Introduction

In recent years, discontinuous piecewise-smooth(DPWS)systems have enjoyed widespread application such as mechanical systems with friction, switched electronic systems, and control systems[1, 2].For DPWS systems, bifurcations of limit cycle are also an important problem[3, 4].In this paper we consider a 3D discontinuous piecewise-smooth system defined by ordinary differential equations.Here the vector field is discontinuous along a hypersurface in its 3D phase space and, sometimes, this hypersurface is called aswitchingmanifold.For 3D discontinuous piecewise-smooth systems, an important and interesting type of singularity is two-fold singularity, which is a point on the switching manifold and at which the vector fields on both sides are tangent with the switching manifold.Actually, as indicated in Refs.[5-7]each sub-vector field on different sides has a set of tangential singularities on the switching manifold and this set is a curve, which is also calledtangencycurve.So, a two-fold is actually an intersection point of two tangency curves of sub-vector fields.Additionally, under some non-degenerate conditions, this two-fold is said to beregular, otherwise, we say this two-fold isdegenerate.

The dynamical behavior was analyzed near a regular two-fold for a 3D discontinuous piecewise-smooth system in Refs.[8-10]by using Filippov’s convention[11].Considering the degeneracy of two-fold, Q2-singularityhad been presented in Ref.[12].Further, by the tangency degree of those two tangency curves, the classification of degenerate two-fold was given in Ref.[5]as 1-degenerate two-fold(Q2-singularity)and 2-degenerate two-fold, the normal form for systems having degenerate two-fold was also provided, which shows that under perturbations a 1-degenerate two-fold may disappear or split into two regular two-folds and of course some interesting sliding bifurcations happen.A truncation of generic unfolding of a normal form having a 1-degenerate two-fold was reduced as

(1)

in Ref.[13],whereX=(x,y,z)T,c1,c2,μ∈R.It was proved in Ref.[13]that system(1)has a family of non-isolated crossing periodic orbits whenc1+c2=0.Fixingc1=-c2=-1/4 and adding termsax,azinF+(X)in(1), it was obtained in Ref.[7]that

(2)

wherea,μ∈Randa≠0.The existence and number of crossing limit cycles(CLCs for abbreviation)for system(2)were investigated in Ref.[7].Although some terms are added in(2),c1andc2are restricted as-1/4 and 1/4 respectively.We wonder whether there are still CLCs without this restriction, i.e, generalc1,c2satisfyingc1+c2=0.

In this paper, we study the existence and number of CLCs for system

(3)

We show the crossing and sliding regions whenμ<0,μ=0, andμ>0 respectively in Fig.1.

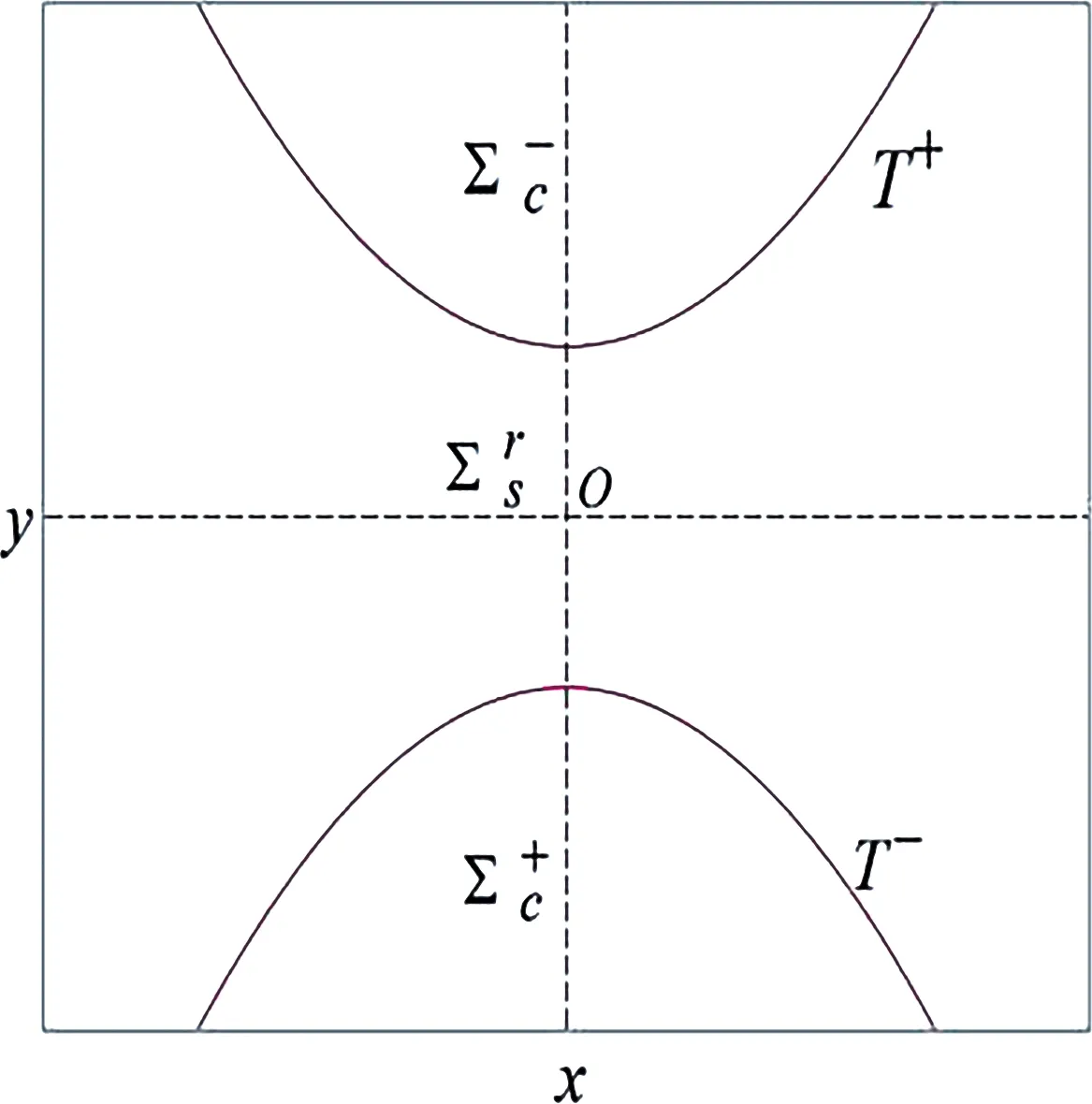
(a)μ<0

We get the results about CLCs of system(3)in the following theorem.

(4)

and

(5)

In Theorem 1.1, results about the existence and number of CLCs as well as their birth given in Ref.[7]are generalized from the casec1=-c2=-1/4 to the casec1+c2=0.

This paper is organized as following.In Section 2, we introduce some basic definitions of DPWS systems.In Section 3, we provide a proof for Theorem 1.1.In Section 4, we present some remarks and give examples to show the existence of CLCs.

2 Preliminaries

In this section, we introduce some basic definitions about DPWS systems.For a 3D DPWS system

(6)

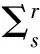
which is tangent to theΣ.Moreover

When a pointpis a fold for bothF+andF-, the point is called two-fold.Generically,T+andT-are transverse at this point, and more precisely classification is shown as follows.

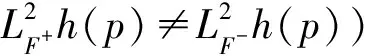
3 Proof of the main result

In this section, we give a detailed proof of Theorem 1.1.

y+(t)=y0+t,

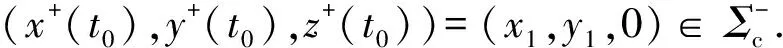
x-(t)=x1-ct,

y-(t)=y1-t,

Fig.2 The trajectories and return map for system(3)

(7)

hereg1(τ),g2(τ)are defined in(4).Because

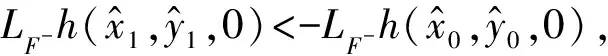
fixed point only needs to satisfy first three conditions.For writing conveniently, we write the third formula in(7)asg3(τ).Considering functionφ(τ), we obtain the derivative

Lemma3.2Fora>2c2, there exists a constantτsnsuch thatφ(τ)decreases for 0<τ<τsnand increases forτ>τsn.Fora≤2c2, the functionφ(τ)increases.

ProofBy the definition ofφ, we get

limτ→0+φ(τ)=-μ

and

(f1(τ)-f2(τ)),

where

Consider the casea>2c2firstly, Since 2c2+3a+2c2(e-aτ+eaτ)>0 forτ∈(0,+∞), the zeros of ?φ(τ)/?τare given by the intersection of functionsf1,f2.Clearly,

The derivatives off2(τ)aboutτare

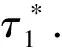
On the other hand, since limτ→+∞φ(τ)=+∞, functionφ(τ)+μhas a unique zero, calledτ0, andτsn<τ0.After we prove the monotonicity of functionφ(τ), we analyze the number of CLCs, which is equivalent to the number of zeros ofφ(τ).In the following, we give a proof of Theorem 1.1.

ProofofTheorem1.1By the definition ofg3(τ), we rewriteg3(τ)as

where

Then, forτ∈(0,+∞)we have

We obtain that functiong3(τ)>0.Therefore, in order to make sure that the fixed points lie in the crossing region,we only require thatτ∈Ω(c,a), where Ω(c,a)is defined in the statement of this theorem.Further, by Lemma 3.1 the necessary and sufficient condition given in this theorem is obtained for the existence of CLCs.

In the following, we prove that the maximum number of CLCs of system(3)is 2 and it is reachable.Fora≤2c2,φ(τ)is an increasing function.Thusφ(τ)has at most one zero,i.e.,system(3)has at most one CLC in this case.

Fora>2c2,φ(τ)has at most two zeros, which implies that there exists at most two CLCs.By the proof of Lemma 3.2,we getτsn=f2(τsn).Associating with expressions ofg1,g2andf2, we obtain

H(τsn)<0,

where

H(τsn)=16ac4e3aτsn+

3c2(4c4+4ac2+9a2)e2aτsn+

6a(4c4+4ac2+3a2)eaτsn-

12c6+20ac4+21a2c2.

Therefore,τsn∈Ω(c,a).

On the other hand, by the expression ofφ(τ)given in(4)we get thatφ(τsn)=-εwhen

In this section, we provide some remarks to understand more details about the birth and disappearance of CLCs.By the expressions ofg1(τ),g2(τ)andφ(τ), it is not hard to check that

which implies that

(i)zeros ofg1(τ),φ(τ)+μ, ?φ(τ)/?τtend to 3/(4c2),3/(2c2),3/(4c2)respectively asa→+∞;

(ii)zeros ofg2(τ)tend to 1/c2asa→-∞;

(iii)zeros ofg1(τ),g2(τ)tend to 3/c2asa→0.

This is consistent with the properties of these functions in our example in the end of this paper.

(0, 0, 0, 0,-μ).

Whenμ=0, we getφ(0+)=0.On the other hand, by the definition ofφ(τ), we have

Thus, for the case thata<2c2(resp.a>2c2), functionφ(τ)has a unique positive zero in a small neighborhood of 0 when 0<μ1(resp.-1μ<0)and this zero tends to 0 asμ→0.Moreover, according to expressions ofg1(τ),g2(τ)given in(4), we have

This implies that this zero is in Ω(c,a)for|μ|1.Therefore,by Theorem 1.1 there exists a unique CLC corresponding to this zero and this CLC births from a 1-degenerate two-fold whenμchanges from 0 to a positive(resp.negative)number.

To end this paper, we take some values forcandμin system(3)as examples.Whenc= 1/3 andμ=-0.1, we get Fig.3, where

Here, the curve Γ1(resp.Γ2)has a horizontal asymptotic linea= 27/4(resp.a=9)asa→+∞(resp.a→-∞).The curves Γ1and Γ2intersect at point(a,τ)=(0,27).This is consistent with the analysis in the first paragraph of this section.

For a fixeda, set Ω(c,a)is the segment below curves Γ1and Γ2and above lineτ=0.From Fig.3, we obtain that there exists no CLCs, one CLC, two CLCs whena∈(-∞,0.31),a∈{0.31}∪[0.34,+∞),a∈(0.31,0.34)respectively.

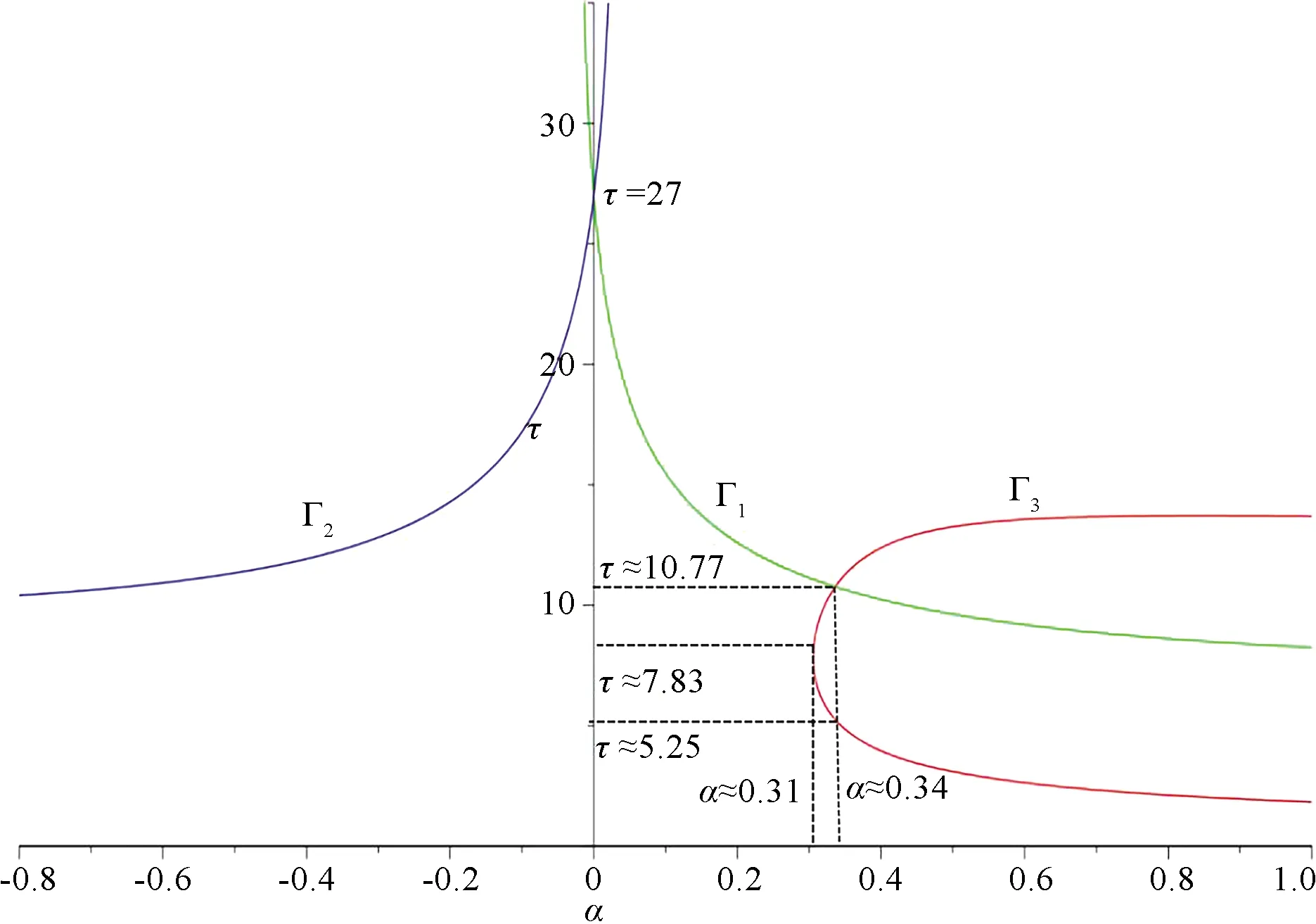
Fig.3 Domain Ω(c,a) and zeros of φ(τ)in(a,τ)plane of system(3)when c=1/3, μ=-0.1

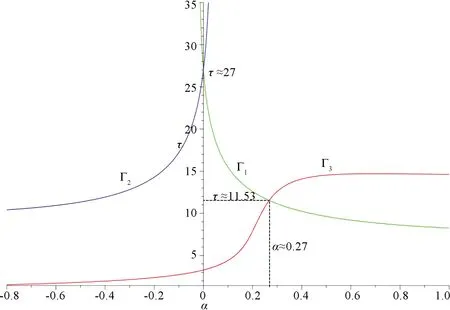
Fig.4 Domain Ω(c,a) and zeros of φ(τ)in(a,τ)plane of system(3)when c=1/3, μ=0.1

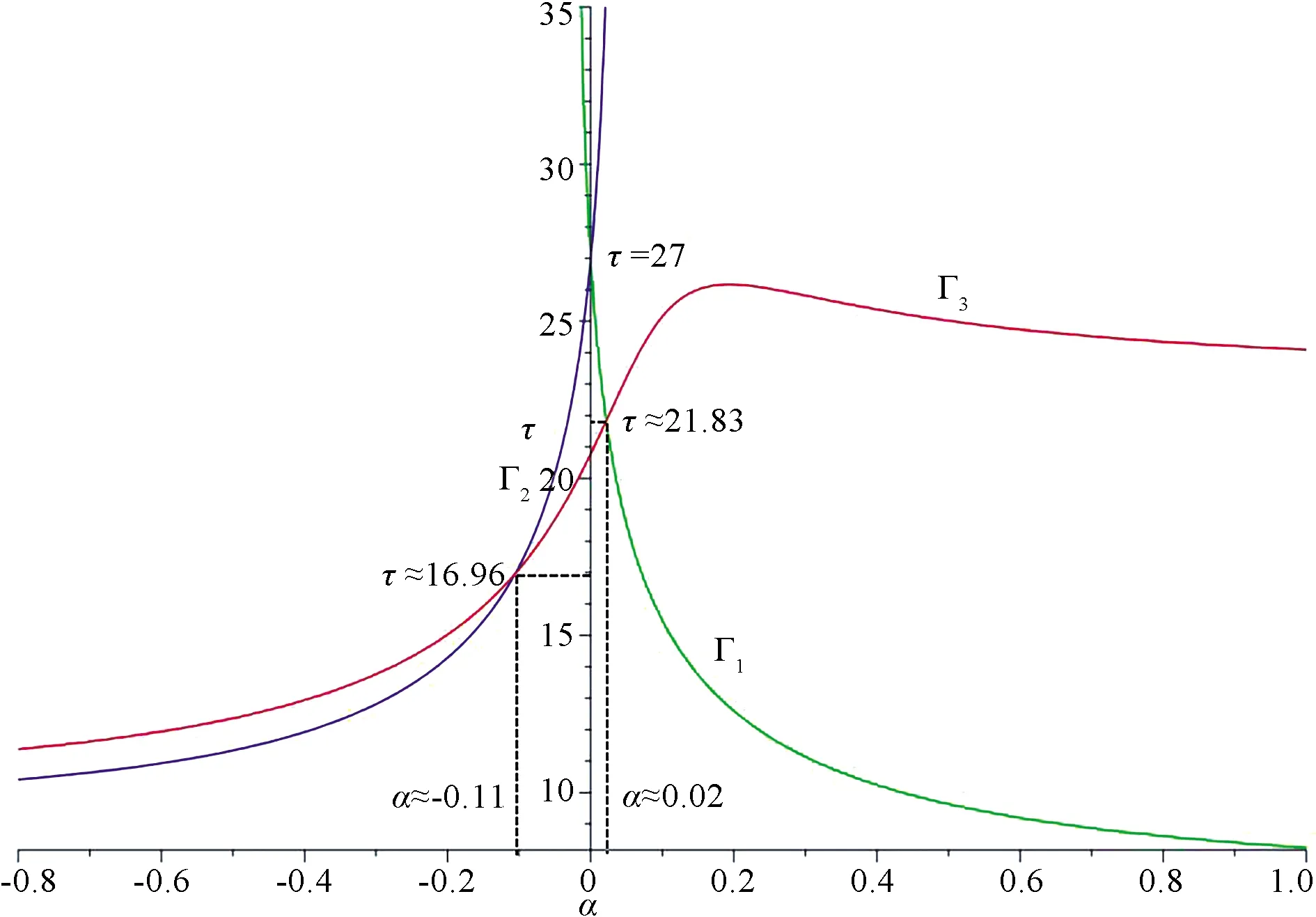
Fig.5 Domain Ω(c,a) and zeros of φ(τ)in(a,τ)plane of system(3)when c=1/3, μ=4

To observe more cases, we takec= 1/3 andμ= 0.1,μ= 4,μ= 7.5 in system(3)respectively and get Figs.4,5 and 6.One can obtain that there exists no CLCs, one CLC whena∈[0.27,+∞),a∈(-∞,0.27)in the case that(c,μ)=(1/3,0.1).There exists no CLCs, one CLC whena∈(-∞,-0.11]∪[0.02,+∞),a∈(-0.11,0.02)in the case that(c,μ)=(1/3,4).There exists no CLCs in the case that(c,μ)=(1/3,7.5).

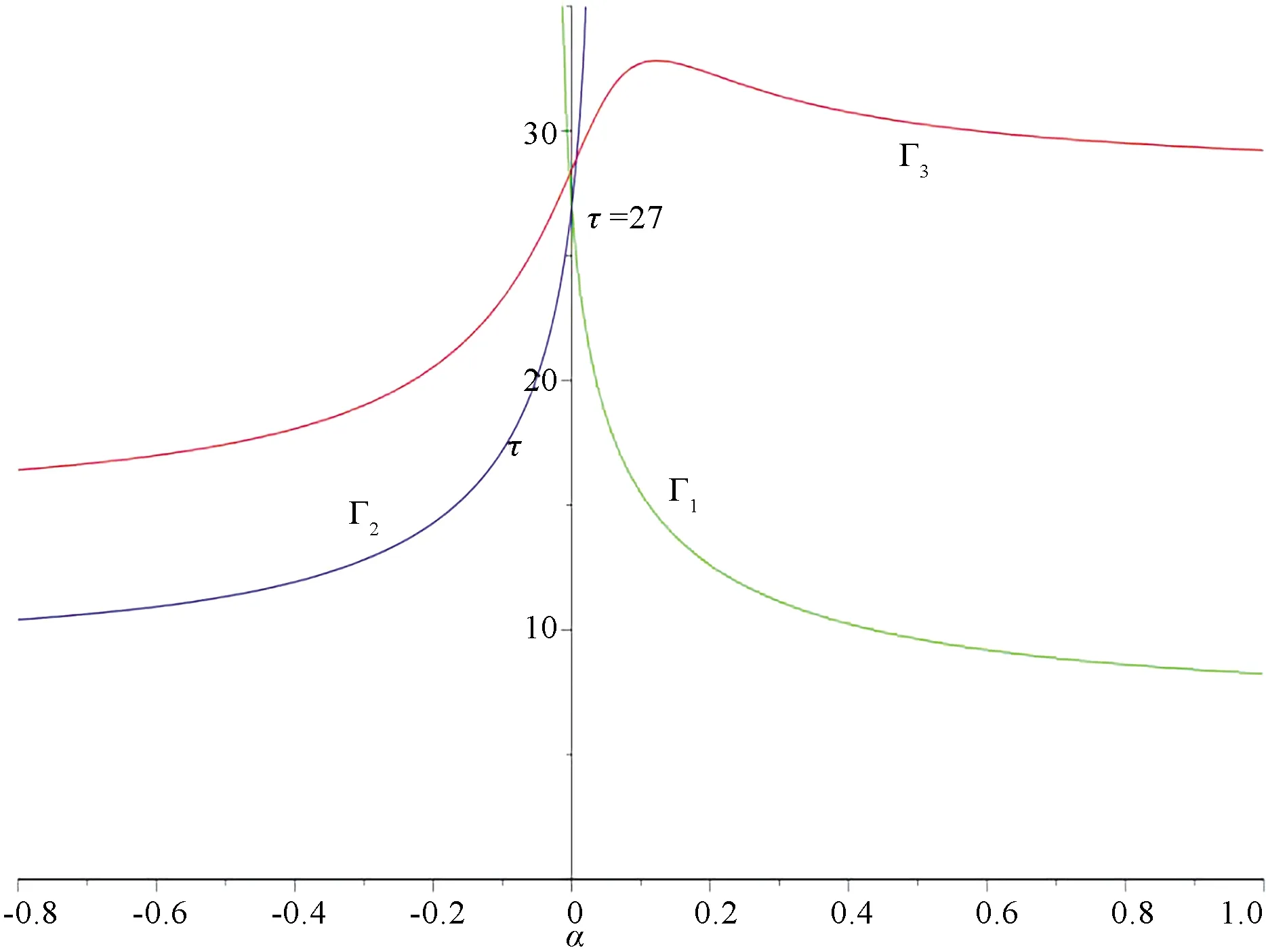
Fig.6 Domain Ω(c,a) and zeros of φ(τ)in(a,τ)plane of system(3)when c=1/3,μ=7.5