處理圓錐曲線問題的幾個關鍵點
安徽合肥市第九中學(230001) 殷春生
圓錐曲線問題是考查學生思維能力和計算能力的重要載體,在高考中常以壓軸題的形式出現。學生在解決此類問題時,常常因為方向不明確或思路不正確,致使解題有始無終。基于此,筆者提出處理此類問題需要把握的幾個關鍵點,并引例說明。
[例1]已知橢圓的離心率為,左、右頂點分別為A,B,點M是橢圓C上異于A,B的一點,直線AM與y軸交于點P。
(1)若點P在橢圓C的內部,求直線AM的斜率的取值范圍;
(2)設橢圓C的右焦點為F,點Q在y軸上,且AQ ∥BM,求證:∠PFQ為定值。
一、解題方向要準確無誤
定點、定值和最值問題是歷年高考重點考查的題型。本題第(2)問要求證明∠PFQ為定值,有些學生認為這個角可能為特殊角,如等,想到利用正弦定理、余弦定理等解三角形的有關知識求解,進而要求△PFQ的其他邊或角。因M是動點,所以點P、Q的位置不確定,要表示P、Q的坐標需要引入變量,再利用兩點間距離公式求邊長,即使可以表示出來,但不容易消元,計算煩瑣。
類似地,判斷一個角是銳角、鈍角、直角時,均可采用此種方法。
二、方法選擇要心中有數
圓錐曲線問題的求解思路,總的來說有兩種:一是引入直線方程,設出交點坐標,將其與曲線方程聯立,代入消元,結合判別式得出根與系數的關系,結合題目條件列出關系式,再代入根與系數的關系進行求解;二是采用設點法求解,即設出動點坐標(x0,y0),將其他相關點的坐標用x0,y0表示,再結合題目條件列出關于x0,y0的關系,最后將x0,y0代入曲線方程,據此進行消元處理。
本題中的動點是M,因M的變動,使得P、Q隨之變動,因此可采用設點法求解。具體解題過程如下:


本題在求解點Q的坐標時,也可利用直線BM與BQ的對稱性,即先求出直線BM與y軸的交點的坐標,再利用點Q與該點的對稱關系得出點Q的坐標。
三、隱含信息要挖掘清楚
本題能不能采用設直線的斜率k的方法來求解?答案是肯定的。這需要對題目中隱含的信息進行挖掘。本題中所隱含的信息在教材習題中有所體現。
[例2](人教版高中數學教材A 版選擇性必修1 練習)已知點B(6,0),C(-6,0),過點B的直線l和過點C的直線m相交于點A,設直線l的斜率為k1,直線m的斜率為k2,如果求點A的軌跡方程,并說明此軌跡是何種曲線。

此習題可推廣到一般的情況。
[例3]已知點B(-a,0),C(a,0)(a>0),過點B的直線l和過點C的直線m相交于點A,設直線l的斜率為k1,直線m的斜率為k2,如果求點A的軌跡方程,并說明此軌跡是何種曲線。
利用上述求解方法可得點A的軌跡方程為
對此結論進行逆向探究,可得出如下結論:
結論1已知橢圓的左、右頂點分別為A、B,M為橢圓上不同于A、B的一點,則直線AM、BM的斜率之積為定值

而例1 所給的條件,恰好符合這一結論,故可采用設直線斜率的方法求解。
例1 的另外解法:設直線MA的斜率為k,則直線MA的方程為y=k(x+2),令x=0,則y=2k,即點P(0,2k)。

教材中的例題、習題都具有典型性,其中隱含著重要的知識、結論,包括解題的方法。因此,廣大教師在教學中要尊重教材,充分利用教材,并引導學生主動探究教材,充分發揮教材的最大作用。
四、結論探究要進行徹底
上述結論也可以推廣到更為一般的形式,即只要A、B兩點關于坐標原點對稱,此結論仍然成立。
結論2已知橢圓A、B是橢圓C上關于原點對稱的兩點,M為橢圓上與點A、B不重合的一點,若直線AM、BM的斜率存在且不為0,則直線AM、BM的斜率之積為定值


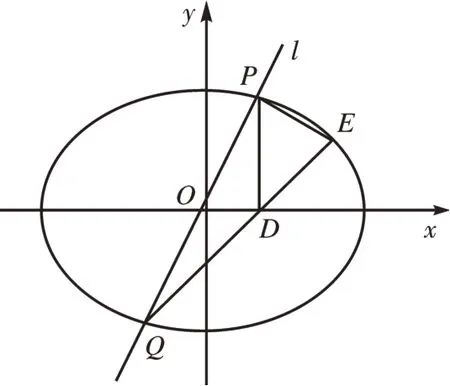
圖1
(1)求橢圓C的方程;
(2)直線l過坐標原點O,且不與x,y軸重合,交橢圓C于點P,Q,過點P作x軸的垂線,垂足為點D,連接QD并延長交橢圓C于點E,試判斷直線PE和l的斜率乘積是否為定值。若為定值,請求出該定值,否則請說明理由。


即PE和直線l的斜率之積為定值
本題中橢圓上的點P與點Q關于坐標原點對稱,所以直線PE與QE的斜率之積為定值。只要我們心中有這個結論,解題的方向也自然就明確了。
類似地,在雙曲線中也存在這一結論。

計算量大是圓錐曲線問題的重要特征,因此在解決圓錐曲線問題時除了要注意上述幾個關鍵點,還要做到準確計算。
總之,圓錐曲線問題雖然形式多變,方法靈活,但是只要我們能夠準確把握好關鍵點,就能以不變應萬變,順利、準確地解決問題。

