基于貝葉斯網絡的車用空氣彈簧智能測量與數值分析技術

馮帆

（陜西國防工業職業技術學院，陜西西安 710300）

空氣彈簧是各種類型汽車廣泛應用的空氣懸架，其通過充放氣實現懸架高度與強度的調整。由于空氣彈簧的有效面積存在非線性特征，對于空氣懸架的準確建模與分析具有較為重要的意義。

在對空氣彈簧的數據進行分析時，由于測試手段的局限性，且診斷對象具有較強的復雜性，通常導致測量結果不精確。在對于類似汽車空氣彈簧等復雜系統的研究中，存在著強耦合的相互作用，其數據分析與故障診斷是工業界的難點問題。

貝葉斯網絡是目前應用廣泛的不確定性知識表達與推理的理論模型[1]。其作為一種基于網絡結構的數學分析工具，適用于表述汽車空氣彈簧這類復雜性強、不確定性高的系統[2]。

該文重點研究了基于貝葉斯網絡與有限元分析法對于空氣彈簧的強度、疲勞壽命及可靠性進行的論證，并通過實驗驗證了該分析技術的有效性。

1 汽車空氣彈簧分析建模

重型商用車的三層拋物線形板簧的設計必須包括對其疲勞行為的研究，文中主要對其進行可視化建模計算。其彈簧在懸架系統上的建模和有限元劃分，如圖1 所示。

圖1 空氣彈簧建模

根據實際經驗可知，以下負載將對氣動板簧的結構完整性產生較大的影響：

1）由于直行行駛而產生的純垂直載荷。

2）由于制動同時發生的垂直與橫向載荷。

以上兩個載荷的最大值是相對于車輛的半有效載荷Fn表示的。直線行駛時的最大垂直負載Lv,max如下所示：

最大橫向力Fv,max和滿制動時的Fbr,max如下所示：

上式中，a、b、c為由實驗測得的相關系數。該文在建模中既考慮了由于最大垂直載荷引起的應力，又考慮了由于制動引起的應力。表1 為此次空氣板簧的設計載荷和幾何參數。

表1 空氣彈簧的載荷和幾何參數

使用式（4）和式（5）計算三層拋物線形板簧的最大應力和位移：

其中，σmax是彈簧上的最大應力（MPa），s是彈簧的位移（mm），F是施加的力（N），n是彈簧的層數，w是彈簧的寬度，L是彈簧的長度（mm），E是彈簧材料的彈性模量。

其空氣彈簧的理論載荷和位移圖，如圖2 所示。

圖2 理論載荷和位移圖

通過實驗測試可知，空氣彈簧的剛度k為39.6 N/m。在建立空氣彈簧形變分析公式的基礎上，對拋物線形板簧進行計算機輔助設計（CAD）建模，并進行有限元分析。

文中基于應力的確定性疲勞破壞準則，根據概率模型建立基于體積的概率疲勞失效模型，定義如下：

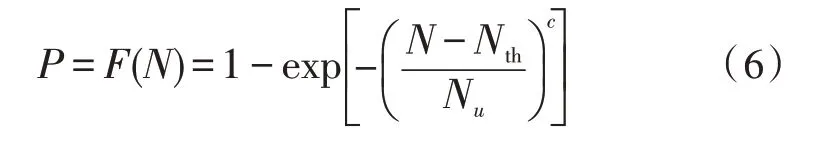
式中，Nu、Nth與c是彈簧應力變量S=Δσ的構成函數。

2 基于貝葉斯網絡的數值分析

為了進行數值分析，該文在CAD 模型中建立網格，即進行十六進制單元格分割。對于每個十六進制單元格，給定時間段內該網格獨立的事件數據。對于同屬于一個集合的兩個對象vij∈VALi，使用f(vij)函數來表征其出現的頻率，可建立式（7）對兩個對象之間的相似性進行評分[3-4]：

在建立相似性評分的基礎上，使用貝葉斯網絡建立數據分析平臺。文中使用3 種主要類型的層：卷積層[5]、池化層[6]和完全連接層[7]。卷積層與池化層是兩種類型的隱藏層[8]，類似于MLPN 中的隱藏層，完全連接層是常用的多層感知器網絡（MLPN）[9]。

此次設計的貝葉斯網絡框架，首先需要對彈簧的有限元模型中包含的3D 數據向二維矩陣投影。通過基于多個有限元模型比對，將相似的分類單元組織成樹狀結構來構建相似性信息的系統樹。式（7）所示的相似性由元素在樹中的緊密度來表示。在此次使用的系統樹中，假設樹中節點之間的距離恒定為1，通過任意兩個節點之間的節點數來定義其之間的距離。

在系統樹中，將CAD 樣本中每個屬性值分配給樹中的相應節點。填充完畢后，將節點的豐度轉換為二維矩陣。對于給定的行，選擇該行中節點的子級。并將豐度按照其父級出現的順序從最左列開始按順序放置在下一行中，矩陣的其余部分用零填充。

2.1 卷積層設計

與MLPN（1-D 格式）不同，卷積層與池化層中的所有內容均為2-D 格式[10]。在圖3 中，特征圖中的正方形代表MLPN 隱藏層中的神經元，內核中的正方形代表MLPN 中的權重值[11]。對該文的示例圖使用大小為3×3 的過濾器，該區域是高度與寬度均為3 的接收場[12]。

圖3 卷積運算流程

在輸入矩陣上對內核進行卷積時，通過卷積相似度函數找到特征圖的輸出。圖4 為此次特征圖的第一個通道操作清晰視圖。第一個過濾器在輸入的體積數據中查找某個特征，并生成自身的特征圖，以顯示該特征在原始圖像中的位置；第二個過濾器也將執行相同的操作[13]。

圖4 特征圖構建流程

由于卷積層并不維持空間分辨率，屬于有損操作[14]，因此步幅與濾鏡尺寸越大，損失的空間分辨率則越多[15]。該文則通過引入零填充，來保留原始輸入的空間分辨率。

每個神經元在兩種網絡類型中所進行的數學計算表示如下[16]：

1）通過使用代數點積作為相似函數，來發現MLPN 中每個神經元的輸出：

2）特征圖中每個神經元的卷積輸出表示為：

2.2 池化層設計

池化層用于減小特征圖的空間分辨率，進行池化操作雖然會引起參數數量的急劇減少，但同時也減少了模型過度擬合的風險，在保留重要信息的同時降低了維度。此次選擇一個窗口大小與一個步幅值作為單獨的圖層，并執行池化層操作。圖5 顯示了使用3×3 的窗口大小與跨度為3 時的最大池化操作。

圖5 功能圖上的池化操作

對于特征圖中的每個3×3 接收場區域，僅取最大值。生成的特征圖中顏色與執行合并的輸入特征圖中的接收字段相對應，因此特征圖的空間分辨率從9×9 降至3×3。

3 實驗驗證

為確保此次設計的數值分析平臺的可靠性，通過實驗進行驗證。

為達到分析平臺的最佳性能，需要對網絡進行詳細的設置。此次選取使用梯度下降的反向傳播算法作為學習算法，定義對數損失為成本函數。權重衰減衡量指標選為L2 范數，學習率設置為0.001，動量設置為0.9。體系結構設置為1 024 個輸入神經元，其中包括1 個包含了100 個神經元的隱藏層以及26 個輸出神經元。網絡訓練精度實驗如表2 所示。

表2 網絡訓練精度實驗

從表2 可知，文中設計的數據分析平臺在給定的時期內已成功收斂，并實現了較高的精度。為達到最佳實驗效果，此次嘗試了不同的體系結構以提高性能，包括更多的隱藏層以及增加或減少的層內神經元數量。通過實驗可以發現，在一個隱藏層中使用100 個神經元可獲得最佳結果（兩個數據集均約為30%）。與多層感知器數據分析平臺相比，文中使用的貝葉斯網絡數據分析平臺只需要極少的時間就可以收斂到局部或全局最小值。這意味著所需要的遍歷數據操作次數更少，即提高了數據平臺的分析效率。

使用該文建立的分析平臺對空氣彈簧進行疲勞測試與數據分析。執行器在測試元件中部施加負載，使用正弦力信號以恒定的測試頻率執行100 000次疲勞測試。表3 中顯示了樣品上最大負載情況下的最大應力與位移量。

表3 最大應力和位移值

根據實驗結果可知，對有限元分析與物理測試的結果進行了比較。結果比較表明，有限元分析是確定拋物線形板簧疲勞性能的一種合適而有效的方法。經過驗證，有限元結果的最大差異為0.91%。

表3 中，在設計負載情況下，計算最大應力為465 MPa，最大形變為109 mm。對于最大載荷情況下，計算最大應力為775 MPa，最大形變為190 mm。

如表4所示，分析計算出的疲勞壽命為181 540個循環。而實驗獲得的最小疲勞壽命為162 180 個循環，且實驗獲得的平均疲勞壽命為176 125 個循環。

表4 疲勞壽命分析結果比較

對于靜態分析結果，其數值分析的結果與實驗結果如表5 所示。

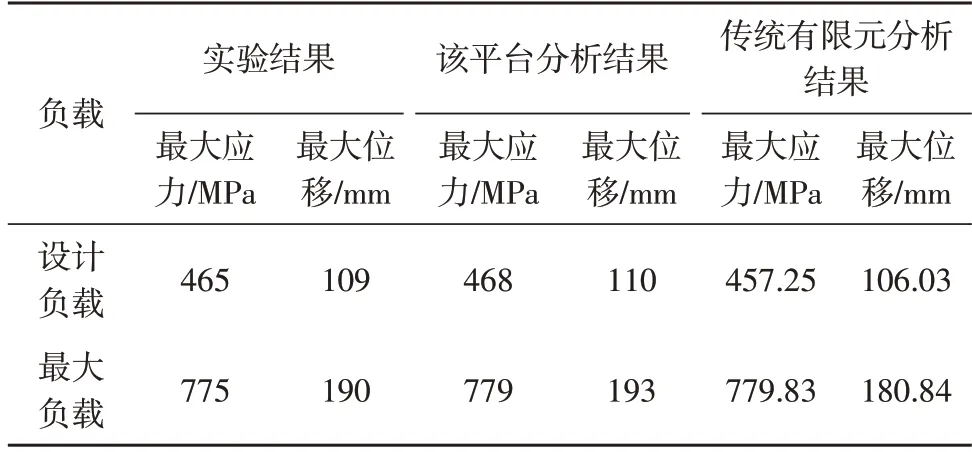
表5 最大應力與最大位移分析

通過對該文所提數值分析方法、傳統有限元分析法、實驗方法這3種方法的比較，這些方法獲得的結果彼此接近，且這些方法能夠用作彼此的替代方法。因此，所提方法對于空氣彈簧的數值分析均是可靠的。

4 結束語

該文使用貝葉斯網絡與有限元分析法，對汽車懸架系統中的空氣彈簧進行了建模與分析，可得出以下結論：

1）對于靜態最大應力，傳統有限元分析結果比實驗結果高2.29%，而該文所提平臺的分析結果僅比實驗結果高1.66%。

2）根據疲勞測試結果進行的可靠性分析表明，該平臺以99%的概率獲得100 000 個周期的期望壽命周期，能夠保證空氣彈簧在汽車的服務期內安全使用。

在今后的研究中，如何使用文中建立的平臺并提高數據分析的效率，將是今后的重點研究方向。