儲氣庫注采井井筒溫度場預測與影響因素分析

王建軍， 曾祥俊， 賈善坡， 隋曉鳳， 張赟新， 賀海軍

(1.中國石油集團工程材料研究院有限公司/石油管材及裝備材料服役行為與結構安全國家重點實驗室， 西安 710077; 2.東北石油大學地球科學學院， 大慶 163318; 3.東北石油大學非常規油氣研究院， 大慶 163318; 4.東北石油大學土木建筑工程學院， 大慶 163318; 5. 中國石油新疆油田分公司呼圖壁儲氣庫作業區， 昌吉 831200; 6.中國石油大慶油田有限責任公司采油工程研究院， 大慶 163453)

地下儲氣庫注采井井筒是保證天然氣注入、采出的安全通道，注采井受力與變形的影響因素不僅包括重力、浮力、管內外流體壓力、底部封隔器處約束方式、操作順序等常規外界因素，還需要考慮注采井井筒溫度、壓力非線性分布、注采交變荷載、溫度及腐蝕對井筒結構強度影響。由于一般儲氣庫井設計壽命在30年以上，運行時間較長，因此要確保井筒在設計年限內安全使用，必須對引起井筒結構破壞的因素進行深入研究，否則會出現注采井泄露、水泥環內部產生微裂隙或膠結面密封失效等問題[1]。從國內已建成的大港儲氣庫群、京58儲氣庫群等儲氣庫井筒泄露問題來看，主要是由于因交變荷載變化過大，超過接頭額定承載能力，密封性不足而引起的泄漏，注采氣溫度交替變化是產生過大載荷的主要因素。所有的地下儲氣庫注采井的井筒都將面臨注采過程中溫度的周期性變化，準確簡便地預測井筒內溫度分布，對于儲氣庫的安全運行至關重要。

目前，獲得井筒溫度、壓力等數據的方法是通過下入井下壓力計和溫度計對井筒溫度和壓力的沿程分布進行動態監測，但是該方法成本較高，并且下放的儀器有使用條件的限制，對于一些高溫高壓氣井來說并不適用。此外，就是通過數值模擬的方法和建模解析的方法對井筒溫度和壓力進行預測。國內外學者開展了大量關于井筒溫度和壓力預測的理論研究，迄今運用最為廣泛的是Ramey[2]建立的井筒熱傳導理論模型，分析了單相不可壓縮流體和理想氣體在注入井內溫度分布情況，模型中假設井筒內熱量傳遞為穩態過程，在地層的熱量傳遞為非穩態過程，將井筒內油管、環空、套管和水泥環等結構組成的多個熱阻用總傳熱系數來表示，熱量在地層的傳遞比較復雜，引入了無因次時間函數用來表征地層的非穩態傳熱過程，極大簡化的計算過程，并且證明了該模型的適用性。之后的研究者認為模型中井筒的總傳熱系數不能當作常數考慮，對環空部分流體的對流傳熱系數和輻射傳熱系數進行了討論，并且根據現場測溫資料回歸出了模型中松弛距離的統計公式，進一步簡化了井筒溫度的計算過程[3-6]。為了使井筒溫度模型適用范圍更廣，Hasan等[7]將兩相流引入的溫度模型之中，分析了Joule-Thomson效應對井筒溫度的影響，對無因次時間函數進行的分段處理，提高了熱量在地層中非穩態傳熱的計算精度，對于井筒壓力分布，運用最為廣泛的是Culldener-Smith采用的分段迭代的方法求解。因此，對溫度和壓力預測的方法主要分為三類：第一類，利用Ramey經典的傳熱模型，該模型將壓力剝離出來，并且沒有考慮流體的摩擦和動能改變項對井筒溫度分布的影響，認為井筒內氣體為理想氣體，與實際生產情況相差較大。但該模型解析表達式計算簡單，可以簡便地計算出井筒任意深度處流體溫度。第二類，通過分段平均的方式對井筒壓力分布進行迭代計算，這種計算方法需要對壓差進行分段，按長度增量迭代或者對長度分段，按壓力增量進行迭代，計算出劃分管段的平均壓力和平均溫度。第三類，利用質量守恒定律、能量守恒定律和動力定理，將溫度和壓力進行耦合計算[8]。部分學者利用以上方法對井筒注入或采出某單一過程的流體溫度和壓力進行預測，對于地下儲氣庫而言，在生產周期內，包括了注采過程、采氣過程和關井階段，對符合儲氣庫注采規律的溫度和壓力預測的研究較少。

根據地下儲氣庫實際生產運行規律，對溫度、壓力預測的方法進行優化，推導出符合地下儲氣庫注采全過程的溫度、壓力預測方法。本文利用顯式四階Runge-Kutta數值求解方法[9]，將溫度、壓力、密度和流速等流動參數進行耦合計算，以井底或者井口處氣體流動參數為初值，利用單步遞推的計算方式輸出注/采氣過程中溫度、壓力等氣體流動參數的沿程分布數據。為了系統的分析注采井井筒的溫度分布，現根據地下儲氣庫實際生產情況，把注采井井筒運行過程分為開井階段和關井階段，在關井階段，以關井前一刻氣體流動參數作為計算關井后溫度變化的初值，以得到關井后油管內氣體溫度的沿程分布情況。

1 儲氣庫注采井井筒溫度場預測模型

儲氣庫在生產周期內主要分為開井階段和關井階段，在開井階段注/采氣過程中井筒內氣體會持續不斷的注入或者采出。從而假設出氣體在井筒內作一維穩定流動，即油管內氣體的流動參數不隨時間變化，只在流動方向上發生變化，油管內任意截面處流動參數均勻。

為了更為簡便和精確地預測各階段油管內氣體溫度，以垂直井為例，做出如下假設：①油管內氣體到水泥環外緣的傳熱過程為穩態傳熱，熱量在地層間為非穩態傳熱；②熱量以導熱形式從油管傳遞到地層，徑向傳熱量遠大于縱向傳熱量；③油管、套管和水泥環為同心圓；④關井后，油管內氣體由運動變為靜止，忽略續流的影響。計算模型如圖1所示。

根據圖1所示的井身結構，對取出的單元控制體進行徑向傳熱、開/關井階段的傳熱分析。在徑向傳熱分析中，認為熱量在油管、環空、套管和水泥環這部分做穩定傳熱，將這部分考慮為由單一熱阻構成的傳熱介質[10]，引入總傳熱系數Uto來表征熱量在穩態傳熱區的傳遞；熱量在地層間做非穩態傳熱，將地層的熱阻考慮為與時間有關的函數關系，引入無因次時間函數來表征熱阻隨時間的變化，簡化了熱量在地層之間的非穩態傳熱。對于開井階段，根據儲氣庫實際生產時的規律，結合流體力學中質量守恒定律、能力守恒定律和動量定理，認為天然氣在注采井油管內做一維穩定流動，考慮氣體的壓縮性，通過Runge-Kutta單步遞推的數值求解方法，得到了密度、流速、溫度和壓力的沿程分布情況。在關井階段，氣體速度的穩定比溫度的穩定要快得多，認為關井后氣體停止運動，以關井前劃分井段的溫度和密度為計算初值，得到關井后溫度的沿程變化情況。

圖1 傳熱模型示意圖Fig.1 Schematic diagram of the heat transfer model

1.1 徑向傳熱

油管內氣體到地層的傳熱過程為氣體與油管內表面的對流傳熱、油管導熱、環空部分對流傳熱和輻射傳熱、套管導熱、水泥環到地層的導熱，徑向傳熱模型如圖2所示。

根據假設條件①，油管內氣體到水泥環外緣認為由單一熱阻構成的穩態傳熱，傳遞的熱量[11]為

dQ1=2πrtiUto(Tf-Th)dz

(1)

式(1)中：Uto為總傳熱系數，W/(m·℃)；dQ1為井筒單位時間內dz長度上的熱損失，W。

水泥環外緣到地層的傳熱過程為非穩態傳熱，引入無因次時間函數[11]，則傳遞的熱量為

rti為油管內半徑，m；rto為油管外半徑，m；rci為套管內半徑，m；rco為套管外半徑，m；rh為水泥環半徑，m；Tf為油管內氣體溫度，℃；Tan為環空保護液溫度，℃；Tci為套管溫度，℃；Th為水泥環外緣溫度，℃；dz為取出的單元控制體長度，m圖2 徑向傳熱示意圖Fig.2 Radial heat transfer schematic

(2)

式(2)中：ke為地層導熱系數，W/(m·℃)；Te為地層溫度，℃；dQ2為地層單位時間內dz長度上的熱損失，W；f(td)為無因次時間函數，無量綱。

無因次時間函數的公式為

(3)

(4)

式中：α為地層熱擴散系數，m2/s;t為生產時間，s。

由于油管內氣體傳遞的水泥環外緣的熱量等于水泥環外緣向地層傳遞的熱量，則水泥環外緣溫度[12]為

(5)

套管內表面溫度[12]為

(6)

式(6)中：kcem為水泥環導熱系數，W/(m·℃)。

由于油管的導熱性能良好，使得油管內氣體溫度與油管外表面溫度差異很小，則環空部分溫度[12]近似

(7)

總傳熱系數為

(8)

式(8)中：ktub為油管導熱系數，W/(m·℃)；hr為環空內輻射傳熱系數，W/(s·m2·℃)；hc為環空內對流傳熱系數，W/(s·m2·℃)；kcas為套管導熱系數，W/( m·℃)。

1.2 開井階段

以垂直井為例，氣體在油管內作一維穩定流動，規定坐標軸正向與氣體流動方向一致，取dz長度的管段為單元控制體，如圖3所示。

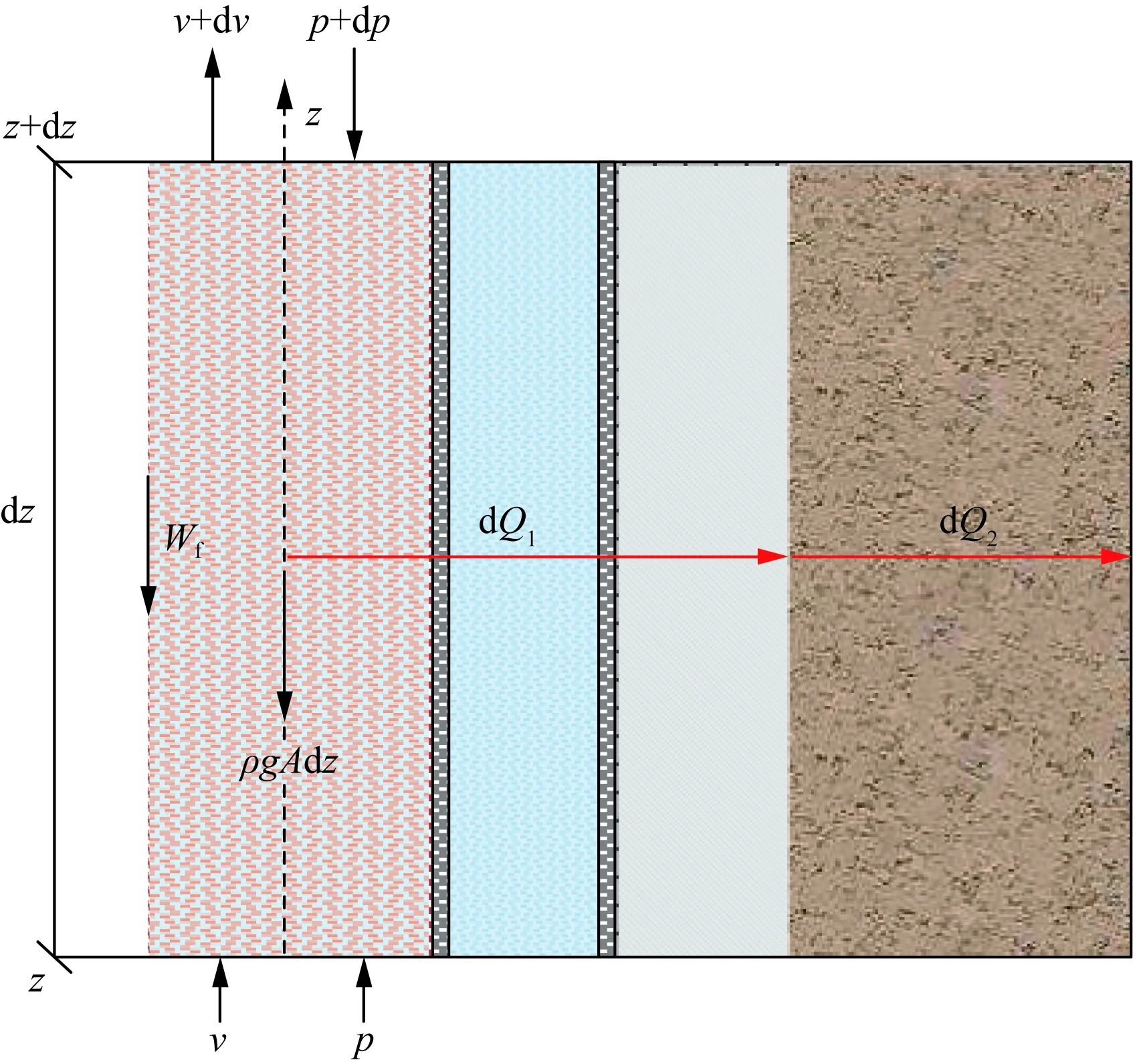
ρ為氣體真實密度，kg/m3；ν為氣體流速，m/s；A為油管截面積，m2；g為9.8 m/s2；Wf為摩阻力，N 圖3 開井階段單元控制體示意圖Fig.3 Schematic diagram of the unit control body in the well opening stage

根據流體在油管內做一維流動假設，流動參數只在流動方向上發生變化，油管內任意截面處流體參數均勻，由質量守恒定律得到單位時間內流入單元體的質量等于流出單元體的質量，則微分形式的連續方程[13]為

(9)

根據動量定理，則壓力梯度[10]為

(10)

式(10)中：f為管壁摩擦系數，無量綱。

根據能量守恒定律[10]：

(11)

式(11)中：h為氣體比焓，J/kg；q為單位質量氣體熱損失，J/kg。

井筒內為穩態傳熱，井筒與地層之間為非穩態傳熱[13]，由dQ1=dQ2，可得

(12)

式(12)中：ω為質量流量，kg/s。

流體比焓為

(13)

式(13)中：CJ為Joule-Thomson系數，K/Pa。

由于油管管徑變化很小，故Joule-Thomson系數甚小可以忽略，根據式(11)～式(13)，則溫度梯度[14]為

(14)

引入松弛距離L為

(15)

氣體密度根據實際氣體狀態方程得到在深度方向上微分形式[13]為

(16)

式(16)中：M為氣體摩爾質量，kg/mol；R為氣體常數，R=8.314 J/(mol·K)；Z為壓縮因子，無量綱；T為熱力學溫度，K。

根據式(9)、式(10)、式(14)和式(16)，分別得出注氣過程[式(17)]和采氣過程[式(18)]中溫度梯度、壓力梯度、密度梯度、速度梯度的微分方程組[8-9，13]為

(17)

(18)

式(18)中：Cp為天然氣定壓比熱。

Cp=1 243+3.14T+7.931×104T2-

6.881×107T3

(19)

油管內任意溫度和壓力條件下，氣體密度和氣體流速[14]為

(20)

(21)

式中：γg為氣體相對密度；P為氣體壓力，MPa；qsc為標準狀態下氣體流量，m3/d。

天然氣與油管內壁的摩擦系數f的計算公式為

(22)

式(22)中：ε為管壁的絕對粗糙度，mm；Re為雷諾數，無量綱。

將密度梯度、速度梯度、壓力梯度、溫度梯度分別記為Fi(i=1，2，3，4)初始條件記為井口或井底處密度、速度、壓力、溫度，步長記為x。

(23)

利用經典的四階Runge-Kutta求解此方程組，計算過程[9，13]如下：

(24)

(25)

以井口或者井底的流動參數為初值，通過顯式Runge-Kutta的數值求解方法依次計算，從而輸出任一深度處氣體的密度、流速、溫度、壓力等參數。

1.3 關井階段

關井之后，油管內充滿一定壓力和溫度的氣體，氣體由運動狀態變為靜止[15]，取長度為dz的單元控制體，如圖4所示。

圖4 關井階段單元控制體示意圖Fig.4 Schematic diagram of unit control body in shut-in stage

熱傳導損失于地層中的熱量等于內能的變化量加上井筒結構中吸收的熱量再減去單位長度控制體動能、勢能和焓變的改變量[16]，則能量平衡方程為

(26)

式(26)中：m為油管內氣體的質量，kg；m′為井筒結構的質量；E為氣體內能，J/kg；E′為井筒系統的內能，J/kg。

關井后，油管內氣體由運動狀態變為靜止，則質量流量為0，式(26)變為

(27)

井筒向地層吸收或損失的熱量為，則有

Q=Cp(Te-Tf)L′

(28)

式(28)中：L′為質量流量為0時的松弛距離[7]。

(29)

由于油管、套管、環空和水泥環吸收的能量和井筒內能量變化量存在比例關系為

CtmE=m′E′

(30)

(31)

式中：Ct為熱存儲系數[7]，在關井壓力恢復時取2，在壓力降低時取3。

氣體溫度關于時間和空間上的微分方程[7]為

(32)

在關井的初始時刻，，此時油管內氣體溫度Tf0等于關井前一刻油管內氣體溫度Tf，則關井階段氣體溫度關于時間的方程[7，15-16]為

(33)

(34)

1.4 計算流程

注采周期內油管內氣體流動參數計算流程[17-36]如圖5所示。

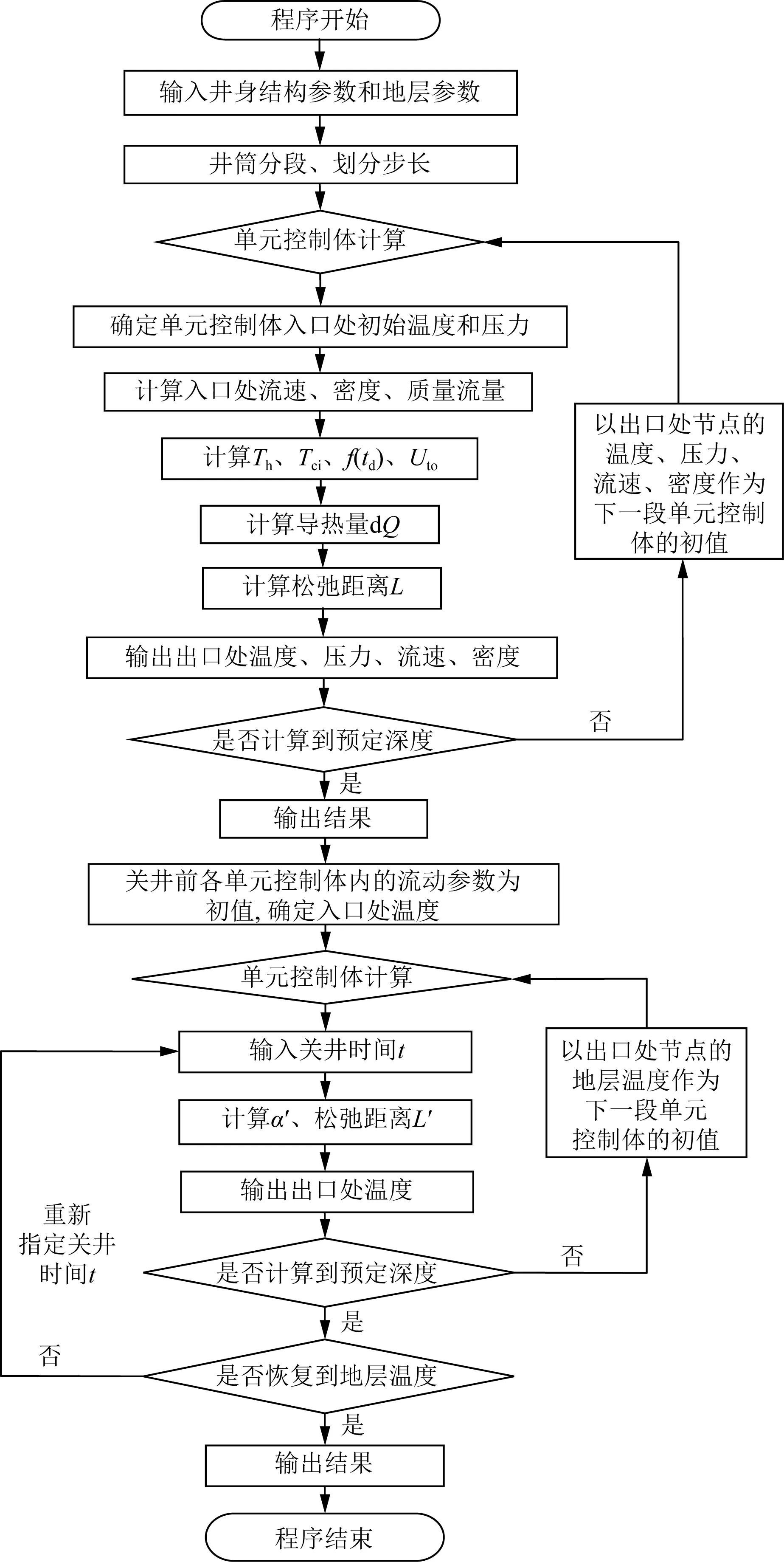
圖5 流動參數計算流程圖Fig.5 Flow parameter calculation flowchart

2 模型驗證

以ZS 8井注入CO2為例，CO2氣體受溫度和壓力影響，在不同井深處相態會發生改變，由液態轉變為超臨界狀態，達到超臨界態的CO2氣體具有液體的密度但又具有氣體的特性，由于儲氣庫注采的天然氣中甲烷含量相對較高，因此用此案例來驗證耦合微分方程組計算的準確性。ZS 8井井筒和地層參數、初始注入條件[17]如表1和表2所示。

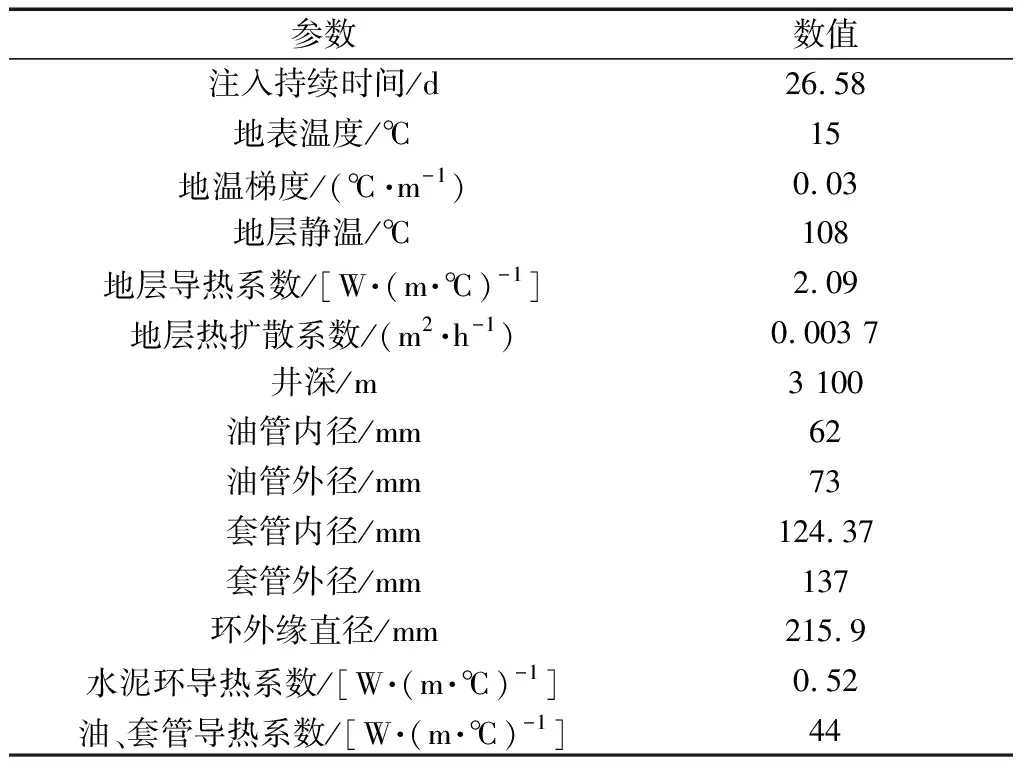
表1 ZS 8井井筒和地層參數表Table 1 Wellbore and formation parameters of well ZS 8

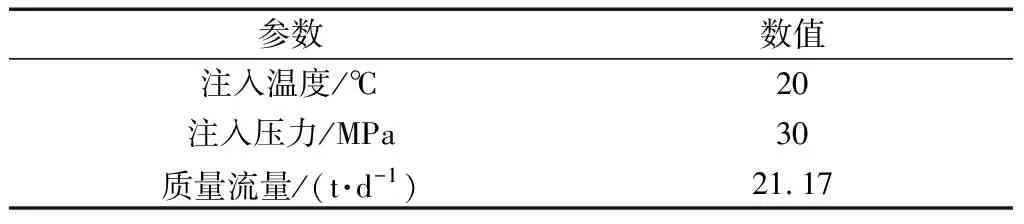
表2 CO2初始條件Table 2 CO2 initial conditions

根據圖6(a)和圖6(b)所示，CO2氣體溫度和壓力隨著深度的增加而逐漸升高，計算值與實測值趨勢一致，計算值略大于實測值，壓力計算值與實測值最大相對誤差為4.97%，溫度計算值與實測值最大相對誤差為3.18%，滿足工程實際要求。

3 儲氣庫注采井井筒溫度影響因素分析

以西部某儲氣庫X注采井為例，預測該井在注氣過程和采氣過程油管內氣體的溫度、壓力、流速和密度分布情況，并對不同注氣溫度、注氣壓力、注/采氣時間、注/采氣量等敏感性因素進行單因素分析，并且通過只考慮單元控制體徑向傳熱的假設條件下，井筒內環空溫度、套管溫度、水泥環溫度進行預測，以及關井階段，油管內氣體恢復到地層溫度所需時間進行分析，X注采直井井身結構如圖7所示。

X注采直井井筒和地層參數取值如表3所示。

圖6 ZS 8井氣體流動參數對比Fig.6 Comparison of gas flow parameters in well ZS 8

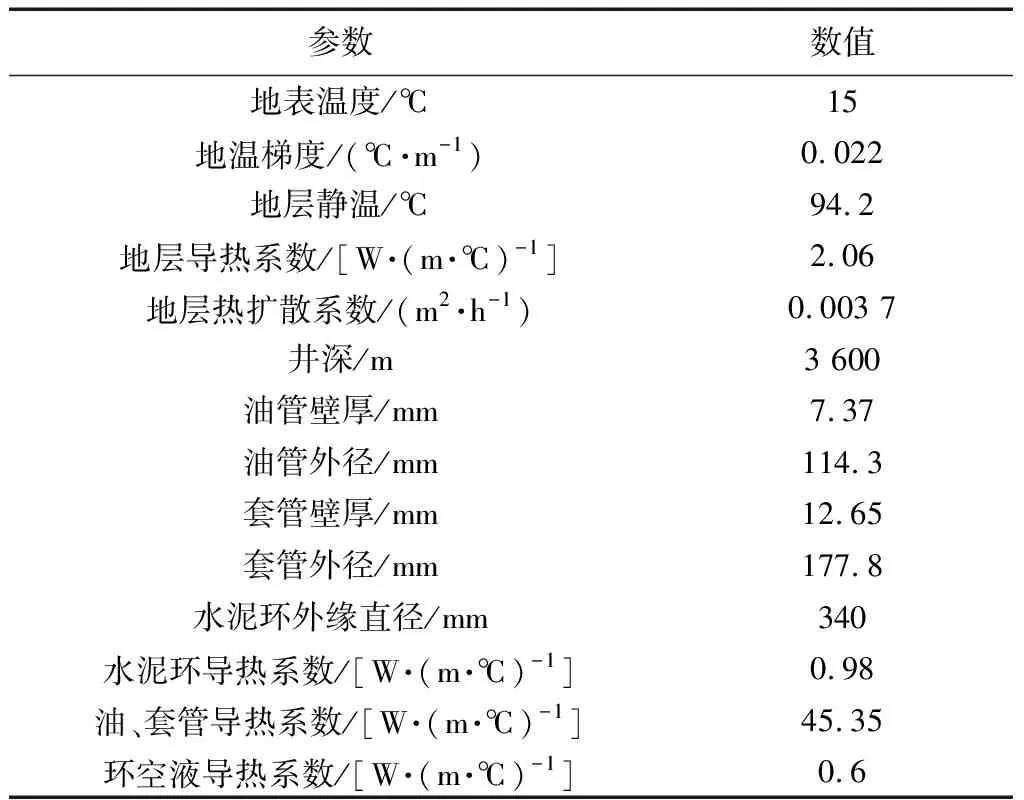
表3 X井井筒和地層參數表Table 3 Wellbore and formation parameters of well X

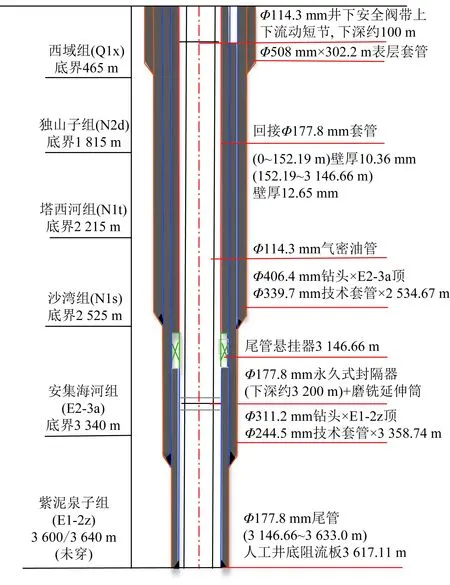
圖7 X注采直井井身結構示意圖Fig.7 Schematic diagram of the structure of the X injection-production vertical well

3.1 注氣過程

本階段以注氣時間為30 d，注氣壓力為30 MPa，注氣溫度為30 ℃時，注氣量為30×104、50×104、70×104、90×104、110×104m3/d時油管內氣體溫度、壓力、密度、流速的分布情況如圖8所示。

如圖8(a)所示，油管內氣體溫度隨深度增加而逐漸增大，這是由于隨著深度的增加，地層溫度逐漸高于注氣溫度，此時注入的氣體從地層中吸收熱量。在接近井口0～1 300 m范圍內，注氣量大時的氣體溫度高于注氣量小時的氣體溫度，其原因主要是注氣量越大，油管內氣體流速越快，如圖8(c)所示，油管內氣體與外界的熱交換就越小，注氣量越小，氣體流速越慢，與外界的熱交換就越大，在此范圍內油管內氣體溫度高于地層溫度，氣體與外界熱交換量相對較小。圖8(b)反映了隨著深度的增加，油管內氣體壓力逐漸增大，并且隨著注氣量的增大，油管內氣體壓力增大。其原因可根據圖8(d)可知，注氣量越大，油管內氣體密度越大，因而壓力增加，由密度方程[式(20)]可知，氣體密度又是關于氣體溫度和壓力有關的參數，因而相互影響。

注氣時間為30 d，注氣壓力為30 MPa，注氣量為50×104m3/d時，注氣溫度為20、30、40、50 ℃時油管內氣體流動參數分布情況如圖9所示。

圖8 注氣階段不同注氣量下氣體流動參數分布Fig.8 Distribution of gas flow parameters under different gas injection volumes during gas injection stage

圖9(a)反映了不同注氣溫度下，油管內氣體溫度沿程分布情況，在注氣溫度為20 ℃時，油管內氣體溫度呈現出隨深度增加而逐漸增大的趨勢，隨著注氣溫度的增大，油管內氣體溫度先出現了先降低后逐漸上升的趨勢。這是由于在接近井口處，隨著注氣溫度的增加，油管內氣體溫度與地層的溫差變大，導致散失的熱量增加。隨著深度的增加，不同注氣溫度之間的差異逐漸減小。圖9(b)反映了隨著注氣溫度的增加，油管內氣體壓力減小，可由圖9(c)可知，不同注入溫度條件下，油管內氣體密度不同，因而導致油管內氣體壓力出現變化。

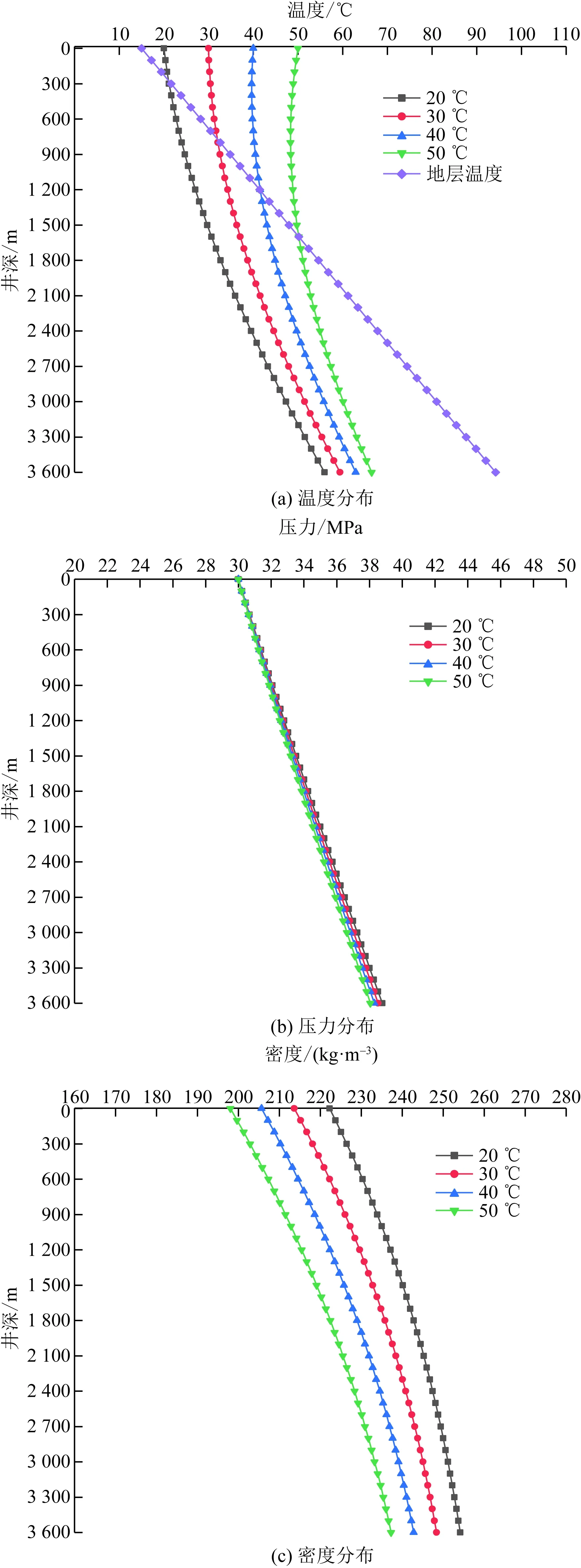
圖9 注氣階段不同注氣溫度下氣體流動參數分布Fig.9 Distribution of gas flow parameters at different gas injection temperatures during gas injection stage

注氣時間為30 d，注氣溫度為30 ℃，注氣量時50×104m3/d注氣壓力分為20、30、40 MPa情況下，油管內流體溫度和壓力變化情況如圖10所示。

圖10 注氣階段不同注氣壓力下氣體流動參數分布Fig.10 Distribution of gas flow parameters under different gas injection pressures during gas injection stage

圖10(a)反映出通過改變注氣時的壓力得到油管內氣體溫度沿程分布的情況，因此改變注氣壓力對于油管內氣體沿程溫度分布影響很小。圖10(b)反映了隨著注氣壓力的增加，油管內氣體壓力增大，可由圖10(c)可知，壓力增加，注入氣體的密度會顯著增加，隨著深度的增加，受到溫度增加的影響，氣體密度增加趨勢減緩。

注氣壓力為30 MPa，注氣溫度為30 ℃，注氣量為50×104m3/d時，注氣時間為10、30、50、70 d油管內氣體溫度分布如圖11所示。

圖11(a)反映出隨著注氣時間的增加，油管內氣體溫度降低不明顯，因此改變注氣量對油管內氣體溫度變化有顯著影響。則通過改變注氣量來影響井底溫度的效果優于改變注氣時間。

根據本文的模型假設，只考慮單元控制體徑向上的熱量傳遞，得到了注氣壓力30 MPa，注氣溫度30，注氣量為50×104m3/d時，注氣時間持續30 d，注氣階段井筒內套管、環空、水泥環外緣溫度預測。

圖11(b)反映出，在接近井口處，由于油管內氣體溫度高于地層溫度，則在0～800 m的范圍內油管內氣體溫度依次大于環空、套管和水泥環溫度，氣體溫度到套管溫度之間的差異較小；隨著深度的增加，地層溫度逐漸增大，在注氣30 d以及穩定注氣量的情況下，油管內氣體溫度到水泥環外緣的溫度依次升高，水泥環外緣溫度與線性變化的地層溫度之間存在差異，是由于在此注氣條件下，井筒的溫度對周圍地層存在一定的熱影響范圍。

圖11 不同注氣時間及井身結構溫度分布Fig.11 Different gas injection time and temperature distribution of well structure

3.2 采氣過程

圖12(a)反映出，隨著采氣量的增大，井口處氣體溫度顯著增加，越接近于井口處，不同采氣量之間溫度差異越大，主要原因是越接近于井口油管內氣體與地層的溫差越大，因而油管內氣體的熱量損失就會越大，并且采氣量的大小決定油管內氣體流速，由圖12(c)所示，隨著采氣量的增大，油管內氣體流速增加，導致溫度差異明顯。圖12(b)反映出隨著采氣量的增大，油管內氣體壓力逐漸降低，根據圖12(d)可知油管內氣體密度顯著下降，在采氣量較小時，氣體密度變化幅度較小，隨著采氣量的增加，密度變化較為明顯，加上加速度壓降損失和摩擦力損失會增大，因而導致油管內氣體壓力降低。

采氣壓力為33.96 MPa，地層溫度為94.2 ℃，采氣時間為30 d，采氣量為30×104、50×104、70×104、90×104、110×104m3/d時油管內氣體流動參數情況如圖13所示。

圖13(a)反映出采氣量為50×104m3/d時，采氣時間為10、30、50、70 d時油管內氣體溫度沿程分布清情況，油管內氣體溫度隨時間增加而增大，但增加的幅度較小，因而采氣時間的長短對油管內氣體溫度影響較小。

在采氣過程中，井底溫度比較高，因而油管內高溫氣體向井口流動的過程中向周圍地層傳遞熱量，因此，圖14(b)給出了采氣時間為30 d，采氣量為50×104m3/d時油管、套管、環空液、水泥環和地層的溫度沿程分布情況。根據圖13(b)可知，在此采氣工況下，井筒溫度對周圍地層的影響趨于穩定，油管溫度>環空液溫度>套管溫度>水泥環溫度>地層溫度，并且越接近于井口處，油管溫度與套管內表面徑向溫度差異越明顯。在油管內高溫氣體向周圍傳熱的過程中，環空液溫度升高，并受熱膨脹，套管軸向變形增加，會存在上抬井口的風險，環空液溫度發生變化，在溫度效應下又會產生環空壓力，因而通過本文的預測模型，計算出環空部分溫度，為計算環空壓力提供可靠的理論數據。

3.3 關井階段

計算了在采氣30 d，油管內氣體溫度、壓力、密度的分布情況，關井之后，以關井前氣體流動參數作為初始條件，此時油管內充滿一定溫度和壓力的氣體，氣體由運動狀態變為靜止，只存在徑向上的熱傳遞，則關井后，油管內氣體恢復到地層溫度的傳熱過程如圖14所示。

圖12 采氣階段不同采氣量下氣體流動參數分布Fig.12 Distribution of gas flow parameters under different gas production volumes in gas production stage

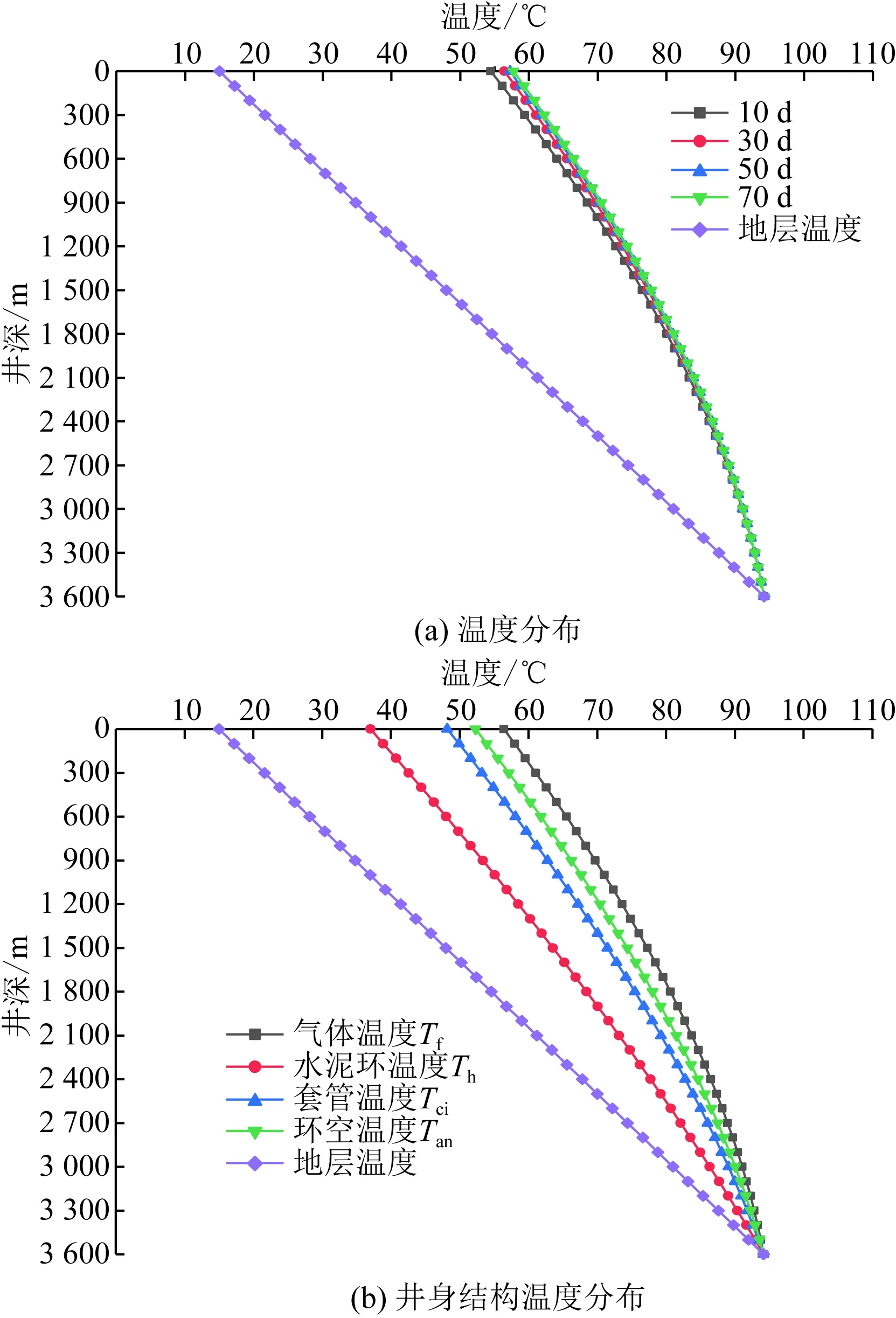
圖13 不同采氣時間及井身結構溫度分布Fig.13 Temperature distribution of different gas production time and well structure

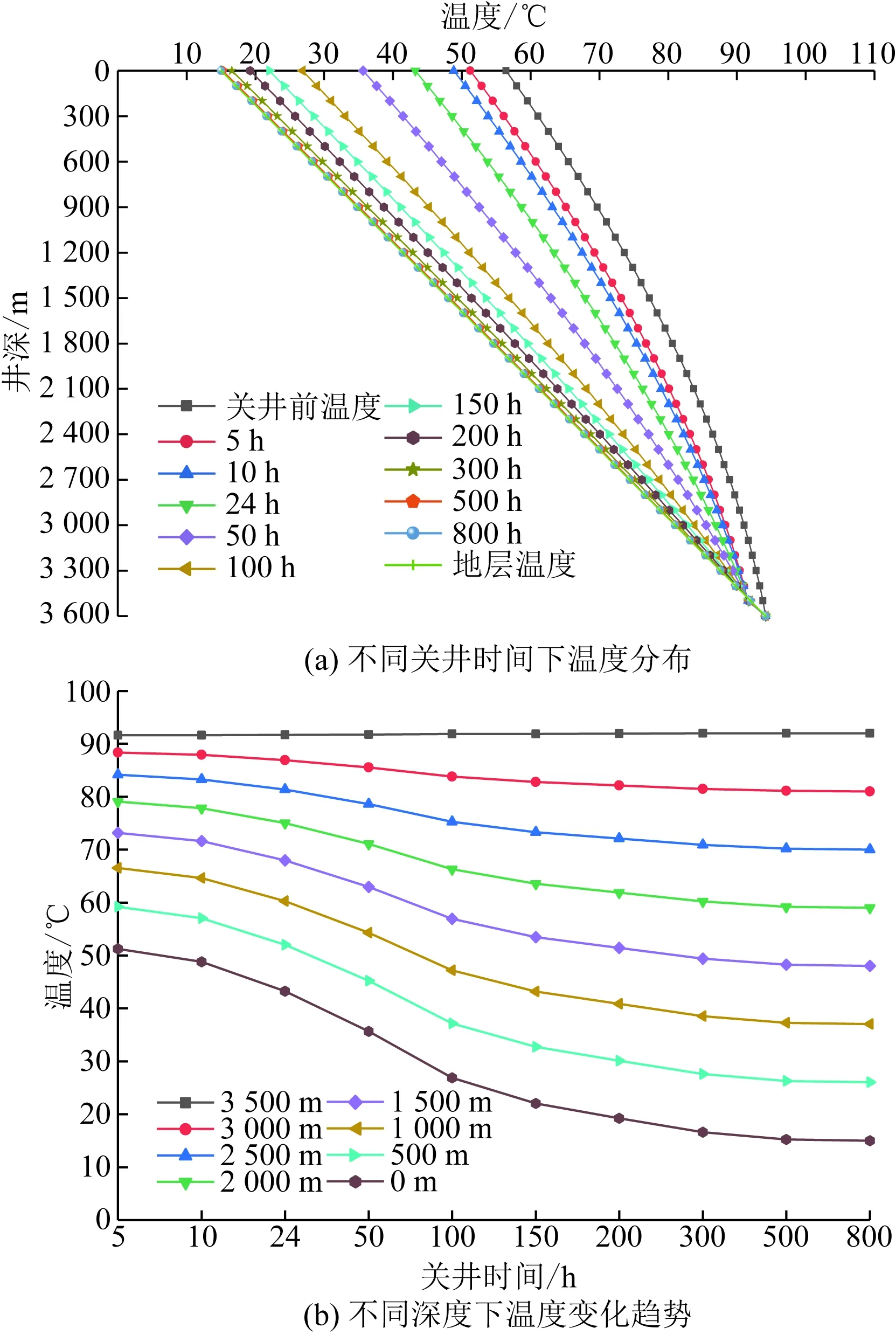
圖14 關井階段井筒分度分布Fig.14 Wellbore indexing distribution during shut-in stage

根據圖14(a)可知，隨著關井時間的持續增加，油管內氣體溫度會逐漸恢復至地層溫度，圖14(b)反映出，在關井初期，油管內氣體溫度下降速率較大，并且越接近于井口，氣體溫度下降速率越明顯，主要是油管內氣體溫度與地層溫差較大所致，隨著關井時間的持續增加，溫度變化速率逐漸放緩。隨著關井時間的持續增加，油管氣體溫度逐漸恢復至地層溫度。

4 實例分析

由于本文的計算模型需要以注氣時井口溫度或者采氣時井底溫度為初值對氣體流動參數的沿程分布情況進行求解，現場只能監測到井口處開井狀態下的溫度，因此引用西部某儲氣庫X注采井井筒采氣過程井口監測數據，計算出從2019年12月10日—2020年1月31日開井期間井口處氣體溫度，將預測值與實際監測的井口溫度進行比對，實測值與預測值如圖15所示，隨著采氣時間的持續增加，井口監測值呈現出上升趨勢，最大監測值為50 ℃，最小值為47 ℃。預測值高于實測值，計算溫度最高在56 ℃左右，分析誤差的來源可能為測量環境、模型中優化的井身結構與實際井身結構存在的差異、模型中的地層溫度為線性變化與實際存在差異、實際生產中產量不穩定、地層導熱率和地層熱擴散系數等因素引起誤差。通過對比可知，在該階段內，預測值與井口實際監測值吻合程度較高。說明本文所建立的溫度預測方法，適合于儲氣庫生產運行中的溫度預測。

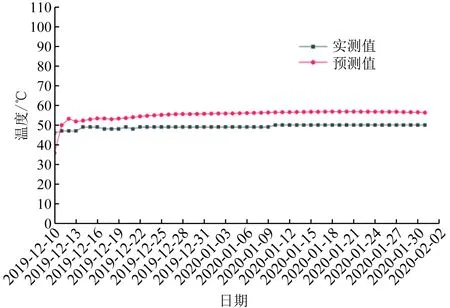
圖15 井口監測溫度與預測值對比Fig.15 Comparison of wellhead monitoring temperature and predicted value

5 結論

通過建立開井階段溫度梯度、壓力梯度、流速梯度和密度梯度耦合的微分方程組，利用Runge-Kutta數值求解方法，計算出不同深度處氣體的流動參數，并且考慮單元體徑向傳熱的假設條件下，得到了油管、環空液、套管、水泥環的溫度沿程分布情況，結合關井前氣體的流動參數，假設關井后氣體停止運動，得到了關井后不同深度處氣體恢復至地層溫度情況。綜上所述，得到以下結論。

(1)在注氣過程中，隨著注氣量的增大，井底處氣體溫度明顯降低，氣體壓力會隨著注氣量的增大而增加。注氣壓力和注氣量不變的情況下，改變井口處注氣溫度，發現接近于井底處，溫度之間的差異會逐漸縮小。井底處氣體溫度受注氣量的影響大于受注氣溫度的影響。

(2)隨著注氣時間的持續增加，井底處氣體溫度變化較小。只改變注氣壓力的大小，對油管內氣體沿程溫度的差異較小，但油管內氣體壓力會隨著注氣壓力的增大而增大。

(3)采氣階段油管內氣體溫度會隨著采氣量的增加而增大，但油管內氣體壓力隨著采氣量的增加而減小，因此在生產過程中要控制井口處壓力變化，可以通過改變采氣量的大小來控制壓力變化。

(4)在采氣量不變的條件下，隨著采氣時間的增加，井口處氣體溫度逐漸增加，但溫度增加幅度較小。

(5)關井階段，油管內氣體溫度會隨著關井時間的持續增加逐漸恢復至地層溫度，關井初期越接近井口處溫度變化速率越明顯，變化幅度越大。