基于有限元法的波紋曲梁結構振動特性研究

王京軍 邱 岳*

(1、中車青島四方機車車輛股份有限公司,山東 青島 266111 2、中車工業(yè)研究院(青島)有限公司,山東 青島 266071)

波紋曲梁結構作為一種典型工程結構零部件,具有輕質、高耐壓強度和變形小等優(yōu)點,廣泛應用于橋梁、交通運輸和船舶等工程領域。波紋曲梁結構的振動特性將嚴重由其組成整體結構振動性能,因此有必要對波紋曲梁結構開展振動特性分析,為波紋曲梁結構的結構優(yōu)化設計提供理論基礎。國內外許多學者已經(jīng)對波紋曲梁相關結構開展了深入研究,并取得了一系列成果。

寧曙東基于鐵木辛柯梁理論和歐拉- 伯努利方程,采用瑞麗- 里茲法開展曲率梁結構的面內自由振動特性研究[1]。趙雪健采用動剛度法研究平面曲梁結構的面內外振動特性,計算曲梁頻率和振型[2]。李星照等人基于歐拉- 伯努利梁理論,建立圓弧曲梁結構的自由振動微分方程,開展曲梁結構自由振動特性研究[3-4]。孫廣俊等人采用微分求積法建立曲線梁結構振動分析模型,研究曲線梁結構的振動特性[5]。葉康生等人采用p 型超收斂算法對平面曲梁面外自由振動問題進行求解[6]。謝臻等人基于Timoshenko 梁理論,采用無網(wǎng)格法和哈密爾頓原理,對曲梁結構開展自由和受迫振動特性分析[7]。陳明飛等人基于一階剪切變形理論,采用等幾何有限元法對變曲率功能梯度曲梁開展自由振動分析[8]。Ramon 等人基于薄厚曲梁理論,采用廣義/擴展有限元法對曲梁結構開展面內自由振動特性分析[9]。Samira 等人采用半解析法和有限元法對變截面復合曲線梁結構開展振動特性分析[10]。

綜上所述,現(xiàn)有研究主要是針對曲梁結構展開的,對波紋曲梁結構的研究較少。首先本文擬基于厚曲梁理論,采用有限元法和罰函數(shù)法建立一般邊界條件下波紋曲梁結構振動特性分析模型；緊接著確定懲罰因子取值并將本文模型求解結果與有限元軟件計算結果進行對比,開展模型驗證；最后對波紋曲梁結構振動分析模型開展參數(shù)化研究,研究幾何參數(shù)對波紋曲梁結構固有頻率的影響,為波紋曲梁結構優(yōu)化設計和減振降噪設計提高理論基礎和技術指導。

1 理論推導

1.1 波紋曲梁結構模型介紹

如圖1 所示,為波紋曲梁結構的幾何模型示意圖。波紋曲梁結構是由不同弧度曲梁結構通過共節(jié)點的方式耦合而成。圖1 中αi(i=1,2,3,4,5)表示曲梁結構的弧度角,且2α1=α2=α3=α4=2α5。為了方便起見,采用曲線坐標系zs 對曲梁結構進行描述,考慮三個方向的自由度,其中ui、wi和θi分別表示切向位移、徑向位移和轉角位移；曲梁結構的截面為矩形截面,b 和h 分別表示截面寬度和截面厚度；R 表示曲梁半徑。

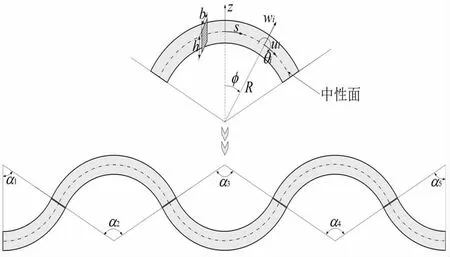
圖1 波紋曲梁結構示意圖

1.2 波紋曲梁結構模型建立

根據(jù)厚曲梁單元理論,曲梁結構上任意一點的應變與位移存在如下所示的線性關系：

式中εi、χi和γi分別表示拉伸應變、曲率變化和剪切應變。根據(jù)材料的本構方程,曲梁結構上任意一點應力和應變存在如下所示關系。

式中ρ 表示密度；Li表示曲梁結構弧長長度；“·”表示對時間t 的導數(shù)。根據(jù)有限元的基本理論,曲梁結構的位移場函數(shù)可以寫成如下形式：

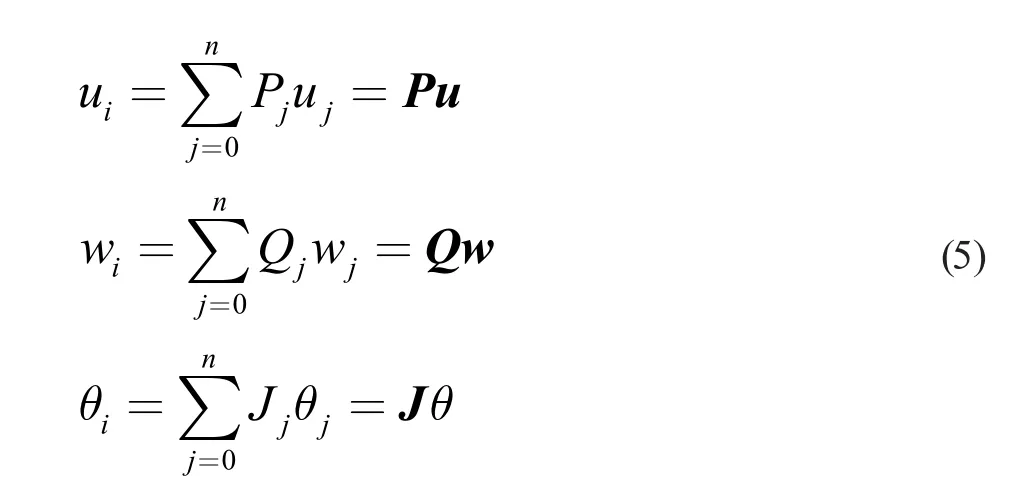
式中Pj、Qj和Jj分別表示與ui、wi和θi有關的位移形函數(shù),其具體表達式見文獻[9]；uj、wj和θj分別表示與ui、wi和θi有關的有限元節(jié)點自由度；n 表示單元節(jié)點個數(shù)；P、Q 和J 分別表示由位移形函數(shù)組成的矩陣。將式(1)、(2)、(3)和(5)帶入式(4)進行化簡可得。

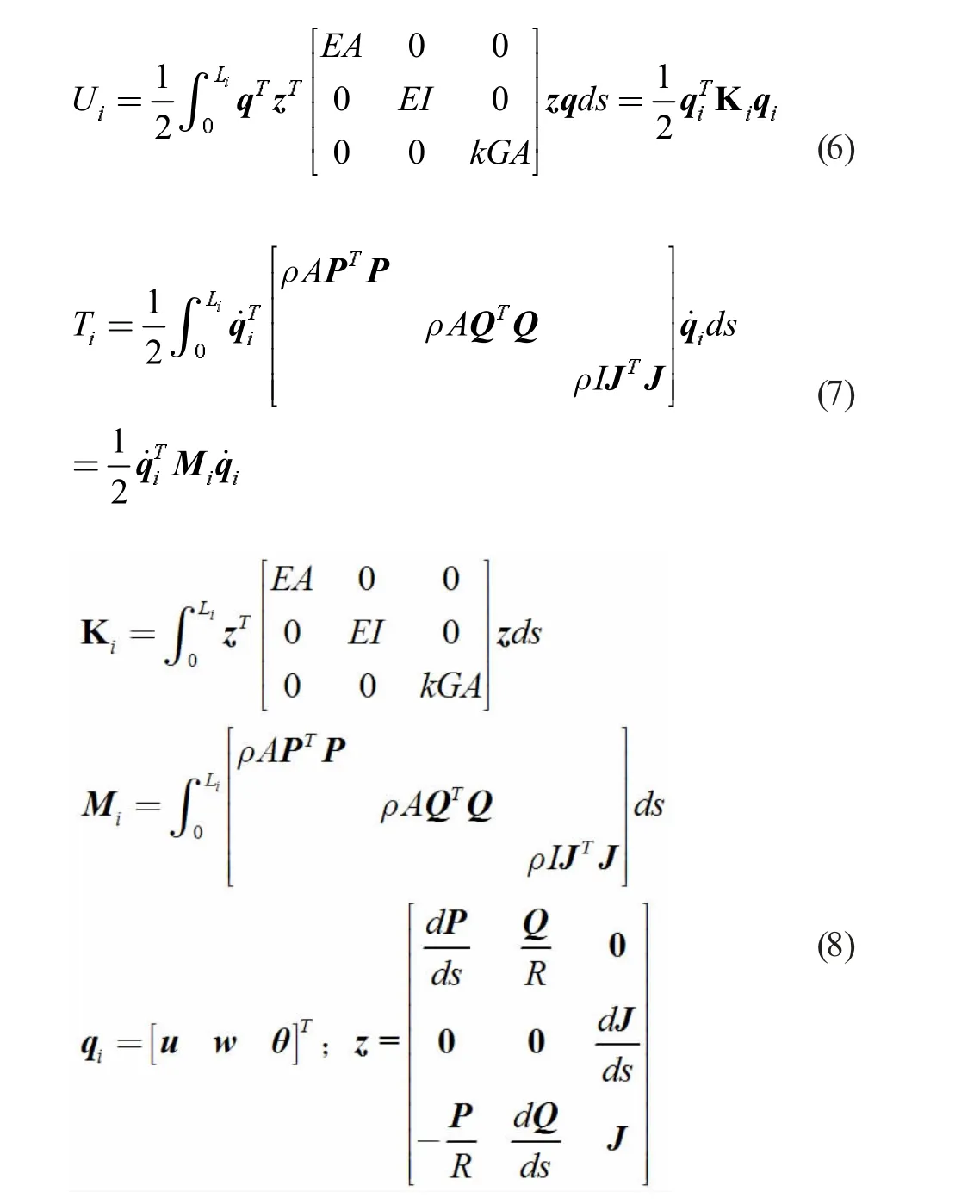
式中Ki和Mi分別表示曲梁結構的剛度矩陣和質量矩陣,qi表示曲梁結構有限元節(jié)點在各個自由度方向位移組成的列向量。由于波紋曲梁結構是由不同弧度的曲梁結構通過有限元共節(jié)點的形式耦合而成,所以波紋曲梁結構的整體剛度矩陣和質量矩陣可以通過不同弧度曲梁結構的剛度矩陣和質量矩陣累加得到。在進行累加之前,應當對曲梁結構的剛度矩陣和質量矩陣進行維度擴展,使得曲梁結構的矩陣維度和波紋曲梁結構的矩陣維度相同。波紋曲梁結構剛度矩陣和質量矩陣可以寫成如下形式：

式中S 表示懲罰因子,懲罰因子的取值可通過收斂性研究來確定。C 表示約束矩陣,其結構具體形式是通過約束有限元節(jié)點位移在整體有限元節(jié)點位移中的位置來確定的,是一個對角矩陣。當有限元節(jié)點位移被約束時,C 矩陣中對應的對角線元素取值為1,否則為0。根據(jù)上述得到的剛度矩陣和質量矩陣,波紋曲梁結構自由振動分析的運動方程可以寫成如下形式。

式中ω 和φ 分別表示系統(tǒng)特征頻率和特征向量,該式可以用于開展波紋曲梁結構自由振動特性研究。

2 算例分析

2.1 懲罰因子取值分析

由上所述,本文采用罰函數(shù)對波紋曲梁結構施加邊界條件。為了確定懲罰因子的取值,本節(jié)研究波紋曲梁結構固有頻率隨懲罰因子的變化規(guī)律,具體如圖2 所示。

圖2 波紋曲梁結構固有頻率隨懲罰因子的變化規(guī)律

從圖2 可以看出,波紋曲梁結構前三階固有頻率隨著懲罰因子的增加呈現(xiàn)先增加后保持不變的變化趨勢。為了保證模型的求解精度,懲罰因子取值為S=1011。為了便于后續(xù)模型求解,給出波紋曲梁結構邊界條件的定義：

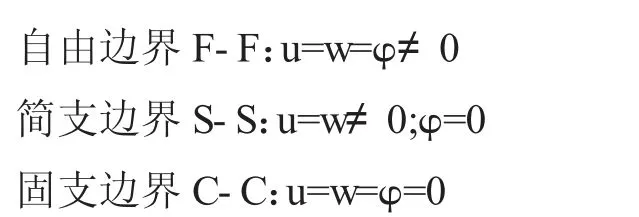
2.2 模型有效性驗證

由上所述,本文已經(jīng)建立了波紋曲梁結構自由振動特性分析模型。為了便于后續(xù)開展自由振動特性分析,本節(jié)對已建立波紋曲梁結構自由振動特性分析模型有效性開展模型驗證。模型有效性驗證主要包含兩部分,分別是曲梁結構自由振動特性分析模型有效性驗證和波紋曲梁結構自由振動特性分析模型有效性驗證。模型有效性驗證的具體措施是將本文模型的求解結果有限元軟件求解結果進行對比驗證。

首先開展曲梁結構自由振動特性分析模型有效性驗證,將本文模型求解結果分別與有限元軟件ABAQUS和ANSYS 軟件計算結果進行對比,對比結果如表1 所示。同時指出,曲梁結構模型參數(shù)為：E=2.1e11Pa；v=0.3；b=h=0.001m；R=0.5m；α=60°。

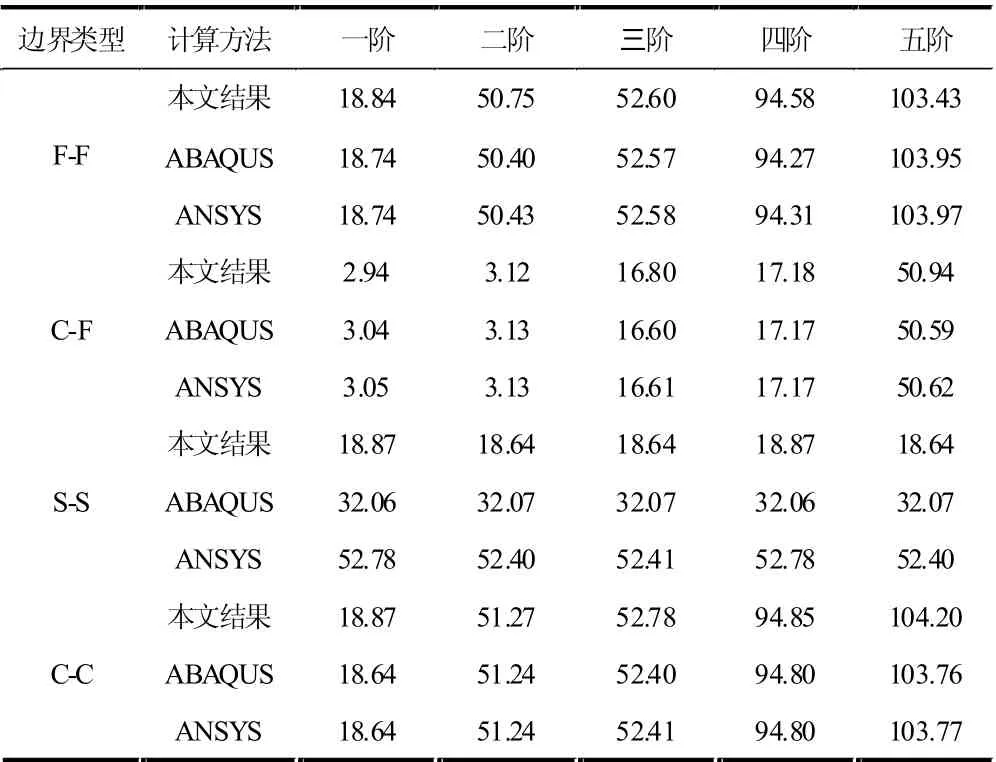
表1 曲梁結構模型的固有頻率對比驗證

從表1 不難看出,在不同邊界條件下,本文模型求解得到的前五階固有頻率與有限元軟件的計算結果具有較好的一致性。緊接著,開展波紋曲梁結構自由振動分析模型有效性驗證,對比結果如表2 所示。同時指出,波 紋 曲 梁 結 構 模 型 參 數(shù) 為：E=2.1e11Pa；v=0.3；2α1=α2=α3=α4=2α5=90°；b=h=0.01m；R=0.5m。

表2 波紋曲梁結構模型的固有頻率對比驗證

從表2 不難看出,在不同邊界條件下,本文模型求解的前五階固有頻率與有限元軟件求解結果在總體趨勢上具有較好的一致性,但是個別階數(shù)存在較大誤差。根據(jù)上述模型對比結果,本文模型能夠求解波紋曲梁結構在不同邊界條件下的自由振動特性。

2.3 模型參數(shù)化研究

由上所述,本文模型有效性已經(jīng)得到驗證,可以用于分析波紋曲梁結構在一般邊界條件下的自由振動特性。本節(jié)將通過研究波紋曲梁結構幾何參數(shù)對其在簡支邊界條件下自由振動特性的影響來開展波紋曲梁結構自由特性分析。

首先研究厚度對波紋曲梁結構固有頻率的影響,具體結果如圖3 所示。除了厚度h 以外,其余模型參數(shù)與表2 中所用的模型參數(shù)相同。

圖3 波紋曲梁結構固有頻率隨厚度的變化規(guī)律

從圖3 可以看出,在簡支邊界條件下,波紋曲梁結構前三階固有頻率隨厚度的增加而增加。結果表明,隨著厚度h 的增加,波紋曲梁結構固有頻率向高頻方向移動,波紋曲梁結構穩(wěn)定性得到顯著提高。

緊接著研究曲率半徑R 對波紋曲梁結構固有頻率的影響,具體結果如圖4 所示。除了曲率半徑R 以外,其余模型參數(shù)均與表2 中所用的模型參數(shù)相同。

圖4 波紋曲梁結構固有頻率隨曲率半徑的變化規(guī)律

從圖4 不難看出,在簡支邊界條件下,波紋曲梁結構前三階固有頻率隨曲率半徑R 的增加而減小。結果表明,隨著曲率半徑R 的增加,波紋曲梁結構固有頻率向低頻方向移動,波紋曲梁結構穩(wěn)定性顯著降低。

最后研究曲梁弧度α 對波紋曲梁結構前三階固有頻率的影響,具體結果如圖5 所示。除了曲梁弧度α 以外,其余模型參數(shù)與表2 中所用的模型參數(shù)相同。

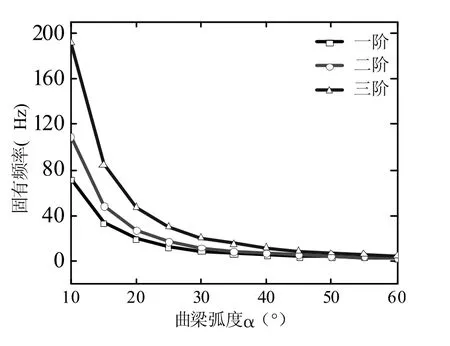
圖5 波紋曲梁結構固有頻率隨曲梁弧度的變化規(guī)律

從圖5 可以看出,前三階固有頻率隨著曲梁弧度的增加而減少。結果表明,隨著曲梁弧度α 的增加,波紋曲梁結構固有頻率向低頻方向移動,波紋曲梁結構穩(wěn)定性顯著降低。

3 結論

3.1 本文基于厚曲梁理論,采用有限元法建立一般邊界條件下波紋曲梁結構統(tǒng)一動力學分析模型。

3.2 將本文模型求解結果與有限元軟件計算結果進行對比,開展模型驗證。結果表明,本文模型求解具有較好穩(wěn)定性和求解精度,可以用于求解一般邊界條件下波紋曲梁結構的自由振動特性。

3.3 對已建立波紋曲梁結構開展參數(shù)化研究,結果表明隨著厚度增加,波紋曲梁結構共振頻率向高頻方向移動,穩(wěn)定性得到顯著提高。隨著曲率半徑和曲梁弧度的增加,波紋結構固有頻率向低頻移動,穩(wěn)定性得到顯著降低。