基于模擬退火的粒子群算法的船舶空調系統能耗優化研究

曾 建，楊祥國，劉自然，榮晨光

(武漢理工大學 能源與動力工程學院，湖北 武漢 430063)

船舶在不同海域航行時，為了保證船員工作生活環境的舒適性，都會設有空調系統，以維持艙室內空氣溫濕度的穩定[1]，但同時也為船舶帶來了較大的能耗問題，因此對于中央空調系統開展性能優化研究對船舶實現節能減排具有非常重要的意義。文獻[2]通過對不同分區的空調設備啟停控制來達到節能的效果，但未對系統的運行參數進行優化；文獻[3]以系統總能耗為優化目標，得到不同負荷下的最佳工況點，但是僅考慮了部件的物理約束；文獻[4]僅對水系統各個部件的節能特性進行了研究，沒有考慮風系統對空調系統能耗的影響。針對中央空調系統強耦合性的特點，要實現中央空調系統總能耗最低的目標，必須統一考慮系統與各部件之間的關聯與耦合。因此本文提出一種基于模擬退火的粒子群優化算法，對系統的運行參數進行優化，保證系統的最佳運行。

1 基于模擬退火的粒子群優化算法

1.1 粒子群算法

粒子群算法是一種基于群體的智能優化算法。在粒子群算法中，每個粒子(Particle)看作優化問題的解，在迭代過程中根據適應度(Fitness Value)來更新個體最優位置點pXibest與種群最優位置點gXbest，然后粒子更新自己的速度與位置，進行下一次迭代尋優。

粒子的速度和位置信息根據公式(1)、(2)來更新：

pvi,j(t+1)=ωvi,j(t)+c1r1[pxi,jbest-pxi,j(t)]+c2r2[gxi,jbest-pxi,j(t)]，

(1)

pxi,j(t+1)=pxi,j(t)+pvi,j(t) ,

(2)

式中，t為迭代次數，r1、r2為均勻分布在[0，1]之間的隨機數，c1、c2為算法學習因子，ω為慣性權重參數，pxi,j、pvi,j分別為粒子當前的位置與速度，pxi,jbest、gxi,jbest分別為粒子與種群當前的最優位置 。

本文采用一種非線性調整慣性權重的粒子群算法(ULωPSO)，該算法利用指數函數y=ex，其中x∈[-∞,0]，來非線性地調整慣性權重的下降。慣性權重參數ω的計算如公式(3)所示：

(3)

式中，tmax為最大迭代次數，ωmax和ωmin分別為慣性權重參數的最大值與最小值。

粒子群算法主要依靠群體間的競爭與合作，所以在運行的初始階段，算法的收斂速度較快，但粒子群算法存在易陷入局部最優、精度較低等缺點。

1.2 模擬退火算法

模擬退火算法是根據固體退火的熱力學原理，并廣泛應用于解決組合優化問題的算法。算法在優化過程中，首先確定初始溫度，隨機選擇一個初始狀態并進行評估；對當前狀態添加一個小擾動，重新評估該狀態的目標函數值，以1的概率接收較好的值，以概率k接受一個較差的值并更新狀態，通過迭代直到算法冷卻。

模擬退火算法具有漸進收斂性，只要初始溫度T0足夠高，退火流程足夠慢，該算法理論上會以100%的概率收斂到全局最優解。但是搜索空間較大時，需要花費較長的迭代時間才能夠收斂得到一個高質量的近似最優解，收斂速度慢，不滿足大規模實際問題的應用需求。

1.3 基于模擬退火的粒子群優化算法

針對粒子群算法與模擬退火算法各自的特點，本文提出了一種基于模擬退火的粒子群算法(SA-ULωPSO)，其將Metropolis準則中的粒子取舍機制引入到非線性慣性權重粒子群算法(ULωPSO)中，不僅保持了粒子群算法收斂速度快的優點，同時還改善了算法早熟收斂問題，增加了搜索的多樣性。

基于模擬退火的粒子群算法的尋優步驟如下。

1)設定粒子的個數N，初始化粒子的位置pXi和速度pVi、設定最大迭代次數tmax、慣性權重參數ω、初始溫度T0、降溫系數φ以及允許變壞的范圍β。

2)初始化個體最優位置pXibest、種群最優位置gXbest、個體最優值pFibest以及種群最優值gFbest。

3)計算微粒的適應度，通過比較更新pXibest、gXbest、pFibest以及gFbest。

4)根據公式(1)～(2)，更新粒子的速度與位置。

5)計算粒子位置更新后的適應度變化量Δf=f(pNxi,j)-f(pxi,j)，pNxi,j為更新后的粒子位置，如果Δf<β，則更新種群最優位置;否則，計算k=exp(-Δf/T)，T為退火溫度，若k大于在[0,1]中選取的任何一個隨機數，則更新種群最優位置；否則，保持原先的位置與速度不變。

6)如果迭代達到最大次數tmax或者達到預期精度，算法收斂，當前gXbest和gFbest就是最終結果；否則更新慣性權重參數ω、退火溫度T以及迭代次數t，返回步驟3)，算法繼續，直到滿足終止條件。

2 中央空調系統優化模型的建立

本文以某海洋平臺工作區中央空調系統為研究對象，空調面積844 m2，冷水機組2臺(一用一備)，額定制冷量為210 kW 。中央空調系統結構示意圖如圖1所示。

2.1 優化目標函數的建立

中央空調系統的主要能耗設備包括冷水機組、冷凍水泵、冷卻水泵、空調機組風機，即：

Ptotal=Pchiller+Pchwp+Pcwp+Pcfan，

(4)

式中，Ptotal為中央空調系統總能耗，Pchiller為冷水機組能耗，Pchwp為冷凍水泵能耗，Pcwp為冷卻水泵能耗，Pcfan為空調機組能耗。

各設備的能耗表示如下：

(5)

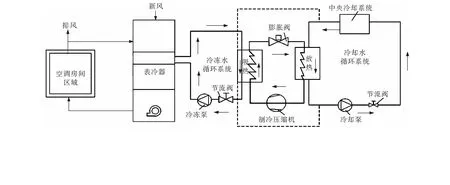
圖1 中央空調系統結構示意圖

(6)

(7)

(8)

式中，Tchwo為冷凍水供水溫度，Tcwi為冷卻水供水溫度，qmchw、qmcw分別為冷凍水和冷卻水流量，qvf為風機流量 。

綜合考慮各設備運行特性和設備間耦合關系，確定中央空調系統的優化變量，包括冷凍水供水溫度、冷凍水流量、冷卻水流量、空調機組風量、空氣濕球溫度和冷負荷。

2.2 約束條件的確定

中央空調系統具有強耦合性，因此優化模型的約束條件不僅包括設備本身的物理約束，還包括設備之間的相互約束。

1)冷水機組的進出水溫約束。

Tchwo,min≤Tchwo≤Tchwo,max。

(9)

2)冷凍水與冷卻水流量的約束。

qmchw,min≤qmchw≤qmchw,max，

(10)

qmcw,min≤qmcw≤qmcw,max。

(11)

3)空調機組風機流量的約束。

qvf,min≤qvf≤qvf,max。

(12)

4)空調機組與冷凍水泵之間的約束。

(13)

式中，Qa為空調機組實際供冷量，Qa,0為空調機組額定供冷量，Twb為實際空氣濕球溫度，Twb,0為額定空氣濕球溫度，Tchwo,0為冷凍水額定供水溫度，qmchw,0為冷凍水額定流量，qvf,0為空調機組額定風機流量。

5)冷水機組與冷凍水泵，冷卻水泵相互之間的約束。

Qchiller=qmchwcw(Tchwo-Tcwi)，

(14)

Pchiller+Qchiller=qmcwcw(Tcwi-Tchwo)，

(15)

式中，Qchiller為冷水機組供冷量，cw為水的比熱容。

由此得到中央空調系統優化的約束條件如下：

(16)

3 仿真與分析

基于前文建立的中央空調系統能耗優化模型，運用基于模擬退火的粒子群算法和非線性慣性權重粒子群算法分別對系統進行參數優化，比較分析不同工況下2種算法的節能效果。

3.1 不同負荷情況下的優化分析

設定冷負荷為額定負荷的70%，空氣濕球溫度為25 ℃，分別運用2種算法對中央空調系統參數進行優化，并對比結果。SA-ULωPSO算法的設定參數如表1所示,ULωPSO算法除缺少β、T0、φ這3個參數外，其余參數與SA-ULωPSO算法參數一致。

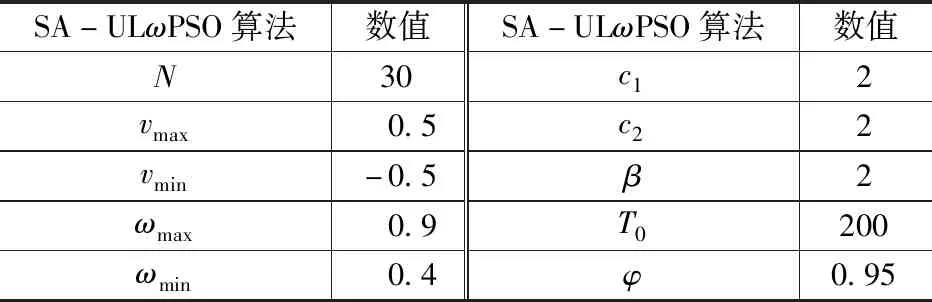
表1 SA-ULωPSO算法的設定參數

設定最大迭代次數為200次，得到負荷率70%時，2種算法對空調系統參數的優化對比如圖2所示。由圖2可知，利用SA-ULωPSO算法進行優化時，當迭代次數達到39時算法收斂，此時的能耗為52.15 kW;利用ULωPSO算法進行優化時，當迭代次數達到61時算法收斂，此時的能耗為54.04 kW，因此可知SA-ULωPSO算法的收斂速度和收斂精度都優于ULωPSO算法。

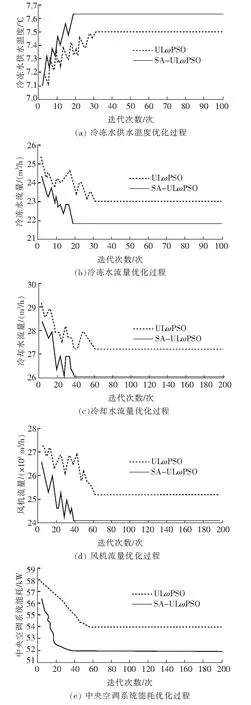
圖2 負荷率70%時，2種算法對空調系統參數的優化對比

設定負荷為90%時，2種算法對空調系統參數的優化對比如圖3所示。由圖3可知，利用SA-ULωPSO算法進行優化時，當迭代次數達到42次時，算法收斂，此時的能耗為66.44 kW;利用ULωPSO算法進行優化時，當迭代次數達到63次時，算法收斂，此時的能耗為70.23 kW。

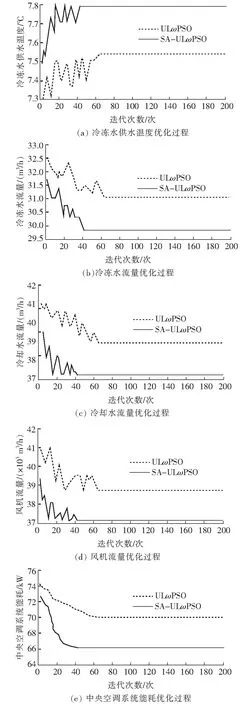
圖3 負荷率90%時，2種算法對空調系統參數優化對比

3.2 一個制冷周期的優化分析

本文選取7月份某日的空調系統運行數據，對提出的算法進行仿真驗證，當日冷負荷與空氣濕球溫度變化曲線如圖4、圖5所示，并將其作為優化模型的輸入。

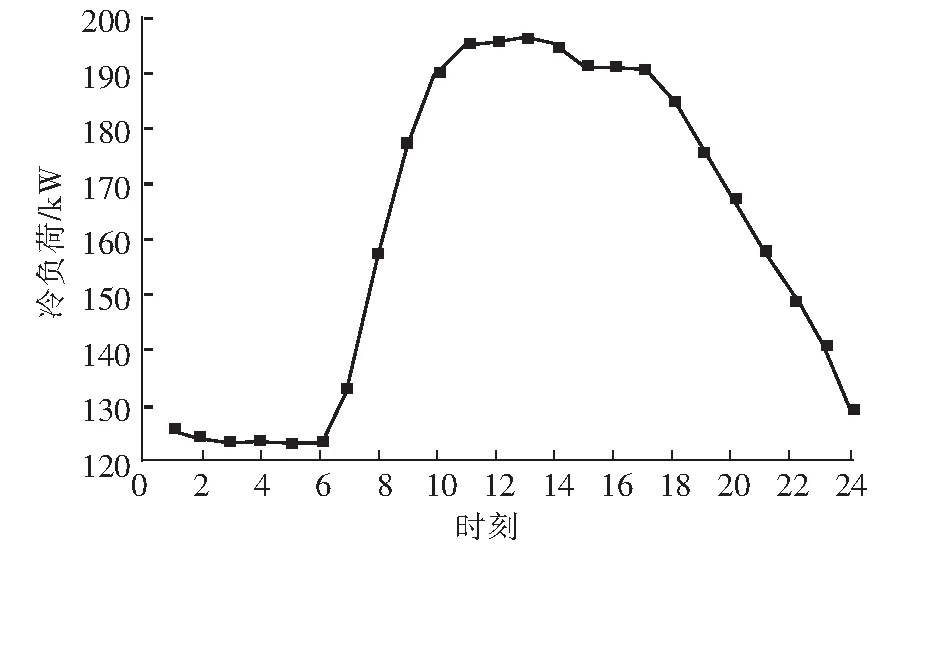
圖4 冷負荷變化曲線

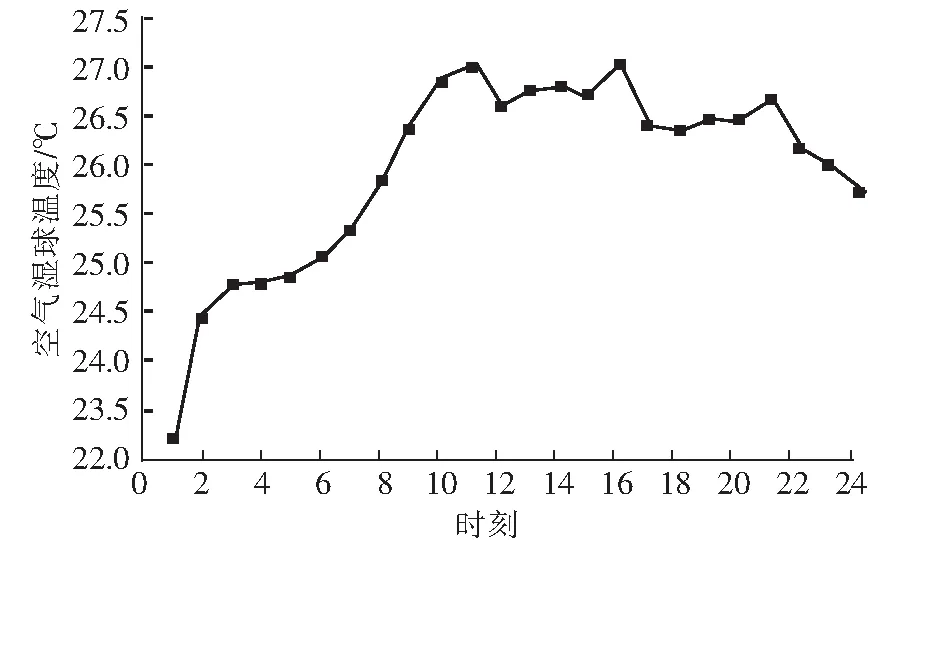
圖5 空氣濕球溫度變化曲線

在一個制冷周期內，房間的冷負荷是不斷變化的，因此空調系統的工況點也會隨之不斷變化，分別采用2種算法對空調參數進行優化，得到優化后的中央空調系統總能耗對比如圖6所示。由圖6可知，8時之前與19時之后，系統冷負荷較小，因此空調優化前后總能耗相差較大，而在8時到19時之間，由于室外溫度與濕度的提高，使得系統的負荷增大，優化前后能耗差別不大，說明算法優化的系統節能率隨著負荷的變大而減小。表2為空調系統各設備的能耗對比，其中冷水機組和空調機組的節能率較大，這是因為冷凍水供水溫度提升后，使得冷水機組的蒸發效率提高，因而提高了機組的能耗比，最終系統總節能率為9.07%，優化節能效果良好。

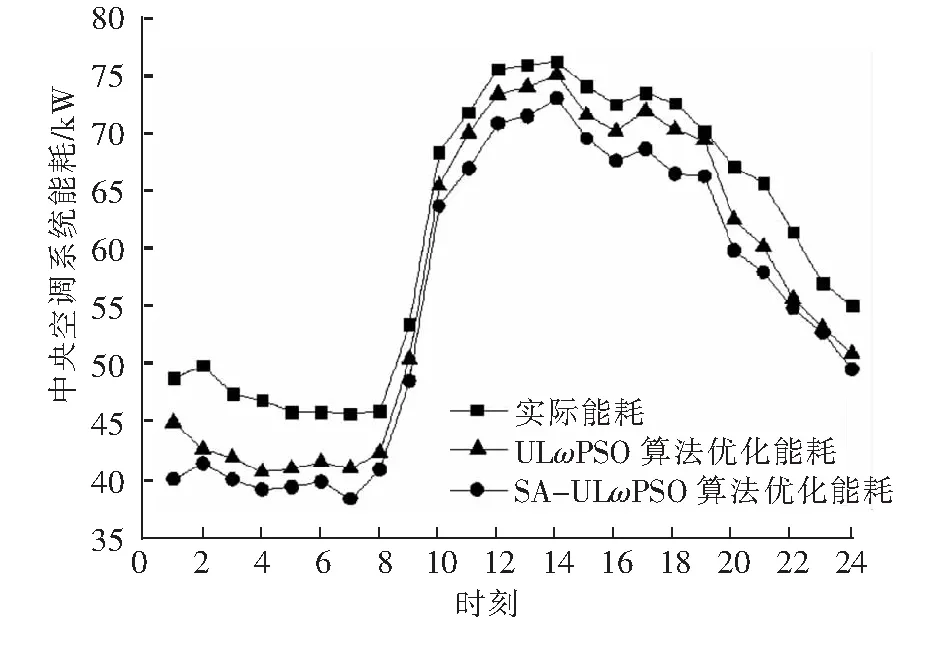
圖6 優化后的中央空調系統總能耗對比

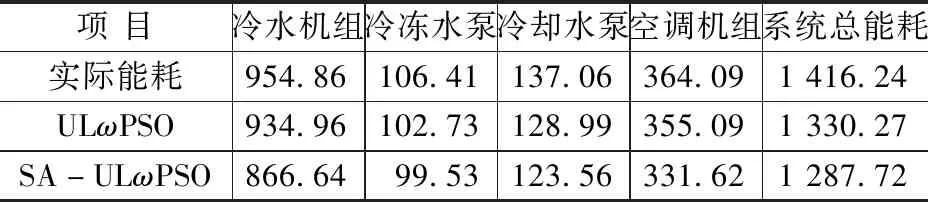
表2 空調系統各設備能耗對比 kW

4 結束語

本文提出一種基于模擬退火的粒子群算法，以中央空調系統總能耗為目標函數，建立中央空調系統的優化模型，分別運用基于模擬退火的粒子群算法和非線性慣性權重粒子群算法對中央空調系統優化模型進行參數優化，通過對不同工況下2種算法的收斂速度與能耗比較，表明本文設計的基于模擬退火算法的粒子群算法在收斂速度和節能效果上都有明顯優勢。