智能壓電材料MFC在太陽電池陣帆板上的主動抑振研究

駱海濤，吳星元，劉廣明，富 佳

（1.中國科學院沈陽自動化研究所機器人學國家重點實驗室，遼寧沈陽 110016；2.中國科學院機器人與智能制造創(chuàng)新研究院，遼寧沈陽 110169；3.沈陽理工大學機械工程學院，遼寧沈陽 110159）

引言

在空間環(huán)境中，太陽電池陣在軌展開、對日定向調整和受到航天器機動變軌所產生的干擾，均會使得電池陣的帆板產生振動。太陽電池陣為薄壁結構，由于自身幾何尺寸大和材料非線性大變形的特性使得電池陣柔度增大，而太空環(huán)境為低阻尼的狀態(tài)，振動難以得到快速衰減，長時間的持續(xù)振動會造成敏感器件的破壞，航天器需要更長的時間和消耗更多的燃料來進行姿態(tài)調整，還會影響到航天器或衛(wèi)星本體的指向精度和姿態(tài)穩(wěn)定，對其姿態(tài)控制和工作造成極其不利的影響。因此，為了保證航天器或衛(wèi)星的指向精度和姿態(tài)穩(wěn)定，對太陽電池陣振動的快速抑制勢在必行。

國內外關于電池陣主動抑振問題已有一定的研究，其中華南理工大學邱志成老師團隊對電池陣系統(tǒng)建立了特征模型，并通過線性二次型（Linear Quadratic Regulator，LQR）控制［1］和正位置反饋控制（Positive Position Feedback，PPF）控制［2-4］驗證了主動控制的可行性。Omidi等［5］提出了改進的正位置反饋控制（Modified Positive Position Feedback，MPPF）。Williams 等［6］基于MFC 設計了主動控制系統(tǒng)，用于懸臂梁的主動抑振。Sharma 等［7］詳細研究了壓電材料在不同工作模式下的驅動電壓，以及相應的極化方向。Vishal等［8］提出了一種用形狀記憶合金絲作驅動器的懸臂梁振動主動抑制方法，將壓電纖維增強復合材料應用于懸臂梁的主動抑振中［9］。關于懸臂梁主動控制中的致動器分布位置的研究，Guzmán 等［10］提出了一種拓撲優(yōu)化的致動器分布方法。Wang 等［11］使用光學相機監(jiān)測懸臂梁振動，通過Lyapunov 方法進行系統(tǒng)閉環(huán)穩(wěn)定及主動控制時的模型預測［12-14］。在主動抑振系統(tǒng)中，多是基于小型懸臂梁的系統(tǒng)驗證，大型太陽電池陣的控制系統(tǒng)應用很少，實際太陽電池陣由于結構復雜，面臨太空中的各種擾動，振動情況尤為復雜。懸臂梁單端固定的分析方法與實際帆板的鉸鏈安裝方法也有很大的區(qū)別，一些對于數(shù)學模型依賴較高的算法即使在懸臂梁試驗效果良好，應用到工況復雜的帆板上仍然面臨嚴峻的挑戰(zhàn)。

本文針對太陽電池陣系統(tǒng)振動控制問題，設計了一套基于MFC 的振動主動控制系統(tǒng)。分析了MFC 作為傳感器和致動器的正逆壓電效應機理；基于系統(tǒng)辨識的方法，在實驗的基礎上建立了電池陣振動的數(shù)學模型，通過應變能最大理論確定了MFC最佳粘貼區(qū)域；采用PID 自整定的控制算法，確立了分立式MFC 驅動器的振動控制參數(shù)，實現(xiàn)了可以獨立控制MFC 抑振的目標。

1 抑振機理分析及數(shù)學模型建立

1.1 壓電纖維復合材料抑振機理分析

壓電陶瓷在懸臂梁的振動抑制中有著廣泛的應用，但是壓電陶瓷本身剛性較大，形變較小，所以NASA 基于壓電陶瓷設計了一種新型復合材料即MFC，由于本質是壓電陶瓷，所以同樣具有正逆壓電效應，MFC 具有一定的柔度，同面積的MFC 產生的應變力大于壓電陶瓷的十倍。本文基于正逆壓電效應，將MFC 作為致動器和傳感器，MFC 內部結構較為復雜，是由很多細條的壓電陶瓷通過交叉電極相連，這樣即使其中的部分壓電陶瓷發(fā)生斷裂，MFC 還是能完成一定的作為致動器或者傳感器的工作。MFC 材料的工作原理解析如圖1所示。

圖1 MFC 工作原理Fig.1 MFC working principle

當MFC 作為致動器時，根據(jù)逆壓電效應，致動器的輸出可以用電位移D和電場強度E來描述［15］：

式中 電位移D的單位為C/m2，電場強度E的單位為V/m，Ei和Di（i=1，2，3）的下標表示分量沿參考系的軸向。εii為介電常數(shù)，表示介質極化程度，單位為F/m，對于極化后的壓電陶瓷材料，只有ε11=ε22≠0 和ε33≠0，則：

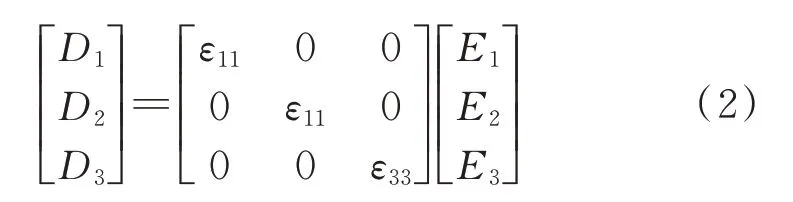
在上述情況下，壓電陶瓷的輸出也可以用應變S和電場強度E來描述：

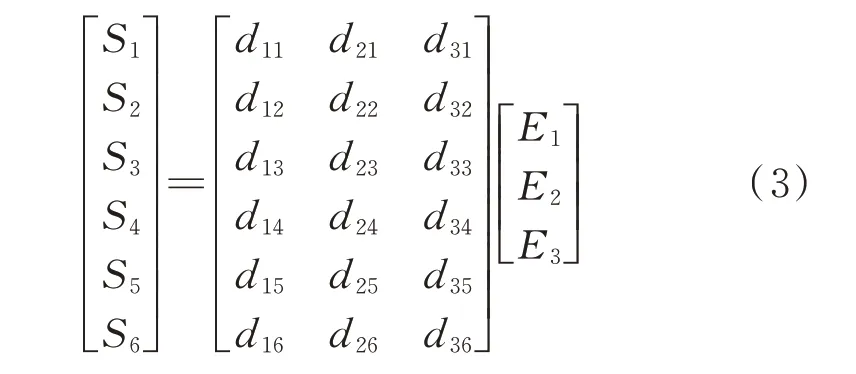
式中d為壓電應變常數(shù)，表示壓電元件將機械能轉換為電能或者電能轉化為機械能的比例常數(shù)。對于極化后的壓電陶瓷，由于對稱性，其壓電應變常數(shù)矩陣為：

由于d31=d32，d15=d24，因此只有d31，d33和d15三個獨立分量。

壓電材料的結構應變與應力T之間的關系，根據(jù)虎克定律有：

式中Sij為彈性柔順系數(shù)，它是描述介質彈性物理量，單位為m2/N。

根據(jù)式（3）和（4）構建聯(lián)合公式，其分量的形式為：

同理，電位移D則由其承受應力和電場強度產生，其張量分量形式為：

式中diuTu為應力引起的的電位移：為當應力為0 的情況下，由外電場作用產生的電位移，表示應力T=0 或者為常數(shù)時的介電常數(shù)。

式（5）和（6）是分別以電場強度Ej和應力Tu為自變量的壓電方程，也被稱為第一類壓電方程。當然也有以其他變量構造的其他類的壓電方程，本文中以第一類壓電方程進行描述。

對于Smart Material 公司生產的MFC，根據(jù)電極極化方向的不同，主要制作成以d33和d31效應工作的MFC。本文中選用的兩種P1 型MFC 是以d33效應工作的。基于d33效應，當兩極施加電壓后，壓電復合纖維會伸長或者縮短。當MFC 作為致動器時，通過施加在電極上的電壓可知此時E3≠0，E1=E2=0，因此將式（5）展開有：

通過上式可知，S4，S5，S6均不反映施加電場后的影響，因此進一步簡化該式有：

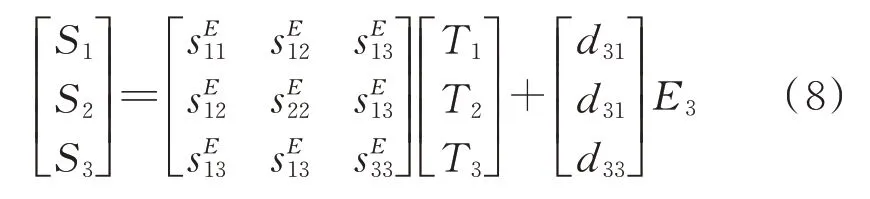
類似于式（5）展開，將式（6）展開有：

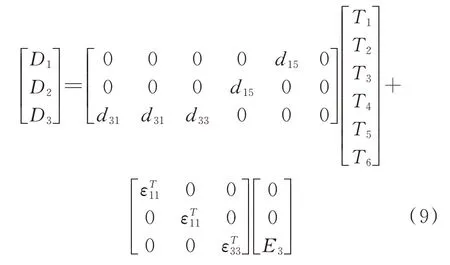
觀察上式可知，電位移D1和D2均不反映施加電場后的影響，因此進一步化簡該式有：

綜合式（8）和（10），可以得到MFC 的第一類壓電方程：

關于MFC 粘貼位置的研究中，多是基于通過有限元建立懸臂板的數(shù)學模型，以此作為理論依據(jù)來確定MFC 粘貼位置［16］，在本文中，通過MSC.Nastran 軟件分析，立足于最大應變能理論確定MFC 最佳粘貼位置。對于帆板模型的結構和材料參數(shù)如表1所示。

表1 抑振系統(tǒng)材料參數(shù)Tab.1 Material parameters of vibration suppression system

帆板模型的尺寸來源是“向日葵”衛(wèi)星太陽翼單板的實際尺寸，利用軟件分析帆板模型的振動模態(tài)，如圖2所示，是帆板第1 階的應變分析圖形。通過軟件設置采用應變顯示選項，從圖中可以看到最大應變位置位于末端固定位置以及鉸鏈連接的位置。

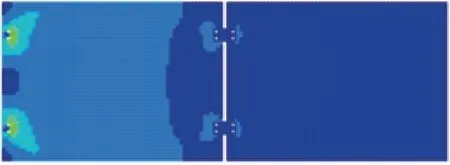
圖2 帆板結構第1 階應變分析Fig.2 The first order strain analysis of sailboard structure

由于應變分布主要集中在帆板結構固定位置，所以第1 階振型反映了主要的應變集中位置，這些位置也是指導粘貼MFC 的主要依據(jù)。表2所示是通過模態(tài)分析的帆板前8 階的振型，主要反映的是各階的具體振動頻率，剛度。

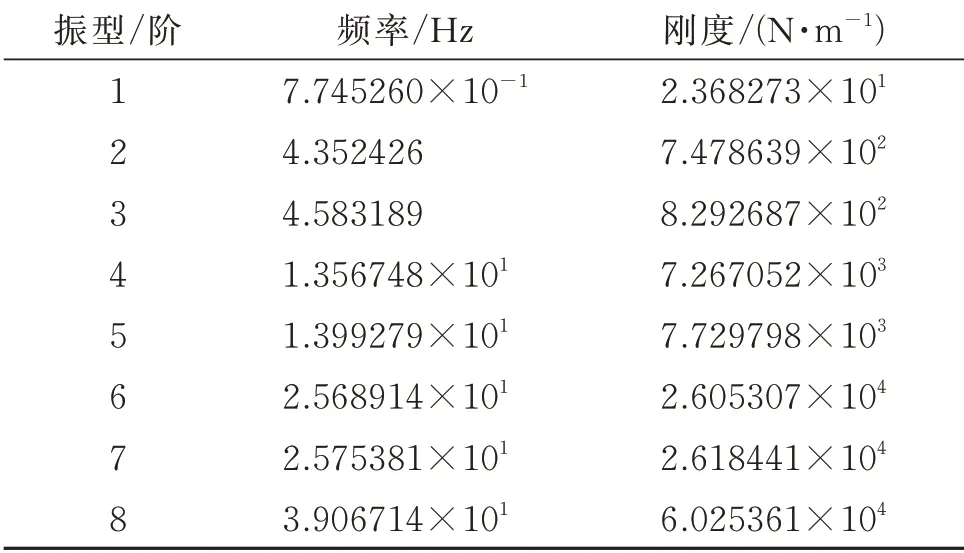
表2 帆板模型模態(tài)分析振型表Tab.2 Modal analysis table of sailboard model

1.2 帆板振動數(shù)學模型建立

在不考慮板結構非線性的情況下，可以將帆板的振動情況近似為一個2 階系統(tǒng)［17］。典型的2 階系統(tǒng)傳遞函數(shù)為：

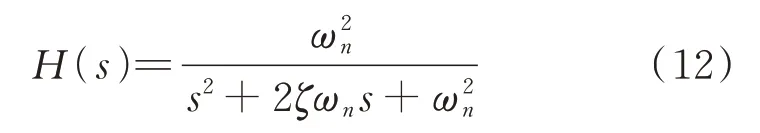
式中ζ為阻尼比；ωn為自由振動頻率。

采用系統(tǒng)辨識的思想，通過激光位移傳感器測得帆板自由振動的波形。如圖3所示是實驗帆板安裝的位置關系，單板之間通過鉸鏈進行連接。由于激光位移傳感器ZLDS103-250的起始量程為65 mm，量程為250 mm，并且帆板振動是基于平衡位置做往復運動，所以帆板和激光位移傳感器間距190 mm。

圖3 帆板安裝位置關系Fig.3 Installation position relationship of sailboard

通過激光位移傳感器測得帆板自由振動波形圖，如圖4所示。數(shù)據(jù)采集通過LabVIEW 作為上位機，由通過軟件模態(tài)分析得出的帆板的振型可知，帆板振動的頻率很低，所以設置1 KS/s的采樣率即采樣周期為Tc=0.001 s，足以滿足要求。圖中，橫坐標表示的是采樣點數(shù)，反映的是時間，縱坐標表示的是振動幅度。

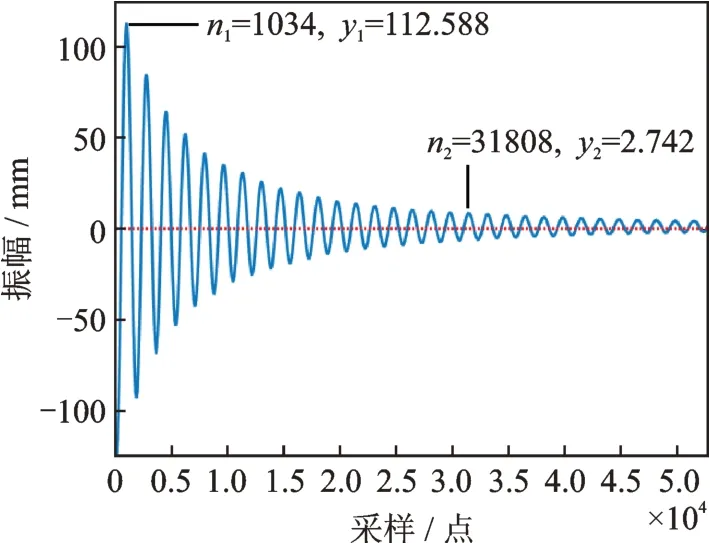
圖4 帆板實驗測量自由振動波形Fig.4 Measurement of free vibration waveforms in sailboard experiment

已知2 階系統(tǒng)工作在欠阻尼的情況時，其振動響應為：

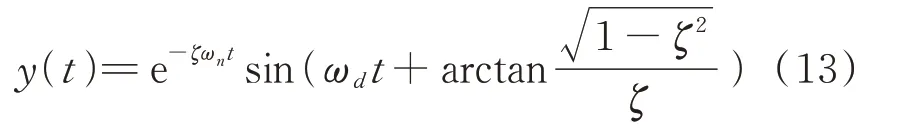
如圖4所示的周期為T的自由振動波形中，取t1，t2兩個時刻的峰值y1，y2，兩個時刻相差k個周期，對應的采樣點分別為n1，n2，由式（13）可得：

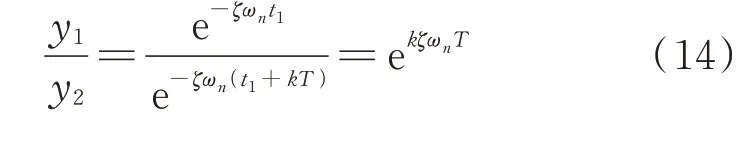
其中：

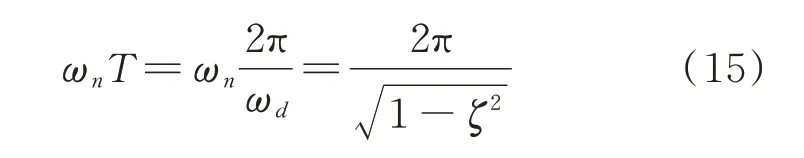
將式（15）代入式（14）中，得到：

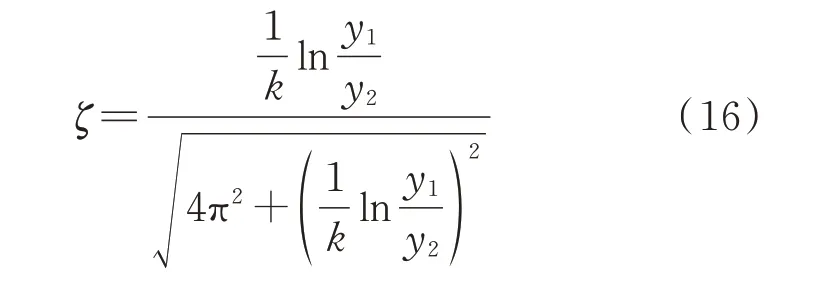
選中圖中兩個點(n1，y1)和(n2，y2)，n1=1034，y1=112.588，n2=31808，y2=2.742，k=18，代入式（16）中，解得阻尼比ζ=0.033。

根據(jù)采樣點以及采樣周期可以求出帆板的振動周期和頻率分別為：

由式（15）可得：

將阻尼比ζ，自由振動頻率ωn代入式（12）可得系統(tǒng)的傳遞函數(shù)為

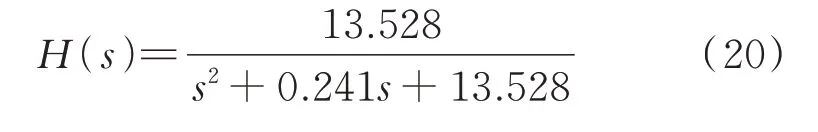
2 主動抑振實驗研究

2.1 實驗系統(tǒng)介紹

主動抑振系統(tǒng)包括上位機控制系統(tǒng)、信號采集系統(tǒng)、數(shù)據(jù)轉換系統(tǒng)、信號驅動系統(tǒng)、執(zhí)行機構五部分組成。

上位機控制系統(tǒng)是通過LabVIEW 開發(fā)的，上位機主要負責信號處理，由于上位機接收到的是USB-6002 的信號，其中的信息是激光位移傳感器輸出的0～10 V 的電壓信號，通過激光位移傳感器對MFC進行標定，這樣LabVIEW 處理的信號和Simulink 仿真的信號可以匹配，在Simulink 中計算得到PID 控制參數(shù)也就能運用到實際的控制系統(tǒng)中。為了保證初始振動的同一性，需要給出一個固定的初始激振信號。整個上位機控制系統(tǒng)面板如圖5所示。

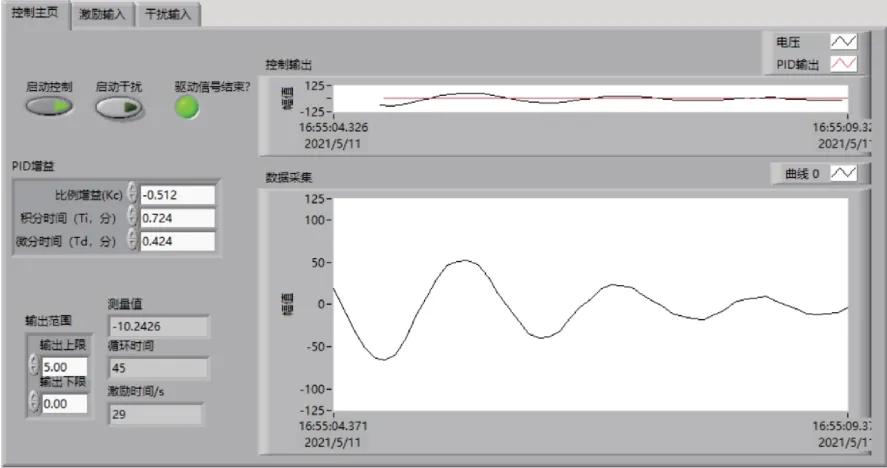
圖5 上位機控制面板Fig.5 Upper computer control panel

信號采集系統(tǒng)由MFC 作為傳感器和激光位移傳感器，主要目的是利用激光位移傳感器對MFC 做傳感器進行標定，因為在太空中，使用激光位移傳感器測位移是不現(xiàn)實的。當MFC 作為傳感器時，由于輸入電阻的原因，直接測量的電壓會失真，所以采用兩個1 MΩ 的電阻對MFC 采集的電壓分壓。USB-6002 測試的最高電壓為10 V，將分壓后的信號再輸入USB-6002 中，這樣就可以避免失真。

數(shù)據(jù)轉換系統(tǒng)采用的是NI 公司的數(shù)字板卡USB-6002，該板卡能采集8 路分辨率為16 位的模擬信號，最大采樣率可達50 KS/s，同時該板卡具有兩個16 位D/A 轉換輸出，適合本實驗中應用。

信號驅動系統(tǒng)采用的是適配MFC 的驅動器，是由Smart Material 公司生產的AMD2012-CE2/3驅動板，該驅動板最大輸出功率可達4 W，輸出電壓為-500～+1500 V。

執(zhí)行機構以MFC 作致動器，本課題使用的MFC 有M-5628-P1 和M-4312-P1 兩種類型，極限輸出力分別為340 和120 N。整個系統(tǒng)的控制流程圖如圖6所示。

圖6 實驗系統(tǒng)控制流程圖Fig.6 Control flow chart of experimental system

2.2 基于PID 自整定的主動控制算法

在PID 控制中，需要知道控制參數(shù)的值，由于PID 設置參數(shù)的值一般需要豐富的經驗，為了縮短調節(jié)參數(shù)的時間，將帆板振動的數(shù)學模型導入Simulink 中，通過軟件模擬的方式，快速得到一組或者幾組比較合理的控制參數(shù)，這里使用的是PID 自整定的方式，可以快速求得PID 控制參數(shù)。

在Simulink 中，繪制PID 自由振動模型及PID控制模塊，整體框圖如圖7所示。

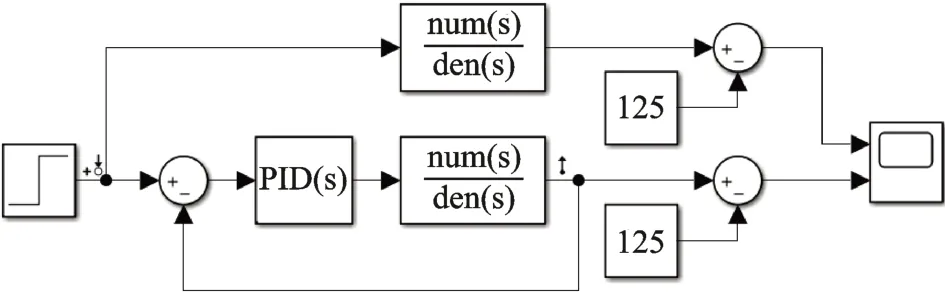
圖7 Simulink 參數(shù)整定系統(tǒng)框圖Fig.7 Block diagram of Simulink parameter setting system

如上圖所示，輸入信號為一個階躍信號，其值為：

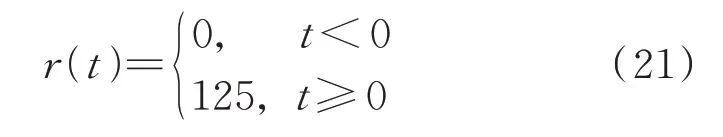
式中的終值125 是激光位移傳感器的測量極限范圍的1/2，在實驗中設為0 點的位置。為了方便觀察和理解在結果輸入示波器模塊前再減125，這樣就可以在Simulink 的示波器中觀察到測量數(shù)據(jù)是在以y=0 為基準變化的。

PID 控制的主要依據(jù)是通過輸入信號r(t)與輸出信號y(t)構成控制偏差e(t)，即：

PID 控制器是一種線性控制器，通過線性組合偏差的比例、積分、微分，將三者作為控制量進而控制受控對象。其控制規(guī)律為：

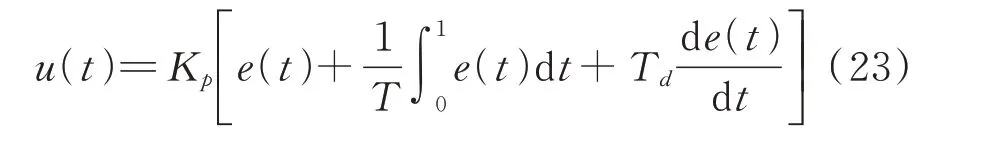
其傳遞函數(shù)為：

式中Kp為比例系數(shù)，Ti為積分時間常數(shù)，Td為微分時間常數(shù)。

在Simulink 的PID 模塊中，傳遞函數(shù)為：

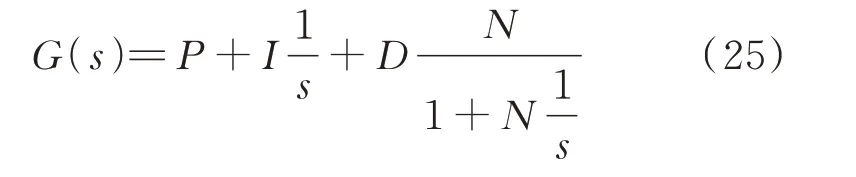
式中P為控制的比例參數(shù)，I為積分參數(shù)，D為微分參數(shù)，N為濾波系數(shù)。對比式（24）和（25）可以看到Simulink 的PID 參數(shù)和傳遞函數(shù)的系數(shù)的差異，所需要的是PID 的參數(shù)。

在被控對象模塊中輸入式（20）的各項系數(shù)，輸入形式為數(shù)組，如圖8所示。

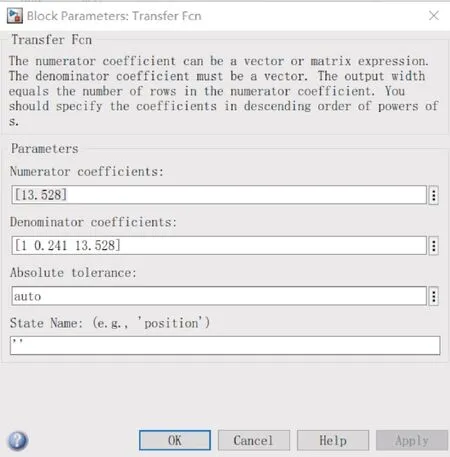
圖8 被控對象傳遞函數(shù)輸入Fig.8 Transfer function input of controlled object

為了形成控制輸入的對比，需要引入兩組相同的傳遞函數(shù)，其中一組不引入PID 控制直接輸出。

在完成輸入模塊，PID 模塊以及被控對象模塊等模塊的參數(shù)設置之后，便可利用Simulink 進行參數(shù)自整定從而得到一組比較合適的PID 控制參數(shù)。在Matlab 2020a 中能夠比較方便地利用Simulink 的工具包得到想要的的參數(shù)。通過Simulink 自整定之后的參數(shù)如圖9所示。

圖9 PID 自整定參數(shù)Fig.9 PID self tuning parameters

2.3 太陽能電池陣抑振效果評價

為了保證系統(tǒng)振動的初始激振信號一致，通過前面的實驗波形可知，帆板的自由振動波形的頻率為0.586 Hz。所以，在上位機中設置激振頻率與自由振動的頻率相同，激振信號幅值為5 V，頻率為0.586 Hz 的正弦信號，如圖10所示。

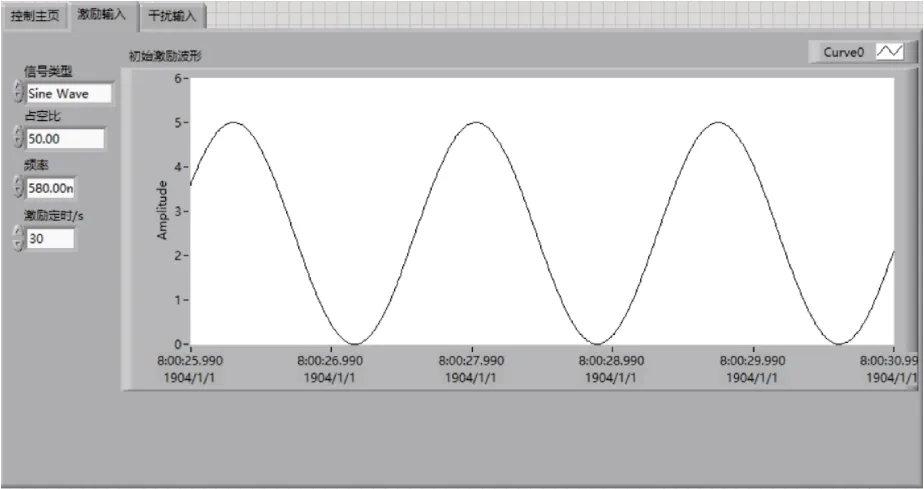
圖10 初始激振信號Fig.10 Initial excitation signal

通過上位機，可以采集到的三組振動信號，其中有兩組由MFC 作為傳感器采集，另一組由激光位移傳感器采集，激光位移傳感器采集的信號主要用于做參數(shù)標定并且保證與MFC 的數(shù)據(jù)匹配。

由于激光位移傳感器的位置定于中軸線上，所以只能采集彎曲振動的信號，而扭轉振動的信號可通過傳感器MFC 采集。

通過采集的激光位移傳感器的信號作為反饋，在LabVIEW 上編寫PID 控制程序，由于前期仿真使用實際模型仿真，在Simulink 中通過自整定PID得到的PID 參數(shù)為kc=-0.512，ki=0.724，kp=0.424。由于實際模型和在Simulink 中的仿真模型通過前期的參數(shù)標定，所以直接將仿真得到的控制參數(shù)代入LabVIEW 控制程序中，實驗結果如圖11所示。

圖11 自由振動有無控制實驗對比Fig.11 Experimental comparison of free vibration with and without control

為了驗證帆板在有干擾的環(huán)境下主動抑振效果，分別加入正弦波干擾、白噪聲干擾。其中，正弦信號的幅值為5 V，頻率為0.586 Hz。圖12所示為引入正弦波干擾的情況下，有無控制的波形對比；圖13所示為引入白噪聲干擾的情況下有無控制的波形對比。

圖12 正弦波干擾有無控制對比Fig.12 Comparison of sine wave interference with and without control

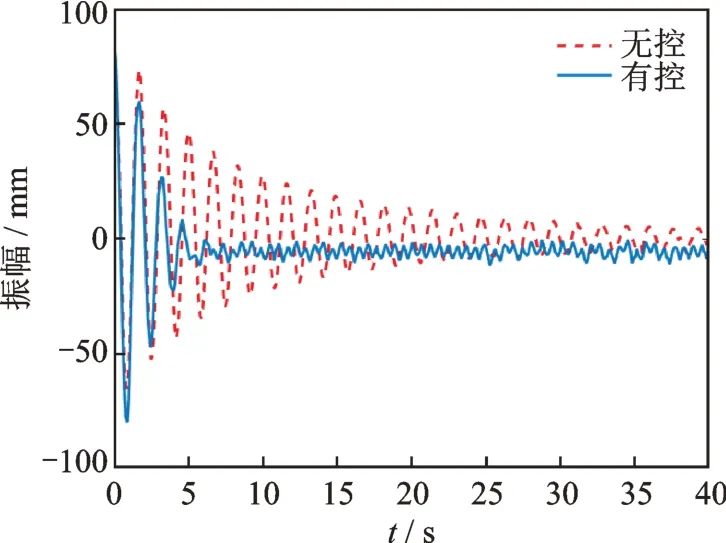
圖13 白噪聲干擾有無控制對比Fig.13 Comparison of white noise interference with and without control

通過實驗數(shù)據(jù)可以看到，自由振動在無主動抑振時呈負指數(shù)衰減，與數(shù)學模型對應，在引入PID 控制的三個振動周期后，振動得到了有效抑制，并且維持在一個比較穩(wěn)定的范圍內。

通過圖12 和13 可以看出：當引入干擾后，帆板的振動狀態(tài)發(fā)生了改變。而這兩種干擾狀態(tài)下PID的控制參數(shù)都是相同的，但是從圖中可以看出，相同的PID 控制參數(shù)對于兩種不同的干擾，仍然具有良好的抑振效果。

如圖14所示，為自由振動情況下對有無主動控制的波形的快速傅里葉變換（以下簡稱FFT（Fast Fourier Transform），從圖中可以看到，對于在共振頻率下的振動抑制較為明顯，這說明在基于MFC 的主動抑振過程中，MFC 的抑振是給帆板一個相同頻率的反作用力來達到抑制振動的目的，帆板的固有頻率是需要實驗和仿真測得的，也是前期建立數(shù)學模型和實驗的必要參數(shù)。

圖14 自由振動情況下的FFTFig.14 FFT in free vibration

類似地，在引入干擾的情況下，圖15所示為正弦波干擾輸入時，有無主動控制的FFT 變換波形對比；圖16所示為白噪聲干擾輸入時，有無主動控制的FFT 波形對比，從圖中可以觀察到，不同干擾輸入的情況下，主動控制的效果是類似的，都能對基頻附近的振幅有較明顯的抑制作用。

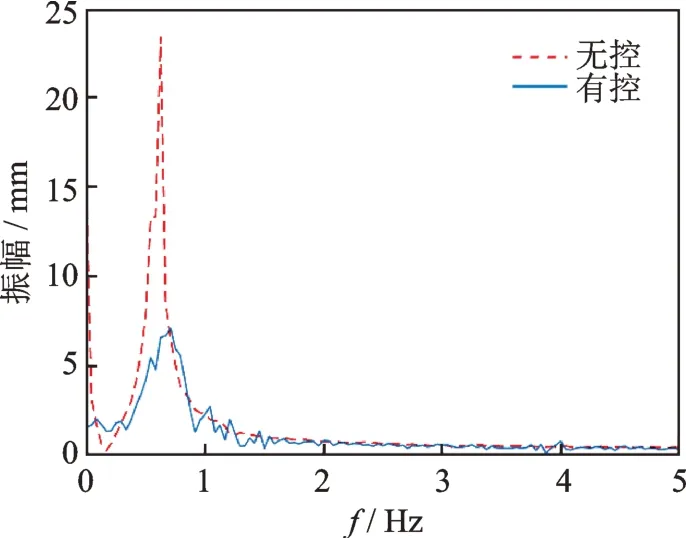
圖15 正弦波干擾輸入情況下的FFTFig.15 FFT in the case of sinusoidal interference input

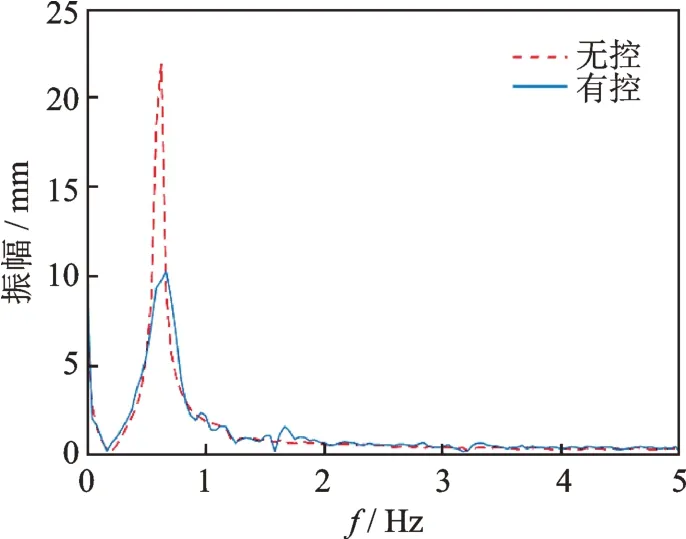
圖16 白噪聲干擾輸入情況下的FFTFig.16 FFT in the case of white noise interference input

實驗中提供的干擾信號是自然界中普遍存在的，在現(xiàn)有實驗條件下，干擾激勵的MFC 為M-4312-P1 型，此MFC 提供的最大輸出力為120 N，要比M-5628-P1 型MFC 的最大輸出力340 N 要小，這也就是在引入干擾后振動幅值有所下降的原因。

3 結論

本文設計了一套基于壓電纖維復合材料MFC 的太陽電池陣帆板主動抑振系統(tǒng)，該系統(tǒng)基于MFC的逆壓電效應在MFC上加載電壓，使其產生驅動力用于抑制帆板的振動。開展了基于MFC的抑振機理分析，推導了電池陣帆板的振動模型。在此基礎上，采用高性能的PID 控制算法，實現(xiàn)了電池陣帆板的主動抑振。通過對比自由振動以及正弦和白噪聲兩種干擾信號激勵下的自激振動，詳細研究了主動抑振實驗中抑振穩(wěn)定時間和抑振穩(wěn)定振幅兩項重要指標，最終結論如下。

（1）通過建立MFC 的壓電效應方程和理論推導，驗證了MFC 作為致動器和傳感器的可行性。采用兩種規(guī)格的MFC 分別作為致動器和傳感器，基于應變能最大理論，獲到了MFC 的最佳粘貼位置，得到的控制效果更好。

（2）將PID 自整定的控制算法應用于帆板的振動主動控制中，提高了系統(tǒng)開發(fā)效率，減小了控制算法對帆板模型的依賴。由于帆板柔度較大，振動頻率較低，PID 自整定的響應速度能夠滿足振動抑制的需求。在太空環(huán)境中，PID 自整定具有良好的自我調節(jié)能力，能夠有效防止驅動器失控的情況發(fā)生。

（3）本文設計的系統(tǒng)能夠有效地降低基頻附近的振動，并且在各種外部輸入擾動的情況下，依然能有效地抑制帆板的振動。在自由振動和各種干擾輸入的情況下，引入控制后都能在3～5 s 內進入到平衡狀態(tài)，振動抑制偏差小于3 mm，抑振效率可達4倍以上，抑振效果顯著，達到了預期的效果。