某航空發動機整機系統非線性振動特性分析

林榮洲，侯 磊，，孫傳宗，楊 洋，侯升亮，陳予恕

（1.哈爾濱工業大學航天學院，黑龍江哈爾濱 150001；2.西南交通大學力學與航空航天學院應用力學與結構安全四川省重點實驗室，四川成都 611756；3.沈陽工業大學機械工程學院，遼寧沈陽 110870）

引言

航空發動機作為飛機的動力來源，它的性能直接決定了飛機的性能、可靠性以及成本。但由于航空發動機工作環境復雜，除了受到發動機運轉的不平衡激勵以外，還受到氣動激勵、熱場等的影響，導致航空發動機的振動問題一直是航空領域的重要研究課題［1］。

航空發動機是一種旋轉機械，對于轉子-軸承系統的研究，各個國家的學者已經做出了比較多的研究。Nelson 等［2］就開始運用有限元法對轉子-支承系統進行建模，并計算了該系統的臨界轉速、不平衡響應，驗證了有限元法研究轉子-軸承系統的有效性。隨著非線性振動的興起，轉子轉速的提高，轉子的非線性振動問題也開始受到關注。Ertas 等［3］對一含有平方非線性的2 自由度轉子系統進行了分析，發現了1∶2 內共振、振動突跳等現象，并給出了該系統發生內共振的條件。Young 等［4］運用HB/AFT 方法對含分段非線性的多自由度轉子系統進行了求解，驗證了該方法的準確性。Tiwari 等［5］對支承于球軸承上的剛性轉子進行了分析，考慮了球軸承的Hertz 接觸非線性，發現了軸承間隙以及變剛度會使轉子系統發生倍周期分岔，最后通過實驗驗證了這一結論。Diken［6］對含平方非線性的Jeffcott 轉子進行了分析，發現了非線性可能導致轉子發生亞諧共振。Jing 等［7］建立了考慮油膜力作用的轉子-軸承系統的動力學模型，分析了油膜力對該系統的分岔特性的影響，發現在轉速下降時，會發生油膜渦動和油膜振蕩交換的現象。Hou 等［8-9］研究了機動飛行條件下轉子-球軸承系統的非線性振動響應，發現在機動飛行條件下系統產生了亞諧共振，并且發現在特定轉速時會發生周期1 與周期2 運動交換、周期2 運動與概周期運動交換的現象。

對于轉子系統的動力學特性研究，還包括軸承故障［10-12］、碰摩［13-17］等問題，也取得了許多成果。但現代航空發動機為了滿足高速、高推重比的要求，多采用雙轉子結構。航空發動機的雙轉子結構較為復雜，雙轉子靠中介軸承連接，并且雙轉子通過軸承與機匣連接，最終機匣再與飛行器連接。而對于這樣一個復雜結構，從整機振動的角度去考慮是十分必要的。在航空發動機整機振動方面，國外有一些成果，Bonello 等［18］對含有擠壓油膜阻尼器的航空發動機整機系統進行動力學建模，引入了導納諧波平衡法（RHBM）對整機系統進行分析，將該方法與傳統的脈沖響應法對比，發現導納諧波平衡法對整機系統的非線性動力學分析是很有效的。國內對整機振動也有豐富的研究，洪杰等［19］、于平超等［20］針對高推重比渦扇發動機的質點動載荷振動響應及優化設計問題，建立了轉子系統支點動載荷力學模型，研究了不平衡力以及輪盤慣性載荷等因素對支點動載荷的影響，結果表明通過優化高壓渦輪后軸頸結構能有效減小中介支點動載荷大小。張大義等［21］、Yu 等［22］將有限元法與振型篩選法結合，提出了適用于工程應用的臨界轉速求解方法，并驗證了其準確性。王儼剴，廖明夫等［23-25］通過對3 種典型航空發動機中介軸承各30 臺份的試車數據統計，得到使中介軸承免受“同步沖擊”的原則；同時提出將發動機的健康狀態量化，將模糊綜合評價方法應用于發動機健康狀態等級的評估；最后通過對兩組發動機故障模擬實驗器振動數據的等級評價結果對比，驗證了該方法的有效性。陳果［26-29］考慮了航空發動機整機系統轉子與軸承和機匣的耦合效應，擠壓油膜阻尼器等多種因素，建立了轉子-球軸承-機匣耦合系統的動力學模型，運用Newmark-β 法和翟方法相結合進行求解，得到了整機系統的臨界轉速、不平衡響應，著重分析了擠壓油膜阻尼器對整機系統的振動特性的影響，最終用實驗驗證了模型的準確性。周海侖等［30］以雙轉子航空發動機為研究對象，建立了航空發動機雙轉子-滾動軸承-機匣耦合動力學模型，用龍格-庫塔法進行求解，結果表明，碰摩故障下，整機系統可能從概周期演變為混沌。孫傳宗等［31］以機匣-雙轉子試驗臺為研究對象，用ANSYS 建立了高精度的實體有限元模型，運用Craig-Bampton 模態綜合法實現了子模型維度縮減，最后通過實驗驗證了該方法的準確性。

可以看出對于航空發動機轉子部分非線性振動特性的研究已經很豐富了，但航空發動機的信號監測的測點一般都位于機匣上，轉子部分的各類振動行為在機匣上是何種表現形式的問題卻鮮有研究。因此，本文以某型號航空發動機整機振動試驗臺為研究對象，運用有限單元法建立簡化的整機系統動力學模型，并考慮中介軸承的Hertz 接觸非線性彈性恢復力，結合Newmark-β 法與Newton-Raphson 法進行數值求解，著重研究中介軸承間隙對整機系統非線性振動響應的影響規律，并分析高低壓轉子上的各類非線性振動現象在機匣上不同位置測點的表現形式，進而討論航空發動機機匣上的測點安排。

1 整機系統動力學建模

1.1 基本假設

某型號航空發動機雙轉子結構圖如圖1所示，該發動機共有6 個支點，其中1#，2#，6#為低壓轉子支點，3#和5#為高壓轉子支點，4#為連接高低壓轉子的中介軸承。

圖1 航空發動機雙轉子結構圖Fig.1 Structure diagram of aeroengine dual-rotor

參照文獻［32-33］中的結構簡化方法，將高低壓轉子的轉盤通過質量集中和慣性等效進行合并簡化，同時將機匣簡化為等截面圓柱筒，進而建立了航空發動機整機系統的簡化模型，如圖2所示。圖中坐標原點o在低壓轉子壓氣機頂端處，坐標軸oz與高低壓轉軸的中心線重合。模型中低壓壓氣機部分等效為2 個輪盤L1 和L2，1 個低壓渦輪部分等效為1 個輪盤L3，高壓壓氣機部分等效為1 個輪盤H1，高壓渦輪部分等效為1 個輪盤H2。在輪盤與支承處劃分節點，將低壓轉子劃分為8 個節點，高壓轉子劃分為7 個節點，內涵道機匣劃分為5 個節點，外涵道機匣劃分為6 個節點，其中節點Ⅰ，Ⅱ，Ⅲ依次為機匣的前測點、中測點以及后測點。

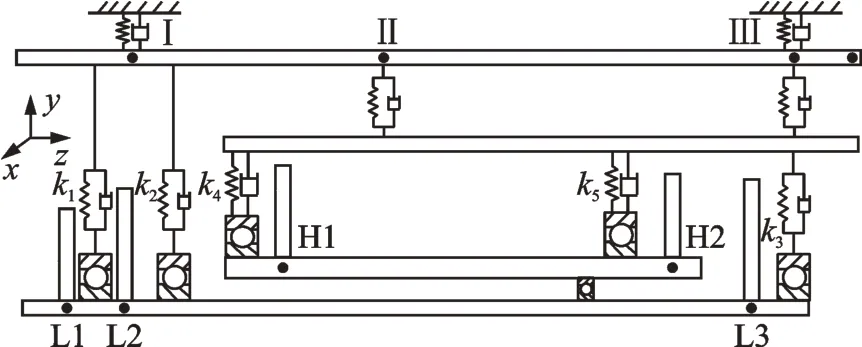
圖2 航空發動機整機系統結構簡圖Fig.2 Structure diagram of overall aeroengine system

建模時考慮的假設如下：

（1）高、低壓壓氣機和高、低壓渦輪的輪盤都考慮為具有回轉效應的剛性圓盤。

（2）轉軸簡化為等截面的空心梁，不考慮轉軸的扭轉與軸向運動的影響，主要考慮轉子的橫向彎曲運動。

（3）支承剛度視為彈性支承和軸承支承的組合剛度，而中介軸承則考慮滾子的Hertz 接觸非線性。

（4）假設在工作轉速內機匣的截面不變形，保持為圓形截面，但機匣軸線有彎曲模態，將機匣處理為不旋轉的等截面空心梁。

運用有限元法對整機系統進行動力學建模［34］，首先將整機系統分為雙轉子系統與機匣，分別建立了雙轉子與機匣的動力學方程后，再將其組裝為整機系統。

對于低壓轉子有L個節點，高壓轉子有H個節點，機匣有C個節點，總共有N個節點的航空發動機整機系統，可以設其位移向量為：

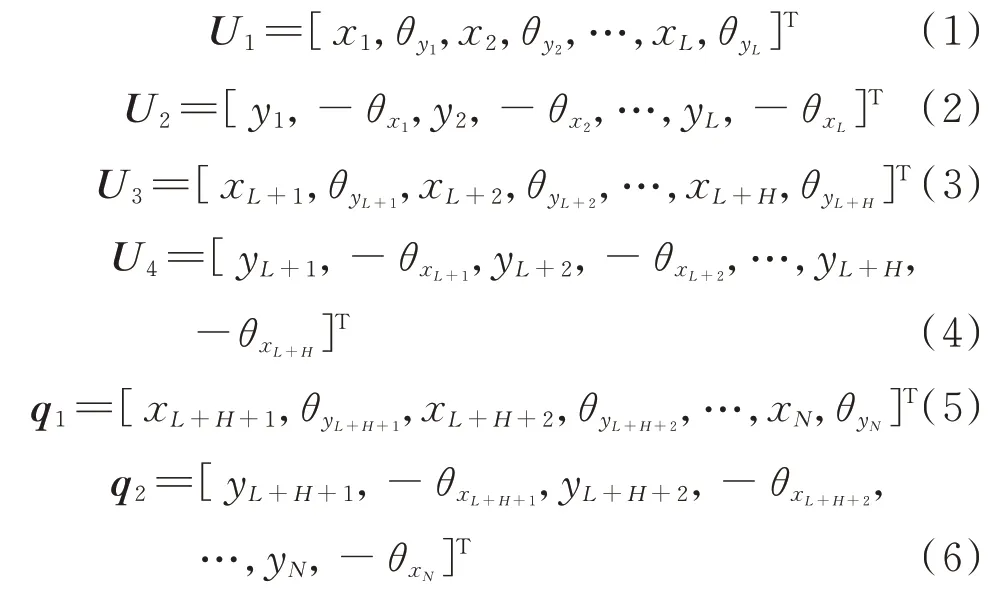
式中U1，U2分別表示低壓轉子的廣義位移向量；U3，U4分別表示高壓轉子的廣義位移向量；q1，q2分別表示機匣軸心的廣義位移向量。

1.2 剛性圓盤、彈性軸段和彈性支承的建模

通過列寫各單元的運動方程，可以得出各個單元的質量矩陣、慣性矩陣和剛度矩陣。其中，剛性圓盤的質量矩陣Md和慣性矩陣J可以表示為：

式中m為圓盤質量；Jd，Jp分別為圓盤的直徑轉動慣量和極轉動慣量。

彈性軸段的質量矩陣Mz、慣性矩陣Jz和剛度矩陣Kz分別表示為：

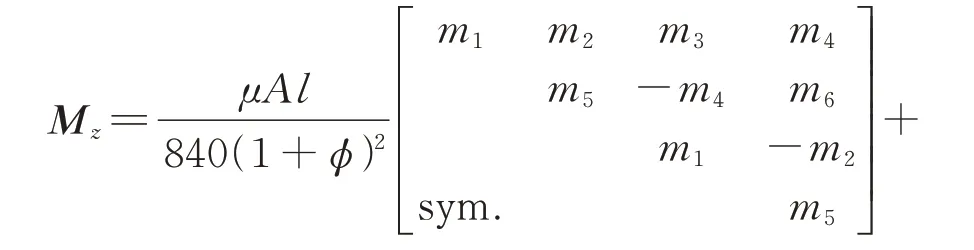
式中μ為軸段密度，l為軸段長度，A為軸段截面面積，E為楊氏模量，Iz為軸段慣性矩。m1=312+588φ+280φ2，m2=(44+77φ+35φ2)l，m3=108+252φ+140φ2，m4=-(26+63φ+35φ2)l，m5=(8+14φ+7φ2)l2，m6=-(6+14φ+7φ2)l2，m7=36，m8=(3-15φ)l，m9=(4+5φ+10φ2)l2，m10=(-1+5φ+5φ2)l2，，κ為剪切修正系數。

1.3 彈性支承及中介軸承的建模

彈性支承的剛度矩陣可以表示為：

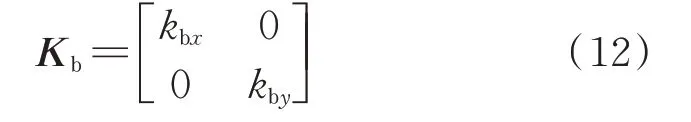
式中kbx，kby別為軸承座x，y兩個方向的剛度，并且一般情況下kbx=kby。

中介軸承位于高低壓轉子之間，軸承內圈與低壓轉子相連，軸承外圈與高壓轉子相連，則中介軸承恢復力在x，y方向的投影可以表示為：

式中Cb為接觸剛度系數，H(·)為Heaviside 函數。δei，θei為第i個滾動體與滾道接觸時的變形及第i個滾動體的位置，分別表示為：

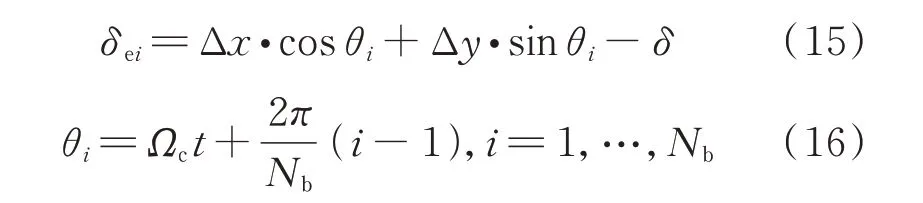
式中 Δx，Δy分別表示內圈中心以及外圈中心在x，y方向上的相對位移；δ為中介軸承的間隙。Nb為滾動體個數；Ωc為保持架轉速。

1.4 整機系統動力學方程的組裝

將機匣考慮為不會旋轉的梁進行建模，則它具有和彈性軸段相同的質量矩陣和剛度矩陣，但不具有慣性矩陣。通過綜合各個單元的運動方程，以節點位移相容的原則，對剛度矩陣、慣性矩陣和質量矩陣進行拼合，最終可以得到系統的運動方程。

獨立的低壓轉子、高壓轉子、機匣的無阻尼自由振動方程依次如下：

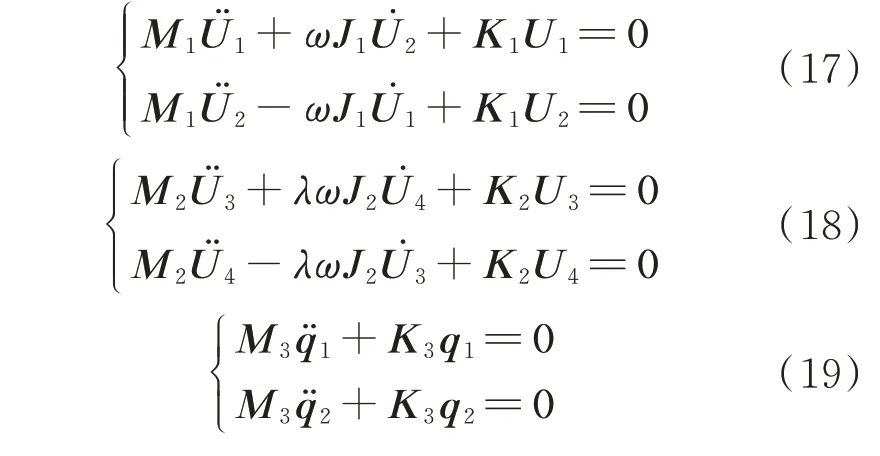
式中M，J，K分別代表拼合的質量矩陣、慣性矩陣、剛度矩陣；下標1，2，3 依次代表的是低壓轉子、高壓轉子、機匣；λ代表高低壓轉子轉速比，本文中取高低壓轉速比為1.2；ω代表低壓轉子自轉角速度。

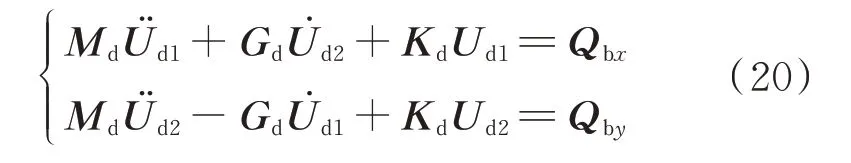
式中Qbx，Qby包含了中介軸承引起的非線性恢復力Fbx，Fby以及施加于轉盤上的不平衡激勵力依次表示施加于第i個轉盤上不平衡激勵在x，y方向上的投影；mi，ωi，δri依次表示第i個轉盤的質量、轉盤對應轉子的轉速以及轉盤的偏心距。本文施加于轉盤上的偏心距如下表1所示。表中轉盤編號與圖2 相對應，L1 和L2 為低壓壓氣機盤，L3 為低壓渦輪盤，H1 為高壓壓氣機盤，H2 為高壓渦輪盤。而偏心距為圓盤質心相對于圓盤幾何中心的偏移量。

表1 轉子偏心距Tab.1 Eccentricity of rotor

再以類似方式將式（18）與（19）組合，此時轉子與機匣剛度矩陣非對角線上應含有耦合剛度。則可以得到整機系統的無阻尼動力學方程：

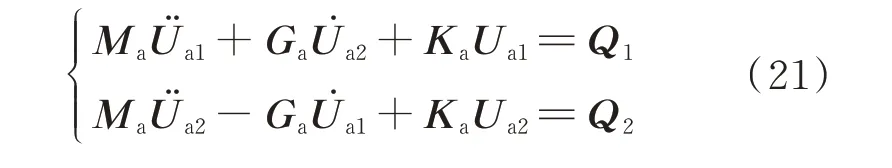
式中Ma，Ga，Ka分別為整機系統的質量矩陣、陀螺矩陣以及剛度矩陣，Ua為整機系統廣義位移，Q為整機系統廣義力，其中下標1表示x方向，下標2表示y方向。

再考慮整機受比例阻尼Ca=αMa+βKa作用，其中α，β為比例阻尼系數，可以通過下式確定：

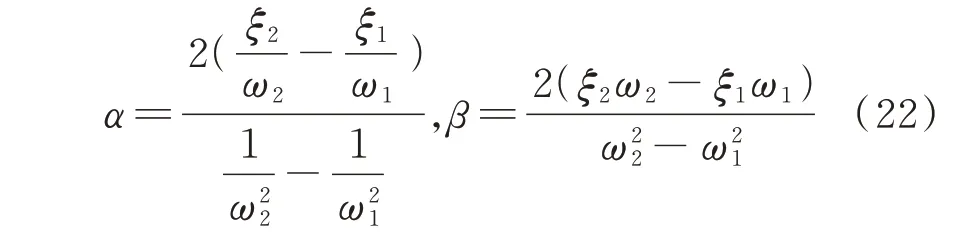
式中ξ1，ξ2為模態阻尼比；ω1，ω2為整機系統的第1階和第2 階臨界轉速。

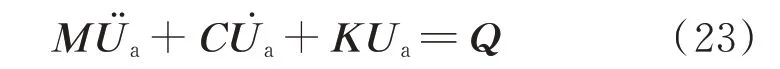
為了了解整機系統的固有特性，不妨先參照文獻［35］近似計算中介軸承徑向剛度如下式所示：

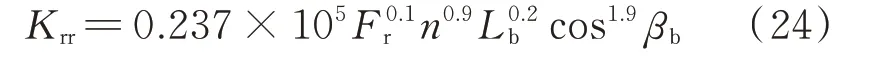
式中d為滾珠直徑，Lb為滾子有效長度，n為滾子數目，βb為接觸角，Fr為徑向外力，本文中為軸承所承受的軸段和盤的重力。

利用式（24）進而將中介軸承等效線性化。然后求解式（23）的廣義特征值問題，可以得到整機系統線性化條件下的臨界轉速與振型，其中前兩階臨界轉速依次為772，1649.7 rad/s，對應的前兩階振型如圖3所示。可以看出第1 階振型為高壓渦輪盤的振動，低壓轉子由于中介軸承的作用也會有一些振動。第2 階振型為低壓壓氣機盤的振動。

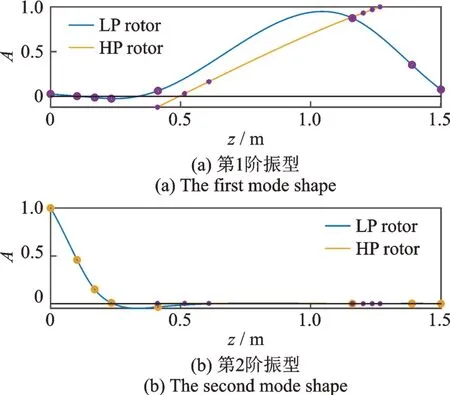
圖3 整機系統前2 階振型Fig.3 The first 2 mode shapes of overall aeroengine system

同時為了驗證模型的準確性，通過商業有限元軟件建立了高精度的有限元模型，同樣計算其臨界轉速與振型，其前2 階臨界轉速對比如表2所示，可以看出簡化后臨界轉速誤差不超過10%；而商業有限元軟件振型如圖4所示，簡化前后振型不變，驗證了模型的準確性。

表2 整機系統臨界轉速對比Tab.2 Comparison of critical speed of overall aeroengine system

圖4 高精度有限元模型計算的整機系統前2 階振型Fig.4 The first 2 mode shapes of overall aeroengine system using high accuracy finite element model

2 中介軸承間隙對高低壓轉子非線性振動特性的影響

采用Newmark-β 與Newton-Raphson 結合的方法［36-37］進行數值求解，可以得到整機系統各個節點的位移響應。由于航空發動機為雙轉子結構，因而存在雙頻不平衡激勵，其振動響應中存在至少兩種頻率成分。為了更清晰地反映振動的強度，本文采用振動信號能量的有效值［38］來表示常規幅頻曲線中的振幅：

式中x（t），y（t）為系統節點對應方向的位移響應；T為高、低壓轉子不平衡激勵周期的公倍數，不妨稱其為公共周期；xˉ，yˉ為公共周期T內的位移相應響應平均值；N為公共周期T離散的總點數，可以畫出以有效值A為幅值的幅頻響應圖。

中介軸承間隙是中介軸承的關鍵參數，它的大小會很明顯地影響整機系統的動力學特性。圖5給出了中介軸承不同間隙下低壓轉子壓氣機1盤的幅頻響應曲線，其中ω為低壓轉子的轉速，圖中實線是升速曲線，虛線是降速曲線。由于中介軸承非線性，因此該條件下的第1階臨界轉速與線性化條件下計算的臨界轉速并不完全相等。由圖可知，在高低壓轉速比λ為1.2，整機系統在第1 階臨界轉速下（760 rad/s）時，低壓壓氣機1盤并未出現共振峰，由圖3（a）可知，整機系統第1階臨界轉速對應的振型是高壓轉子渦輪盤的振動，且由于低壓壓氣機1盤是一個懸臂結構，它的幅頻響應沒有明顯的共振峰出現，只有幅值隨著不平衡響應的增大而增大。并且增大中介軸承間隙對低壓壓氣機1盤的振動特性沒有顯著影響。

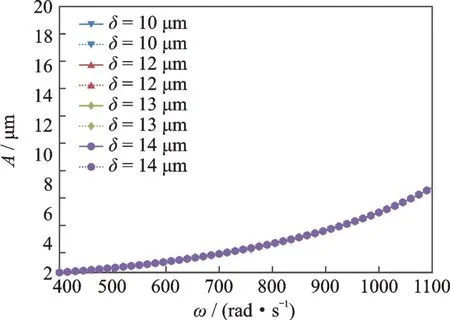
圖5 低壓壓氣機1 盤幅頻響應曲線（實線為升速曲線，虛線為降速曲線）Fig.5 Amplitude-frequency response of low pressure compressor disk L1（full lines are run up，dotted lines are slow down）

低壓轉子壓氣機2 盤和低壓轉子渦輪的幅頻響應分別如圖6 和7所示。可以看出，在第1 階臨界轉速下有兩個共振峰，第1 個共振峰對應的低壓轉子轉速633.3 rad/s，該共振峰是由高壓轉子不平衡激勵引起的，第2 個共振峰對應的轉速是760 rad/s，是低壓轉子不平衡激勵引起的。由于高壓轉子轉速大于低壓轉子的轉速，因此高壓轉子先通過第1 階臨界轉速，低壓轉子后通過。

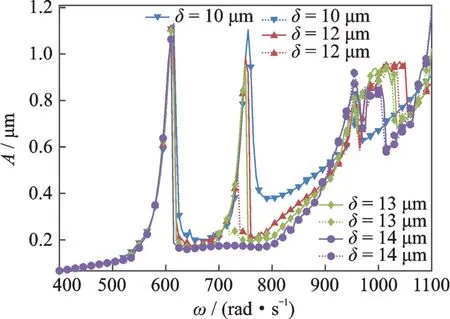
圖6 低壓壓氣機2 盤幅頻響應曲線（實線為升速曲線，虛線為降速曲線）Fig.6 Amplitude-frequency response of low pressure compressor disk L2（full lines are run up，dotted lines are slow down）

高壓轉子壓氣機與渦輪的幅頻響應分別如圖8和9所示。高壓轉子的情況與低壓轉子的情況相類似，但高壓轉子渦輪的振幅大于低壓轉子渦輪的振幅，高壓壓氣機的振幅也大于低壓壓氣機的振幅，這是因為此時的振型是高壓轉子渦輪的振動，而通過中介軸承的傳遞，低壓轉子渦輪也有較大的振動，高壓壓氣機與低壓壓氣機則振動較小。

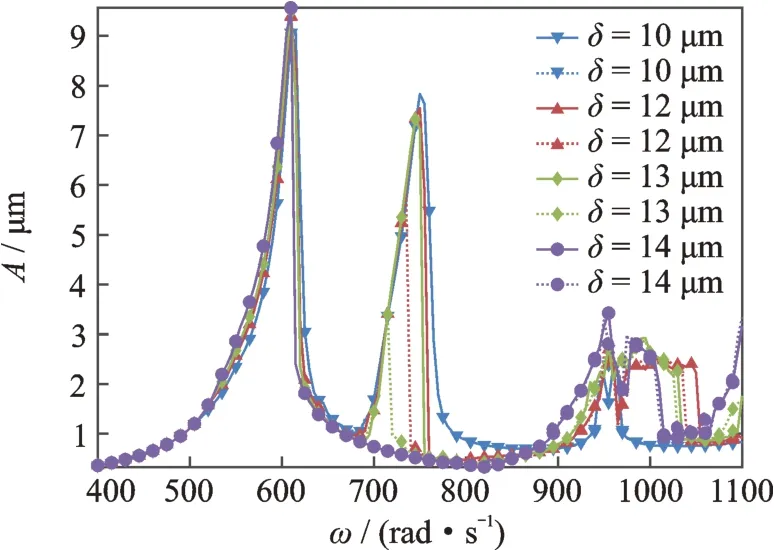
圖8 高壓壓氣機幅頻響應曲線（實線為升速曲線，虛線為降速曲線）Fig.8 Amplitude-frequency response of high pressure compressor disk H1（full lines are run up，dotted lines are slow down）

圖7 低壓渦輪幅頻響應曲線（實線為升速曲線，虛線為降速曲線）Fig.7 Amplitude-frequency response of low pressure turbine disk L3（full lines are run up，dotted lines are slow down）

同時注意到，對于除了低壓壓氣機1 盤以外的部位，如圖6～9所示，當中介軸承間隙δ=12 μm 時，第2 個共振峰均出現了振動突跳現象，但第1 個共振峰則并未出現這一現象。同時在系統升速過程中跳躍點與降速過程中跳躍點之間形成了雙穩態區間，當增大間隙時，兩個共振峰對應的臨界轉速都有略微的減小，兩個共振峰對應的幅值也略有減小，其中第2 個共振峰的減小幅度大于第1 個共振峰。對于雙穩態區間而言，增大中介軸承間隙，第1 個共振峰還是沒有出現雙穩態現象，而第2 個共振峰的雙穩態區間開始增大。

當繼續增大中介軸承間隙，達到δ=14 μm 時，幅頻響應圖中第2 個共振峰“消失”。為了繼續探究這一現象，分別給出間隙δ=10，14 μm 的情況下高壓轉子渦輪與低壓轉子渦輪處的時間歷程圖、頻譜圖以及軸心軌跡圖，如圖10 和11所示。可以看出，在δ=10 μm 時，高、低壓轉子渦輪的頻譜中既有高壓轉子不平衡激勵頻率Ω2=λω，也有低壓轉子不平衡激勵頻率Ω1=ω，并且低壓轉子不平衡激勵頻率的幅值較大，表明該共振峰主要是由低壓轉子不平衡激勵激起的。從軸心軌跡圖可以看出此時的軸心軌跡為高低壓轉子的耦合，是一些圓的交錯疊加。

圖10 低壓渦輪在ω=760 rad/s，δ=10 μm 下的時間歷程圖、軸心軌跡圖與頻譜圖Fig.10 Time history，orbit of shaft and frequency spectrum of low pressure turbine at ω=760 rad/s，δ=10 μm

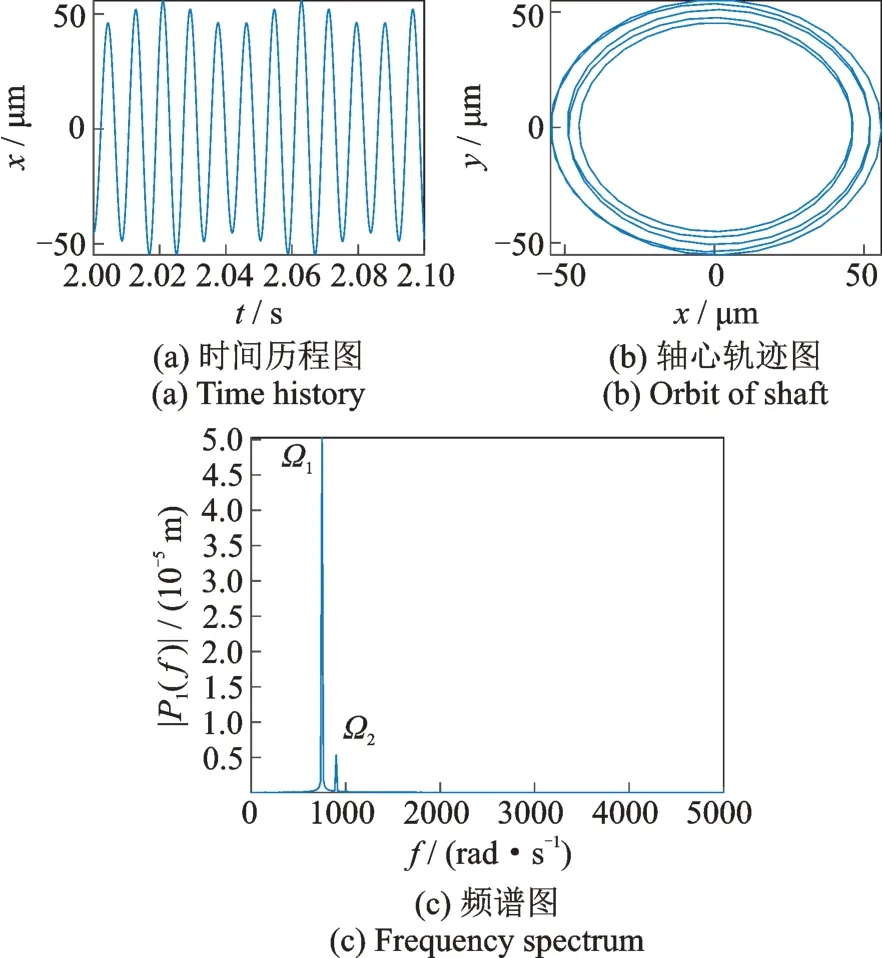
圖11 高壓渦輪在ω=760 rad/s，δ=10 μm 下的時間歷程圖、軸心軌跡圖與頻譜圖Fig.11 Time history，orbit of shaft and frequency spectrum of high pressure turbine at ω=760 rad/s，δ=10 μm

如圖12 和13所示，在δ=14 μm 時，低壓轉子渦輪處的頻譜中的低壓轉子不平衡激勵頻率Ω1為主要頻率成分，高壓轉子不平衡激勵頻率Ω2只有很少的貢獻。而高壓轉子渦輪處的頻譜則情況相反，此時高壓轉子不平衡激勵頻率Ω2為主要頻率成分，而Ω1的貢獻很小，說明此時高低壓轉子各自運動，幾乎沒有耦合作用。由圖3（a）可知，系統第1 階振型為高壓轉子的振動，因而低壓轉子的不平衡激勵并不能有效傳遞到高壓轉子，因此低壓轉子激起的共振峰“消失”。從軸心軌跡可以看出此時低壓轉子與高壓轉子的軸心軌跡都為比較規則的單圓環的疊加。

圖12 低壓渦輪在ω=760 rad/s，δ=14 μm 下的時間歷程圖、軸心軌跡圖與頻譜圖Fig.12 Time history，orbit of shaft and frequency spectrum of low pressure turbine at ω=760 rad/s，δ=14 μm

因此，當中介軸承間隙增大到一定程度（δ=14 μm）時，會發生滾動體與滾道不接觸的現象，導致高低壓轉子的耦合程度降低甚至于“脫離”，在達到相應的臨界轉速時，低壓轉子的不平衡激勵并不能有效地傳導到高壓轉子使之發生共振。

此外，如圖9所示，當中介軸承間隙δ=10 μm時，高壓渦輪的幅頻響應在低壓轉子轉速為950 rad/s 處出現了一個共振峰。為了分析這一現象，分別給出了δ=1，5 和10 μm 時，低壓轉子轉速ω=950 rad/s，高低壓轉速比λ=1.2 情況下，高低壓轉子渦輪處的時間歷程圖、頻譜圖以及軸心軌跡圖，如圖14～16所示，其中（a）～（c）依次為低壓轉子渦輪的時間歷程、頻譜圖和軸心軌跡圖，（d）～（f）依次為高壓轉子渦輪的時間歷程、頻譜圖和軸心軌跡圖。

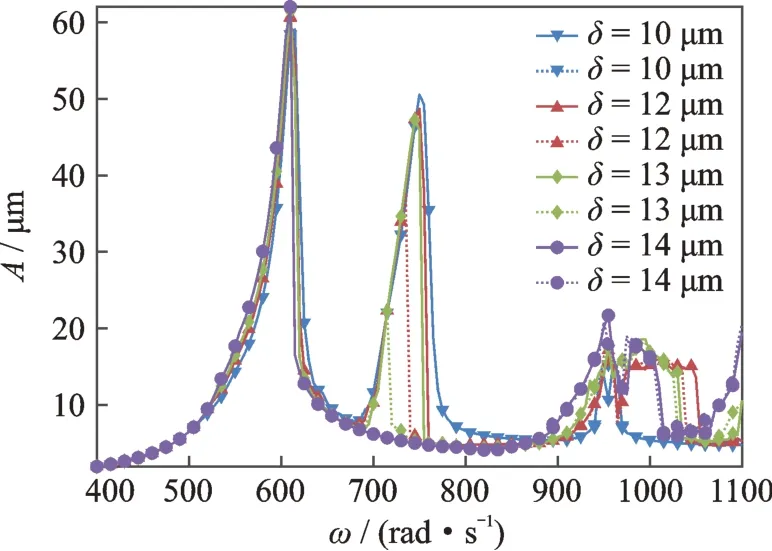
圖9 高壓渦輪幅頻響應曲線（實線為升速曲線，虛線為降速曲線）Fig.9 Amplitude-frequency response of high pressure turbine disk H2（full lines are run up，dotted lines are slow down）

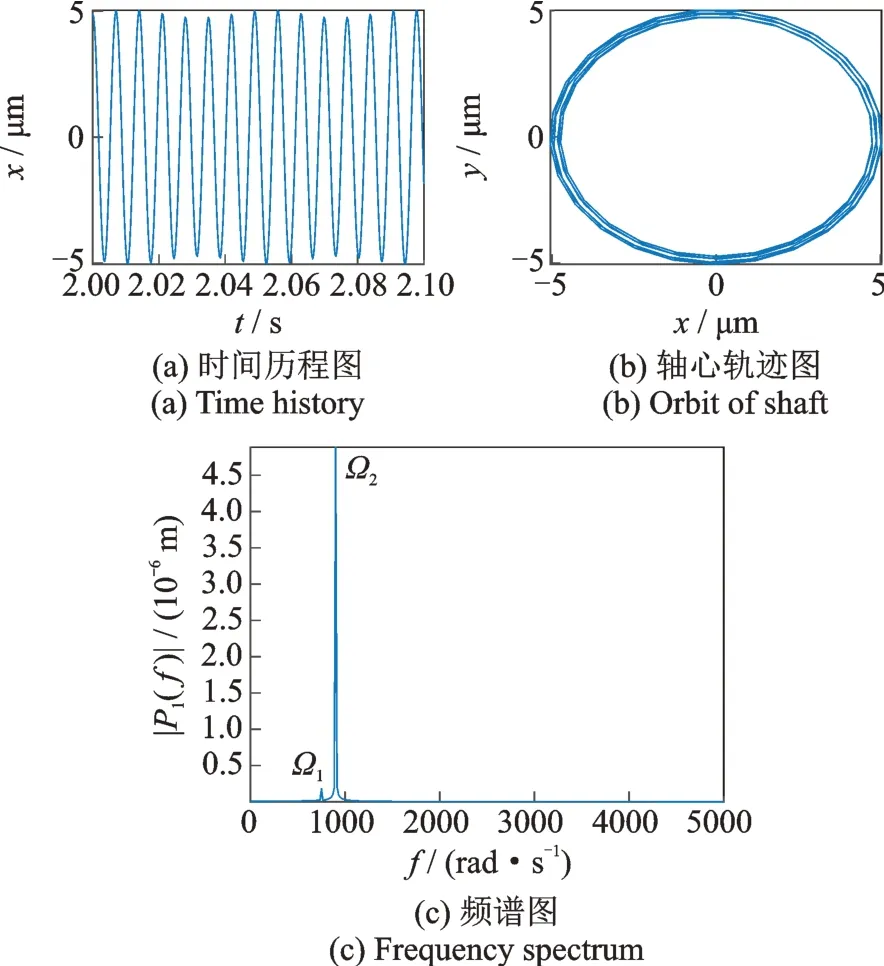
圖13 高壓渦輪在ω=760 rad/s，δ=14 μm 下的時間歷程圖、軸心軌跡圖與頻譜圖Fig.13 Time history，orbit of shaft and frequency spectrum of low pressure turbine at ω=760 rad/s，δ=14 μm

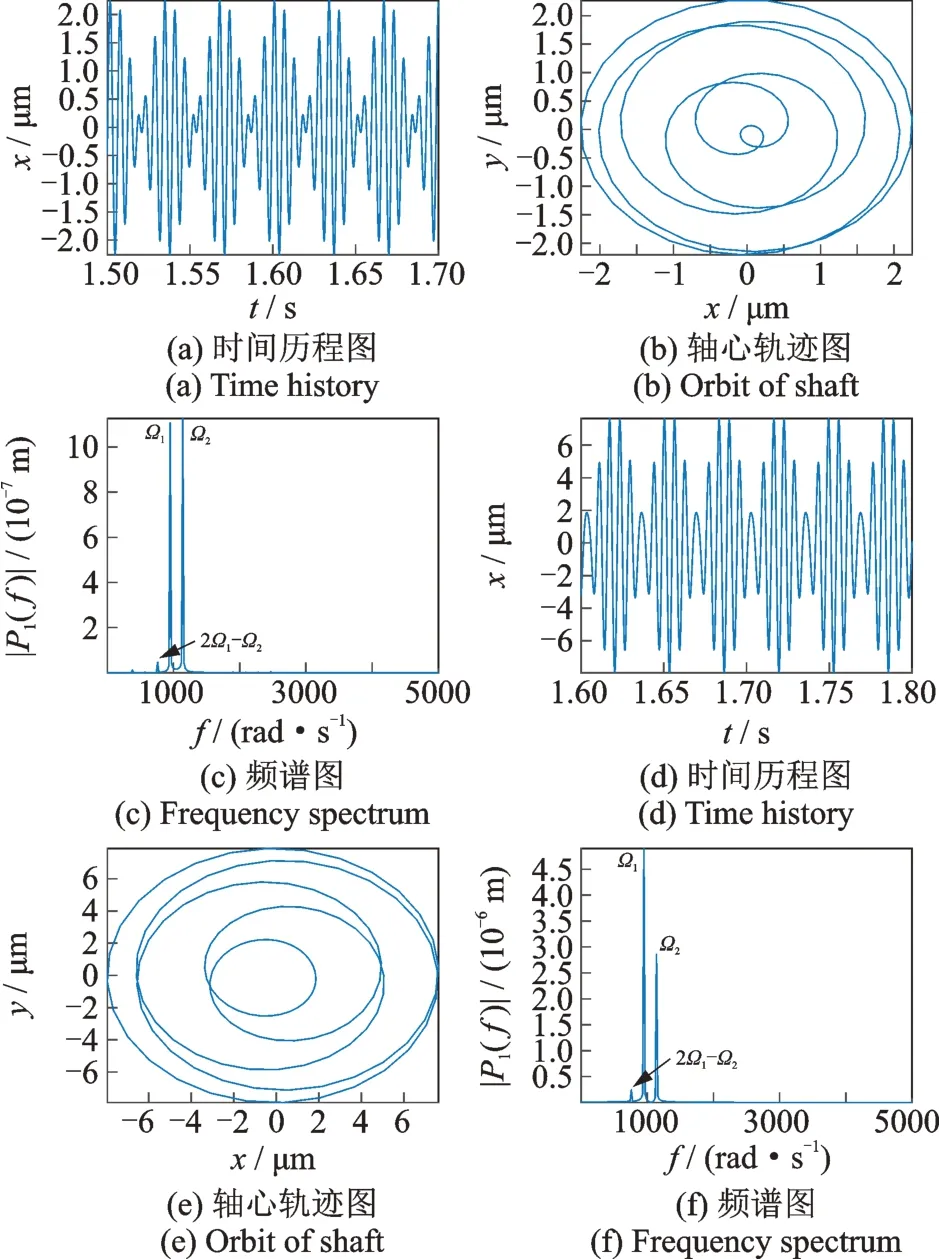
圖14 低壓渦輪（a）～（c）與高壓渦輪（d）～（f）在ω=950 rad/s，δ=1 μm 下的時間歷程圖、軸心軌跡圖與頻譜圖Fig 14 Time history，orbit of shaft and frequency spectrum of low pressure turbine（a）～（c）and high pressure turbine（d）～（f）at ω=950 rad/s，δ=1 μm

由圖14 可知，當δ=1 μm 時，高低壓轉子渦輪處均分別以高低壓轉子的不平衡激勵頻率Ω1，Ω2占主導，組合頻率2Ω1-Ω2的作用很微弱，此時的軸心軌跡為相疊加的圓環。由圖15 可見，當增大間隙時（δ=5 μm），除了高低壓轉子的不平衡激勵Ω1，Ω2外，組合頻率2Ω1-Ω2的作用開始變得明顯，而高壓轉子的不平衡激勵Ω2引起的幅值開始減小。由圖16 可見，在δ=10 μm 時，除了2Ω1-Ω2以外，還出現了Ω2-Ω1，2Ω2-2Ω1，2Ω2-Ω1等組合頻率成分，其中，高低壓渦輪的情況有所不同：低壓渦輪此時仍然以低壓不平衡激勵Ω1為主導，而高壓渦輪則是以組合頻率2Ω1-Ω2為主導，通過計算可知，此時組合頻率2Ω1-Ω2的值為760 rad/s，與整機系統第一階臨界轉速760 rad/s 重合，因此950 rad/s 位置處的共振峰為組合頻率2Ω1-Ω2引起的組合共振。此外，低壓渦輪中組合頻率Ω1+Ω2的作用較明顯，而高壓渦輪中組合頻率Ω1+Ω2的成分十分微弱。另外，高低壓渦輪的軸心軌跡隨著中介軸承間隙的增加都變得較為混亂。

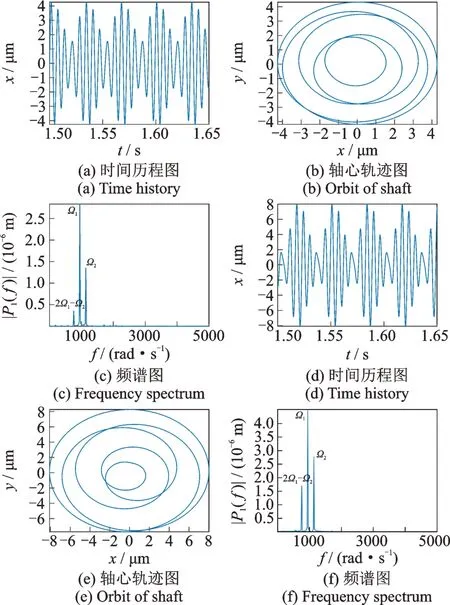
圖15 低壓渦輪（a）～（c）與高壓渦輪（d）～（f）在ω=950 rad/s，δ=5 μm 下的時間歷程圖、軸心軌跡圖與頻譜圖Fig.15 Time history，orbit of shaft and frequency spectrum of low pressure turbine（a）～（c）and high pressure turbine（d）～（f）at ω=950 rad/s，δ=5 μm

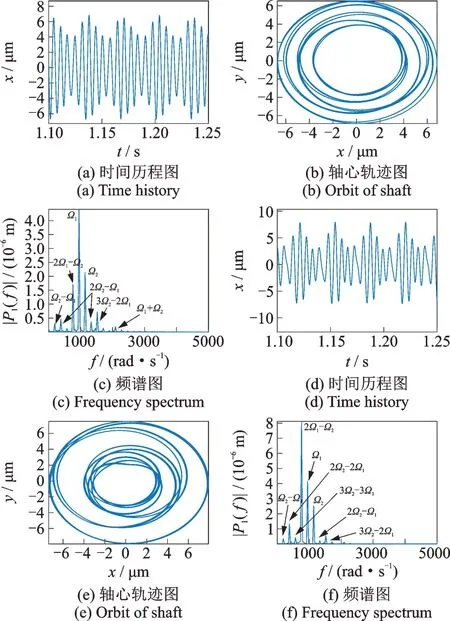
圖16 低壓渦輪（a）～（c）與高壓渦輪（d）～（f）在ω=950 rad/s，δ=10 μm 下的時間歷程圖、軸心軌跡圖與頻譜圖Fig.16 Time history，orbit of shaft and frequency spectrum of low pressure turbine（a）～（c）and high pressure turbine（d）～（f）at ω=950 rad/s，δ=10 μm

3 中介軸承間隙對機匣非線性振動特性的影響

中介軸承的間隙對于雙轉子的非線性振動特性有較為明顯的影響，但在實際的航空發動機中，難以直接監測到轉子的信號，往往只能在機匣上布置測點，那么機匣上的信號是否能夠切實地反映內部雙轉子的現象以及機匣測點的位置是否對監測效果有影響都是值得考慮的問題。

機匣前測點Ⅰ的幅頻響應如圖17所示，對比機匣前測點和高低壓轉子的幅頻響應曲線（如圖5～9），可以看出機匣的振動的幅值相較于轉子而言小2 個數量級，因此機匣上的信號其實是十分微弱的，但是機匣前測點的振動響應隨著中介軸承間隙的變化規律與高低壓轉子的規律相類似：當中介軸承間隙增大時，臨界轉速略微減小，雙穩態區間增大，共振峰幅值略微減小，其中第2 個共振峰減小的幅度比第1 個共振峰大；當中介軸承間隙δ=14 μm 時，第二個共振峰消失。但是在高低壓轉子出現組合頻率的轉速下，前測點組合共振峰峰值很小。做出機匣前測點在ω=950 rad/s，δ=10 μm 時的時間歷程曲線以及頻譜圖如圖18所示，可以發現此時機匣前測點雖然有組合頻率成分2Ω1-Ω2，但該頻率成分并未占據主導地位，此時前測點的振動主要是受到低壓轉子不平衡激勵Ω1的影響，在對應的轉速下，并不能反映內部雙轉子的所有組合頻率。

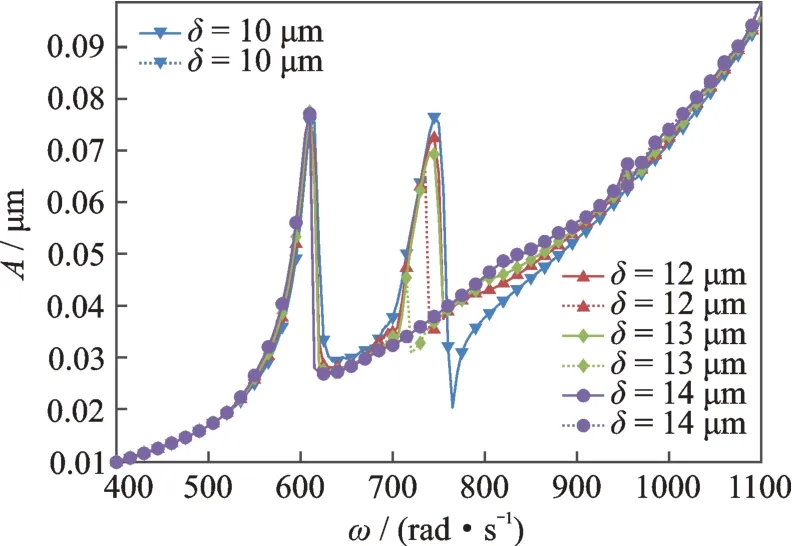
圖17 機匣前測點Ⅰ的幅頻響應圖（實線為升速曲線，虛線為降速曲線）Fig.17 Amplitude-frequency response of front casing pointⅠ（full lines are run up，dotted line are slow down）

圖18 機匣前測點Ⅰ在ω=950 rad/s，δ=10 μm 下的時間歷程圖與頻譜圖Fig.18 Time history and frequency spectrum of front casingpointⅠat ω=950 rad/s，δ=10 μm

機匣中測點和后測點的幅頻響應分別如圖19，20所示，可以發現中后測點的幅頻響應規律較為相似，能夠體現出高低壓轉子振動響應的相應規律，且振動的幅值是比前測點大的。并且在低壓轉子轉速950 rad/s 的條件下，也出現了較明顯的組合共振峰。繪出機匣中測點與后測點在ω=950 rad/s，δ=10 μm 時的時間歷程曲線及頻譜圖，分別如圖21 和22所示。可以發現中測點的頻譜圖與高壓渦輪的頻譜（圖16（f））相比，都是由組合頻率2Ω1-Ω2占主導作用，但機匣中測點的頻譜中缺少了Ω2-Ω1，3Ω2-3Ω1這兩種頻率成分，卻多出了Ω1+Ω2這一頻率成分，這個頻率成分在低壓渦輪上（圖16（c））能夠觀測到，但不明顯。對比圖21 和22，可以發現機匣后測點相較于機匣中測點也有所不同：首先是機匣中測點的頻率成分中，低壓轉子不平衡激勵頻率Ω1的成分的幅值比高壓轉子不平衡激勵頻率Ω2成分的幅值更大，在后測點則情況相反，高壓轉子不平衡激勵頻率Ω2成分的幅值更大，其次機匣后測點的頻譜圖中相對于中測點缺少了2Ω2-2Ω1這一頻率成分。機匣不同部位對不同頻率成分的敏感度不同，高低壓轉子上的振動傳遞到機匣后一些頻率成分衰減得多，一些頻率成分衰減得少，因此轉子上一些比較明顯的頻率成分在機匣上表現的不明顯，而一些在轉子上不容易觀察到的頻率成分反而在機匣上更明顯。

圖19 機匣中測點Ⅱ幅頻響應圖（實線為升速曲線，虛線為降速曲線）Fig.19 Amplitude-frequency response of middle casing pointⅡ（full lines are run up，dotted line are slow down）

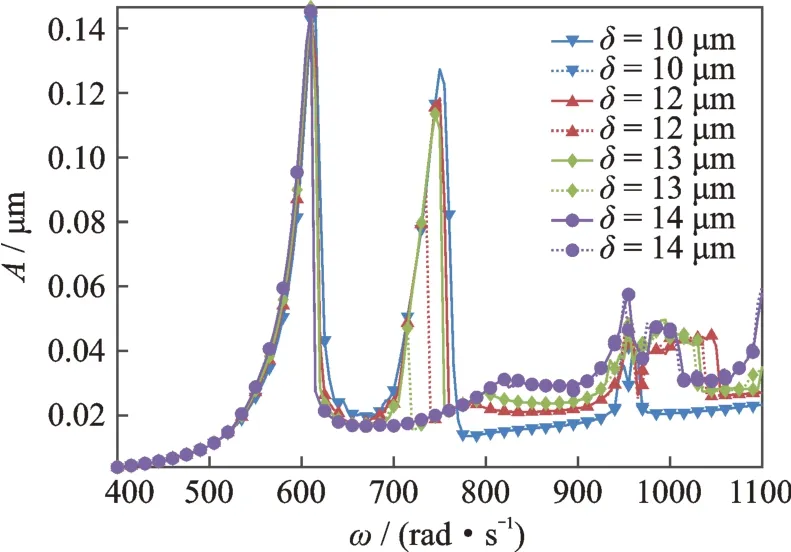
圖20 機匣后測點Ⅲ幅頻響應圖（實線為升速曲線，虛線為降速曲線）Fig.20 Amplitude-frequency response of rear casing pointⅢ（full lines are run up，dotted line are slow down）

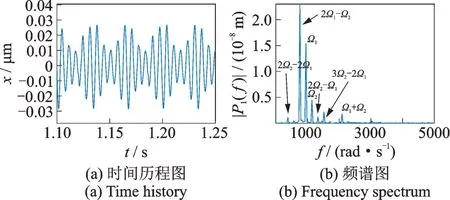
圖21 機匣中測點Ⅱ在ω=950 rad/s，δ=10 μm 下的時間歷程圖與頻譜圖Fig.21 Time history and frequency spectrum of middle casing point Ⅱat ω=950 rad/s，δ=10 μm

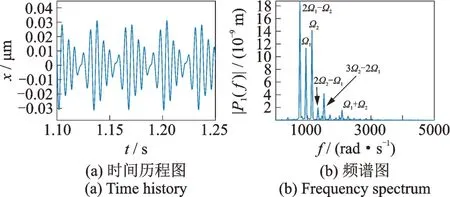
圖22 機匣后測點Ⅲ在ω=950 rad/s，δ=10 μm 下的時間歷程圖與頻譜圖Fig.22 Time history and frequency spectrum of rear casing point Ⅲat ω=950 rad/s，δ=10 μm

綜合對比機匣前中后測點的情況，可以發現機匣測點位置不同所能監測到的現象是不同的，前測點雖然能夠觀察到振動突跳及雙穩態等現象，但在雙轉子內部發生組合共振時，機匣前測點的組合共振峰幅值不明顯，頻率成分少。機匣中后測點在內部雙轉子發生振動突跳、雙穩態及組合共振現象時均有類似現象產生。但中后測點情況也不同，機匣中測點的振動幅值大于機匣后測點，且機匣中測點在組合共振時能監測到的相關組合頻率成分也比機匣后測點的更為豐富。根據以上對比，該機型的機匣測點安排應為機匣中測點最優，機匣后測點其次，最后是機匣前測點。

4 結論

本文以某型號航空發動機整機振動試驗臺為研究對象，考慮了中介軸承Hertz 接觸非線性，建立了簡化的整機系統非線性動力學模型，采用Newmark-β 與Newton-Raphson 結合的方法求解整機系統的非線性振動響應，著重分析了中介軸承間隙對整機系統非線性振動特性的影響規律，主要結論如下：

1）中介軸承的間隙對整機系統的非線性振動特性影響顯著，增大間隙能夠產生豐富的非線性現象。當中介軸承間隙由1 μm 增大到10 μm 時，整機系統振動響應中出現豐富的組合頻率（mΩ1±nΩ2）成分，其中組合頻率2Ω1-Ω2逐漸占據主導地位，進而引發組合共振（低壓轉子轉速950 rad/s）。當中介軸承間隙增加到12 μm，低壓轉子不平衡激勵激起的共振峰會產生振動突跳與雙穩態現象，高壓轉子不平衡激勵激起的共振峰則沒有這些現象。在此基礎上繼續增大間隙時，共振峰幅值會略微減小，共振峰對應的轉速也會略微減小，而雙穩態區間會增大。

2）中介軸承的間隙對高低壓轉子振動的耦合程度有一定影響。增大中介軸承間隙，高低壓轉子的耦合程度會降低，當中介軸承間隙到達14 μm 時，高低壓轉子的耦合程度會極大下降，導致低壓轉子不平衡激勵在第1 階臨界轉速下激起的共振峰“消失”。

3）機匣上的振動信號可以反映出機匣內部高低壓轉子的振動情況，但機匣上不同位置測點的情況不同。當雙轉子出現振動突跳、雙穩態以及組合共振現象時，機匣中后測點均能夠監測到相應的現象，其中機匣中測點能夠監測到的組合頻率更為豐富，且機匣中測點監測到的振動幅值也更大，因此當為本機型選擇布置機匣測點布置時，機匣中測點最優，機匣后測點次之，最后為機匣前測點。

進一步的研究工作將集中在中介軸承間隙對航空發動機整機系統分岔特性的影響問題。并且考慮更為詳細的發動機轉子結構，研究振動信號從高低壓轉子到機匣各測點的振動傳遞路徑問題。