功率譜二次正交化法在隨機地震動響應的應用

葛新廣，龔景海，李創第，3，王昌盛

（1.上海交通大學船舶海洋與建筑工程學院，上海 200240；2.柳州工學院土木建筑學院，廣西柳州 545616；3.廣西科技大學土木建筑學院，廣西柳州 545006；4.黃淮學院建筑工程學院，河南駐馬店 463000）

引言

地震是人類生存面臨的最主要威脅之一，其威脅體現在強烈地震對工程結構的嚴重破壞以及導致的大量人員傷亡和財產損失上。為此，人們對地震的研究由來已久。隨著地震記錄資料的不斷積累和對地震發生規律研究的逐漸深入，地震動的隨機特性成為工程界的共識［1-4］。自Housner［5］首次提出的白噪聲激勵模型以來，各國學者陸續提出了用于模擬地震動隨機性的模型，如Kanai-Tajimi 譜［6-7］、Clough-Penzien 譜［8］、胡聿賢譜［9］、歐進萍譜［10］、李鴻晶譜［11］等。Kanai-Tajimi 譜是首次提出利用基于白噪聲的濾波方程來表示復雜的隨機地震動激勵的模型，而Clough-Penzien 譜、胡聿賢譜、歐進萍譜、李鴻晶譜等又是Kanai-Tajimi 譜的改進模型，因此地震動隨機模型越來越接近實際地震動，但表達式越來越復雜。李鴻晶譜對Kanai-Tajimi 譜中的基巖低頻和高頻范圍同時進行修正，提出了適用性更強的隨機地震動模型，但該模型表達式復雜，濾波方程含有頻域項，傳統方法分析結構地震動響應時結果均較為復雜。目前，鮮有關于李鴻晶譜的工程應用文獻。

結構的隨機振動分析方法分為時域法［12-14］和頻域法［15-18］。在時域法中，結構響應協方差與激勵協方差存在二重積分的關系。因此，時域法應用的前提是隨機激勵要有協方差表達式，且表達式越簡單越容易獲得簡明的響應解。李創第等［19-20］基于復模態方法研究了結構基于Kanai-Tajimi譜或Clough-Penzien 譜的地震動響應，但僅獲得方差且表達式比較復雜。在頻域法中，結構響應的功率譜與激勵的功率譜存在簡明的代數關系，而所有的隨機激勵都是具有功率譜表達式的，因此，該方法應用較為廣泛。矩陣直接譜法［16］、虛擬激勵法［15，21］和傳遞函數法［17-18］都是頻域法中的典型方法。李春祥等［22］利用傳遞函數法研究了MTMD 結構基于Kanai-Tajimi譜或Clough-Penzien 譜的地震動響應特征，但結構地震動響應方差分析采用的方法為數值計算。頻域法中結構響應的0 階譜矩等于其方差，2 階譜矩等于響應變化率的方差，1 階譜矩則是基于首超破壞和Markov 過程假設進行可靠度分析的重要參數［12，23-25］。然而，無論哪種頻域法在獲得結構響應功率譜密度函數之后，都需要數值求解獲得結構響應的譜矩和方差，計算工作量會隨著振動系統的增大而成倍增加。

本文的主要工作有：首先，利用留數原理，給出了李鴻晶譜等效的二次正交式，利用復模態法將結構的二階地震動方程解耦為一階系統的線性組合；其次，利用一階系統的虛擬激勵法建立線性結構系列地震動響應（相對于地面位移及速度、層間相對位移及其變化率）的頻響函數的二次正交式，進而獲得結構系列響應功率譜的二次正交式；最后，基于譜矩的定義及隨機振動理論，獲得了結構地震動系列響應方差和0 階、1 階和2 階譜矩的簡明封閉解。

1 線性結構地震動系列響應頻域解的統一表達式

1.1 線性結構廣義復模態變量的頻域解

對于n層的多、高層線型結構，在地震隨機激勵下的動力方程：

式中M，C和K分別為結構體系的質量、剛度和阻尼矩陣，元素均為常數和分別為結構層相對于地面的位移、速度和加速度向量；I為n×1 階常矩陣，用來定位地震動激勵；為地震動隨機激勵。

目前工程上常用的平穩地震動隨機激勵模型有Kanai-Tajimi 譜［6-7］、Clough-Penzien 譜［8］、胡聿賢譜［9］、歐進萍譜［10］、李鴻晶譜［11］等，它們的功率譜均以有理式的形式表示。其中，李鴻晶譜是一種同時考慮基巖擾動低頻和高頻，較為準確的隨機地震動激勵譜，其表達式為［11］：

式中ωl和ωh分別為控制基巖擾動低頻和高頻成分的參數；ωg和ξg分別為場地基巖上土層的特征頻率和阻尼比；S0為基巖擾動白噪聲的強度。

由式（2）可知，該表達式極其復雜，且該功率譜的濾波方程為非線性的，用時域法無法求解。若采用頻域法，結構地震動響應的譜矩為含有式（2）的積分，只能用數值積分，故存在計算效率和精度的問題。為了獲得結構地震動響應的簡明封閉解，本文基于留數定律［26］提出了李鴻晶譜的等效二次正交式：

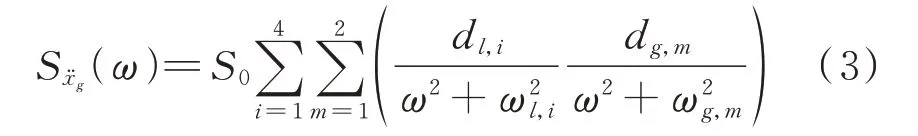
式中

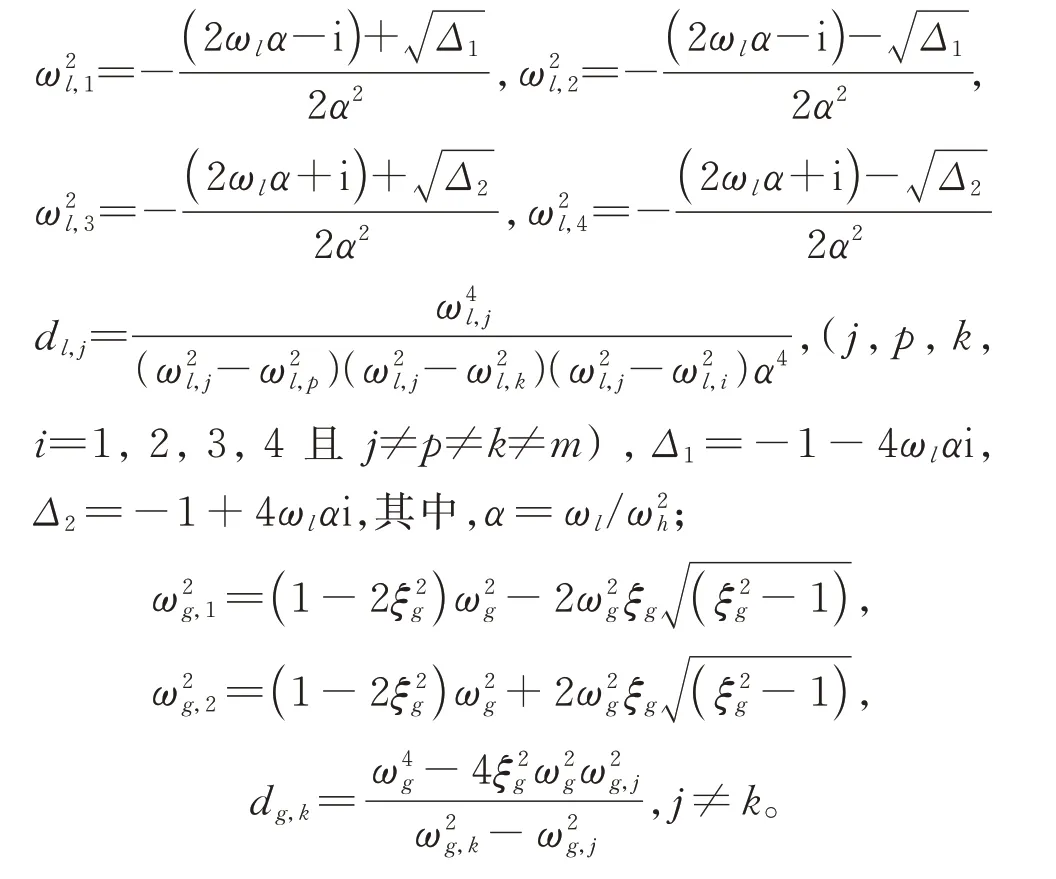
基于隨機激勵下的結構動力響應主要是時域法和頻域法，時域法應用的前提是激勵要有協方差，而被工程界認可的地震動激勵模型都是以功率譜形式提出，時域法應用時所得解均比較復雜；頻域法應用時易于獲得結構動力響應的功率譜，但響應的方差和譜矩的計算為數值法。為此，本文提出了結構頻響函數的二次正交法。為獲得結構頻響函數的二次正交形式，引入狀態變量：

則式（1）改寫為：

式中

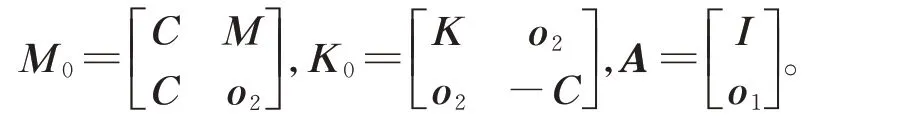
式中o1為元素為0 的n×1 階向量；o2為元素為0的n×n階方陣。

由復模態法理論［12，20］，式（5）存在右、左特性向量矩陣U，V和特征值矩陣P，并滿足：

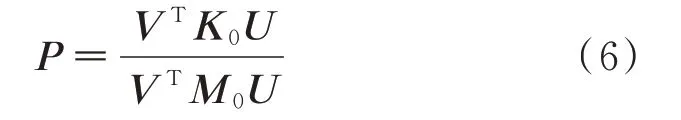
式中 特征值矩陣P為對角陣；U和V分別為式（5）的右、左特性向量矩陣。

引入復模態變量：

式中Z為廣義變量。

把式（5）代入式（6）并利用復模態理論［12，20］，式（5）變為：

式中γ為復模態振型強度系數向量，其表示為：

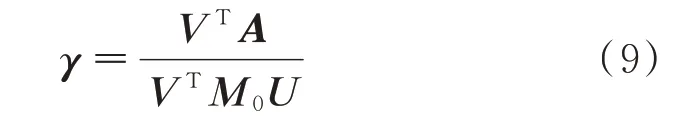
式（8）的分量形式為：

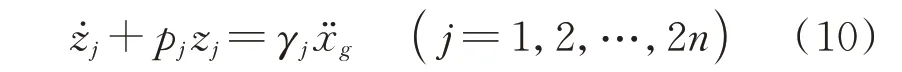
式中zj，γj和pj分別為Z，γ和P的分量。

由虛擬激勵法［15，21］，式（10）的頻域解為：

譜密度函數。

1.2 結構地震動系列響應頻域解的統一表達式

結構層相對于地面的地震動位移和層間地震動變形是工程結構抗震設計的關鍵參數；而結構層相對于地面的地震動位移變化率方差和層間地震動位移變化率方差是結構抗震動力可靠度分析的基礎。本文研究了上述地震動系列響應的統一解表達式。

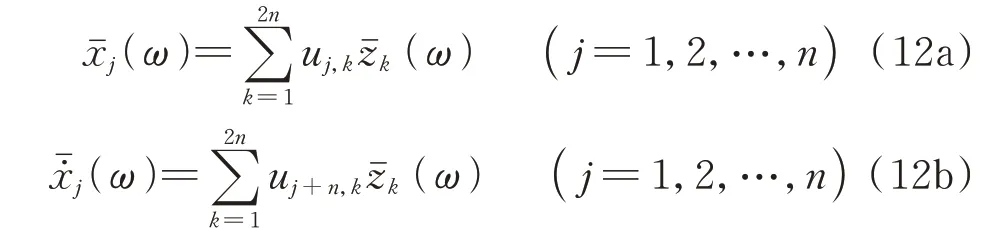
式中uj，k為右特征向量矩陣U的第j行第k列元素。

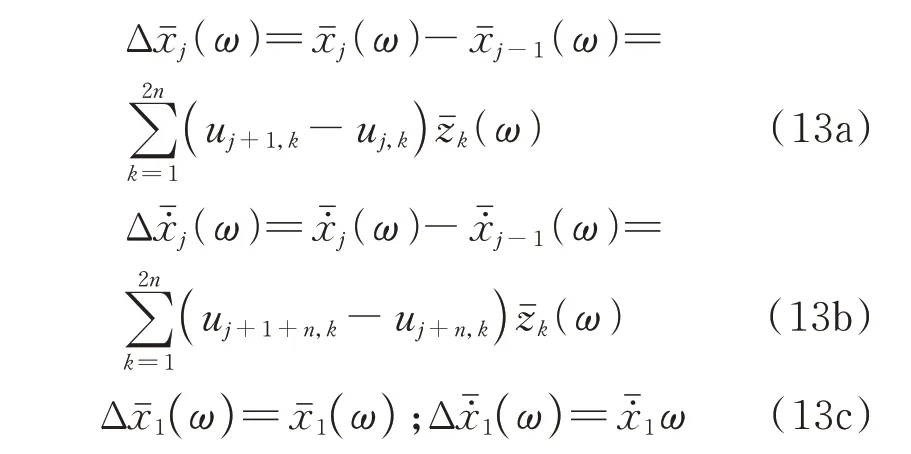
至此，結構各層位移及其變化率，層間變形及其變化率頻域解可統一表示為：

式中X(t)表示地震動響應。κk表示響應量對應的模態系數，對于結構第j層位移，κk=uj，k；對于結構第j層速度κk=uj+n，k；對于結構第j（j＞1）層層間位移，κk=uj，k-uj-1，k；對于結構第j（j＞1）層層間位移變化率，κk=uj+1+n，k-uj+n，k。

2 結構響應功率譜的二次正交化

2.1 結構頻率響應特征值函數的二次正交化

由虛擬激勵法及式（14），結構響應X的功率譜為［15，21］：

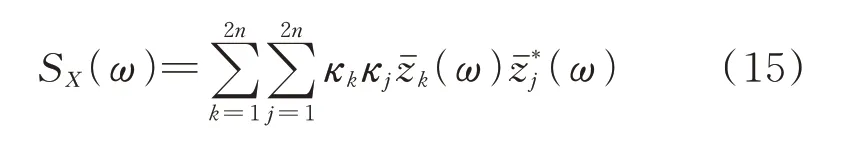
把式（11）代入式（15）：

對式（16）進行簡化：

式中

式中ηk=κkγk。

由式（18）可知，GX(ω)與地震動激勵無關，而僅與結構的振動特征值和要分析的具體響應量有關，它相當于傳遞函數法中的頻響函數模值的平方，為區別于傳統方法，稱之為結構頻率響應特征值函數。對GX(ω)做如下等價變化：

式（19）進一步簡化（簡化過程見附錄1）為：

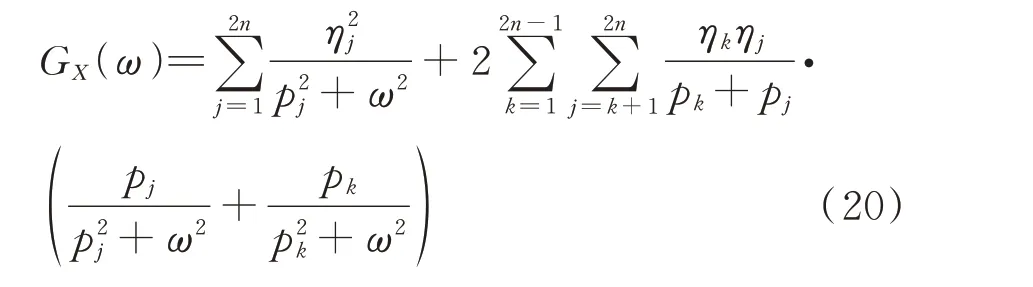
從式（20）可知，結構頻率響應特征值函數GX(ω)表示成結構體系的振動復特征值pi的平方與頻域變量ω平方和的倒數的線性組合，即結構的頻響函數HX(ω)的二次正交化。結構頻率響應特征值函數的二次正交式，表達式簡潔明了，為后文獲得結構響應0～2 階譜矩的簡明封閉解奠定基礎。

2.2 響應功率譜密度函數的二次正交化

由式（3），（17）及（20），則結構地震動響應的功率譜可表示為（具體過程見附錄2）：

式中

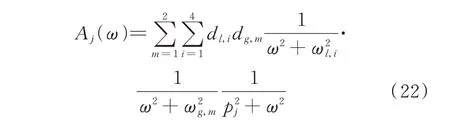
由式（21）及（22）可知，結構地震動響應功率譜密度函數轉化為地震動卓越頻率與結構頻響函數的簡明關系，為后文結構響應方差和0～2 譜矩的分析奠定了基礎。

3 響應0～2 階譜矩及方差的封閉解

由譜矩定義［12］，地震動響應的q階譜矩αX，q：

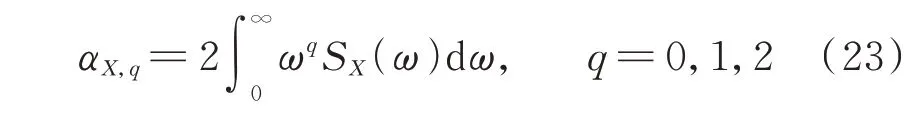
3.1 響應的0 階譜矩及1 階譜矩簡明封閉解

把式（21）代入式（23），則結構響應的譜矩為：

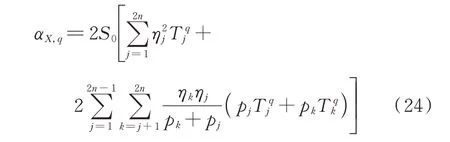
式中

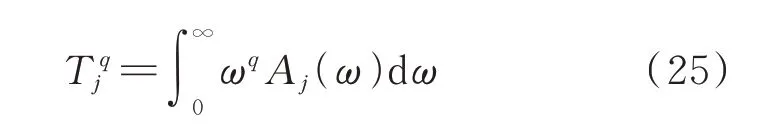
把q=0 及q=1 分別代入式（25）中，可獲得和的值（具體見附錄3）：

由式（24）和（26a）可獲得結構響應的0 階譜矩；由式（24）和（26b）可獲得結構響應的1 階譜矩。

3.2 地震動響應的2 階譜矩封閉解

由隨機振動理論［12］，平穩地震動響應變化率的0 階譜矩等于其平穩響應的2 階譜矩。因此，結構響應的2 階譜矩可由對于響應量的變化率的0 階譜矩表示：

由式（24）和（27）可知，結構響應的2 階譜矩均具有封閉解，且表達式簡潔明了。

3.3 地震動響應的方差的封閉解

由隨機振動理論［12］，結構響應方差等于其0 階譜矩，結構響應變化率的方差等于其2 階譜矩：

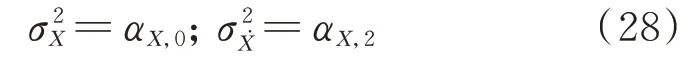
由式（24），（27）和（28）可知，本文獲得了結構位移響應及其變化率的方差。

4 數值算例

4.1 算例1

單自由度質量為1，結構的自振圓頻率ω0=5 rad/s，結構的阻尼比ξ0=0.05。李鴻晶功率譜參數為文獻［11］中表3 的廣元石井觀測站擬合值：S0=1.147 cm2/s3，ξg=0.5，ωg=9.414 rad/s，ωl=3.404 rad/s，ωh=8.955 rad/s。

傳統方法的質點位移響應功率譜Sx(ω)和速度響應功率譜分別為：

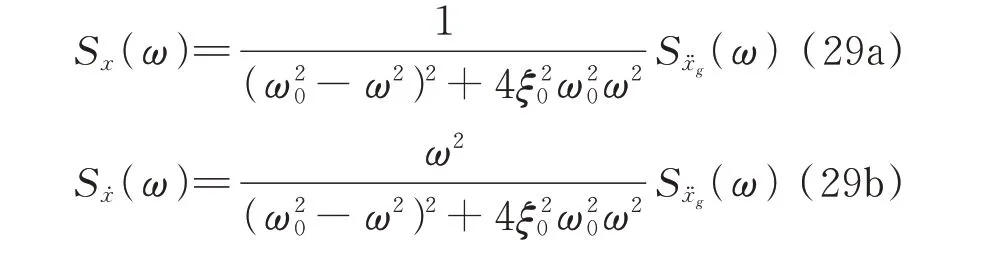
本文方法獲得的質點位移、速度響應功率譜密度函數為式（21），式中pj依據式（6）按照復模態方法獲得，κj依據式（14）獲得。其中，式（5）的參數如下：

圖1 和2 分別為傳統方法和本文方法的位移響應功率譜和速度響應功率譜的對比圖（圖上橫坐標間距為0.25 rad/s）。從圖中可知，本文方法與傳統虛擬激勵法完全一致，說明本文所獲得的李鴻晶譜等效形式、結構頻率響應特征值函數二次正交式和結構響應功率譜的二次正交式的正確性。

圖1 位移功率譜對比圖Fig.1 Comparison diagram of PSDF of displacement

圖2 速度功率譜對比圖Fig.2 Comparison diagram of PSDF of velocity

4.2 算例2

對10 層鋼筋混凝土一榀框架進行地震動響應分析，結構參數為：柱子截面取600×600 mm2，材料彈性模量E為3.0×1010N/m2，框架跨度為6 m，各層層高為4.2 m，結構阻尼比為0.05，考慮結構自重及荷載等效質量為45 t/層；按剛性樓板假定，結構層間抗側剛度k=24EI/h3，式中，I為柱截面的慣性矩，h為層高；結構的基本頻率為7.08 rad/s。頂層設置TMD 阻尼器，質量為12.4 t，抗側剛度為6.5×105N/m，阻尼比0.15，TMD的自振頻率為7.24 rad/s。李鴻晶功率譜參數與算例1 相同。

頂層設置TMD 的建筑結構可看作在頂層增加一層的結構，采用與傳統結構形式一致的運動方程，只是結構部分的阻尼采用瑞利阻尼。

4.2.1 本文方法的正確性驗證

為驗證本文所獲得的結構地震動系列響應0～2階譜矩及加速度方差的正確性，與虛擬激勵法進行對比分析。由于虛擬激勵法（PEM）分析結構響應譜矩和方差時受積分步長和積分區間的影響較大，積分區間上限暫定200 rad/s，積分步長取3 種，具體如圖3～8所示。由圖可知，隨著積分步長的減少，虛擬激勵法所得譜矩與本文方法越來越接近，說明本文方法的正確性。同時說明，虛擬激勵法在分析隨機響應譜矩時積分步長的選擇對于分析精度至關重要。

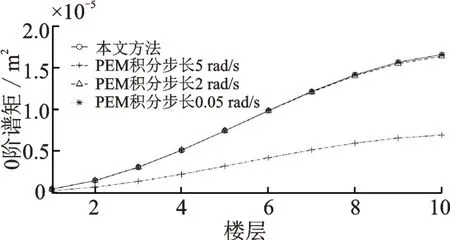
圖3 位移0 階譜矩對比圖Fig.3 Comparison diagram of 0-order spectral moment of displacement

圖4 位移1 階譜矩對比圖Fig.4 Comparison diagram of 1st order spectral moment of displacement

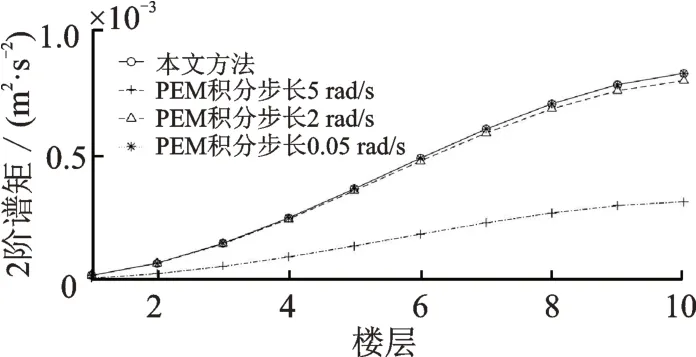
圖5 位移2 階譜矩對比圖Fig.5 Comparison diagram of 2nd order spectral moment of displacement

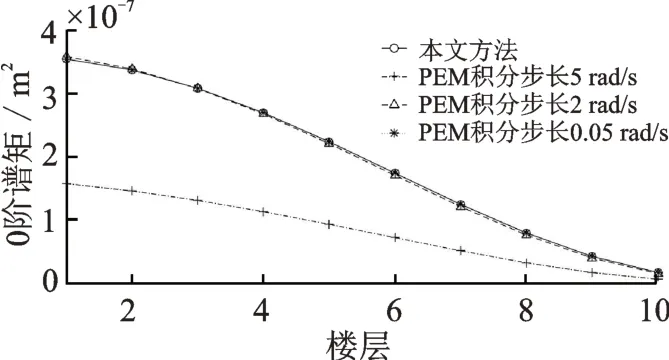
圖6 層間位移0 階譜矩對比圖Fig.6 Comparison diagram 0-order spectral moment of interlayer displacement

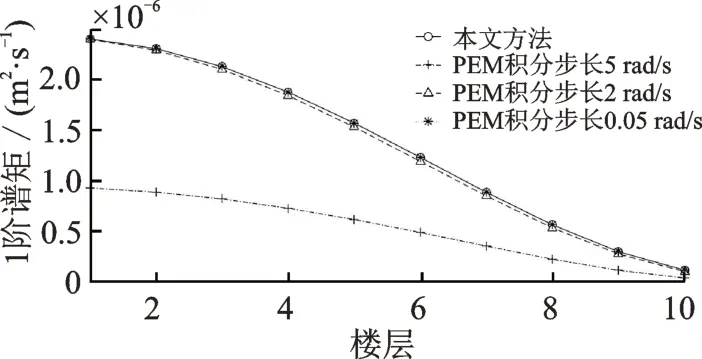
圖7 層間位移1 階譜矩對比圖Fig.7 Comparison diagram of 1st order spectral moment of interlayer displacement

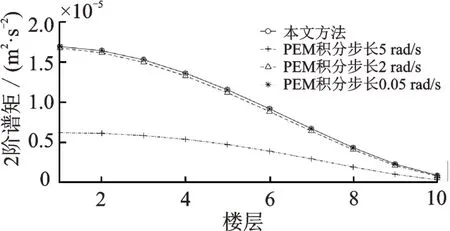
圖8 層間位移2 階譜矩對比圖Fig.8 Comparison diagram of 2nd order spectral moment of interlayer displacement

4.2.2 虛擬激勵法（PEM）積分區間對其精度的影響分析

由“4.2.1 節”可知，本文方法所獲得譜矩為封閉解，且可用來驗證虛擬激勵法的精度。而目前文獻對于虛擬激勵法的積分區間沒有明確的規定，為此，本文對其合理的積分區間進行了研究。“4.2.1 節”研究表明積分步長取0.05 rad/s 時虛擬激勵法基本與本文方法重合，為此，取積分區間上限分別為7.5，15和30 rad/s，取積分步長0.05 rad/s 進行分析，如圖9～14所示。

由圖9～14 可知，積分區間［0，7.5］rad/s 的虛擬激勵法的誤差較大；當積分區間為［0，15］rad/s 時，位移和層間位移的0 階和1 階譜矩接近精確解（本文方法），而對應的二階譜矩誤差存在一定的偏差；當積分區間為［0，30］rad/s 時，響應的0～2 階譜矩均與本文方法重合。因此，對于虛擬激勵法在分析譜矩時，需要試算積分區間才能保證計算精度。因此，本文方法可用于校核虛擬激勵法的分析精度。

圖9 PEM 分析位移0 階譜矩與積分區間關系Fig.9 Relationship between 0-order spectral moment of displacement and integrating range analyzed by PEM

圖10 PEM 分析位移1 階譜矩與積分區間關系Fig.10 Relationship between 1st order spectral moment of displacement and integrating range analyzed by PEM

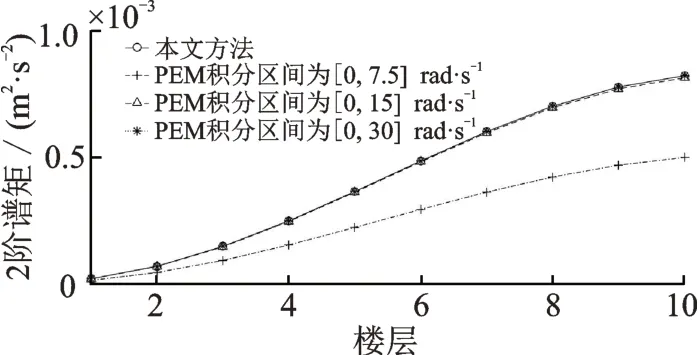
圖11 PEM 分析位移2 階譜矩與積分區間關系Fig.11 Relationship between 2nd order spectral moment of displacement and integrating range analyzed by PEM

圖12 PEM 分析層間位移0 階譜矩與積分區間關系Fig.12 Relationship between 0-order spectral moment of interlayer displacement and integrating range analyzed by PEM

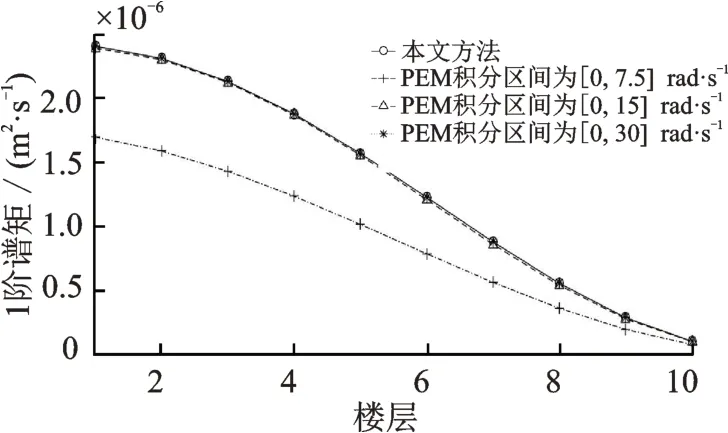
圖13 PEM 分析層間位移1 階譜矩與積分區間關系Fig.13 Relationship between 1st order spectral moment of interlayer displacement and integrating range analyzed by PEM

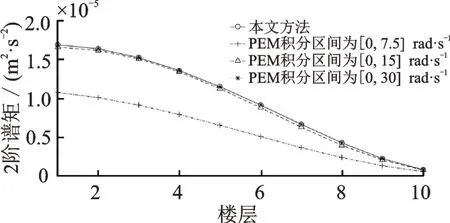
圖14 PEM 分析層間位移2 階譜矩與積分區間關系Fig.14 Relationship between 2nd order spectral moment of interlayer displacement and integrating range analyzed by PEM

5 結論

針對既有方法分析平穩激勵下線性結構隨機地震動響應方差和0～2 階譜矩頻域法無解析解或時域法解析解復雜的問題，本文提出了結構響應功率譜密度函數的二次正交化法，并成功獲得線性結構基于李鴻晶地震動功率譜的0～2 階譜矩和方差的簡明封閉解，主要結論如下：

（1）利用復模態方法對線性結構地震動方程進行解耦，將結構的地震動化為一階微分方程組的線性組合；利用一階微分方程的虛擬激勵法，獲得了結構響應的頻域解，并獲得了結構層位移和速度，結構層相對位移及其變化率的統一形式的簡明頻域解；最后給出了結構頻率響應特征值函數的二次正交式。

（2）基于留數定理給出了李鴻晶功率譜的二次正交式，本方法同樣適用于其他平穩功率譜的二次正交化。

（3）在獲得結構系列響應的頻率響應特征值函數二次正交式和地震動激勵二次正交式的基礎上，進而獲得了結構系列響應功率譜密度函數的二次正交式，為獲得結構系列響應的0～2 階譜矩和方差的簡明封閉解奠定基礎。

（4）通過一單自由度和一多自由度TMD 結構對比分析了本分方法和傳統虛擬激勵法，研究表明本文方法所獲得系列響應功率譜密度函數和0～2階譜矩的封閉解的正確性。本文方法可用來驗證虛擬激勵法積分步長和積分間距對于結構響應譜矩和方差的精度。

（5）由于本文獲得了結構動力響應的0～2 階譜矩和方差的簡明封閉解，可為結構動力可靠度分析提供新思路。

附錄1 式（19）的簡化過程

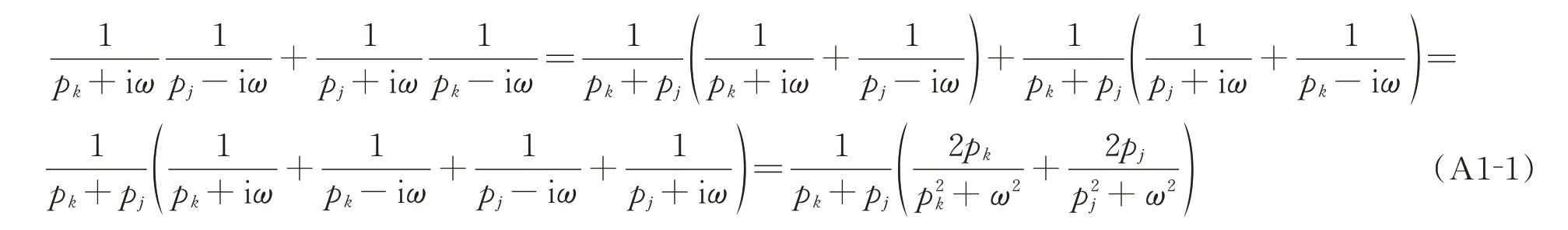
附錄2 式（21）的簡化過程

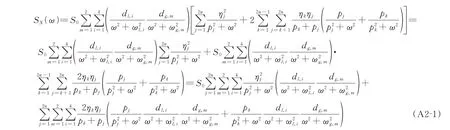
所以

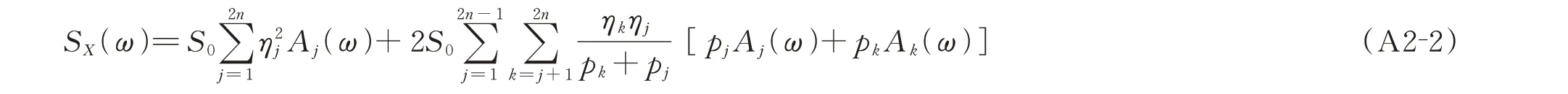
式中

附錄3和的推導