220 kV單回路干字型耐張塔繞引跳線長度計算研究
李 博,黃 國,劉勝春,尚 鑫
(1.國網內蒙古東部電力有限公司電力科學研究院,內蒙古 呼和浩特 010010;2.中國電力科學研究院有限公司,北京 102401)
近年來,途經內蒙、西北大風區的輸電線路越來越多,頻發的大風氣象條件對線路運行的安全性和可靠性提出了更高的要求,特別是內蒙、新疆、甘肅和寧夏等部分地區,輸電線路途經區域地形復雜,大風區段多且風力持續時間長,很容易造成輸電線路風害故障,文獻[1]指出線路的風偏故障發生是由于風向與導線方向垂直時的瞬時風力所導致的,風速急劇上升,對應的風向會不斷變化,一旦風向與導線方向垂直,風速超出設計值往往會引發風偏跳閘。預防和控制導線風偏的科學方法主要有改進耐張塔的跳線、優化塔型等。文獻[2]指出風偏跳閘為風害故障的主要類型,據不完全統計,國內某區域5 a內110(66) kV及以上輸電線路共發生風害故障769次,其中688次風偏跳閘故障,占風害故障總次數的89.47%。
2013年—2020年,蒙東地區220 kV及以上線路共發生47次風偏跳閘,其中220 kV共43次,占比91%,干字型耐張塔繞跳風偏13次,占比30.2%,220 kV單回路干字型耐張塔塔頭相對較小,絕緣子串相對較長,繞跳形狀較為復雜,設計時無法給出軟跳線的準確長度,只能施工時現場放樣,跳線長度常常出現冗余或不足,難以達到設計的效果,容易發生風偏故障[3-8],針對上述問題,本文在通遼搭建了220 kV單回路耐張塔塔頭-跳線真型試驗裝置,研究了不同轉角、不同高差條件下,220 kV單回路干字型耐張塔繞引跳線長度計算方法,有效指導繞跳設計及施工工作。
1 跳線長度計算
1.1 鐵木辛珂梁理論
相比于大跨度的輸電導線,繞引跳線長度較短,其抗彎剛度、扭轉剛度的影響更為明顯,因此可以采用梁單元進行模擬。本文有限元方法采用鐵木辛珂梁單元,軸向拉伸、截面彎曲和剪切變形均得到了考慮,尤其在考慮幾何非線性后有限元方法適合用于模擬大轉動且小變形問題。
梁單元用于模擬有彎曲剛度的細長結構,其抗彎剛度與截面的形狀相關,其軸向和扭轉位移場采用一維線性Lagrangian 形函數,兩個撓度方向和兩個彎曲轉角方向的位移場采用Hermite形函數,該函數滿足節點值與節點斜率的連續性要求。
梁單元采用的插值形函數為:
(1)
其中,H1和H2為Lagrangian形函數;H3~H6為Hermite形函數;l為梁單元長度;x為沿梁中和軸方向的局部坐標,需要將局部坐標系下描述的插值位移場變換為全局坐標系下。
1.2 非線性有限元迭代法
1.2.1 基本方程
采用有限單元法求解跳線在重力荷載作用下的響應,求解的基本物理場包括跳線的位移、應變和應力。跳線的運動狀態和變形情況由平衡(運動)方程、幾何方程和本構方程所確定。跳線的響應一般為非線性,不同的非線性描述會有不同的幾何和本構方程。
考慮跳線在自重、風載等工況下的力學響應,則各個微分方程可以寫為如下的形式:
平衡微分方程:
描述跳線各個物質點的力平衡狀態:
aij,j+fi=ρüi
(2)
其中,σij為應力張量的分量;σij,j為對坐標的導數(重復腳標表示求和);fi為體力分量;ρ為密度;üi為加速度分量。
幾何方程:
描述跳線的位移和變形關系:
(3)
其中,εij為工程應變張量的分量;ui為位移分量;ui,j為對初始坐標的導數。
本構方程:
描述跳線的材料屬性,即應力-應變關系:
σij=2μεij+λδijεkk
(4)
其中,μ和λ均為Lame常數;δij為Kronecker delta張量。
1.2.2 變形、應變和應力的度量
變形梯度F的定義:
(5)
dxi=FijdXj
(6)
其中,xi為現時坐標的分量;Xj為Updated Lagrangian構型中的參考坐標的分量。
變形梯度可以分解為轉動張量R和右拉伸張量U,或分解為左拉伸張量V和轉動張量R:
F=R·U=V·R
(7)
其中,矩陣R為正交矩陣;矩陣U和V為對稱矩陣。
跳線屬于大轉動小變形分析,故應變采用格林應變:
(8)
(9)
其中,▽0u為位移對初始坐標梯度;Xi為初始坐標分量;ui為位移分量;ε為應變張量;εij為應變分量。
應力采用Second Piola-Kirchhoff (PK2)應力S:
n0·SdΓ0=F-1t0dΓ0
(10)
其中,F為變形梯度;dΓ0為跳線表面上在初始時刻(變形前)的一個微面;n0為該微面在初始時刻的法向量;t0為面力。
1.3 繞引跳線長度求解
虛功原理:對于跳線結構(體積V,表面積Ω),在外力(體力fb,面力fs)和慣性力(-ρü)的作用下達到平衡,則系統發生虛位移δu時各個力所作的虛功為0。即:

(11)
其中,σ為跳線應力張。
把跳線劃分成離散的單元和節點,對應每一個單元,將位移場按照節點位移進行插值有:
(12)
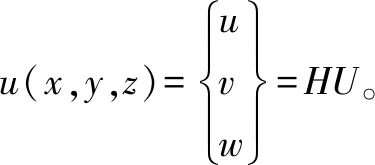
其中,H為形函數矩陣;U為節點位移向量;N為單元節點總數;u,v和w為沿三個坐標軸方向的平動位移場;ui,vi和wi為各個有限元節點的平動位移。
考慮工程應變和彈性應力應變關系,代入插值后的位移場:
(13)
(14)
其中,B為形函數對坐標的導數構成的矩陣;D為6×6 的材料彈性本構矩陣;X在此處為初始坐標矩陣。注意應變ε和應力σ在式(13),式(14)中為含有6個分量的向量形式,而在式(11)為張量形式。
式(11)中的V和Ω可以考慮為V0和Ω0,分別表示跳線初始構型的體積和表面積,將式(13),式(14)代入虛功原理式(11):

(15)
兩邊消去虛位移δU得:
Mü+KU=Fex
(16)
(17)
(18)
(19)
方程(16)即為一個單元的有限元平衡方程,其中M為單元質量矩陣;K為單元剛度矩陣;Fex為單元等效節點荷載向量。
將單元質量矩陣、單元剛度矩陣和單元等效節點荷載向量組裝成總質量矩陣、總剛度矩陣和總荷載列向量,可得:
MGüG+KGUG=FexG
(20)
方程(20)即為總的有限元離散方程,可以使用牛頓迭代法求解。
采用牛頓迭代法對方程(20)進行求解,可以得到跳線各點的位移U和空間坐標X,設跳線某一單元的長度為ds,則有:
ds=αdζ
(21)
其中:
(22)
(23)
其中,hζi為跳線形函數的導數。
跳線某一單元的長度li為:
(24)
跳線整體進行積分求和,得到跳線長度為:
(25)
2 繞引跳線算法優化
在蒙東電科院通遼試驗基地搭建220 kV單回路干字型耐張塔塔頭-跳線試驗裝置,現場布置如圖1所示。
中間為220 kV單回路干字型耐張塔塔頭,左右兩端為荷載支架,每個支架分為上下兩層,用于模擬不同高差,每層下端均有不同位置導線掛點,用于模擬不同轉角,上層導線掛點高于塔頭導線掛點,下層導線掛點與塔頭導線掛點持平,支架兩端各有一臺卷揚機,用于收放導線,需要說明的,跳線兩端并沒有進行壓接,而是通過特制的U型螺絲固定,以便于在不同工況下,調節條件跳線的長度,試驗時,利用全站儀進行三維坐標測量,測量點為:a支架端三角聯板、b耐張線夾、c耐張串兩端三角聯板、d懸垂線夾、e懸垂串上掛點,如圖2所示。

利用真型試驗鐵塔計算不同轉角、不同高差的實際跳線長度,本次共計測量了21組不同轉角、不同高差下的跳線長度,計算結果如表1所示。
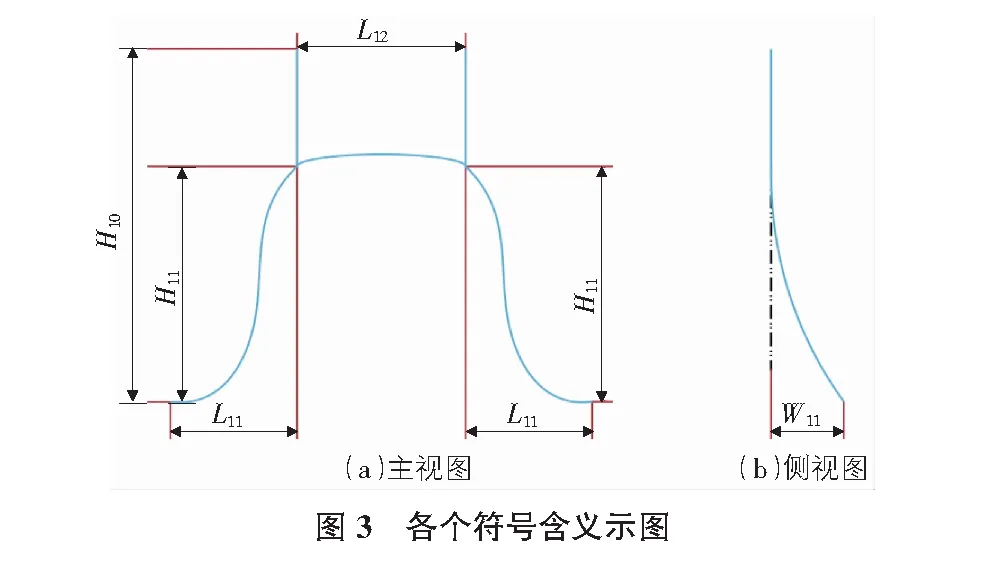
其中各個量含義如圖3所示。
圖3中L11為耐張線夾與懸垂線夾水平距離;L12為懸垂線夾水平間距;H11為耐張線夾與懸垂線夾垂直間距;H10為懸垂串掛點與耐張線夾垂直間距;W11為懸垂線夾與耐張線夾側向間距。
表中“上”的含義為兩側支架的上層掛點,“下”的含義為兩側支架的下層掛點。
算法優化前,初始線長取值L0:
(26)
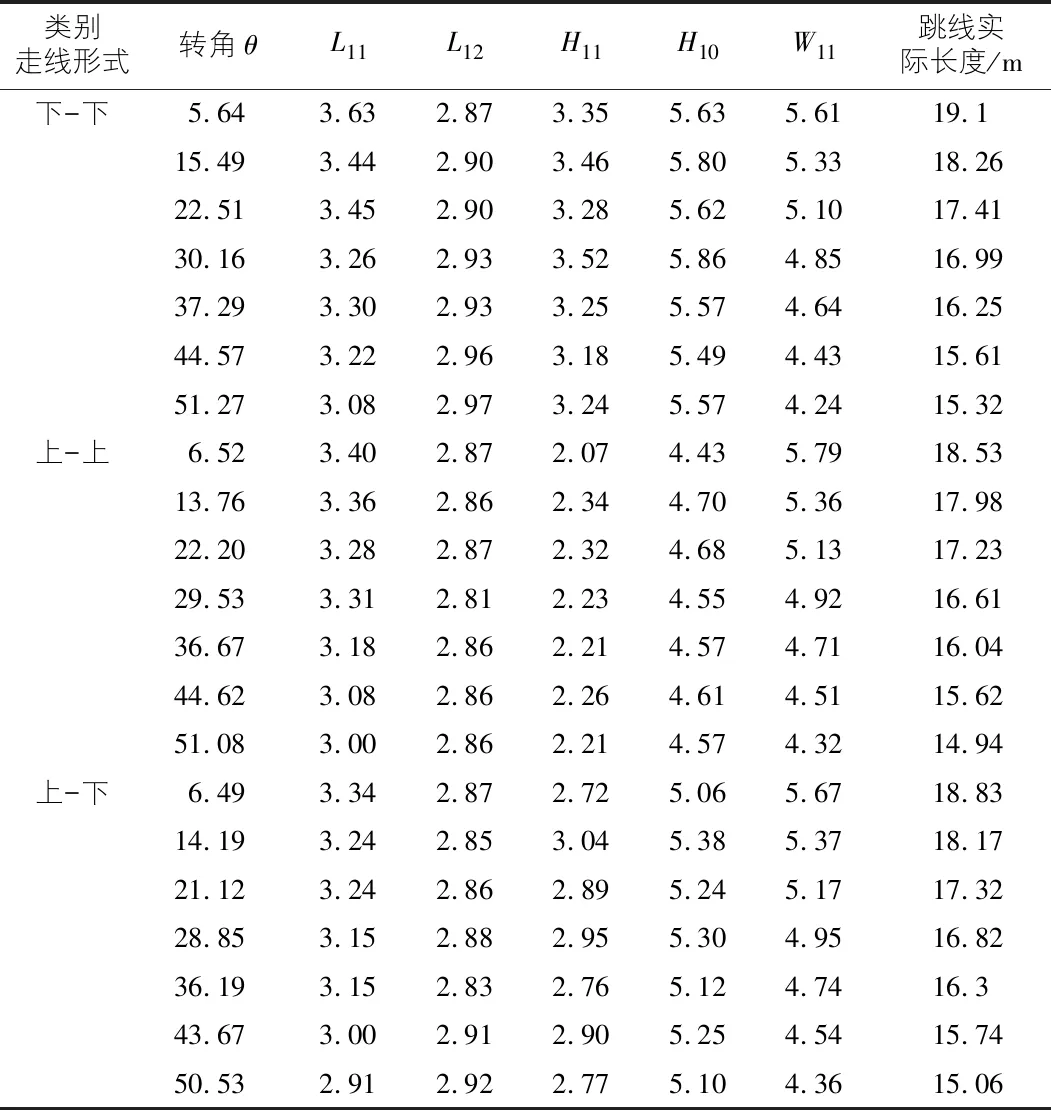
表1 測量結果
計算結果與實際值比較如表2所示。

表2 算法優化前計算結果與實際值比較表
由表2中的21組數據可以看出,計算得到的繞跳長度與實際值相比誤差基本都在2%以上,最大達到-4.12%,與實際值相差64 cm,誤差較大。
對比現場測量數據,采用非線性擬合法對初始值L0修正,引入初始值修正系數y:
(27)
則算法優化后初始線長取值L:
L=y×L0
(28)
算法優化后計算結果與實際值比較如表3所示。
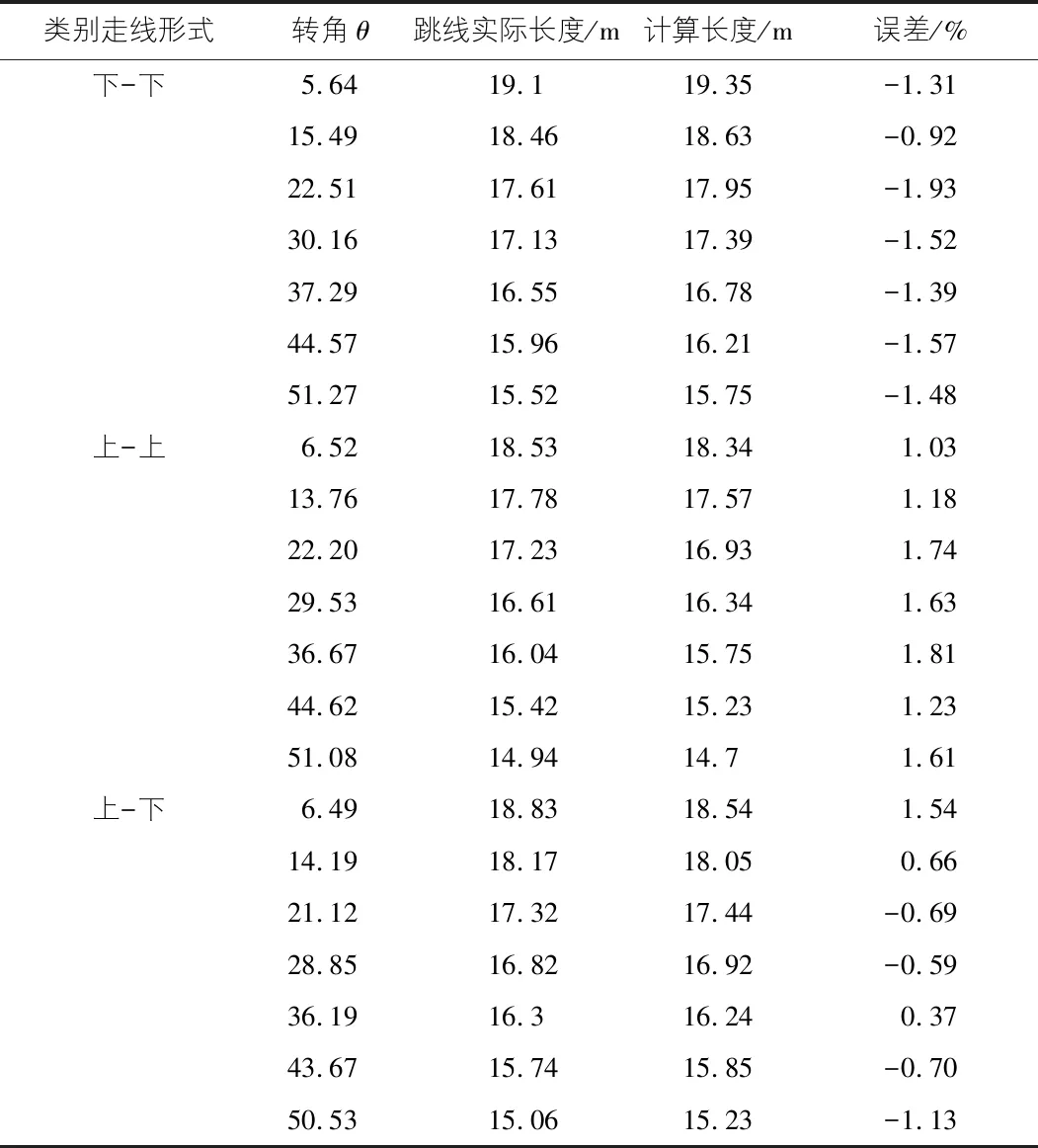
表3 算法優化后計算結果與實際值比較表
由表3可以看出,優化后的算法誤差在2%以內,對比表2和表3可以發現,相比于優化前,優化后計算誤差明顯降低,最大降低了2.64%,彌補了理論計算上的不足,使得計算結果更加接近實際值。
3 結語
本文利用“鐵木辛珂梁理論+非線性有限元迭代法”編制了220 kV單回路干字型耐張塔繞引跳線計算程序,并在通遼搭建了220 kV單回路耐張塔塔頭-跳線真型試驗裝置,通過開展21個不同轉角、不同高差試驗,得到相應的21組不同工況下實際繞引跳線長度,進而完善繞引跳線計算方法,使得計算誤差在±2%以內,形成完整的220 kV單回路干字型耐張塔繞引跳線長度計算系統,有效指導繞引跳線設計及施工工作,從根本上降低繞引跳線風偏故障。