用于變體飛行器的波紋板等效強(qiáng)度模型及其優(yōu)化設(shè)計(jì)

王晨，楊洋，沈星,*，夏育穎

1. 南京航空航天大學(xué) 機(jī)械結(jié)構(gòu)力學(xué)及控制國(guó)家重點(diǎn)實(shí)驗(yàn)室，南京 210016 2. 斯旺西大學(xué) 工程學(xué)院，斯望西 SA1 8EN

變體飛行器可以根據(jù)飛行條件的變化，自適應(yīng)地改變自身氣動(dòng)外形，從而提高飛行器性能。歐盟MorphLET項(xiàng)目的研究表明，在不同的飛行階段，通過(guò)機(jī)翼翼尖的彎折變形，可以在不同飛行階段保持最優(yōu)的升阻比，從而提高飛機(jī)航程。通過(guò)機(jī)翼外段的不對(duì)稱折疊變形，還可以產(chǎn)生滾轉(zhuǎn)力矩，起到控制飛機(jī)飛行的作用。此外，在面臨陣風(fēng)載荷的影響時(shí)，如果允許機(jī)翼翼尖發(fā)生彎折變形，可以降低機(jī)翼翼根部的載荷，起到載荷減緩的作用。

變體翼尖發(fā)生彎折變形，屬于機(jī)翼面外變形，且其投影方向?yàn)闄C(jī)翼展向，需要克服展向氣動(dòng)載荷的作用。同時(shí)，機(jī)翼翼尖處的厚度較低，可以用于布置結(jié)構(gòu)與驅(qū)動(dòng)的空間較小，這些都對(duì)變體翼尖的結(jié)構(gòu)設(shè)計(jì)提出了較高要求。

歐盟MorphLET項(xiàng)目中，使用波紋板用于連接機(jī)翼與變形翼尖的結(jié)構(gòu)設(shè)計(jì)。波紋板結(jié)構(gòu)具有高度各向異性的特征，常常作為變體飛行器結(jié)構(gòu)的備選方案之一進(jìn)行研究。

針對(duì)圖1所示的變體翼尖設(shè)計(jì)，使用波紋板用于連接機(jī)翼與變體翼尖的固定外形段，實(shí)現(xiàn)在不同的飛行階段改變翼尖折疊角度。由于波紋板結(jié)構(gòu)沿著波紋方向剛度較低，在受壓時(shí)容易發(fā)生失穩(wěn)變形。通過(guò)在變體翼尖結(jié)構(gòu)中引入非對(duì)稱剛度，可以使變體結(jié)構(gòu)上下表面的波紋板發(fā)生非對(duì)稱伸長(zhǎng)，從而實(shí)現(xiàn)變體翼尖彎折變形，并且避免波紋板受壓失穩(wěn)。波紋板與彈性體蒙皮組成復(fù)合結(jié)構(gòu)，在滿足氣動(dòng)表面設(shè)計(jì)要求的同時(shí)，由波紋板提供足夠的支撐。因此，在該變體翼尖中，波紋板結(jié)構(gòu)既需要能夠發(fā)生足夠的拉伸變形以實(shí)現(xiàn)翼尖彎折變形，也需要具有一定的彎曲剛度，以傳遞載荷。然而，目前對(duì)波紋板力學(xué)問(wèn)題的研究中，較多的側(cè)重于對(duì)其剛度特性的預(yù)測(cè)和屈曲特性的研究，對(duì)其強(qiáng)度特性的研究仍然較少；尤其是缺少對(duì)波紋板結(jié)構(gòu)等效強(qiáng)度模型的研究，在變體飛行器概念設(shè)計(jì)階段，難以對(duì)波紋板結(jié)構(gòu)的失效應(yīng)變進(jìn)行快速預(yù)測(cè)，制約了變體飛行器的發(fā)展。

圖1 變體翼尖設(shè)計(jì)概念與波紋板結(jié)構(gòu)布置示意圖Fig.1 Conceptual design of morphing wingtip and layout of corrugated panels

針對(duì)這一需求，本文將研究一種波紋板等效力學(xué)模型，并面向變體翼尖的應(yīng)用場(chǎng)景開(kāi)展優(yōu)化設(shè)計(jì)。首先，將對(duì)等效力學(xué)模型進(jìn)行推導(dǎo)，并對(duì)結(jié)果進(jìn)行實(shí)驗(yàn)驗(yàn)證。該模型可以通過(guò)轉(zhuǎn)換矩陣將波紋板全局應(yīng)變轉(zhuǎn)換為結(jié)構(gòu)材料的局部應(yīng)變，從而為預(yù)測(cè)波紋板結(jié)構(gòu)整體的失效應(yīng)變提供依據(jù)；然后根據(jù)該等效力學(xué)模型，對(duì)波紋板結(jié)構(gòu)的強(qiáng)度和剛度特性進(jìn)行幾何參數(shù)分析；最后，面向變體翼尖的使用需求，對(duì)波紋板結(jié)構(gòu)進(jìn)行優(yōu)化設(shè)計(jì)。

1 波紋板等效力學(xué)模型

1.1 基于代表單元的等效力學(xué)模型

波紋板結(jié)構(gòu)是一種周期性結(jié)構(gòu)，可以描述為具有重復(fù)形狀的板結(jié)構(gòu)，如圖2所示。波紋板等效力學(xué)模型可以通過(guò)單個(gè)波紋板單元的幾何尺寸和材料屬性實(shí)現(xiàn)對(duì)波紋板整體力學(xué)特性的預(yù)測(cè)，從而將具有復(fù)雜外形的波紋板結(jié)構(gòu)等效為各向異性板進(jìn)行處理。不失一般性，本文中選擇圓形和梯形波紋板單元作為示例，如圖2所示。坐標(biāo)系“”為全局坐標(biāo)系，用于描述波紋板整體的等效變形。坐標(biāo)系“”為波紋板單元的局部坐標(biāo)系，其中坐標(biāo)軸為波紋板單元切向，坐標(biāo)軸為法向，坐標(biāo)軸為波紋板結(jié)構(gòu)寬度方向。局部坐標(biāo)系用于定義波紋板單元的幾何形狀，并實(shí)現(xiàn)不同載荷工況情況下的代表單元受力分析。波紋板的寬度使用變量表示，圓形代表單元的幾何參數(shù)包括半徑和長(zhǎng)度；梯形代表單元的幾何參數(shù)包括梯形長(zhǎng)度、及傾斜角。與此同時(shí)，為了方便公式推導(dǎo)，圓形與梯形單元沿軸的長(zhǎng)度均使用2表示。

圖2 波紋板結(jié)構(gòu)整體及圓形梯形代表單元示意圖Fig.2 Sketch of corrugated panels with round and trapezoidal corrugation units

本文研究的等效模型主要用于變體飛行器概念設(shè)計(jì)階段的波紋板結(jié)構(gòu)分析與優(yōu)化設(shè)計(jì)，波紋板結(jié)構(gòu)材料發(fā)生的變形以小尺度變形為主；同時(shí)，波紋板結(jié)構(gòu)材料在局部坐標(biāo)系下滿足經(jīng)典板理論的要求。

波紋板的等效力學(xué)模型分為等效剛度模型和等效強(qiáng)度模型2類。在全局坐標(biāo)系下，波紋板的整體力學(xué)特性為

(1)

在局部坐標(biāo)系下，波紋板結(jié)構(gòu)的內(nèi)力應(yīng)變關(guān)系可以由一般的經(jīng)典板理論表示為

(2)

(3)

式(3)左側(cè)為波紋板中性面上的局部應(yīng)變，右側(cè)為波紋板整體等效應(yīng)變值。使用式(3)，可以根據(jù)波紋板發(fā)生變形時(shí)的整體應(yīng)變值，推測(cè)出波紋板材料局部的應(yīng)變值，從而獲得波紋板結(jié)構(gòu)的局部應(yīng)變分布。在此基礎(chǔ)上，結(jié)合波紋板結(jié)構(gòu)材料的失效準(zhǔn)則，實(shí)現(xiàn)對(duì)波紋板整體強(qiáng)度特性的評(píng)估。

對(duì)波紋板結(jié)構(gòu)的代表單元進(jìn)行分析，假定波紋板結(jié)構(gòu)符合經(jīng)典板理論，對(duì)波紋板單元逐次施加如表1所示的邊界條件。

表1 波紋板單元邊界條件Table 1 Boundary conditions of corrugation unit

以邊界條件為[1，0，0，0，0，0]為例，根據(jù)式(1) 可知：

(4)

根據(jù)對(duì)稱性，推測(cè)其局部應(yīng)變應(yīng)滿足====0，考慮到全局應(yīng)變只發(fā)生在方向，則全局內(nèi)力和局部?jī)?nèi)力存在平衡關(guān)系：

(5)

由于方向的應(yīng)變?yōu)?，因此根據(jù)波紋局部坐標(biāo)系下的內(nèi)力應(yīng)變關(guān)系，得到

(6)

同樣，比較全局與局部坐標(biāo)系下的力矩項(xiàng)，并且根據(jù)局部曲率變化為0，可以得到

(7)

對(duì)波紋板單元使用能量法計(jì)算其應(yīng)變能，并進(jìn)行公式整理可以得到

(8)

對(duì)等效的各向異性板，同樣使用能量法可以得到

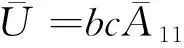
(9)

(10)

同時(shí)，由力學(xué)平衡可以得到

(11)

因此，根據(jù)邊界條件：

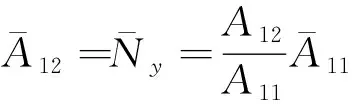
(12)

在表1的其他邊界條件下，使用類似的方法進(jìn)行推導(dǎo)，可以獲得式(1)中等效剛度矩陣中的系數(shù)為

(13)

式中：為波紋板代表單元沿軸的長(zhǎng)度的一半；為沿軸長(zhǎng)度的一半。

同樣的，針對(duì)式(3)的應(yīng)變轉(zhuǎn)換矩陣，對(duì)等效各向異性板施加如表1所示的邊界條件。以邊界條件[1，0，0，0，0，0]為例，根據(jù)式(2)、式(5)和式(7)，結(jié)合局部應(yīng)變的條件，可知：

(14)

因此，根據(jù)式(3)的書(shū)寫(xiě)方式可得

(15)

在其他邊界下進(jìn)行推導(dǎo)可以得到完整的應(yīng)變轉(zhuǎn)換矩陣的表達(dá)式為

(16)

1.2 模型實(shí)驗(yàn)驗(yàn)證

在作者前期工作中，使用有限元方法對(duì)表1中的應(yīng)變轉(zhuǎn)換矩陣進(jìn)行了數(shù)值驗(yàn)證。同時(shí)，根據(jù)式(1)～式(16)的推導(dǎo)過(guò)程可知，波紋板等效剛度模型和強(qiáng)度模型均基于代表性單元在不同邊界條件下的變形假設(shè)獲得。對(duì)波紋板結(jié)構(gòu)的等效剛度進(jìn)行實(shí)驗(yàn)驗(yàn)證，可以起到對(duì)等效強(qiáng)度模型進(jìn)行間接驗(yàn)證的作用。

不失一般性，通過(guò)比較波紋板結(jié)構(gòu)沿軸拉伸模量的解析解和實(shí)驗(yàn)值，對(duì)波紋板等效力學(xué)模型進(jìn)行驗(yàn)證。實(shí)驗(yàn)樣件采用Objet 260 3D打印制作,材料為ABS塑料，材料楊氏模量標(biāo)稱為3 GPa。由于實(shí)際加工時(shí)，3D打印樣件的材料屬性受到環(huán)境溫度、濕度、材料存儲(chǔ)情況等因素的影響，實(shí)際制作的樣件的材料屬性與標(biāo)稱值相比會(huì)有所不同。因此實(shí)驗(yàn)時(shí)，在同一個(gè)批次中制備6個(gè)不同幾何參數(shù)的梯形波紋板結(jié)構(gòu)樣件，如圖3所示。6個(gè)樣件分別命名為樣件1、2、3、4、5、6。

圖3 梯形波紋板結(jié)構(gòu)實(shí)驗(yàn)樣件Fig.3 Test samples of trapezoidal corrugated panels

使用Zwick?拉伸機(jī)對(duì)樣件進(jìn)行拉伸實(shí)驗(yàn)，獲得樣件的“力-位移”曲線，波紋板拉伸實(shí)驗(yàn)實(shí)物圖如圖4所示。拉伸機(jī)最大測(cè)量范圍為2 500 N；為了避免打滑，對(duì)樣件根部進(jìn)行了加厚處理。

圖4 波紋板拉伸實(shí)驗(yàn)實(shí)物圖Fig.4 Tensile tests of corrugated panels

根據(jù)等效剛度模型，等效拉伸模量將隨著梯形夾角的增加而不斷下降。在與實(shí)驗(yàn)值比較時(shí)，為了避免材料本身?xiàng)钍夏Ａ孔兓挠绊懀瑢?shí)驗(yàn)值和解析解均根據(jù)樣件1的對(duì)應(yīng)數(shù)值進(jìn)行了歸一化處理，最終結(jié)果如圖5所示。歸一化處理后，解析解與實(shí)驗(yàn)值的變化趨勢(shì)保持一致，樣件解析解與實(shí)驗(yàn)值的平均誤差在10%以內(nèi)。因此，本文使用的波紋板等效力學(xué)模型可以用于變體翼尖在概念設(shè)計(jì)階段的優(yōu)化分析。

圖5 實(shí)驗(yàn)值和解析解對(duì)比Fig.5 Comparisons of test and analytical results

2 波紋板結(jié)構(gòu)性能參數(shù)分析

2.1 波紋板結(jié)構(gòu)拉伸失效應(yīng)變計(jì)算

使用文中等效力學(xué)模型可以獲得波紋板結(jié)構(gòu)的局部應(yīng)變與等效應(yīng)變之間的關(guān)系，如式(3)所示。其中，局部應(yīng)變?yōu)椴y板中性面的應(yīng)變值。根據(jù)經(jīng)典板理論，可以進(jìn)一步獲得波紋板沿著板厚度方向的應(yīng)變分布。以(,)表示波紋板局部坐標(biāo)“”下的波紋板坐標(biāo)。

以波紋板沿著方向發(fā)生拉伸變形為例，此時(shí)，波紋板結(jié)構(gòu)的局部應(yīng)變可以寫(xiě)為

(17)

獲得波紋板局部應(yīng)變后，可以進(jìn)一步根據(jù)波紋板結(jié)構(gòu)自身的本構(gòu)關(guān)系獲得局部應(yīng)力。

(18)

該系數(shù)可以對(duì)波紋板結(jié)構(gòu)的變形能力進(jìn)行評(píng)估。以圓形波紋板為例，對(duì)波紋板幾何形狀變化時(shí)的失效應(yīng)變和變形放大系數(shù)進(jìn)行了參數(shù)分析。波紋板結(jié)構(gòu)使用復(fù)合材料制備，鋪層角度為[0/45/-45/90]，其中0°沿著軸方向。單層厚度=0.1 mm，單層板的材料屬性如表2所示。同時(shí)，波紋板沿方向?qū)挾葹?5 mm。

圖6為圓形波紋板沿軸發(fā)生拉伸變形時(shí)的失效應(yīng)變與幾何參數(shù)之間的關(guān)系。由計(jì)算結(jié)果可知，在材料屬性和鋪層方式不變時(shí)，增加波紋板代表單元的幾何尺寸(和)，可以提高波紋板結(jié)構(gòu)的失效應(yīng)變。

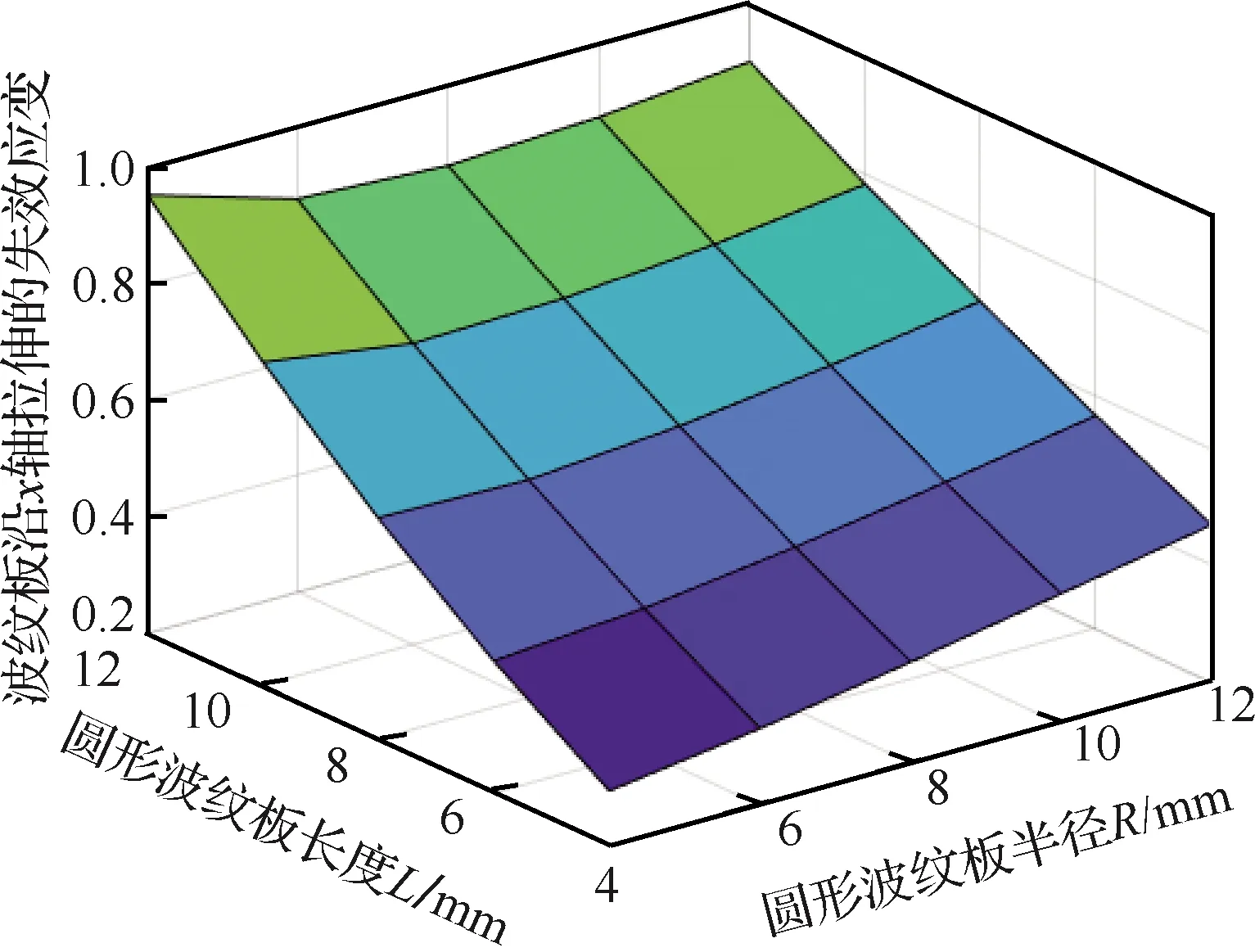
圖6 波紋板拉伸失效應(yīng)變與波紋板幾何參數(shù)的關(guān)系Fig.6 Relationship between failure strain and geometric parameters of corrugated panel

圖7更直觀地說(shuō)明了波紋板幾何參數(shù)對(duì)其結(jié)構(gòu)材料失效應(yīng)變的放大作用。相比于沒(méi)有波紋的平板，波紋板結(jié)構(gòu)可以將結(jié)構(gòu)沿軸拉伸時(shí)的失效應(yīng)變放大1～2個(gè)數(shù)量級(jí)。

圖7 波紋板拉伸變形放大系數(shù)與波紋板幾何參數(shù)的關(guān)系Fig.7 Relationship between deformation amplification coefficient and geometric parameters of corrugated panel

表2 波紋板結(jié)構(gòu)單層材料屬性Table 2 Material properties of composite lamina of the corrugated panel

圖8 波紋板拉伸失效應(yīng)變與波紋板厚度的關(guān)系Fig.8 Variation of failure strain of corrugated panel when thickness changes

2.2 波紋板結(jié)構(gòu)彎曲剛度計(jì)算

圖10進(jìn)一步計(jì)算了波紋板結(jié)構(gòu)的歸一化彎曲剛度：

(19)

從圖10中可知，歸一化彎曲剛度的變化趨勢(shì)與圖9中的彎曲剛度絕對(duì)值保持一致。同時(shí)，歸一化剛度均小于1，說(shuō)明波紋板的幾何形狀客觀上降低了其承受彎曲載荷的能力。

圖9 波紋板彎曲剛度與波紋板幾何參數(shù)的關(guān)系Fig.9 Relationship between bending stiffness and geometric parameters of corrugated panel

圖10 波紋板歸一化彎曲剛度與波紋板幾何參數(shù)的關(guān)系Fig.10 Relationship between normalized bending stiffness and geometric parameters of corrugated panel

進(jìn)一步對(duì)波紋板厚度變化時(shí)的彎曲剛度變化進(jìn)行了計(jì)算。保持波紋板幾何尺寸==4 mm，鋪層方式不變，通過(guò)改變復(fù)材鋪層厚度以改變波紋板的總體厚度，結(jié)果如圖11所示。可以發(fā)現(xiàn)，在鋪層順序和角度不變的情況下，波紋板彎曲剛度絕對(duì)值隨著厚度的增加而增加；但是由于波紋板局部剛度也隨著厚度增加而增加，其歸一化剛度保持不變。

圖11 波紋板彎曲剛度隨厚度變化Fig.11 Variation of bending stiffness of corrugated panel when thickness changes

3 波紋板結(jié)構(gòu)性能優(yōu)化

3.1 波紋板結(jié)構(gòu)性能單目標(biāo)優(yōu)化

根據(jù)第2節(jié)的計(jì)算結(jié)果可知，波紋板沿軸拉伸的失效應(yīng)變和彎曲剛度存在互斥關(guān)系。因此，在變體翼尖的設(shè)計(jì)中，需要進(jìn)行優(yōu)化設(shè)計(jì)。在優(yōu)化過(guò)程中，波紋板材料屬性，復(fù)合材料鋪層順序與角度和波紋板寬度保持不變，與第2節(jié)中一致。

優(yōu)化變量為圓形波紋板的幾何參數(shù)：

(20)

以等效彎曲剛度為優(yōu)化目標(biāo)：

(21)

考慮圖1中的設(shè)計(jì)，根據(jù)變體翼尖彎折角度的要求和前期估算，約束條件為波紋板失效應(yīng)變≥0.2，即

(22)

優(yōu)化算法使用遺傳算法，種群大小為50，優(yōu)化代數(shù)為200代，優(yōu)化結(jié)果如表3所示。從優(yōu)化結(jié)果可知，變量接近其下邊界，變量、接近其上邊界。由2.1節(jié)知，該參數(shù)變化有利于提高彎曲剛度。同時(shí)，較大的半徑有助于提高失效應(yīng)變，使波紋板滿足約束條件。因此，優(yōu)化結(jié)果符合波紋板結(jié)構(gòu)的性能規(guī)律。

表3 單目標(biāo)優(yōu)化結(jié)果Table 3 Optimized results of single objective

3.2 波紋板結(jié)構(gòu)性能多目標(biāo)優(yōu)化

在此基礎(chǔ)上，針對(duì)變體飛行器結(jié)構(gòu)承載與變形的雙重要求，進(jìn)一步開(kāi)展了多目標(biāo)優(yōu)化。優(yōu)化變量范圍見(jiàn)式(20)。優(yōu)化目標(biāo)為

(23)

采用多目標(biāo)遺傳算法進(jìn)行優(yōu)化，種群大小保持50，優(yōu)化代數(shù)設(shè)置為200代。優(yōu)化后獲得如圖12 所示的帕累托前沿和對(duì)應(yīng)的最優(yōu)解集。從圖中可知，較小的彎曲剛度對(duì)應(yīng)著較大的失效應(yīng)變，而較大的彎曲剛度則對(duì)應(yīng)著較小的失效應(yīng)變。考慮到變體飛行器需要同時(shí)滿足變形與承載的要求，該計(jì)算結(jié)果一方面從側(cè)面驗(yàn)證了使用該等效模型進(jìn)行計(jì)算的可行性，另一方面也說(shuō)明在波紋板結(jié)構(gòu)的實(shí)際使用中需要考慮具體的任務(wù)要求，確定合適的失效應(yīng)變和彎曲剛度作為設(shè)計(jì)邊界，以避免最終的波紋板結(jié)構(gòu)無(wú)法同時(shí)滿足失效應(yīng)變與彎曲剛度的要求。

圖12 波紋板結(jié)構(gòu)多目標(biāo)優(yōu)化帕累托前沿Fig.12 Pareto front of optimized corrugated panels

4 結(jié) 論

本文針對(duì)變體飛行器變形與承載的設(shè)計(jì)需要，建立了波紋板結(jié)構(gòu)的等效力學(xué)模型，開(kāi)展了初步的實(shí)驗(yàn)驗(yàn)證，并進(jìn)行了參數(shù)分析和優(yōu)化設(shè)計(jì)，主要結(jié)論如下：

1) 建立了波紋板等效力學(xué)模型，可以同時(shí)預(yù)測(cè)波紋板等效剛度和失效應(yīng)變。

2) 波紋形狀的存在，可以起到放大波紋板結(jié)構(gòu)沿軸拉伸失效應(yīng)變的作用，并可以通過(guò)等效模型推測(cè)出變形放大系數(shù)。

3) 增加波紋板厚度會(huì)降低波紋板結(jié)構(gòu)失效應(yīng)變，但是可以起到增加等效剛度的作用。

4) 針對(duì)變體飛行器承載和變形的雙重要求，需要結(jié)合具體的設(shè)計(jì)指標(biāo)，對(duì)波紋板結(jié)構(gòu)進(jìn)行優(yōu)化設(shè)計(jì)。

在未來(lái)工作中，將進(jìn)一步對(duì)強(qiáng)度模型進(jìn)行實(shí)驗(yàn)驗(yàn)證，同時(shí)針對(duì)復(fù)合材料的脫膠、分層等問(wèn)題進(jìn)行專門(mén)研究，從而拓展該模型的應(yīng)用范圍。