數據集壓縮建模的研究*

王赫楠 孫艷秋 張柯欣

（遼寧中醫藥大學信息工程學院 沈陽 110847）

1 引言

在統計學研究中，數據序列數據挖掘是研究的重點之一［1～3］。它的研究對象是事物在不同時刻變化情況所形成的數據值。目前，各行業都存在海量的數據集。比如：醫療、金融、農業等行業。通過對數據序列變化趨勢的分析和預測，揭示事物的內在規律和關聯，是當下數據集處理問題的主要方向。數據集的處理研究主要有以下幾個方面：數據序列的擬合［4～6］、數據序列的劃分［7～8］、數據序列的分類聚類［9～11］、數據序列的應用研究［12～14］、數據序列的可視化研究。

數據集的壓縮以及奇異值點的識別是數據序列數據挖掘的研究重點。做好數據集的處理，是后續進行數據分析和預測的根基。本文在分析了典型數據集處理模型的前提下，提出了數據集壓縮模型以及奇異值識別模型。數據集壓縮模型使用了自定義函數，符合數據集的時間局部性原理，考慮了數據集的時間特性，并且支持實時數據的處理問題。奇異值識別模型在原有模型的基礎上，對于一些關鍵奇異值數據的識別更具優勢。

2 數據集壓縮模型

數據集壓縮是對數據結構進行優化的一種非常重要的手段。幾年來，經過計算機、數學等各方面研究人員的不斷探索，提出了很多消除數據冗余的方法，在數據處理、數據壓縮等方面取得了非常大的進步。

原始數據集存放在一個n 維的向量中，數據集的數據量過大及維數過高，會對后期數據的整理及分析造成干擾。我們需要對數據進行壓縮處理，既能用更少的數據來索引原始數據集，又能很好地反映原始數據集的趨勢變化，從而挖掘出研究者需要的有價值的信息。本文在分析了兩種典型的數據集壓縮方法的前提下，提出了一種新的數據集壓縮模型。

2.1 壓縮模型（一）

壓縮模型（一）將原始數據集劃分成若干段，在限制分段誤差的前提下，利用各段的均值來索引原始數據集，以此達到降維的目的。

這種方法作為數據降維的一種常用手段，非常的簡單。我們可以快速地對數據進行壓縮處理。壓縮后的數據集是可以在一定程度上反映數據集的趨勢變化規律。但是我們在使用數據進行挖掘有用價值信息的同時，還希望能對未來的趨勢進行預測分析。并且數據集往往具有時間局部性，比如股票數據、生物醫藥數據、臨床數據等。我們所獲得的數據集中的數據，在分析當前數據以及預測未來數據的影響是不一樣的。對于當前數據來說，時間上越靠近的數據對于當前數據的影響越大，時間上越遠的數據對于當前數據的影響越小。對于預測未來數據的走向也是同樣的原理。

2.2 壓縮模型（二）

文獻［15］在對數據進行壓縮的同時，考慮到了數據序列的時間局部性原理。提出了時間影響因子的概念。模型同時使用均值和影響因子，來對數據進行壓縮。

從上面計算均值時的變量設定可以看出，在進行建模時，不是將壓縮起始點放在數據集的開始端點，而是放在了數據集的終端。這是因為如果把起始端放在數據集的開始端點，會導致在計算影響因子參數數值時，反復重復的計算過程。為了避免這個問題，該方法將壓縮起始點放在了數據集的終端。此方法確實考慮了數據序列的時間局部性原理，但是由于壓縮過程中，對數據集是采用自底向上的壓縮方式，不利于處理動態增長的數據問題。

2.3 壓縮模型（三）

針對于以上兩種常見的數據壓縮模型的優缺點，本文提出了壓縮模型（三）。模型既考慮了數據的壓縮要求，同時也兼顧了數據集的時間局部性原理。模型的關鍵在如何選取合適的函數，使得壓縮的模型既能反應原始數據的形態特征，又能兼顧到時間局部性。

函數的選取：如圖1 所示，所選取的函數，函數值應在（0～1）之間且是遞增的。

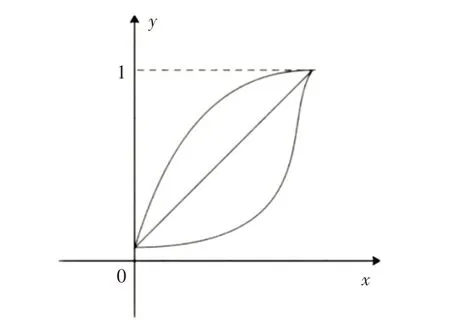
圖1 可選函數模型

具體算法如下：

壓縮模型（三）既可以從數據集的開始端點進行建模，也可以從數據集的尾端開始建模。可以實時在線進行建模原始數據集，方法簡單易用。

2.4 實驗結果

軟件環境：Windows 操作系統，內存4G，64 位操作系統，JAVA語言。

數據來源：本實驗使用“Time Series Classification Website”提供的數據集。

表1 數據集1

表2 數據集2

表3 數據集3

對于三種數據壓縮模型，我們采用壓縮后的兩點數據距離與原始數據的距離差異來進行衡量，如壓縮后的前后兩點數據距離小于某一給定值，而原始數據兩點間的距離卻大于此值，對于此類情況統計后，作為三種模型壓縮效果的比較。

計算公式：壓縮出錯統計=出錯數／總查詢量；在以上提到的標準數據集中的部分實驗結果如圖2所示。

圖2 三種壓縮模型出錯統計圖

從實驗數據可以看出，壓縮模型（三）在三類數據集的統計中，明顯比其他兩種模型出錯量要小。而且相對于壓縮模型（一），壓縮模型（三）考慮了數據集的時間局部性原理，而對于壓縮模型（二），壓縮模型（三）還同時兼顧了數據序列的動態變化情況，對于實時的數據集能更好地進行處理。

3 奇異值識別模型

數據集中的數據千變萬化，有些數據值頻繁出現，表現了數據集的基本趨勢變化，而有些數據雖然不頻繁出現，但在數據的分類聚類、決策分析中更能提供有用的價值，這類數據我們稱之為奇異值。如何能有效地挖掘出奇異值，對于數據集的處理和分析都有非常重要的意義。從于樂軍［16］等發表相關數據序列奇異點數據識別以來，相關研究備受關注。兩種典型的奇異點識別模型如下。

3.1 識別模型（一）

如圖3所示數據序列：

圖3 數據序列簡化模型1

L（（l1，t1），（l2，t2），（l3，t3），（l4，t4），（l5，t5），（l6，t6），（l7，t7），（l8，t8），（l9，t9），（l10，t10））。

識別模型（一）識別奇異點的規則如下。

如圖3，L 共包含有10 個數據點的數據序列。若時間間隔相同，數據序列可記為L（l1，l2，l3，l4，l5，l6，l7，l8，l9，l10）。在10 個數據值中，l2＜l3＜l4，l8＜l9＜l10，則認為l3 和l9 為奇異值點保留。l3＞l4＞l5，l5＞l6=l7，l7＞l8＞l9，則l4，l6，l8 不是奇異值。最終保留奇異值點L（l3，l9）。

以圖3 為例，最終保留的奇異值點可以很好地反映數據集L 的走勢變化，此方法簡單易用。但隨著數據量的不斷增大，識別模型（一）不能有效地去除噪聲。無法有效識別奇異值，濾掉冗余數據。為了更好地去掉一些噪聲數據，可以對識別模型（一）進行改進，如圖4所示。

圖4 中，l2，l3，l4 按照識別模型（一），符合選取的奇異點條件。但是有些奇異點頻繁出現，并不能表現數據集的主要特性，屬于冗余數據。排除這類冗余數據可以考察該奇異點保持的時間（即該奇異點前后兩個奇異點所占的時間段）與數據集總長度的比值，即T1/Length，T2/Length，若T1/Length ＜β（給定的閾值），刪除奇異點l2，若T2/Length＞β（給定的閾值），保留奇異點l3。閾值的設定需根據數據集的實際長度和所在知識領域進行設定，一般小于1。

圖4 數據序列簡化模型2

改進的識別模型（一），可以有效地去除數據集中的噪音數據，但也容易忽略一些表現數據集主要特性的數據。

3.2 識別模型（二）

部分數據集中的數據，雖然不滿足識別模型（一）的奇異值條件，但是也決定了數據集在某一時間段內的趨勢變化，應該作為奇異值被識別，如圖5所示。

l1，l2，l3分別為某數據集的三個連續時間點的數據。l1＞l2＞l3，按照識別模型（一），l2 不是奇異值數據點。但是按照整個數據形態的走向，從t2時刻的l2數據點開始，整個數據集不再按照原來趨勢下降了，而是進入了一個緩慢下降區間。而這一變化正是從l2數據點開始的，那么l2數據點也應該是一個奇異點。杜奕等［17］提出，可以用距離來選取奇異值點。如圖5 所示，若|d2-（d1+d3）/2|＞λ（給定的閾值，根據實際情況調節），則l2被作為奇異值點。

圖5 數據集的簡化模型3

該方法綜合了以上兩種方法的優點，同時又考慮了奇異值點的特殊情況，在消除冗余數據的同時，也能抓住一些表現數據集關鍵特性的奇異值數據。這里λ閾值的設定需要根據實際情況考慮。

3.3 識別模型（三）

本文在綜合了以上幾種識別模型的基礎上，提出了一種新的奇異值識別模型。如圖6所示。

數據集L（（l1，t1），（l2，t2），（l3，t3），（l4，t4），（l5，t5）），若時間間隔相同數據集可記為L（l1，l2，l3，l4，l5），根據識別模型（一），先選出符合條件的奇異值數據。但有些數據雖不滿足模型（一），但是仍然反映了數據值的主要趨勢變化，如何選取此類奇異值數據。本文提出以下方案，如圖6中l2，以l2為基準做一條平行于x軸的直線，l2的前后臨點l1，l3 位于橫線的兩側，此時我們考察，若|（l3-l2）/（t3-t2）-（l2-l1）/（t2-t1）|＞=ε，則l2作為奇異值數據點被識別；如圖6 中l4，以l4 為基準做一條平行于x軸的直線，l4 的前后臨點l3，l5 位于橫線的同側，此時我們考察，若|（l4-l3）/（t4-t3）|＞=ε，或者|（l5-l4）/（t5-t4）|＞=ε，則l4作為奇異值點被識別。

圖6 數據集的簡化模型4

本文提出的識別模型（三），在改進的識別模型（一）的基礎上，對于特殊奇異值數據，提出了一種新的識別方法。該模型能更加有效地識別奇異值數據，并能更好地反映數據集的形態變化。

3.4 實驗結果及分析

本實驗所用數據集為2.4小節中所提供的數據集。

表4 數據集1

表5 數據集2

表6 數據集3

實驗方案：選取的奇異值數量基本一致的情況下，比較奇異值模型與原數據集差異情況。

奇異值數量的變化使用壓縮率進行衡量。例如，原數據集數據個數為α1，選取的奇異值數據個數為α2，壓縮率=（1-α2/α1）*100%。

結果分析：

實驗中使用了奇異值識別模型（一），改進的模型（一），識別模型（二）以及本文中提出的識別模型（三）進行實驗。

如圖7，四種模型在數據集1 上的差異情況比較結果，壓縮率基本相近分別為91%，92%，92%，92%。

圖7 四種模型與原數據集的差異比較圖（數據集1）

如圖8，四種模型在數據2 上的差異情況比較結果，壓縮率基本相近分別為53%，65%，68%，70%。

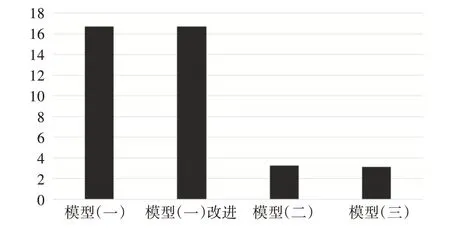
圖8 四種模型與原數據集的差異比較圖（數據集2）

如圖9，四種模型在數據集3 上的差異情況比較結果，壓縮率基本相近分別為78%，92%，91%，92%。

圖9 四種模型與原數據集的差異比較圖（數據集3）

根據以上三個圖的比較，在壓縮率基本相近的情況下，差異情況的比較結果，模型（二）與模型（三）明顯優于模型（一）以及改進的模型（一）。模型（二）與模型（三），在差異情況基本相近的情況下，模型（三）的壓縮率要優于模型（二）。因此，根據實驗結果可以得知，本文提出的模型（三）無論從壓縮率還是差異情況的比較，都要優于其他三種識別模型。

4 結語

本文針對于目前各行業大數據背景，分析了數據集處理的現狀。在分析了幾種已有模型的基礎上，提出兩種數據處理模型，數據壓縮模型（三）以及奇異值數據識別模型（三）。經實驗證明，本文提出的兩種模型，在數據壓縮以及奇異值數據識別研究中是要優于已有的幾種模型。但是，對于奇異值識別模型（三），如何選取合適的ε值，來優化壓縮率以及差異值等指標，是今后需要研究的方向。