黏滯阻尼器對高速列車-大跨斜拉橋耦合系統的減震分析

郭文華，段彬鑫，張廷奎

（1.中南大學 土木工程學院，湖南 長沙 410075；2.中鐵第四勘察設計院集團有限公司 工程經濟設計研究院，湖北 武漢 430063）

我國幅員遼闊，江河密布，且地處跨環太平洋地震帶和地中海-喜馬拉雅地震帶，是一個地震高發國家［1］。隨著我國高速鐵路的蓬勃發展，越來越多的高鐵線路需要跨越大江大河、高山峽谷，甚至海灣、海峽。大跨度斜拉橋憑借其較小自重、較大跨度和較高剛度得到了廣泛的采用。黏滯阻尼器安裝在斜拉橋塔梁或墩梁連接處，減隔震效果顯著，且養護維修方便［2-5］。當地震發生時，盡管橋梁結構自身可能未發生嚴重破壞，但橋梁結構會將地震波通過鋼軌傳遞到列車上，而高速鐵路列車行車速度很快，對線路平順性要求極高，列車也可能因劇烈的振動而脫軌，造成重大安全事故。

國內外學者通過理論分析、數值仿真、模型試驗等方法對黏滯阻尼器的性能、高速列車-大跨度斜拉橋耦合振動、黏滯阻尼器對斜拉橋減震性能等問題進行了深入的研究。李小珍等［6］、郭文華等［7］采用時域分析法，進行了列車經過斜拉橋時的車橋空間耦合振動響應分析，評價了列車的運行安全性。韓艷等［8］、熊建珍等［9］、張騫等［10］研究了鐵路斜拉橋在地震作用或橫風作用下的車-橋耦合動力響應及列車走行性能。朱志輝等［11］分析了高速列車行駛引起的斜拉橋局部振動響應，研究表明大跨度斜拉橋由于整體自振頻率低，車致振動顯著，車-橋耦合問題不能忽視。關于黏滯阻尼器減震性能方面的研究，巫生平等［12］、Geng 等［13］、Soneji 等［14］建立斜拉橋有限元空間模型，對比了不同阻尼器布置方式的減震效果，并以橋梁關鍵部位的抗震能力為指標，對阻尼器的性能參數進行優化。Xu等［15］分別通過振動臺試驗和有限元建模研究大跨斜拉橋的地震響應，振動臺試驗表明黏性阻尼器能顯著減少梁端位移，但對塔底彎矩的減小不明顯。Zhong等［16］采用OPENSEES建立斜拉橋數值模型，通過系統易損性評估方法計算黏滯阻尼器參數優化值。呂龍等［17］通過施加制動力、移動荷載分別模擬列車制動作用和運行作用，探索了塔梁間設置黏滯阻尼器對抑制列車制動和運行引起梁體縱向振動的效果。

以往研究斜拉橋黏滯阻尼器減震效果時往往僅單獨考慮地震作用，一般未建立用彈簧阻尼相連的多剛體列車模型，故未同時考慮高速列車運行引起的車致振動，亦不能對行車安全性進行評估。目前黏滯阻尼器對高速列車-大跨斜拉橋耦合系統減震效果的研究甚少。

本文基于ANSYS 和SIMPACK 聯合仿真分析平臺，以某主跨為400 m 的雙塔雙索面斜拉橋為例，建立地震作用下列車-軌道-斜拉橋-黏滯阻尼器耦合系統動力分析模型，考慮軌道不平順和地震波作為激振源，開展地震作用下車橋耦合系統振動分析，研究地震強度和黏滯阻尼器參數對車橋動力響應的影響。

1 地震作用下列車-軌道-斜拉橋-黏滯阻尼器空間振動分析模型

1.1 列車動力學模型

基于多體動力學建立列車模型，將車輛簡化為由車體、轉向架和輪對等多個剛體以及一、二系懸掛系統組成的多剛體質量彈簧阻尼系統，每個剛體考慮伸縮、橫擺、浮沉、側滾、點頭、搖頭在內的6個自由度。其中，單節車輛模型包含1個車體、2個轉向架和4 個輪對共7 個剛體，共有42 個自由度，其結構模型如圖1所示。圖中：Lc，Lb和Lw分別為車長、轉向架中心距以及軸距，Kps，Cps和Kss，Css分別為一、二系懸掛系統的剛度和阻尼。

圖1 車輛動力學模型示意圖

1.2 橋梁、軌道動力學模型

采用ANSYS 建立大跨斜拉橋和軌道有限元分析模型。主梁、橋塔和輔助墩采用空間梁單元模擬，二期恒載采用主梁換算密度的形式模擬。斜拉索采用只受拉空間桿單元模擬，通過調整初應變設置成橋索力，并采用Ernst公式（1）修正拉索的彈性模量Eeq以考慮垂度效應的影響。

式中：Ec為拉索初始彈性模量；mc，Lh和Ac分別為拉索的兩端點水平投影距離、單位長度質量和橫截面積；FT為拉索索力。

球形鋼支座剛度大、承載能力好，被廣泛應用于鐵路橋梁中。本文對支座不可活動方向的自由度進行主從約束、對可活動的自由度釋放約束，以此模擬球形鋼支座。

將軌道視為由離散彈性點支撐的Euler 梁，同樣用空間梁單元模擬。鋼軌通過扣件連接在主梁上，采用彈簧-阻尼器單元模擬梁軌連接關系，并輸入橫、豎向剛度和阻尼。

1.3 黏滯阻尼器力學模型

本文采用Maxwell非線性力學模型作為黏滯阻尼器計算模型，阻尼力Fd的大小為

式中：C為阻尼系數；α為速度指數，一般取值為0.1～2.0，當α取1 時即為線性黏滯阻尼器；v為阻尼器沖程速度。

當速度指數較小時，黏滯阻尼器阻尼力的非線性特征明顯，阻尼力在速度v接近0 時增大（或減小）較快，易引起仿真計算結果發散，本文采用正則化速度對阻尼器沖程速度進行修正，以提高計算的收斂性，具體如下。

無錫金利達生態科技有限公司是國內專業從事水生態修復工程技術研發及工程材料生產的高新技術企業，是水生態修復整體解決方案提供商。公司主營業務包括水生態修復、生態護岸工程的規劃、設計、咨詢；水生態修復工程技術及產品的研發、生產和銷售；水生態修復工程施工技術的研究、推廣和應用等。公司研發的“生態格網結構”系列產品銷售額在國內市場遙遙領先，成為該行業領軍企業。

式中：Fd′為修正后的阻尼力；vε為設定的1個較小的臨界速度，本文取0.001 m·s-1。

當黏滯阻尼器沖程速度小于vε時對阻尼力進行修正，使其平滑地降至0。

1.4 車-軌-橋耦合系統

輪軌接觸關系是形成列車-軌道耦合系統的關鍵，包括輪軌接觸幾何關系以及輪軌力。其中輪軌力又含輪軌法向力和輪軌蠕滑力，輪軌法向力采用Hertz 彈性接觸理論［18］計算，為考慮輪對的跳軌和擠壓，假設輪軌的接觸點之間有1 個單邊彈簧-阻尼元件，輪軌法向力的表達式為

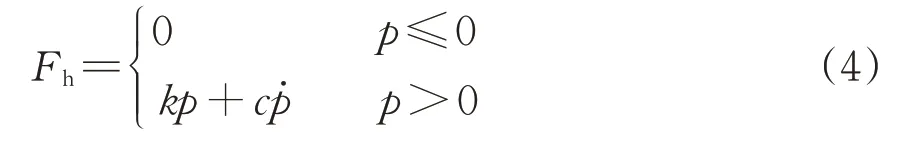
式中：p和分別為輪軌之間法向滲透量和法向滲透速度；k和c分別為彈簧的剛度和阻尼。

采用基于Kalker簡化理論的FASTSIM 算法計算輪軌蠕滑力［19］。

將ANSYS 建立的斜拉橋、軌道有限元模型存儲為編碼數據庫文件（Coded Database File），對模型進行子結構分析，導出包含模型剛度和質量矩陣的子結構矩陣文件（Substructure Matrices File），通過程序接口將其導入SIMPACK，生成對應的橋梁和軌道柔性體模型。以梁軌連接關系和輪軌接觸關系作為橋梁、軌道、列車3 個子系統聯系的紐帶，形成車-軌-橋耦合系統力學模型。

軌道隨機不平順是車橋耦合系統的主要激勵源之一，通過頻域的功率譜密度函數生成空間域的軌道不平順輸入函數，并改變輪軌接觸模塊中所識別的軌道空間初始位置，實現軌道隨機不平順的輸入。

1.5 地震動輸入

在進行車-橋耦合系統地震響應分析時，采用直接求解法，除了地震波的加速度時程，還需知道速度和位移時程。為避免量測地震波加速度時程時包含的噪聲在多次積分后被放大，本文采用最小二乘法對加速度時程進行基線修正，按照位移點在均值線兩側分布均勻和多項式階數盡可能低的準則，采用三次多項式對加速度的均值線進行校正，再對其積分獲得修正后的速度、位移時程曲線［20-21］。以El Centro 為例，修正前后的豎向地震波的加速度、速度和位移時程如圖2—圖4所示。可見，速度和位移時程的偏移在基線修正后有了明顯的改觀。

圖2 修正前后地震波加速度時程曲線

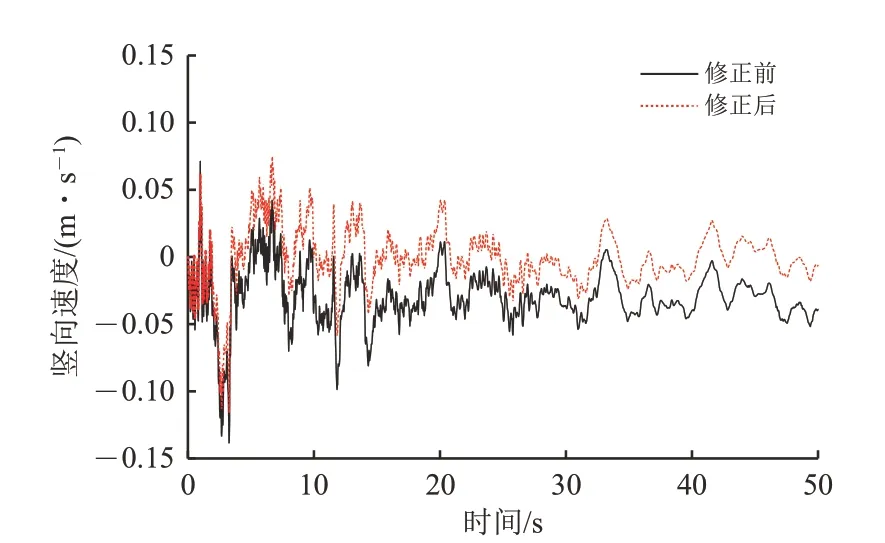
圖3 修正前后地震波豎向速度時程曲線

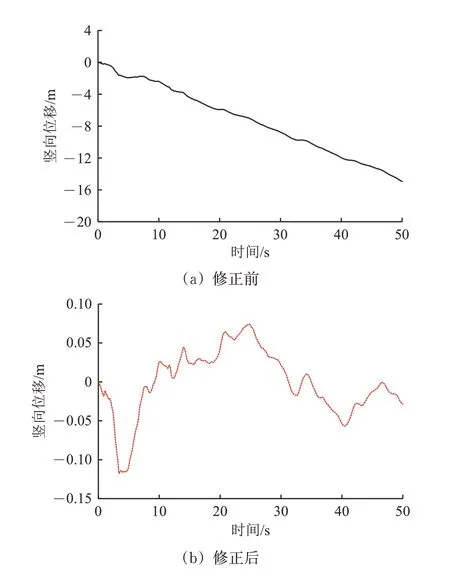
圖4 修正前后地震波豎向位移時程曲線

在SIMPACK 中用一種質量、慣性矩均極小的虛剛體模擬墩底基礎，建立與橋梁-軌道柔性體的約束關系，并讓該虛剛體按照修正后的地震波加速度、速度和位移時程發生運動，從而實現地震動輸入。

2 工程背景與計算條件

2.1 工程概況

以建設中的福廈高鐵某大跨斜拉橋為例，該橋采用70 m+130 m+400 m+130 m+70 m雙塔雙索面鋼混結合梁斜拉橋，建成后將成為世界首座設計時速350 km 的高速鐵路跨海斜拉橋。橋梁兩側邊跨各設有2 個輔助墩，總體布置如圖5所示。主梁為混凝土橋面板與槽型鋼箱梁組成的疊合梁結構，封閉箱形斷面形式，梁寬17 m，風嘴寬4 m，梁高4.25 m。橋塔采用H 形混凝土索塔，塔底以上橋塔全高為160.254 m，主梁以上塔高109 m。主橋共設72 對斜拉索，空間雙索面體系，扇形布置。橋面板及墩塔均采用C50 混凝土，鋼箱梁采用Q345 鋼材，斜拉索采用1 860 MPa 預應力鋼絞線。橋梁阻尼采用Rayleigh 模式，阻尼比取2%。主橋采用半漂浮體系，在輔助墩和主塔的一側設橫向約束、縱向活動，在梁塔之間縱向設置黏滯阻尼器。支座及阻尼器布置方式如圖6所示，圖中：1#，3#，9#和11#為縱向活動支座；2#，4#，10#和12#為雙向活動支座；5#和7#為縱向活動支座并設有縱向阻尼器；6#和8#為雙向活動支座并設有縱向阻尼器。

圖5 斜拉橋總體立面圖

圖6 全橋支座布置圖

2.2 橋梁自振特性

采用ANSYS 和SIMPACK 分別對斜拉橋模型進行模態分析，橋梁自振頻率及陣型見表1。由表1可知：ANSYS與SIMPACK 2種軟件對于橋梁有限元模型自振特性的計算結果高度吻合，表明本文采用ANSYS 橋梁有限元模型生成柔性體輸入文件，并導入到SIMPACK 平臺完成橋梁建模的方法是正確的；該橋第1 階模態為主梁1 階橫彎，橫彎振型先于豎彎振型出現，表明橋梁的橫向剛度要弱于豎向剛度，這符合一般鐵路斜拉橋的特征。

表1 泉州灣特大橋有限元模型前8階自振特性

2.3 車輛和軌道模型參數

在進行高速列車-大跨斜拉橋耦合系統動力仿真分析時，采用ICE3 動車組，單列8 車編組（拖車+6×動車+拖車），車輛參數見文獻［22］。軌道模型采用軌距為1 435 mm 的標準板式無砟軌道，標準60 km·m-1鋼軌，扣件間距為0.6 m，扣件橫、豎向剛度分別取60 和120 MN·m-1，扣件橫、豎向阻尼分別取120和150 kN·s·m-1。軌道不平順采用德國低干擾譜。

2.4 地震激勵參數

本文采用修正后El Centro 地震波的水平南北向分量以及豎向分量作為車-軌-橋耦合系統動力分析的地震波。用橫橋向加速度波幅值表示地震強度，豎橋向加速度波幅值取為橫橋向的0.5倍。

3 地震強度對耦合系統動力響應的影響

為分析地震強度對車-軌-橋耦合系統振動響應的影響，假定車速為300 km·h-1，選取地震強度范圍為0.06g～0.20g，按每隔0.02g為1 個工況，分別計算不同地震強度下的列車-橋梁空間振動響應，計算中假定橋梁結構始終處于彈性階段。不同地震強度下列車和橋梁最大動力響應如圖7所示。

圖7 不同地震強度下列車和橋梁動力響應

計算結果表明：隨著地震強度的增加，列車的脫軌系數、輪重減載率、輪軸橫向力和車體加速度呈增長趨勢，列車脫軌系數和輪軸橫向力在地震強度超過0.10g后增速明顯加快，并且超過了安全限值，列車行車的安全性無法保證；橋梁主跨跨中位移、加速度均不斷增大；無橫向阻尼器時，地震作用對耦合系統橫向響應的影響大于豎向。

4 黏滯阻尼器參數對耦合系統動力響應的影響

4.1 橫向黏滯阻尼器布置方案

原設計方案主梁在縱橋向為半漂浮體系，梁塔之間僅設有縱向阻尼器限制主梁位移（見圖6），考慮到橫向地震可能對高速行車安全產生更不利影響，為研究黏滯阻尼器在橫向減震體系中的作用，故解除輔助墩3#和9#處、主塔5#和7#處支座的橫向約束，并采用橫向黏滯阻尼器替換。

4.2 橫向黏滯阻尼器參數的影響

黏滯阻尼器的耗能能力與速度指數α和阻尼系數C密切相關。為此，針對橫向阻尼器布置方案開展阻尼器參數敏感性分析。保持列車車速為300 km·h-1，地震強度為0.1g不變，選擇黏滯阻尼器的速度指數α分別為0.2，0.3，0.4，0.6 和0.8，阻尼系數C分別為2 000，4 000，6 000，8 000和10 000 kN·（m·s-1）-α，共組合25 個工況，進行耦合系統在地震作用下的動力響應分析。圖8和圖9分別給出了不同阻尼系數C、不同速度指數α組合下列車和橋梁的動力響應。

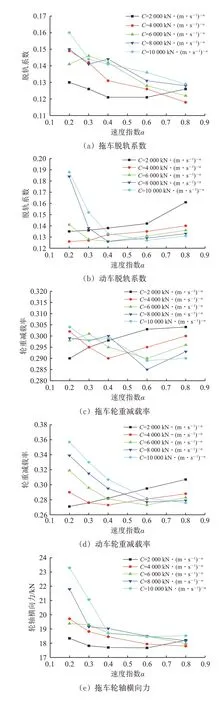
圖8 列車動力響應與阻尼器參數的關系

圖9 橋梁動力響應與阻尼器參數的關系

與按原設計方案的車橋動力計算結果對比可知：安裝橫向黏滯阻尼器之后，地震作用下車橋耦合系統的橫向動力響應均有明顯降低。對于給定的阻尼系數C，拖車的脫軌系數、輪軸橫向力大致隨速度指數α的增大而減小；動車的脫軌系數、輪軸橫向力及動、拖車的輪重減載率當阻尼系數C＜4 000 kN·（m·s-1）-α時隨速度指數α的增大而增大，而當C≥4 000 kN·（m·s-1）-α時隨速度指數α的增大先減小后增大；隨著速度指數α的增加，主梁跨中橫向位移大致呈減小趨勢，當位移降低至60 mm附近時變化不再明顯；主梁跨中橫向加速度在C處于［4 000，8 000］kN·（m·s-1）-α區間時隨著速度指數α的增加先減小后增大，并且在α 處于［0.4，0.6］區間時取得最小值。

對于給定的速度指數α，拖車的脫軌系數、輪軸橫向力大致隨阻尼系數C的增大而減小；當α＜0.4 時，動車的輪重減載率隨阻尼系數C的增大而增大，動車的脫軌系數和輪軸橫向力隨阻尼系數C的增大先減小后增大，并且都在C處于［4 000，8 000］kN·（m·s-1）-α區間時取得最小值；當α＞0.4 時，動車的脫軌系數和輪軸橫向力隨著阻尼系數C的增大而減小；拖車的輪重減載率隨阻尼系數C增大的變化規律不明顯；隨著阻尼系數C的增大，主梁跨中橫向位移大致呈增大趨勢，跨中橫向加速度在α處于［0.3，0.8］區間時先減小后增大。

從參數分析可知，當速度指數α在［0.3，0.6］區間內，列車輪重減載率、動車脫軌系數和輪軸橫向力基本達到曲線谷底，且在該區間內C在［4 000，8 000］kN·（m·s-1）-α時取到最小值，拖車及橋梁的動力響應也位于較低水平，因此從減小耦合系統振動響應的角度，阻尼器參數的合理取值為α在［0.3，0.6］區間，C在［4 000，8 000］kN·（m·s-1）-α區間。

為從列車減震效果的角度給出阻尼器的最優設計參數，將針對列車各響應指標（包括動車和拖車的脫軌系數、輪種減載率、輪軸橫向力）的減震率平均值最小作為參數優化目的，對于某一響應指標的減震率β定義為

式中：Dnone和Ddamper分別為無橫向阻尼器和設置橫向阻尼器時系統的地震響應。

基于設置橫向阻尼器方案25 個工況的計算數據，求得滿足要求的最優參數組合為α取0.6，C取8 000 kN·（m·s-1）-α，此時減震率平均值為38.3%。

5 結 論

（1）隨著地震強度的增加，耦合系統動力響應均會增大，地震強度對橫向響應的影響大于豎向。

（2）斜拉橋設置橫向黏滯阻尼器后，車輛橫向動力響應的峰值顯著降低，主跨跨中橫向位移、橫向加速度位移峰值也有所降低。

（3）隨著速度指數α的增加，耦合系統各橫向動力響應均有明顯的變化，所有列車橫向動力響應相比普通支座工況均有明顯下降，大部分橋梁橫向響應相比普通支座工況均有明顯下降；隨著阻尼系數C的增加，列車橫向動力響應相比普通支座工況也均有明顯下降。

（4）能起到減小耦合系統振動響應的阻尼器參數取值為［0.3，0.6］，C在［4 000，8 000］kN·（m·s-1）-α；耦合系統減震效果最優的阻尼器參數組合為α取0.6，C取8 000 kN·（m·s-1）-α，此時減震率平均值為38.3%。