基于0-1 規劃的生產企業原材料訂購與運輸研究

張倩男， 李 圓， 丁國威， 劉 通， 田夢真

（1.商丘工學院 基礎教學部， 河南 商丘 476000； 2.黃河交通學院 基礎教學部， 河南 焦作 454002；3.黃河交通學院 機電工程學院， 河南 焦作 454002）

1 問題重述

某建筑和裝飾板材的生產企業所用原材料為A、B、C 三種類型，該企業需要根據產能要求確定需要訂購的原材料供應商和相應每周的原材料訂購數量，確定轉運商并委托其將供應商每周的原材料供貨量轉運到企業倉庫。分析某企業近5 年402 家原材料供應商的訂貨量和供貨量數據。2021 年全國大學生數學建模競賽C 題[1]旨在引導學生通過背包模型來研究企業原材料訂購與運輸的優化問題。

1）對402 家供應商的供貨特征進行量化分析，建立反映保障企業生產重要性的數學模型，在此基礎上確定50 家最重要的供應商，并在論文中列表給出結果。

2）參考問題1，該企業應至少選擇多少家供應商供應原材料才可能滿足生產的需求？針對這些供應商，為該企業制定未來24 周每周最經濟的原材料訂購方案，并據此制定損耗最少的轉運方案。試對訂購方案和轉運方案的實施效果進行分析。

2 基本假設及符號說明

2.1 基本假設

假設生產企業在第一周初始時原材料的儲存量為零；轉運損耗率小與轉運公司實力成負相關；企業要保持大于等于滿足兩周生產需求的原材料庫存量；假設原材料只有轉運損耗，沒有庫存損耗。

2.2 符號說明（見表1）

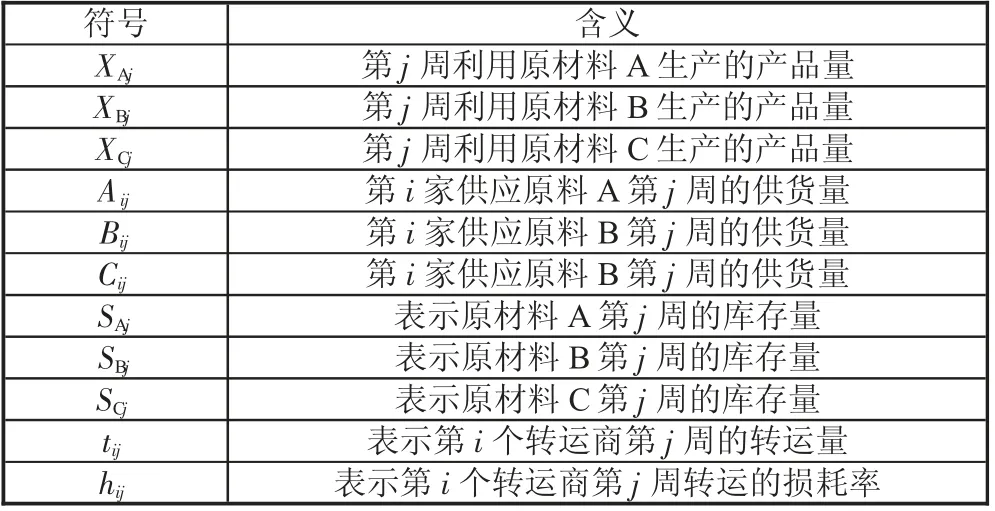
表1 符號說明

3 模型的建立與求解

3.1 問題一建模與求解

3.1.1 利用SPSS 分析供應量與采購量相關性

求出402 家每一家供應商的總供貨量和企業對應每一家供應商的總采購量，并分別計算其平均值，進而求出402 家供貨商的供貨量的標準差和企業采購量的標準差，通過平均數和標準差進行SPSS 相關性分析，衡量兩個變量的相關程度。結果見表2，可知總供貨量和企業總采購量的相關性系數為0.946，說明總供貨量和企業總采購量之間存在極顯著的正相關關系。

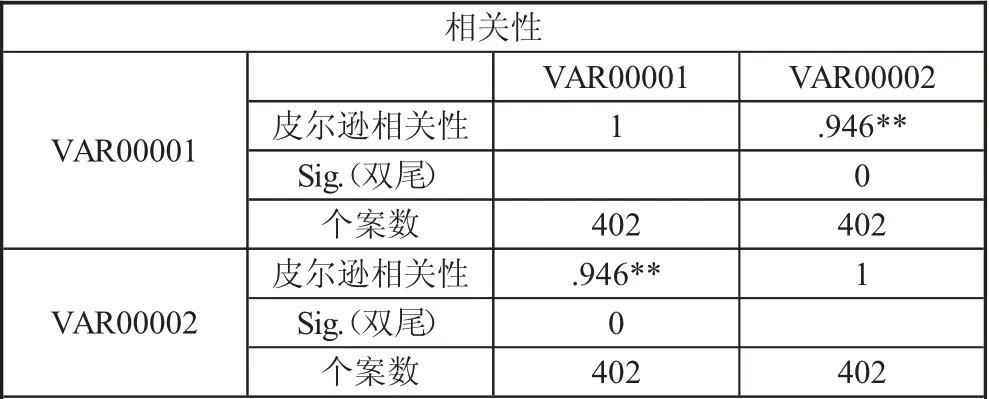
表2 供貨量和采購量相關性

3.1.2 用層次分析法分析權重

利用EXCEL 對附件1 中402 家供貨商的供貨量和企業在每一家供貨商的采購量進行求和處理，對總供貨量和總采購量進行求差處理，以選擇合適的供貨商為目標層，以總供貨量、總采購量、總供貨量與總采購量的差值為準則層，采用層次分析法分析三者的權重，通過權重比較，篩選出50 家最重要的供貨商。由于附件1 中的數據過大，不易分析，為使得方便求解，因此令總訂貨量小于總供貨量為數值3，等于為數值2，大于為數值1 建立量化矩陣。

3.1.2.1 遞階層次結構的建立

為構建合適的層次結構，對各項指標進行分析，最終選擇以選擇合適的供貨商為目標層，以總供貨量、總采購量、總供貨量與總采購量的差值為準則層，以402 家供貨商為方案層建立層次結構模型[2]。

3.1.2.2 構造比較判斷矩陣

遞階層次結構確定后，上下兩個層次的關系隨之確定，以上一層的特征值為準則，確定下層相對于上層的重要性進而賦予其相應的權重。因為本文的數據過多，指標準則少，元素的權重不能直接接得出。因此采用兩兩比較方法對權重進行計算，收集各項指標的原始數據，構建比較判斷矩陣：R=（rij）

若rij＞0、rij=1/rji、rii=1（i，j=1，2，…，n），則比較判斷矩陣：

3.1.2.3 單準則下的排序及一致性檢驗

由于準則控制著下一層的因素，因此這些要素間可以構成一個條件判斷矩陣，本文采取特征根方法計算權重，該方法可以保證得到的排序向量有正值性和唯一性。

1）最大特征根。設n 階方程R＞0，λmax為R 的最大特征根。即：

2）判斷矩陣。通過資料[3]發現矩陣R 的階數n 不超過R 的最大特征值λmax，即：

3）歸一化。將判斷矩陣列向量歸一化：

根據以上式子，可得到R 的最大特征值為：

式中：（RW）i為RW 的第i 個分量。

對附件1 數據進行量化分析后，將所得數據代入以上算法，結果見表3，分析發現一致性檢驗結果通過，則可以認為結果是準確的。

表3 一致性結果

三項指標的權重：W1表示總供應量在數據中的權重，W2表示總訂單在數據中的權重，W3表示差值在數據中的權重，利用MATLAB 求解，結果分別為0.648 33、0.122 02、0.0.229 65。

3.1.3 篩選供貨商

供貨商的供貨量是一個企業生產中最重要的體現之一，假如供貨量達不到企業生產的最低消耗量，那么生產活動將會停止，進而影響生產效益。利用EXCEL 對表4 中的權重比從大到小排序，選出前50名的供貨商，結果見表4。

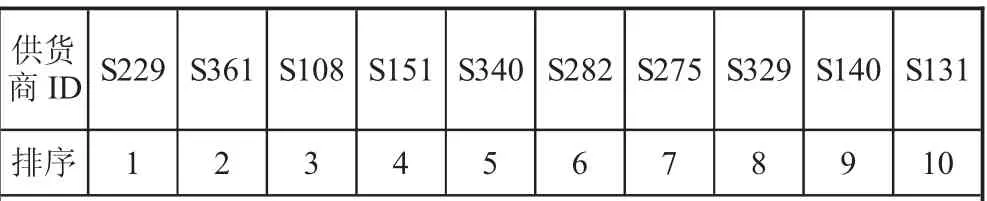
表4 供貨商部分名單

3.2 問題二建模與求解

3.2.1 0-1 規劃模型求供應商數量

參考問題一，在402 家供應商中選出了最重要的50 家供應商，依據是這50 家供應商的供貨量相比于其他供應商要多。因此該問所求就是供貨量最多，并且能滿足企業生產的最少供應商數量。將所有供應商進行分類，按照同種原材料分成一類，共分成A、B、C三大類，在這三大類中對供應商進行選擇，因此每一類中的每一家供應商都有兩個選擇，采用0-1 整數規劃模型對三類原材料供應商建立相對應的模型。設：

1）第j 周利用原材料A、B、C 生產的產品量：

2）原材料第j 周的庫存量：

3）第i 家原材料的供應量和庫存量與產能的關系：

4）因為所求為最少供應商數量，所以目標函數為：

以最少供應商數量為目標函數，以原材料的供應量和庫存量與產能的關系為約束條件建立0-1 規劃模型。

3.2.2 整數規劃求解原材料訂購

在上一小問求得的供應商基礎上，對供應商的三種原材料價格進行分析，采取最經濟的采購方式，使得生產效益達到最大化。從題目中可知A 和B 類原材料的采購單價分別比C 類原材料高20%和10%，并且三類原材料運輸和儲存的單位費用相同。假設C類原材料單價為1，則A 類為1.2，B 類為1.1。用整數規劃模型對三類原材料供應商建立相對應的模型。設

1）第j 周利用原材料A，B，C 生產的產品量：

2）原材料A 第j 周的庫存量：

3）第i 家原材料A 的供應量和庫存量與產能的關系：

4）因為所求為最少采購成本，所以目標函數為：

以原材料最低采購成本為目標，各周利用原材料A、B、C 生產的產品數量和選擇哪家供應商為決策變量，通過上述各約束條件，建立整數規劃模型。

3.2.3 目標規劃選擇損耗最小方案

在選擇成本最小的采購方式上，對運輸途中的損耗進行分析。在實際運輸過程中，材料的損耗不可避免，因此生產企業收到的材料并不是轉運商轉運的全部供貨量，而是除去損耗后的接收量［接收量=供貨量×（1- 損耗率）］。為使得原材料接收量達到最大，那么在轉運途中的損耗量=供貨量×損耗率必須要達到最小，另外接收量要滿足正常的生產活動。

建立目標規劃模型。

1）通過對庫存量分析，保證庫存量在這24 周內有余量，對其建立規劃方程：

2）從三種原材料中選擇合適的比例，保證產能可以達到：

3）總接收量和總生產產能的關系：

4）損耗最小方程：

當hij=0 時tij=0，假設A、B、C 三種材料的第一周庫存量均為0。

5）A、B、C 三種原材料的供應商數量受到采購成本的限制，所以該問題中需要此目標函數確定三種原材料的供貨量：

通過以上公式建立多目標規劃模型[4]，求解損耗量最低時的材料轉運方案。

3.2.4 問題二結果分析

1）若想選擇最少的供應商來完成原材料供應需求，則需要選擇供應量數量排名較高的供應商，此處可參考問題一的供應商排名，其選擇結果見圖1。

通過MATLAB 求解可得到：至少需要23 家供應商才能滿足需求，結果見表5。

表5 23 家供應商名稱

2）訂購方案：若要選擇未來24 周每周最經濟的原材料訂購方案，則在滿足生產需求的情況下可多訂購B 類原材料、少訂購C 類原材料，訂購方案見圖2。

3）轉運方案：在原材料訂購最經濟的情況下，選擇損耗率最小的轉運方案，可優先選擇T1、T2、T3 來轉運原材料，T5、T6、T7、T8 轉運商因為其轉運過程中的損耗率較高，可以不考慮，其結果見圖3。

4 結論

根據原材料的供應鏈管理，考慮包含生產企業、原材料供應商、轉運商的三層供應鏈中的生產和訂購問題。

1）對供應商的供貨特征進行量化分析，利用SPSS軟件找出影響企業重要性的因素，建立了層次分析模型，利用MATLAB 軟件求解，確定了保障企業生產的50 家最重要的供應商。

2）在滿足生產需求的前提下，以供應商最少為目標函數建立0-1 規劃模型，通過MATLAB 對模型進行求解，選出23 家供應商。分別以總成本降為最低、轉運損耗率最小為目標函數，分別建立目標規劃模型，得到最優的訂購方案和最優的轉運方案。