基于影響線輕荷載試驗的橋梁承載力評估方法研究*

王珊珊，張榮鳳，亓興軍，趙 奇

(1.山東高速集團有限公司，山東 濟南 250098； 2.山東建筑大學交通工程學院，山東 濟南 250101)

0 引言

橋梁運營期間，受到自然災害或人為等因素影響，導致材料老化、結構受損，對橋梁的安全性和承載力產生威脅[1-2]。我國頒布了JTG/T J21-01—2015《公路橋梁荷載試驗規程》，美國、加拿大等國頒布了新的橋梁承載力使用規范，規范中給出的評估模型可用來評價各種類型的橋梁[3-5]。由此可見，橋梁承載力評估是國內外橋梁界關注的問題，而橋梁荷載試驗是公認的評價橋梁承載力的有效方法，但傳統的荷載試驗具有以下缺點：編制試驗方案時為了滿足加載效率，需不斷調整加載車輛自重及位置；試驗過程中需封閉交通，現場也需工程師指揮調配加載車，整個試驗流程操作繁瑣、耗費大量人力物力。

常丁通過分析校驗系數，得出其可由結構的抗彎剛度表示，混凝土結構的撓度隨外荷載變化，傳統荷載試驗采用逐級加載方式，這是一個外荷載變化的過程，因此每一級加載工況下，橋梁撓度變化，校驗系數也變化；通過對分級過程中的校驗系數進行研究，找到分級加載下校驗系數的相關性，便可由輕荷載下校驗系數計算重荷載下的校驗系數，因此研究了基于輕荷載試驗的梁橋承載力快速評定方法。輕荷載試驗是指由少量試驗車輛進行的試驗，重荷載試驗是指滿足試驗規程中荷載效率 0.85～1.05 的試驗，通過校驗系數分析理論，建立不同荷載效率下結構校驗系數的函數關系，給出由輕荷載校驗系數得到重荷載校驗系數的計算方法[6]。林迪南根據常丁的試驗方法，對橋梁進行了快速評估，并將校驗系數差值范圍及相對差值-對應荷載效率回歸方程稱為“常丁模型”[7]。袁治和杜晶采用輕荷載試驗研究了荷載分布系數，為橋梁橫向聯系損傷提供指導[8-9]。陳彥坤根據不同橋型組配出橋梁檢測適合的儀器方案，再基于輕荷載試驗完成橋梁承載力的快速評定，提高了檢測效率[10]。輕荷載試驗以其快速完成荷載試驗、提高工作效率、節省資源等優點，成為快速評估橋梁承載力新的研究方向。

準靜力影響線可通過緩慢勻速跑車的方式來獲取[11]，單輛跑車沿著指定路線緩慢駛過橋面便可完成試驗，獲得數據量大且穩定，相對于傳統荷載試驗來說，影響線跑車試驗快速便捷，單輛跑車可作為輕荷載加載，根據“常丁模型”，可用于新橋評定或主梁處于彈性范圍內的舊橋承載力評估。本文以影響線跑車作為輕荷載，根據“常丁模型”的計算方法，對某高速公路的佟家莊大橋承載力進行快速評估。

1 輕荷載試驗方法

在編制橋梁荷載試驗方案時，往往要根據控制荷載進行逐級加載，這使得在試驗中因逐級加載而耗費大量時間。因此，從減少荷載試驗車輛數量著手，常丁提出基于輕荷載的加載方式[6]。借鑒“常丁模型”輕重荷載校驗系數轉變方法，本文基于影響線輕荷載試驗方法的思路為：利用準靜力影響線測試車作為輕荷載加載，采集1輛測試車加載工況下橋梁的撓度和應變影響線數據；建立橋梁有限元模型，計算輕荷載下靜載試驗的加載效率與校驗系數，利用“常丁模型”計算轉變為滿足加載效率 0.85～1.05 的傳統荷載試驗校驗系數，結合現行規范對新橋或仍處于線彈性范圍內舊橋承載力進行快速評估。

校驗系數在橋梁承載力評定中是一個重要指標，其數學公式為：

(1)

式中：Se為試驗荷載作用下測量的結構彈性撓度(或應變)值；Ss為試驗荷載作用下計算的結構撓度(或應變)值。

由文獻[6]可知，將材料力學中應變的計算公式 (2)代入式(1)，得到校驗系數由剛度定義的表達式(3)：

(2)

(3)

式中：M為梁上荷載在某一截面處引起的彎矩；y為該點到截面中性軸的距離；Se為試驗荷載作用下測量的結構彈性應變值；Ss為試驗荷載作用下理論計算結構最大應變值；EI為梁的彎曲剛度；EsIs為理論抗彎剛度；EeIe為實測應變對應抗彎剛度。

由式(2)與式(3)可知，結構的應變校驗系數從形式上可由應變值轉變為剛度值，其可由結構的理論計算抗彎剛度與實測應變對應抗彎剛度的比值表示。

如圖1所示，某一集中力作用在簡支梁上，由結構力學得到簡支梁的撓曲方程式(4)：

圖1 受集中力作用的簡支梁

(4)

將式(4)代入式(1)，得到撓度校驗系數也由剛度定義，其計算公式如下：

(5)

撓度校驗系數從形式上看可由應變值轉變為剛度值，同理，撓度校驗系數也可由理論抗彎剛度與實測撓度對應抗彎剛度的比值定義。因此，校驗系數與結構的剛度有關，若結構處于線彈性范圍內，校驗系數為常數，與加載車自重和位置無關；但對橋梁進行荷載試驗時，分級加載是外荷載遞增的過程，實際荷載效率也隨之變化，于是得到：每級荷載加載工況下，加載效率與校驗系數間存在一定的函數關系；重荷載與輕荷載下校驗系數間也存在一定的函數關系，如此通過輕荷載的加載效率便可求得重荷載下的結構校驗系數，結合規范便可實現對橋梁承載力的評估。文獻[6]通過對103座中小跨徑橋梁(預應力混凝土橋66座，鋼筋混凝土橋37座)荷載試驗的分級加載數據統計分析，得出鋼筋混凝土梁橋的校驗系數差值范圍。在分析校驗系數的關系中，<0.85的荷載效率分為5個檔次范圍，分別為0.75～0.84，0.65～0.74，0.55～0.64，0.45～0.54，0.3～0.44。以荷載效率作為分類標準，采用做差值的方法分析，對重荷載與所劃分的輕荷載下的校驗系數進行計算，得到如下公式：

Δa=ζ-ζn

(6)

(7)

式中：Δa為絕對差值；ζ為在荷載效率0.85～1.05內的應變(或撓度)校驗系數；ζn為在<0.85的5個荷載效率范圍內的應變(或撓度)校驗系數，n=1～5；Δr為相對差值。

利用四分位法對所統計橋梁的各荷載效率下對應的結構應變(或撓度)校驗系數差值進行分析，得到校驗系數差值范圍，建立相對差值與其相對應的荷載效率間的回歸方程。聯合差值范圍與式(6)和式(7)計算可得到重荷載效率下的校驗系數，其中鋼筋混凝土梁橋的Δr-η回歸方程如表1，2所示[6]。

表1 鋼筋混凝土梁橋應變校驗系數差值范圍

表2 鋼筋混凝土梁橋撓度校驗系數差值范圍

2 基于影響線跑車加載的橋梁承載力評估

2.1 工程概況

某高速公路的佟家莊大橋全長270.66m，跨徑組合為13×20m，橋面總寬度為2×11.2m，橫向布置為 0.5m 護欄+10.25m凈寬+1.5m分隔帶+10.25m凈寬+0.5m護欄。上部結構為C40簡支鋼筋混凝土 T形梁，下部結構為肋板臺、柱式墩、樁基礎。該橋于1993年建成通車，設計荷載等級為汽-20、掛-100。現橋面鋪裝為13cm厚C40混凝土鋪裝層+7cm厚瀝青鋪裝層。該橋整體外觀及橋梁橫斷面、立面如圖2～4所示。

圖2 佟家莊大橋整體外觀

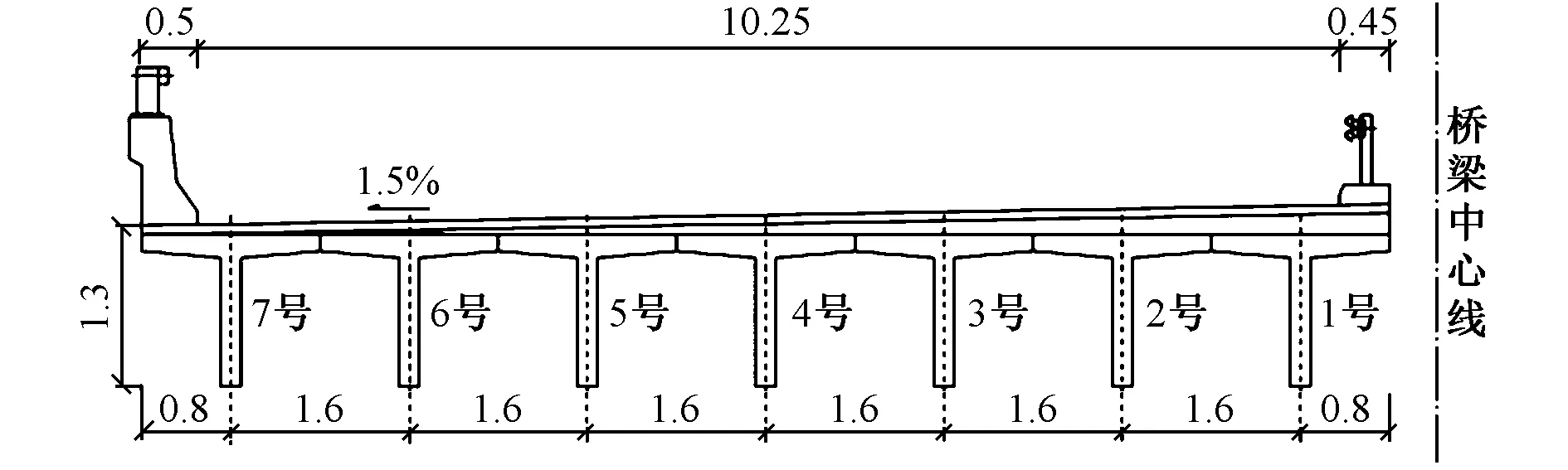
圖3 橋梁橫斷面(單位：m)

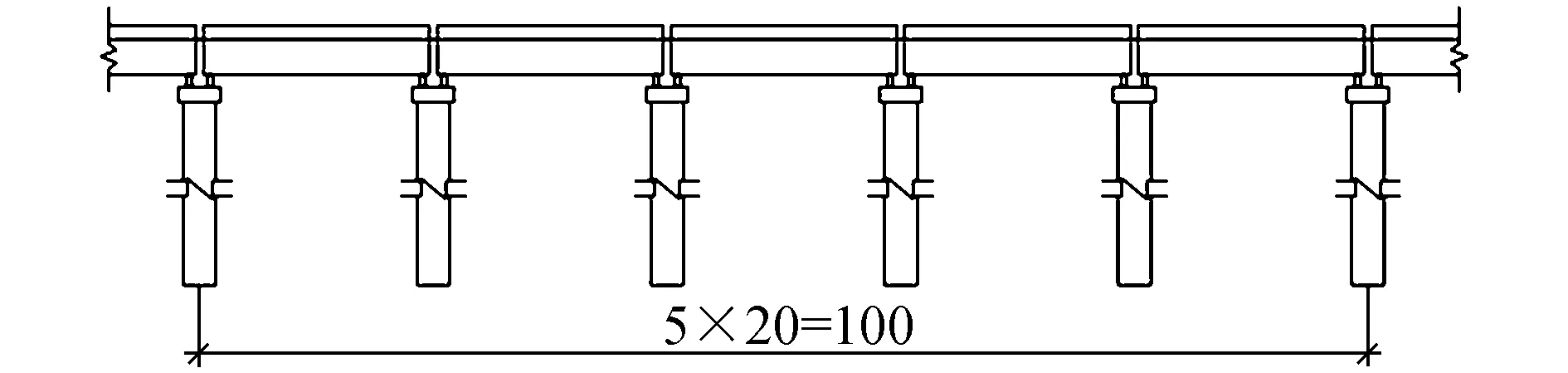
圖4 5×20m T梁連接示意(單位：m)

2.2 試驗工況

影響線測試分為2個工況：②工況1 撓度和應變影響線測試，測試車車道距離橋梁內側2.4m，測試車以<5km/h的速度勻速通過橋梁，連續采集記錄數據；②工況2 撓度和應變影響線測試，測試車車道距離橋梁內側4.2m，測試車以<5km/h的速度勻速通過橋梁，連續采集記錄數據。其中，測試車輛軸距分別為1.45，4.10m，軸重分別為13.46，13.46，9.94t，影響線測試工況及跨中截面測點布置如圖5所示。

圖5 影響線測試工況及測點布置(單位：m)

2.3 承載力評估

利用輕荷載試驗進行橋梁承載力評定，首先計算輕荷載加載效率。利用ANSYS有限元軟件建立試驗橋梁有限元模型，主梁采用shell63單元，實橫梁采用beam4單元，變厚度混凝土鋪裝采用solid65單元，厚度從橋面外側0.08m漸變至橋梁內側0.248m，形成1.5%橫坡，支座采用combin單元模擬，豎向剛度為1×1010N/m；通過耦合模擬橫向連接；支座設置在距梁端0.25m處，采用簡支約束。施加掛-100設計荷載，計算跨中截面撓度效應值，施加設計荷載的有限元計算模型如圖6所示，撓度變形如圖7所示。

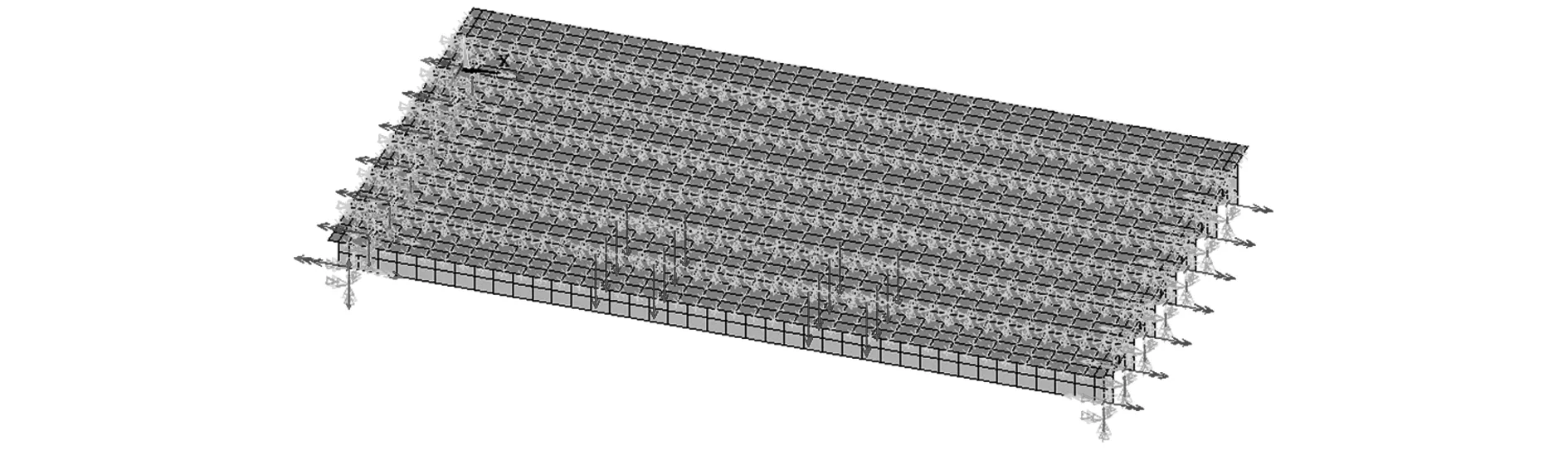
圖6 設計荷載計算模型

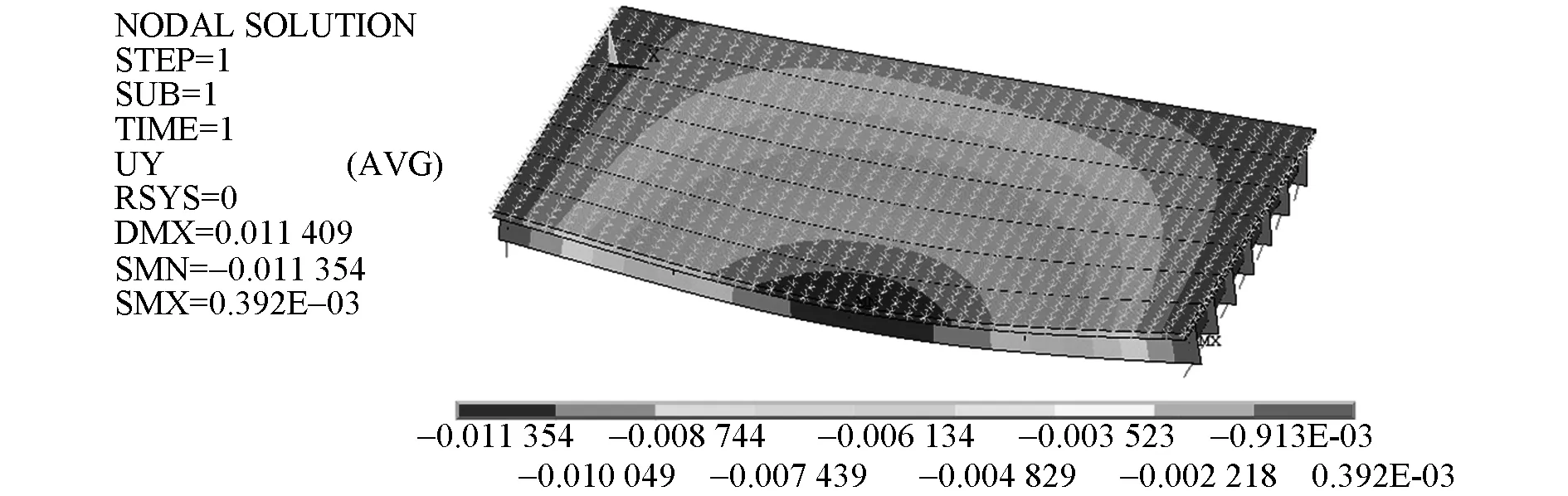
圖7 設計荷載作用下撓度變形

影響線測試車加載后提取各測點撓度值，根據荷載試驗規程，利用跨中整體截面的撓度值計算加載效率，得到影響線測試工況1，2的荷載效率，如表3所示。

表3 輕荷載試驗荷載效率系數

由表3可知，工況1，2的撓度輕荷載效率在0.3～0.84，可采用Δr-η回歸方程進行計算。采用ANSYS有限元軟件計算影響線測試工況1，2的理論計算值，根據跨中截面的1～4號和7號測點的理論值與實測值，計算基于輕荷載的應變校驗系數和撓度校驗系數，結果如表4，5所示。

表4 輕荷載試驗下跨中截面應變校驗系數

表5 輕荷載試驗下跨中截面撓度校驗系數

由表4，5可知，工況1的輕荷載應變校驗系數分布范圍為0.53～0.98，平均值為0.80，輕荷載撓度校驗系數分布范圍為0.40～0.71，平均值為0.63；工況2的輕荷載應變校驗系數分布范圍為0.72～1.02，平均值為0.85，輕荷載撓度校驗系數分布范圍為0.51～0.70，平均值為0.62。根據輕荷載加載效率及校驗系數回歸方程，將2個輕荷載效率下的校驗系數轉變為滿足荷載效率0.85～1.05下的校驗系數，轉變后2個工況的應變校驗系數與撓度校驗系數數據如表6所示。

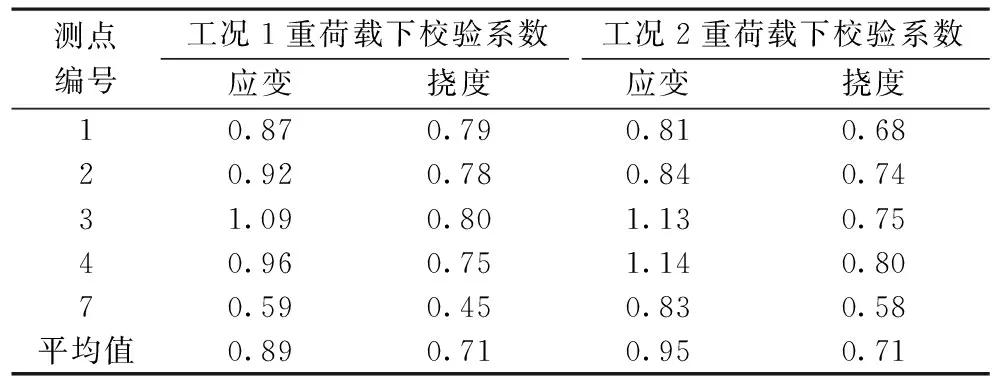
表6 輕荷載校驗系數轉變為重荷載校驗系數數據

統計輕荷載與重荷載校驗系數各自的分布范圍，結果如表7，8所示。

表7 應變校驗系數分布范圍

表8 撓度校驗系數分布范圍

由表6～8可知，由輕荷載下校驗系數轉變為重荷載下校驗系數后，各測點的撓度校驗系數均<1，說明橋梁整體結構處于彈性工作狀態，但3，4號測點應變校驗系數存在>1的情況，表明該橋的承載力不滿足設計要求。

3 影響線輕荷載試驗與傳統試驗對比

3.1 傳統荷載試驗

選擇佟家莊大橋第7跨跨中截面作為控制截面，7片梁底分別布置撓度傳感器及應變傳感器，所有傳感器布置如圖8所示。

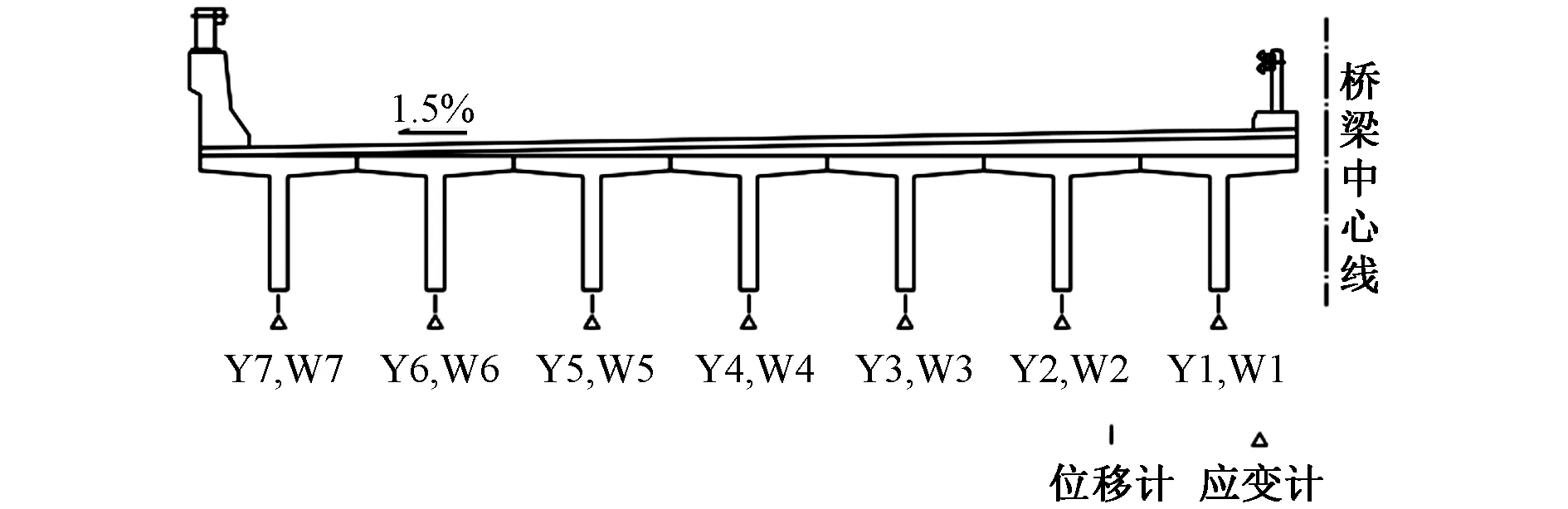
圖8 跨中截面測點傳感器布置

荷載試驗選擇3輛三軸車作為加載車，各加載車的車輛信息如表9所示，荷載試驗加載車平面布置及現場試驗如圖9所示。

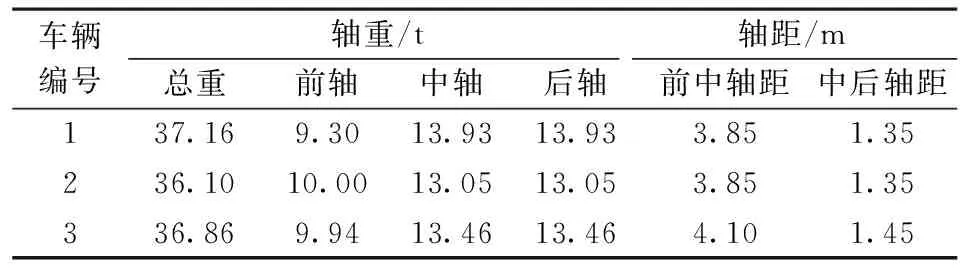
表9 加載車輛尺寸及軸重

圖9 加載車輛平面布置(單位：m)

在試驗荷載作用下，試驗跨截面實測應變、撓度數據如表10，11所示。

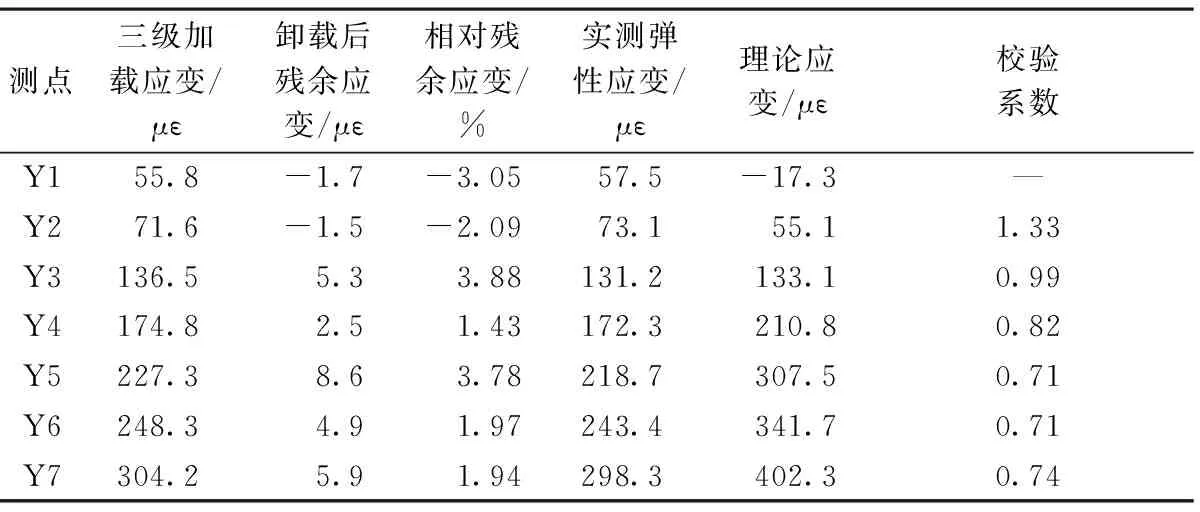
表10 跨中截面實測應變

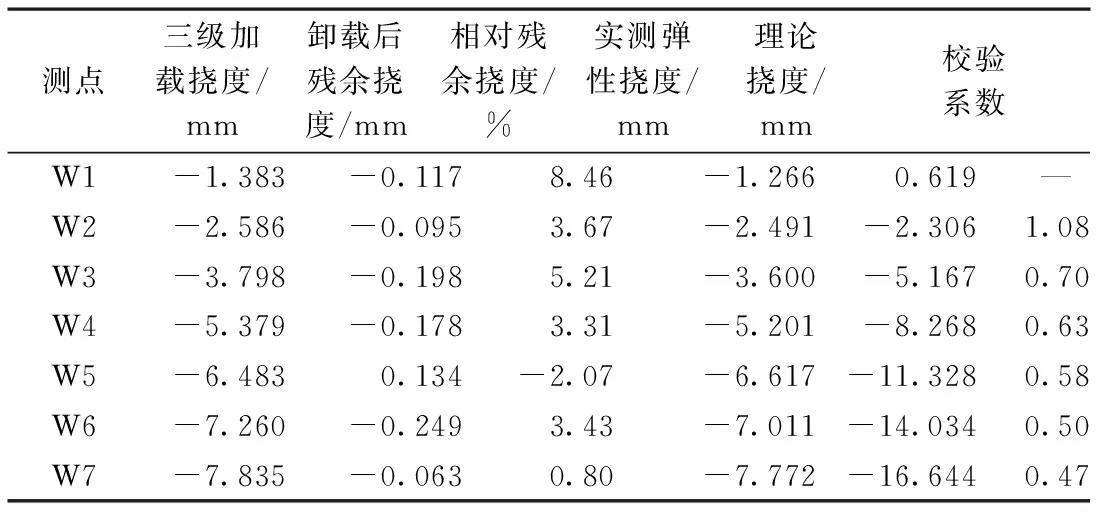
表11 跨中截面實測撓度

由表10，11可知，跨中截面2號測點應變校驗系數與撓度校驗系數均>1，3～7號測點應變校驗系數分布范圍為0.71～0.99，撓度校驗系數分布范圍為0.47～0.70，相對殘余應變最大值為3.88%，相對殘余撓度最大值為8.46%；荷載試驗下最大殘余系數<20%， 表明橋梁結構處于彈性工作狀態，2號測點應變校驗系數與撓度校驗系數均>1，不滿足承載力評定規程中靜力荷載試驗校驗系數<1的要求，表明橋梁實際承載力不滿足設計要求。

3.2 兩種試驗結果對比

現場試驗時，傳統荷載試驗加載車輛位于橋梁外側，影響線測試路徑靠近橋梁內側，且影響線測試工況僅采集1～4號與7號梁底數據，并未采集5，6號梁底試驗數據，因此，無法將輕荷載轉變為重荷載得到的校驗系數與傳統荷載計算的校驗系數針對每片梁一一對應比較，故將2種試驗方法得到的校驗系數的分布范圍與平均值做統計對比，結果如表12所示。

由表12可知，試驗橋梁采用傳統荷載試驗方法得到的校驗系數和輕荷載試驗方法計算的校驗系數相比，應變校驗系數平均值誤差分別為1.14%，7.95%；撓度校驗系數平均值誤差均為5.97%，各校驗系數平均值誤差均在10%以內，說明基于影響線輕荷載加載的試驗方法得到的校驗系數相對于傳統試驗得到的校驗系數的誤差較小，可用于橋梁的承載力快速評定。

表12 傳統荷載試驗與輕荷載試驗校驗系數對比

4 結語

利用影響線輕荷載試驗對橋梁進行承載力快速評估，得到以下結論。

1)利用影響線輕荷載對新橋或仍處于線彈性范圍內舊橋承載力進行評估，評估結果和傳統荷載試驗評估結果相比誤差較小，和傳統荷載試驗相比，應變校驗系數和撓度校驗系數的平均值誤差均≤10%， 表明基于影響線的輕荷載試驗方法具有高效性與可行性，可實現橋梁承載力快速評估。

2)輕荷載試驗利用更少的測試車輛完成試驗，且花費較少試驗時間，相比于傳統荷載試驗節省人力物力，降低試驗成本。

3)基于影響線的輕荷載試驗，僅需1輛測試車便可完成荷載加載及試驗數據采集，且準靜力影響線包含更多的橋梁靜力信息，結構響應數據精準可靠，評估結果準確可靠。