基于聯合小波域深度學習的地震數據規則化方法

張 巖 李 杰 王 斌 李新月 董宏麗

(①東北石油大學計算機與信息技術學院，黑龍江大慶 163318；②東北石油大學人工智能能源研究院，黑龍江大慶 163318；③黑龍江省網絡化與智能控制重點實驗室，黑龍江大慶 163318)

0 引言

在理想情況下，地震數據的采樣規則且密集。但是，受復雜地表、地下地質條件、采集因素等的影響，易出現空間采樣不足、地震數據缺失等不規則的問題，影響后續地震資料的處理、解釋結果，因此地震缺失數據的規則化重建非常重要。

從二十世紀八十年代起，學者們就開始研究地震數據規則化重建方法[1]。目前常用的方法大致分為兩類：一類是基于傳統模型；另一類是基于深度學習。

基于傳統模型的地震數據規則化方法主要分為五種，即：①基于相干傾角插值的方法[2-4]，通過掃描時空窗內同相軸的傾角，然后沿著若干個傾角方向通過加權和的形式產生內插的地震道。此類方法處理過程復雜且易受噪聲干擾，難以應用到實際場景中。②基于變換域的方法，利用地震數據在某個變換域的稀疏性進行重建[5-10]，如利用Fourier變換[6]、Con-tourlet變換[7]、Ridgelet變換[8]、Curvelet變換[9]、快速離散曲波變換(Fast Discrete Curvelet Transform，FDCT)算法[10]等，可以較好地進行地震數據規則化。③基于波場延拓算子的方法[11-13]，把缺失道作為零道，結合波動方程部分偏移對疊前地震數據進行重建。該類方法可將傾角時差處理(Dip-Moveout Processing，DMO)與反DMO相結合實現地震數據重建，但在地質信息缺失的情況下，存在重建精度低和運算量大的缺點。④基于濾波器的方法[14-16]，通過褶積插值濾波器實現不規則數據重建，通常把某類插值濾波器應用于待規則化的數據，進行褶積操作。此類方法往往具有較高的計算復雜度。⑤基于壓縮感知(Compressed Sensing，CS)[17-21]的規則化技術，將不規則地震數據作為完整地震數據的少量信號投影值，在處理端通過稀疏性約束正則化方法實現數據的近似重建，從而突破奈奎斯特采樣定理的瓶頸。上述方法共同的問題是所建立的復雜模型通常求解困難，且僅適用于某個特定情況，模型的泛化能力較差。此外，部分模型在缺少地震數據先驗知識(如偏移速度、均方根速度、疊加速度等)的情況下，地震數據規則化處理的質量會受到影響。

近年來，深度學習理論與方法逐漸用于地震數據重建。基本原理是通過學習大量的地震數據樣本，得到目標區塊地震數據分布特征的非線性映射函數，預測相應位置上缺失地震道的實際值，以達到恢復數據中缺失道、規則化地震數據的目的。常見的深度學習重建規則化地震數據的方法包括卷積神經網絡(Convolutional Neural Networks, CNN)、生成對抗神經網絡(Generative Adversarial Networks，GAN)和自編碼器(Auto-Encoder, AE)三類。其中：①基于CNN的規則化方法中，Wang等[22]提出了一種基于ResNets網絡的地震資料插值算法，在網絡層數較深時效果較好，但需要事先對缺失的數據做預插值處理；Wang等[23]提出利用格林函數的空間互易性重建數據，降低了神經網絡在訓練過程中對樣本多樣性的依賴，但同樣需要對網絡輸入的地震數據缺失部分做預插值；高靜懷等[24]通過交替迭代求解地震數據重建的最小二乘法問題和預訓練的網絡模型對地震數據進行重建，同樣需要在迭代初始以及輸入網絡前對缺失數據進行預處理。王鈺清等[25]提出了一種基于數據生成和增廣的CNN，可用于小樣本的網絡訓練。②基于GAN的規則化方法中，Chang等[26]等提出了一種基于GAN的地震數據插值重建技術；Oliveira等[27]利用GAN對疊后地震數據進行重建。這兩種方法均取得了較好的效果，但GAN網絡主要存在的問題是訓練過程不穩定，結果收斂困難。③基于AE的規則化方法中，鄭浩等[28]利用卷積AE，學習完全采樣地震數據與缺失重建數據的映射關系，通過殘差學習預測缺失數據并進行重建輸出，在測試模型上取得了較好的效果；Jia等[29]利用支持向量機重建規則欠采樣的地震數據，需要對網絡模型進行預插值；宋輝等[30]提出了一種基于卷積降噪AE，可以對地震數據以無監督的方式去噪。

上述深度學習規則化地震數據重建方法利用樣本數據時域均方誤差(Mean Square Error，MSE)信息損失作為約束，通過網絡輸出的規則化數據逼近實際完全采樣的地震數據，可以達到較好的信噪比評價結果。Zhu等[31]考慮頻域特征的提取，利用短時Fourier變換將時域的數據轉化到頻域，將實部和虛部傳入CNN，通過逆變換得到時域的重建地震數據。此方法可以在頻域上消除混疊效應，但在能量較弱區域效果不理想。基于深度學習的方法不需要建立復雜的數學模型，相對于傳統的基于模型的方法，它能得到數據深層的特征信息，在缺少地下介質先驗知識的條件下也可以取得較好的效果。但是，目前基于深度學習的方法還存在一些問題：①通常只關注地震數據單一域特征信息的提取，未挖掘數據聯合域的特征信息；②在時域上重建地震數據的方法容易出現細節模糊或過于平滑的現象，丟失紋理信息，影響后續地震數據的解釋；反之，若僅關注頻域的特征信息，在地震數據能量較弱的區域重建的數據質量較差，無法反映實際的數據特征。

小波具有多尺度分析、多方向性的特點，在圖像恢復領域取得了較好的效果。Anbarjafari等[32]提出了利用小波變換將圖像從頻域分解為平滑子圖與細節子圖的方法，并利用細節子圖輔助恢復高質量的圖像；Gao等[33]提出了一種混合小波的卷積網絡，將輸入數據分解成稀疏特征圖譜，然后用另一個卷積網絡進行稀疏編碼、恢復圖像；張巖等[34]考慮其他物理約束信息，提出了一種聯合傅里葉域的去噪CNN，取得了較好的紋理保持效果和較高的信噪比；Wang等[35]引入阻抗域的損失，提出了一種基于閉環CNN測井約束地震反演方法，應用于真實地震數據，獲得了較好的效果。

據此，本文提出基于聯合小波域深度學習的地震數據規則化方法。首先，建立聯合深度CNN學習地震數據在時域與小波域的分布特征，得到規則化數據的預測模型，將不規則地震數據的重建轉化為CNN小波系數的預測；其次，設置結合時域與小波域的損失函數，通過地震數據的整體特征和局部細節信息約束網絡模型，調節聯合損失函數的平衡系數以調整網絡模型學習的注意力。模型測試和實際數據應用均表明，該方法具有很好的細節保持效果，更具魯棒性。

1 方法原理

1.1 不規則地震數據重建模型

假設完整的地震數據為x。實際上，在缺道或稀疏采樣等條件下，采集到的不規則地震數據y可以表示為

y=Rx

(1)

式中R為采樣矩陣，表示從M道地震數據中采樣得到M1道(M>M1)。基于深度學習的地震數據規則化重建過程，就是通過學習樣本特征從y中重建得到完全采樣地震數據的近似估計x′(x′≈x)，利用多次迭代使訓練結果趨于穩定，并逐漸逼近x。

1.2 基于小波變換的地震數據規則化

以樣本x作為時域的標簽。通過濾波器組對x進行二維小波分解，即

(2)

式中：hψ為低通濾波器；hφ為高通濾波器；下標中的“-”表示卷積操作中的翻轉操作；⊕表示卷積運算；j=0,1,2,…,J-1，J為最大尺度因子；m=n=0,1,2,…,2j-1；A、V、H和D分別表示低頻分量、水平高頻分量、垂直高頻分量和對角高頻分量，對應小波域的標簽C=(C1,C2,C3,C4)。

以y作為網絡輸入，利用網絡G訓練得到各頻率分量的小波系數

(3)

式中：GA、GV、GH、GD分別為低頻分量、水平高頻分量、垂直高頻分量、對角高頻分量對應的映射；A′、V′、H′、D′分別表示為網絡訓練所得小波系數不同方向低頻分量、水平高頻分量、垂直高頻分量、對角高頻分量，對應網絡訓練的預測小波系數C′=(C′1,C′2,C′3,C′4)。

小波反變換后得到重建時域數據x′。聯合計算時域與小波域的誤差，設置全局損失函數ltotal作為約束，并通過正向傳遞和反向傳播調整網絡參數。經過多次迭代，網絡訓練結果趨于穩定，得到最終網絡模型，將地震數據規則化問題轉化為小波系數預測問題。

損失函數采用在數據采樣點處x與x′的均方誤差，即

(4)

1.3 小波域特征提取

地震數據的波前信息在時域上表現為復雜的紋理狀曲線，盡管多層CNN具有較強的特征提取能力，但僅利用時域信息提取特征時具有很大的局限性。小波變換通過縮、放母小波的寬度獲取信號的頻率特征，平移小波基獲取信號的時間信息[36]。信號的小波變換相當于利用母小波的縮、放和小波基的平移，并與原始信號卷積，得到小波系數(圖1)。

圖1 小波變換示意圖

選擇haar小波作為小波基，根據二維快速小波變換(Fast Wavelet Transform，FWT)[37]計算haar小波系數，圖2為地震數據進行小波分解的實例。由小波變換的系數分布特性可知，低頻小波系數的預測可以保留地震數據全局的主要特征信息，高頻小波系數的預測有利于地震數據細節的恢復。

圖2 時域(a)與小波域(b)地震數據對比

為了充分利用小波域的特征，本文設計了小波預測損失和紋理損失兩種損失函數。前者是小波域均方誤差的加權形式，定義為

(5)

式中：λk是平衡不同小波子帶重要性的權重系數；n為小波系數分量數。賦予高頻系數較大的權重，可以將訓練注意力集中在局部高頻細節重建上，生成細節效果較好的規則化地震數據。為了防止過擬合導致高頻小波系數收斂到0，定義紋理損失為

(6)

式中：q為約束高頻小波系數的初始子帶序號，本文采用一級小波分解，生成的低頻分量子帶保留數據主要信息分量，其余三個子帶為不同方向的高頻分量；γk、α和ε均為平衡系數，其中γk為各高頻分量的權重，α略大于1，ε略大于0。ε保證了ltexture不為0，從而使高頻小波系數非零，防止小波高頻系數訓練過擬合。

1.4 聯合小波域深度學習網絡設計

本文設計的聯合學習CNN模型G如圖3 所示，由嵌入層網絡、小波系數預測網絡和聯合損失計算3個子網組成。

圖3 網絡模型結構

1.4.1 嵌入層網絡

不規則的地震數據輸入嵌入層網絡后，經過多層卷積特征提取，將得到的特征圖譜傳遞給后續網絡。輸入的不規則地震數據尺寸為128×128，嵌入層網絡的所有卷積核尺寸均為3×3，步長為1。通過補“0”操作使特征圖譜尺寸與輸入數據相同。卷積后的特征圖譜經過歸一化和激活函數，再進入下一層操作。卷積層、歸一化層和激活函數構成一個殘差塊，前、后殘差塊之間設置殘差連接，可以加速收斂和防止梯度消失。每層卷積核的數量沿前向遞增，分別是128、256、512、1024，為小波系數預測網絡提供足夠的特征信息。

1.4.2 小波系數預測網絡

小波系數預測網絡由4個獨立的并行子網絡組成，它利用嵌入層網絡提取的特征圖譜學習、預測不同頻率分量的小波系數。地震數據具有較強的曲線紋理特征。以一級小波分解為例，將小波預測網絡分成4個獨立的小波預測子網絡；再通過CNN單獨處理對應方向子帶的小波系數，重建規則化的地震數據。每層網絡的卷積核的尺寸為3×3，步長為1，網絡預測的小波系數尺寸與不規則地震數據輸入的尺寸相同。由于每個子網預測的小波系數相對獨立，因此網絡更具魯棒性。

1.4.3 聯合損失計算

聯合損失計算是對地震數據小波域和時域的損失進行評價。網絡將各個獨立小波預測子網的小波系數反變換為時域的規則化地震數據，使其與完全采樣的地震數據進行對比、計算損失，再反向傳遞到網絡中，從而更新網絡參數權重。

1.5 聯合損失函數

網絡的聯合損失函數由三部分組成，即全局信息預測損失、小波系數預測損失和紋理細節預測損失。其中，全局信息損失是計算重建的時域規則化地震數據與完全采樣地震數據之間的損失，以均方誤差作為約束條件；小波系數預測損失是利用完全采樣地震數據的小波系數對預測子網得到的小波系數施加約束；紋理細節預測損失是計算輸入數據與標簽之間小波變換高頻分量的誤差，加強此部分的約束可改善地震數據規則化的紋理細節效果。

設空間域的均方誤差為全局損失lfull，聯合誤差函數為

ltotal=lwavelet+μltexture+νlfull

(7)

式中μ和ν是平衡參數，可根據網絡訓練目標的側重點進行調整，以改變網絡學習的注意力。

由于小波系數與不規則的地震數據輸入尺寸相同，因此通過CNN可使每個特征圖譜的大小保持一致，可以降低訓練難度、兼顧地震數據的全局拓撲信息和紋理細節信息。

2 模型測試

2.1 參數設置

選擇Marmousi模型測試本文方法。震源和檢波器置于地表，通過中間放炮、兩端接收的方式進行正演獲取地震道集數據，檢波器采樣間隔為4ms，道間距為10m。完全采樣實驗樣本數據裁剪尺寸為128×128的切片數據x，作為訓練樣本時域標簽。從完整地震數據抽取比例為r的地震道作為不規則的地震數據樣本，其他道為空道，分別以隨機抽取和均勻抽取的方式仿真稀疏采樣兩種不規則情況。

地震數據重建效果的衡量指標采用信噪比(Signal-to-Noise Ratio，SNR)

(8)

式中N表示樣本數量。

將10000組Marmousi模型數據按照8∶1∶1比例且不交疊的方式分別劃分為訓練集、驗證集和測試集。在訓練階段，使用訓練集數據進行訓練并用驗證集評估網絡訓練效果；當驗證集結果趨近收斂時保存網絡模型和參數，并用測試集數據對預訓練模型進行評估。

2.2 網絡模型測試

針對均勻采樣和隨機采樣兩類情況，制作從10%～90%共9組不同采樣率下的樣本(每組采樣率間隔為10%，兩類采樣樣本共18組)，分批次輸入網絡進行訓練。不同采樣率下訓練的不同網絡模型用來測試相應采樣率下的地震數據。

由圖4可見，在不同采樣率條件下，本文方法(聯合小波域的深度學習方法)均較好地保留了實際地震數據的特征；隨著采樣率不斷提高，規則化效果也隨之提升。

圖4 不同采樣率條件下均勻采樣數據(上)及其規則化重建結果(下)

圖5為本文方法在驗證集測試的評估結果。由圖5a可見，隨著迭代次數增多，SNR逐步提高，重建效果不斷增強；當達到1000次時，算法取得收斂，SNR基本穩定在最大值附近，說明本網絡模型具有較好的收斂性和穩定性。為了使網絡更好地收斂至最優解，防止訓練后期學習率過大，本文采用指數衰減算法，設置初始學習率為2×10-4，每次迭代衰減指數為0.995(圖5b)。迭代初期用較大的學習率使結果快速收斂，所以前期聯合誤差數值變化相對較為劇烈(圖5c)，有助于加速重建地震數據；后期減小學習率，使目標函數收斂至局部最小值，聯合誤差變化相對緩慢(圖5c)，有利于重建規則數據細節信息。另外，在訓練過程中網絡調整參數導致結果振蕩，但是網絡會根據損失函數進行調整，從而使最終結果趨于穩定。

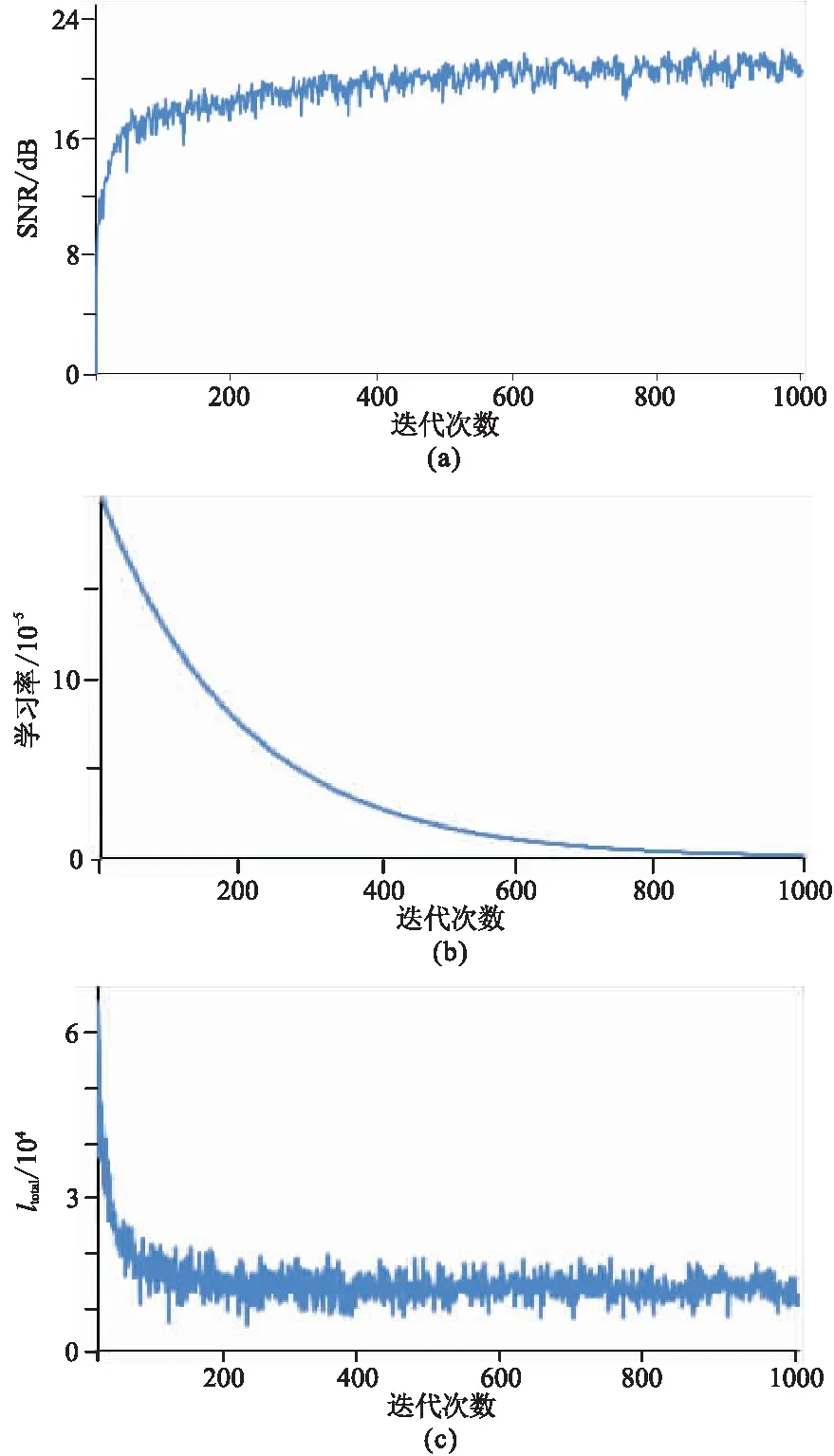
圖5 SNR(a)、學習率(b)和ltotal(c)隨迭代次數變化趨勢

2.3 紋理細節保持效果

為了驗證本文方法對細節重建的有效性，測試樣本在50%均勻采樣條件下，對比聯合小波域學習網絡(SNR=19.8550dB)和僅使用時域學習網絡(SNR=17.2667dB)的結果(圖6)。由圖可見，聯合小波域學習的網絡局部細節特征更準確，更接近于真實地震數據。這證明了聯合小波變換的CNN具有更好的紋理保持性能。

圖6 50%均勻采樣條件下全采樣(a)與未采用聯合小波(b)、采用聯合小波(c)的重建波形(上)及其局部(紅框)放大(下)

2.4 算法對比測試

將本文方法應用于地震數據隨機缺失的情況，并與當前較先進的重建算法進行對比(圖7)。由圖可見，本文方法重建的地震數據波形連續性好、無突變，更逼近真實地震數據。

圖7 全采樣數據與50%隨機采樣條件下不同算法重建結果對比

本文方法是從全局拓撲信息中預測小波系數，因此在低采樣率情況下具有一定的優勢。由圖8可見，在20%的低采樣條件下，空道占據大部分，很難重建地震數據，因此基于物理建模重建的地震數據均出現大幅度缺失或失真；數據驅動方法重建地震數據整體效果得到大幅提升，但與真實數據相比仍存在細節缺失或重建精度不夠的問題；在較低采樣率(≤20%)且未考慮采樣數據位置的情況下，本文方法重建的地震數據較好地保留了原始地震數據特征和波形信息，在細節處更逼近實際數據。這證明了本文方法對地震數據缺失位置不敏感，在地震數據規則化的過程具有魯棒性。

圖8 全采樣數據與20%均勻采樣條件下不同算法重建結果對比

表1和表2分別對比了均勻采樣與隨機采樣兩種方式不同采樣率條件下本文方法與其他方法測試集樣本數據重建時SNR的均值對比。由表可見，本文方法顯著優于基于模型的規則化方法，也優于同類基于深度學習的規則化方法。對于本文方法而言，在高采樣率(>80%)時，無論是均勻采樣還是隨機采樣，數據整體結構的特征均保持較完整，重建的數據效果比較接近；在中等采樣率(20%～80%)時，均勻采樣比隨機采樣能更好地保留數據的結構特性，均勻采樣重建的效果要優于隨機采樣；在低采樣率(≤20%)時，均勻采樣和隨機采樣嚴重破壞了實際地震數據的結構特性，兩種方法重建效果均較差。

表1 均勻采樣條件下不同方法重建地震數據的SNR均值對比 dB

表2 隨機采樣條件下不同方法重建地震數據的SNR均值對比 dB

在50%隨機采樣條件下，比較不同深度學習方法訓練效率。不同方法訓練迭代1000次的訓練完成時間如表3所示。由表可見，聯合小波學習方法相比于時域學習方法增加了計算時間，但增加幅度相對較小，重建地震數據SNR卻得到了較大程度地提高。

表3 不同深度學習方法訓練所用時長及重建地震數據的SNR均值對比

3 實際地震數據測試

選取A油田實際地震數據測試本文方法規則化處理效果。震源和檢波器置于地表，檢波器采樣間隔為2ms，道間距為12.5m。將實際樣本數據共5000個按照8∶1∶1分別劃分為訓練集、驗證集和測試集，使用訓練集數據訓練網絡，再用測試集測試網絡的有效性。任選1個測試集樣本，實際地震數據不同方法重建波形對比如圖9所示。由圖可見，本文方法重建的地震數據同相軸光滑、連續，可較好地重建缺失道和細節，具有較好的魯棒性。

圖9 實際地震數據及不同方法重建波形對比

為了驗證本文網絡的泛化能力，將B采油廠疊前和疊后地震數據各抽取5000組樣本，制成一個樣本增廣的地震數據集，訓練集、驗證集和測試集按不交疊的方式劃分比例為8∶1∶1，通過結合兩種樣本數據集進行網絡訓練。當訓練收斂時，分別使用測試集中疊前和疊后數據分別進行測試。當測試數據為疊前數據時，規則化地震數據SNR=16.0539dB；當測試數據為疊后數據時，規則化地震數據SNR=16.331dB。這表明本文網絡具有一定的泛化能力和適用性。

4 結束語

本文提出的聯合小波域深度學習的地震數據規則化方法有效利用了頻域和時域的特征。對比基于模型的方法以及僅在時域學習條件下的重建效果，本文方法具有細節保持效果好、對地震數據缺失位置不敏感、在采樣率較低的情況下具較好的重建效果的特點。實際地震數據重建結果驗證了本文方法的準確性和有效性。需要指出的是，基于卷積神經網絡的方法往往需要大量數據學習相應地震數據的特征，所以如何僅在有限量樣本的情況下，提高模型的泛化能力，取得相對理想的效果，是進一步研究的方向。