基于Hilbert包絡與階次分析的軸承故障診斷
王益有,胡勇峰,王亞杰,史俊旭
株洲中車時代電氣股份有限公司,湖南株洲 412001
0 引言
新能源汽車在異響故障診斷過程中,由于異響故障的特性隨車速(電機轉速)變化而變化,診斷時需要對汽車的加速或減速過程進行監測,收集全面的故障信息,進行快速識別故障,確定問題根源。由于測試是在電機變轉速的工況下進行,其振動信號為非平穩信號,如果采用傳統的譜分析技術,會產生頻譜分量重疊現象。階次分析是一種分析旋轉或往復機械噪聲與振動信號的技術,適應于分析轉速隨時間變化的噪聲與振動信號。
軸承是汽車動力系統中的重要零件,它的運行狀態是否正常直接影響到整個汽車動力系統的性能。軸承故障也是新能源汽車異響的重要來源之一,其故障診斷中頻域特征提取方法主要有頻譜分析、功率譜分析、倒譜分析、細化譜分析、AR模型譜分析、高階譜分析和包絡譜分析等。其中包絡分析方法將與故障有關的信號從高頻調制信號中取出,避免了其他低頻信號的混淆,具有極高診斷可靠性和靈敏度,在滾動軸承故障特征提取中應用較為廣泛。
本文以Hilbert包絡和階次分析為基礎,結合新能源汽車異響故障的特點,提出基于Hilbert包絡與階次分析的調制階次提取,并與軸承故障特征相結合的故障診斷方法。通過某汽車異響問題的測試與分析,闡述了利用該方法進行故障診斷的實現過程。結果表明,利用提出的方法進行汽車加速工況下的異響故障診斷是可行的。
1 Hilbert包絡提取
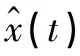
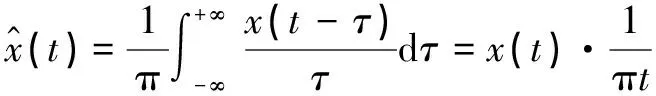
(1)
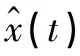
()=()cos[2π+()]
(2)
式中:()為幅值調制信息;()為相位調制信息;為載波頻率。
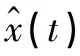
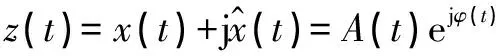
(3)
其中幅值()為:
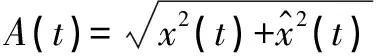
(4)
其中相位()為

(5)
信號的()即為()的Hilbert包絡。
由以上分析可知,Hilbert變換是將時域信號變為時域解析信號的方法。變換所得到的解析信號的實部是實信號本身,虛部是實信號的Hilbert變換,解析信號的幅值即為實信號的Hilbert包絡。
對包絡進行頻譜分析,可以得到包絡信號的包絡譜,Hilbert包絡具有解調功能,能分離出信號的低頻信息進行解調,因此,由包絡分析得到的結果往往比較清晰直觀。
2 階次分析介紹
頻譜分析是軸承故障診斷和故障檢測的常用方法,但該方法不僅需要知道軸承的內部幾何結構參數,還需要知道機械的旋轉轉速等信息,且只適用于穩態信號的分析處理。頻譜分析提取頻率響應不僅包括軸承故障頻譜特征頻率及諧頻,還包含旋轉機械其他部件激發出來的頻率成分,從而很難直接識別。
在汽車的振動數據采集時,車速隨著路況的變化很難實現穩定的車速,從而無法進行穩態的故障信號收集,采用傳統的頻譜分析方法時,會產生能量分散現象。階次分析方法源于角度域采樣理論,其通過同步采集旋轉機械的轉速,進行等角度增量重采樣得到角度域內的振動響應信號,則時域非穩態信號在角度域下是穩態信號,在對角度域穩態信號進行傅里葉變換就可以得到清晰的階次譜。屬于階次分析方法剔除了機械運轉的影響,是一種有效的非穩態信號分析方法,適用于變轉速工況下的數據分析。
為了確定等角度采樣的時間點,通常先需要設定參考軸的轉速模式,假定在一個很小的同步采樣時間間隔Δ范圍內參考軸為勻角加速度運動,則數值積分后參考軸的轉角可表示為
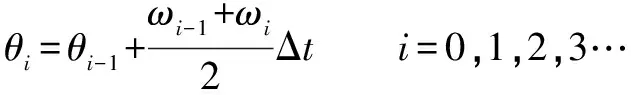
(6)
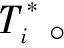
3 軸承故障特征
磨損是軸承最常見的故障。潤滑不良、軸承超載、異物進入、安裝不良、銹蝕等原因通常會引起工作表面疲勞剝落、壓痕、銹蝕、膠合、斷裂等離散型缺陷或局部損傷,統稱為表面損傷類故障。
當軸承的內圈、外圈、滾動體出現點蝕等損傷故障時,其運轉時就一定會產生相應的頻率沖擊。根據軸承產生缺陷的零部件位置不同,滾動軸承的缺陷階次特征計算公式如下。
內圈滾道缺陷:
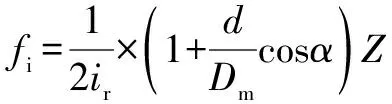
(7)
外圈滾道缺陷:
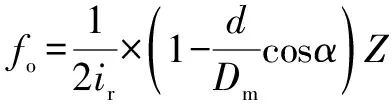
(8)
滾珠缺陷:
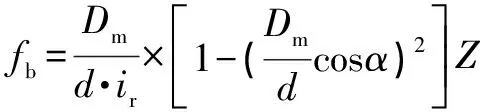
(9)
保持架缺陷:
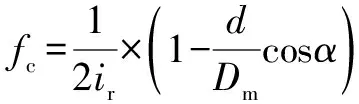
(10)
式中:為滾動體數目;為滾動體直徑;為節圓直徑;為軸承的壓力角;為輸入軸與軸承中間的傳動比。
基于Hilbert包絡與階次的軸承故障診斷流程如圖1所示。
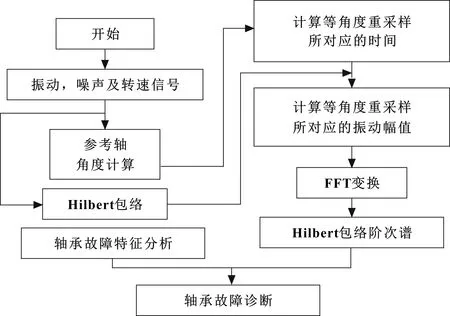
圖1 基于Hilbert包絡與階次的軸承故障診斷流程
4 應用實例
終端客戶反饋某新能源汽車在行駛過程中存在“嗡嗡”異響,主觀感受汽車在中高速行駛時更加明顯。通過汽車在平整的瀝青路面進行加速試驗,同步采集汽車的電機及相應測點的振動噪聲信號。圖2為現場采集得到的電機轉速信號,圖3為車內噪聲原始信號,圖4與圖5分別為動力總成懸置主動側與被動側的原始振動信號。
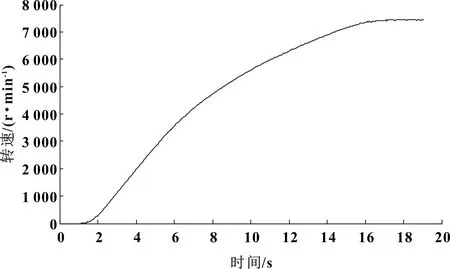
圖2 電機轉速信號
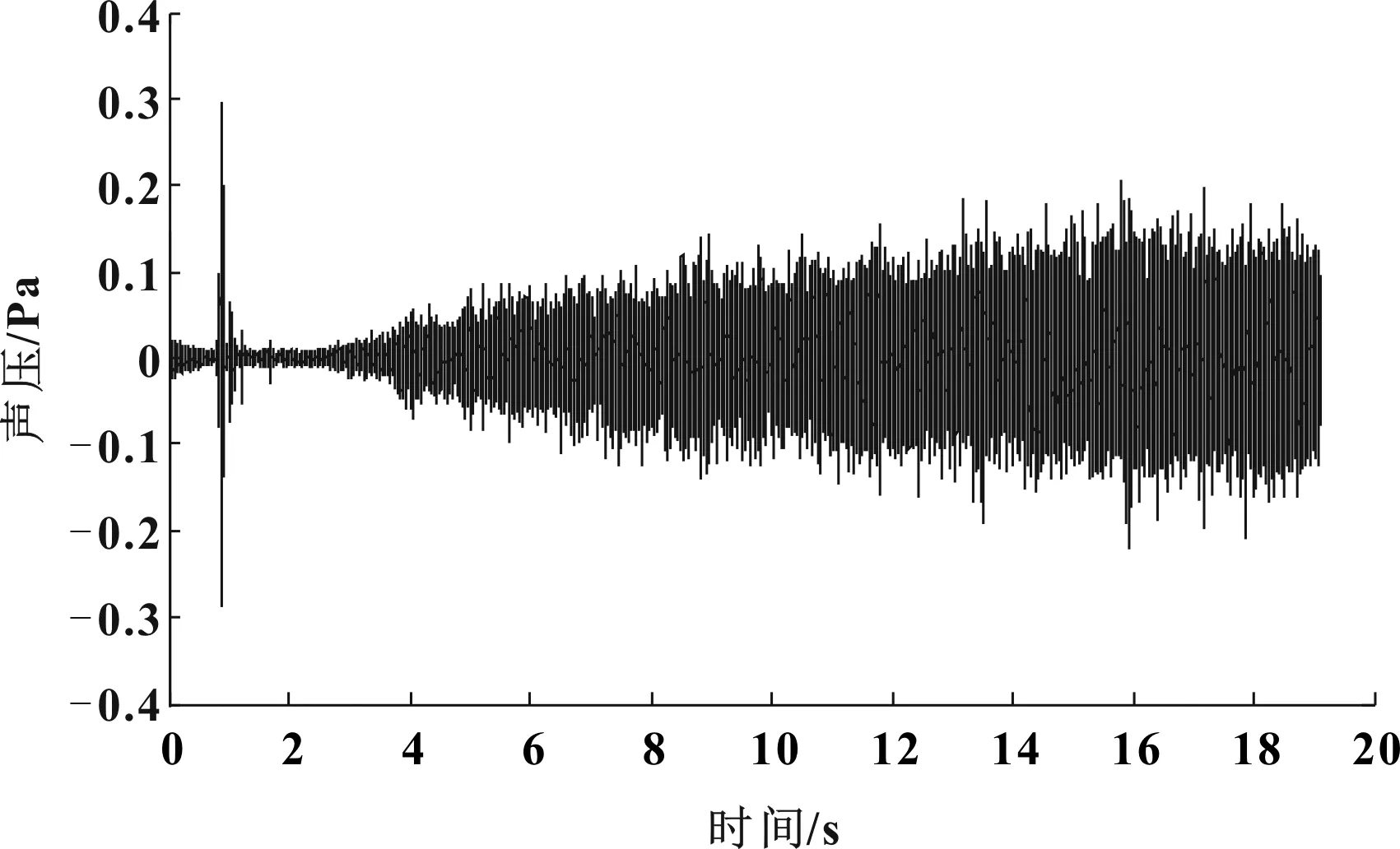
圖3 車內噪聲原始信號
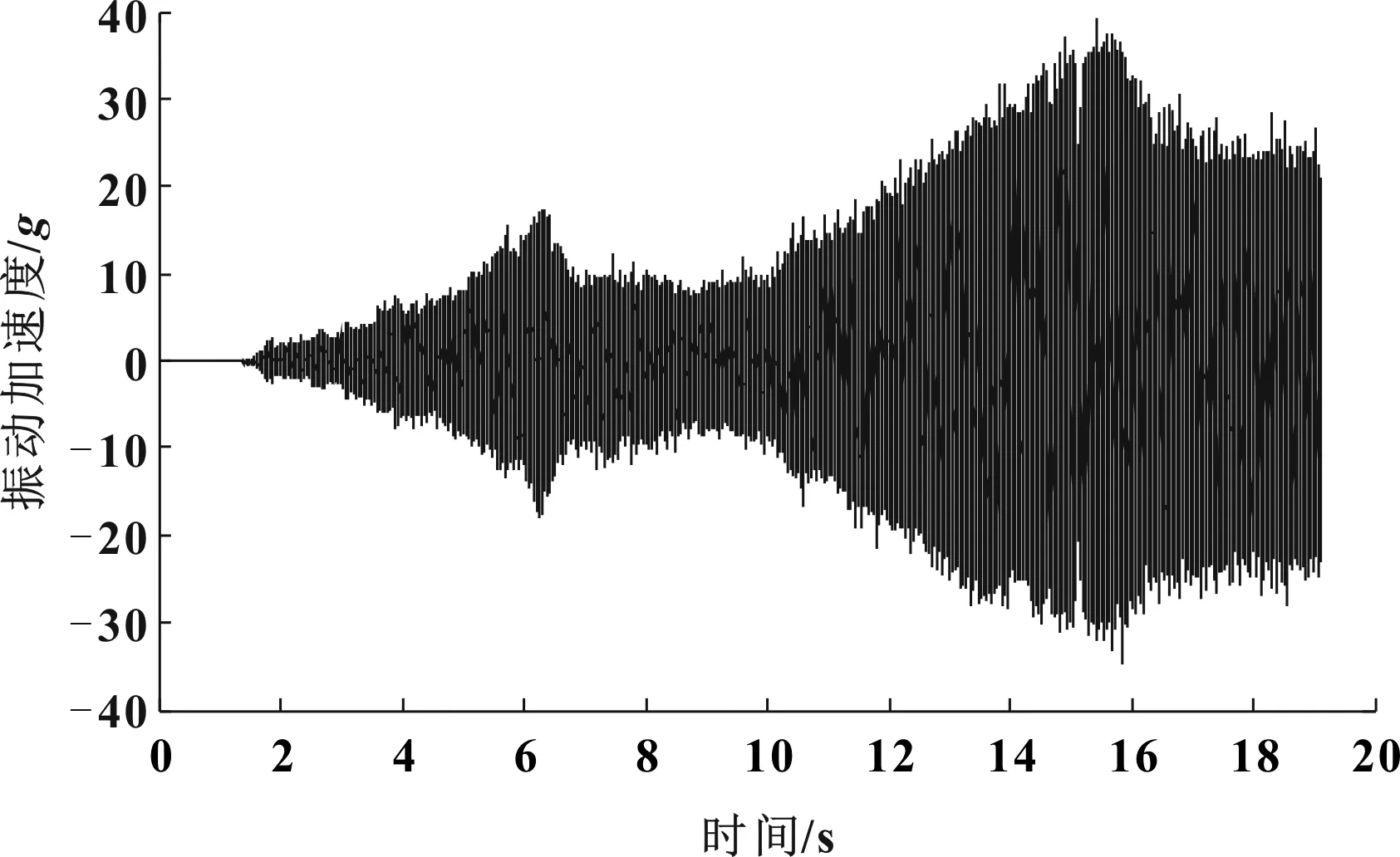
圖4 動力總成懸置主動側的原始振動信號
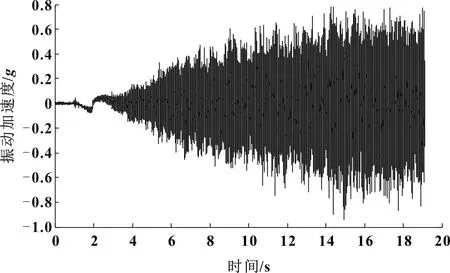
圖5 動力總成懸置被動側的原始振動信號
根據Hilbert包絡原理得到圖6所示的車內噪聲Hilbert包絡曲線如圖6所示,動力總成懸置主動側與被動側的Hilbert包絡曲線如圖7和圖8所示。
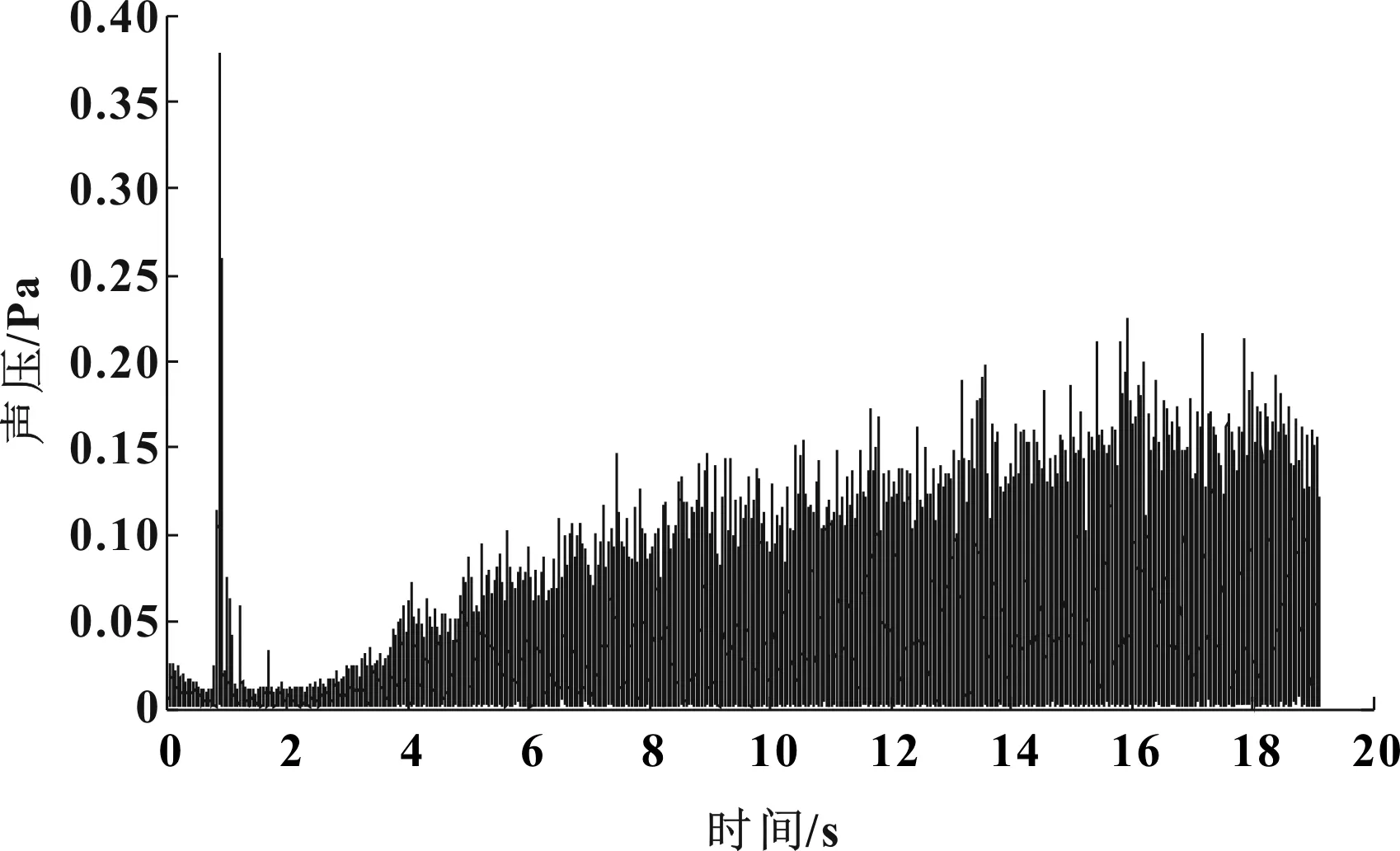
圖6 車內噪聲Hilbert包絡曲線
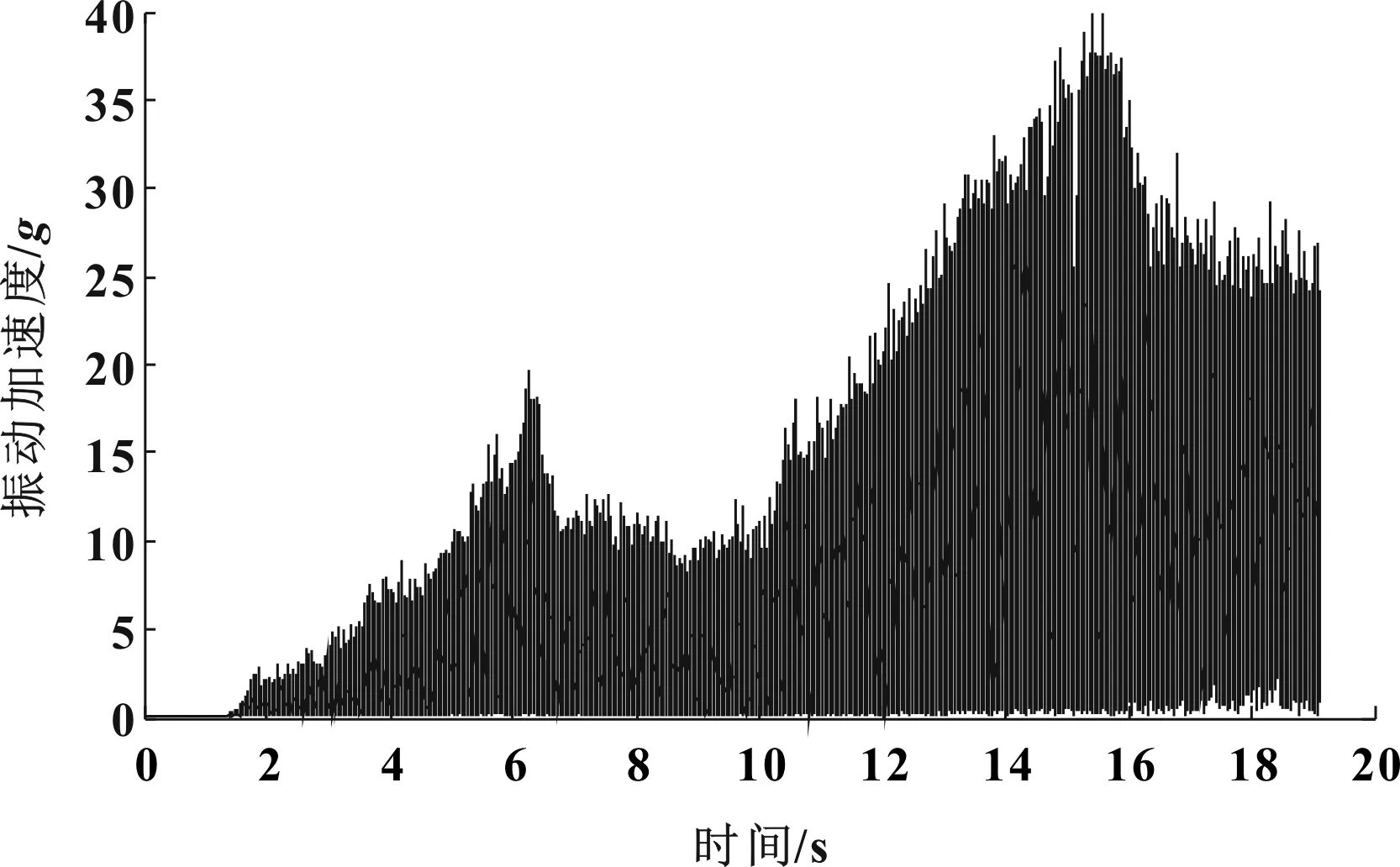
圖7 動力總成懸置主動側的Hilbert包絡曲線
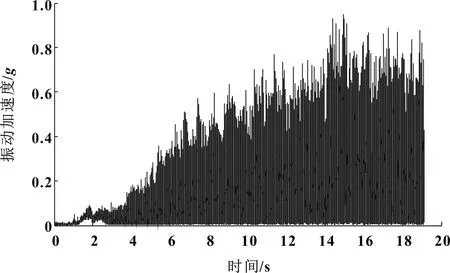
圖8 動力總成懸置被動側的Hilbert包絡曲線
根據公式(1)可計算得到電機旋轉軸的角度曲線如圖9所示。
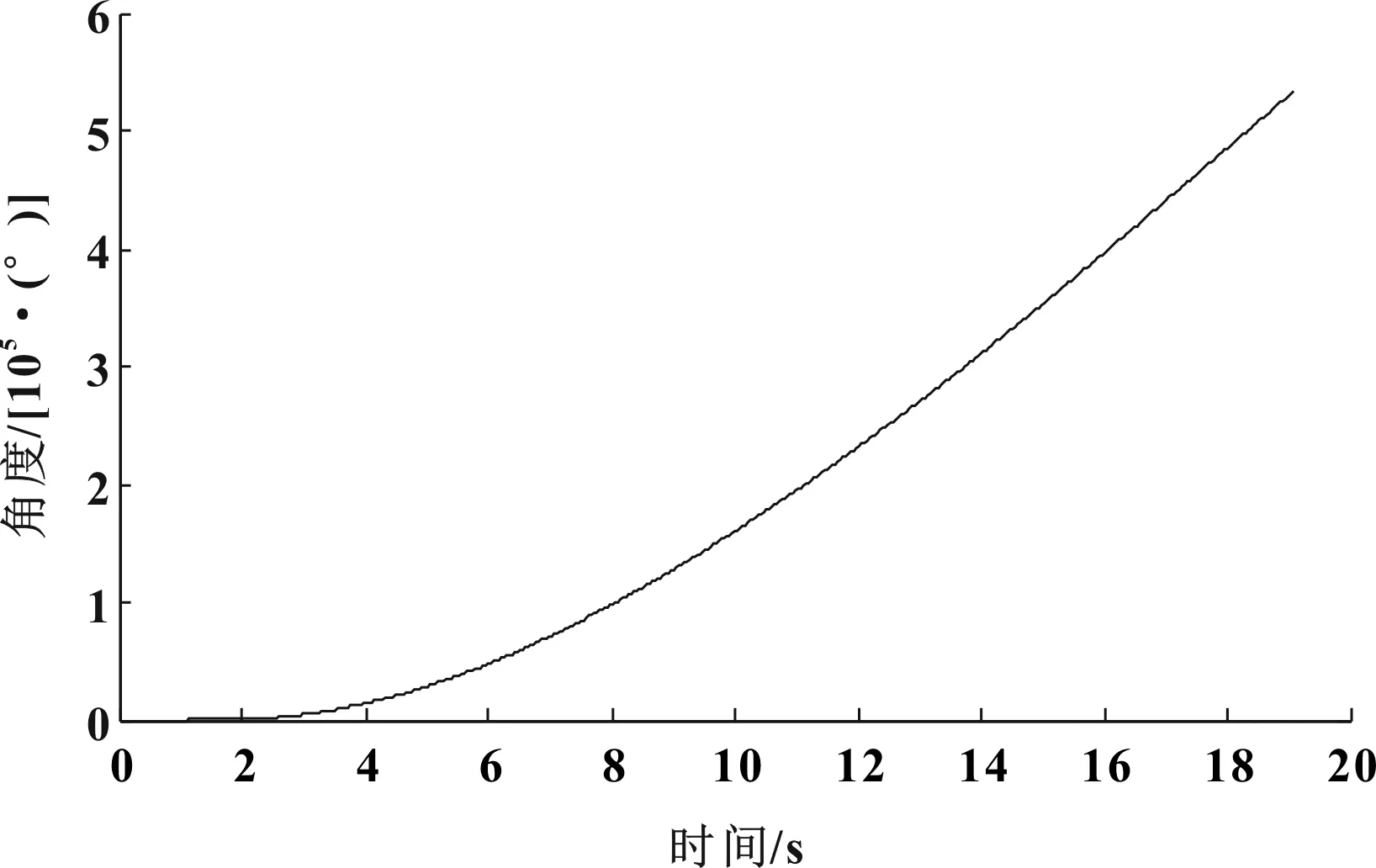
圖9 電機旋轉軸的角度曲線
利用插值算法對圖9中的角度進行等角度間隔插值,可計算得到等角度重采樣的時間,再利用插值算法對圖6至圖8中的包絡幅值進行時間插值可以得到車內噪聲Hilbert包絡角度重采樣曲線如圖10所示,動力總成懸置主動側和被動側Hilbert包絡角度重采樣曲線分別如圖11和圖12所示。
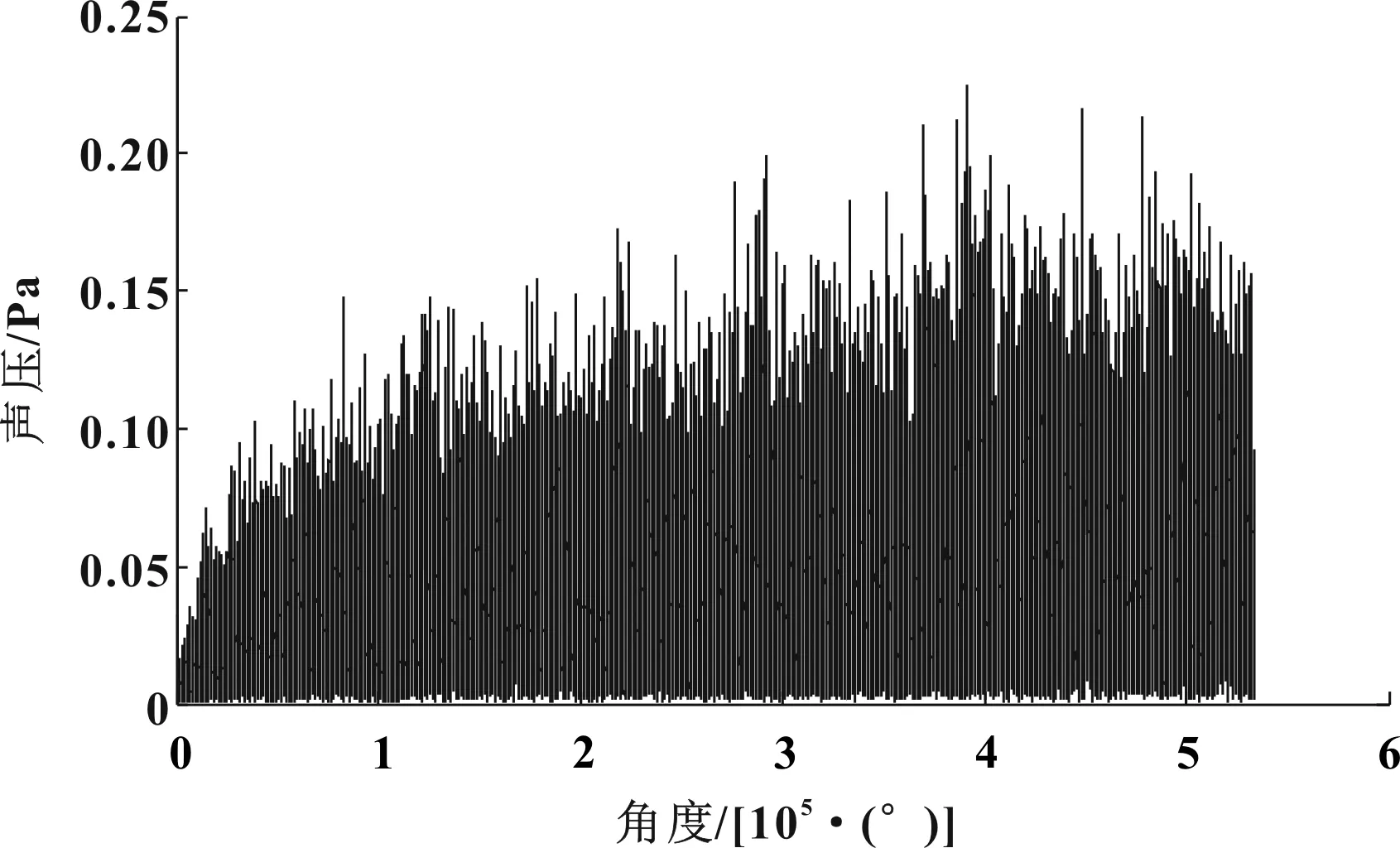
圖10 車內噪聲Hilbert包絡角度重采樣曲線
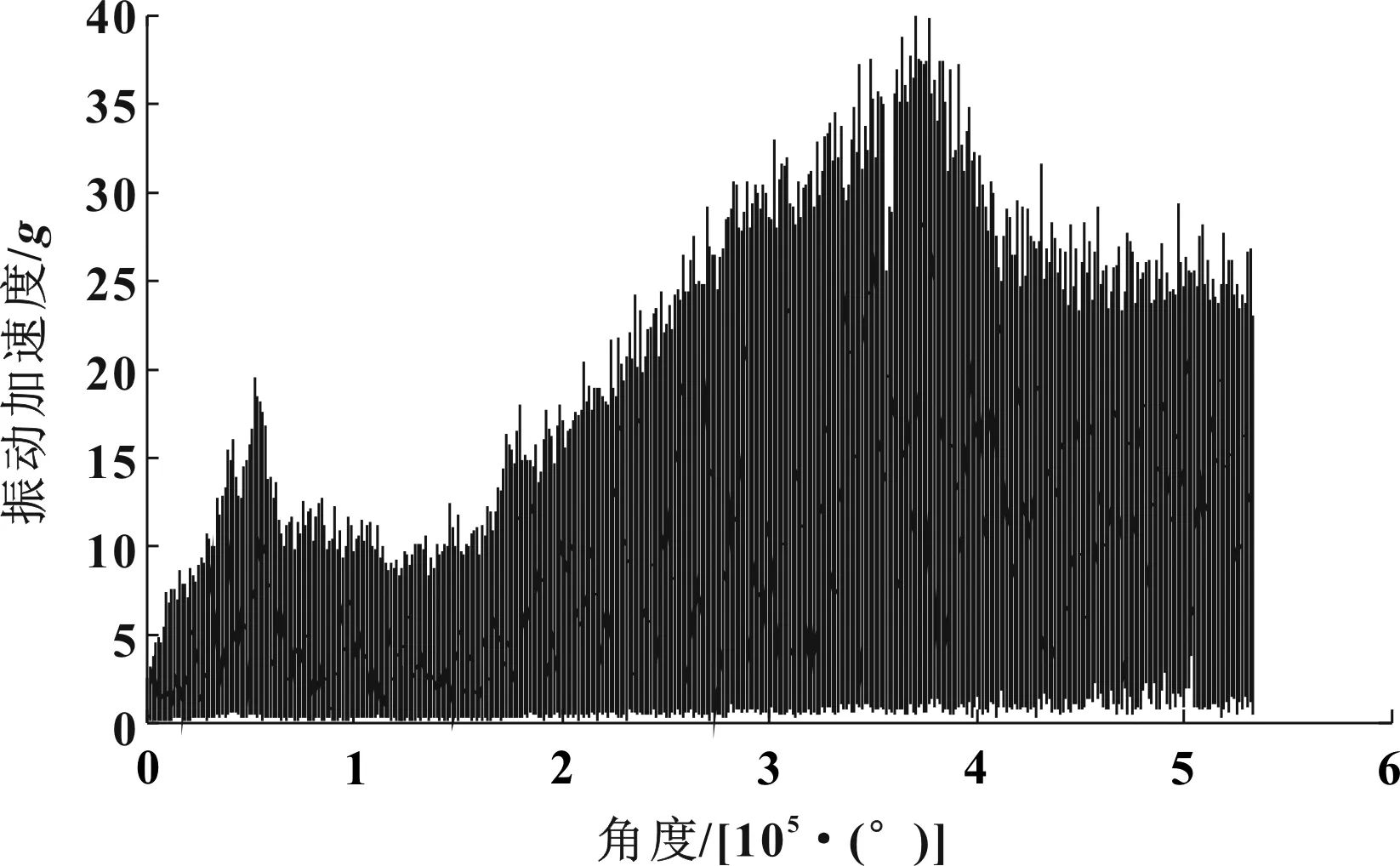
圖11 動力總成懸置主動側Hilbert包絡角度重采樣曲線
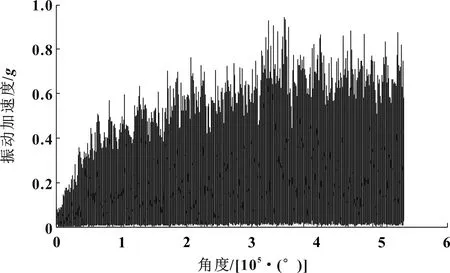
圖12 動力總成懸置被動側Hilbert包絡角度重采樣曲線
對圖10至圖12中的包絡幅值進行FFT變換,得到車內噪聲Hilbert包絡階次譜如圖13所示,動力總成懸置主動側Hilbert包絡階次譜如圖14所示,動力總成懸置被動側Hilbert包絡階次譜如圖15所示。
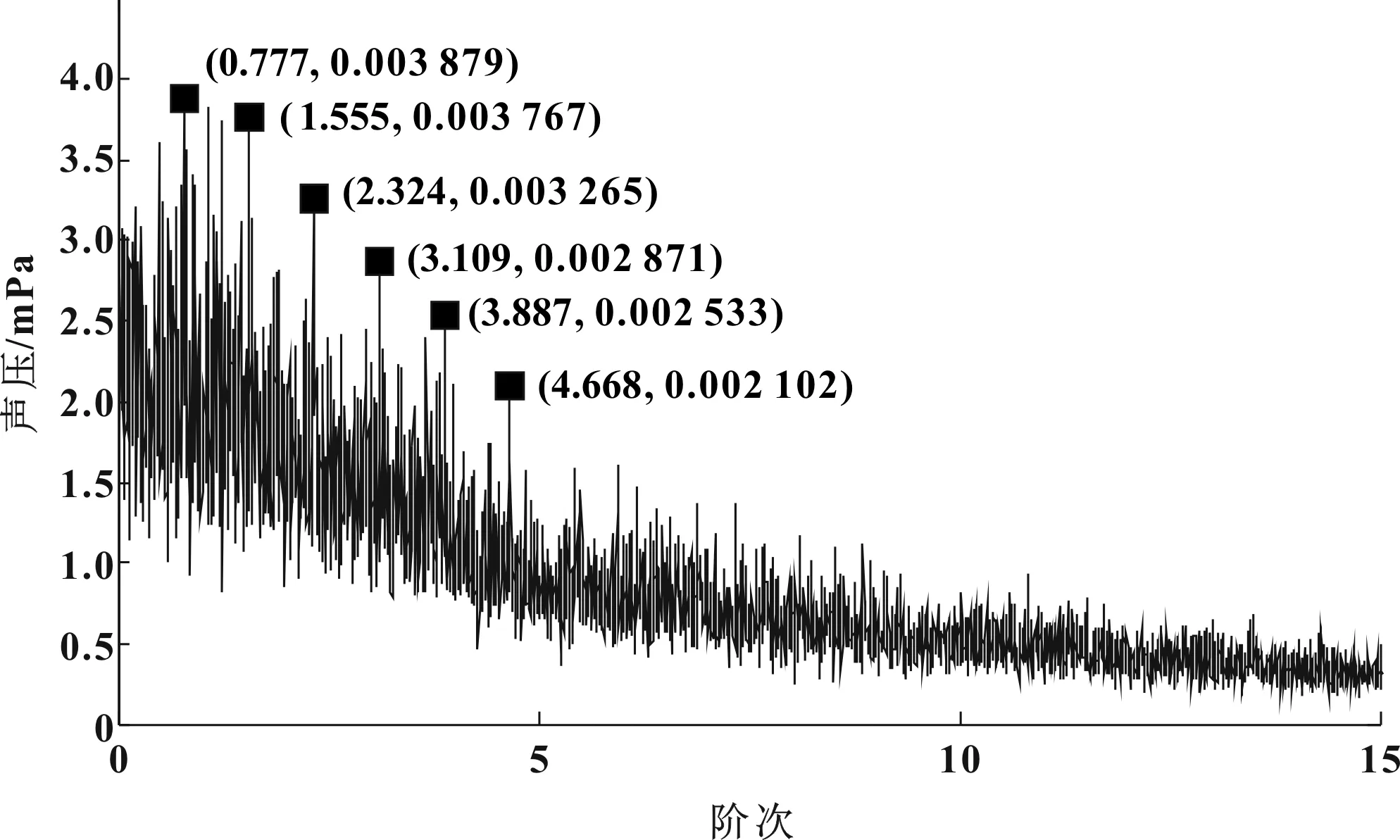
圖13 車內噪聲Hilbert包絡階次譜
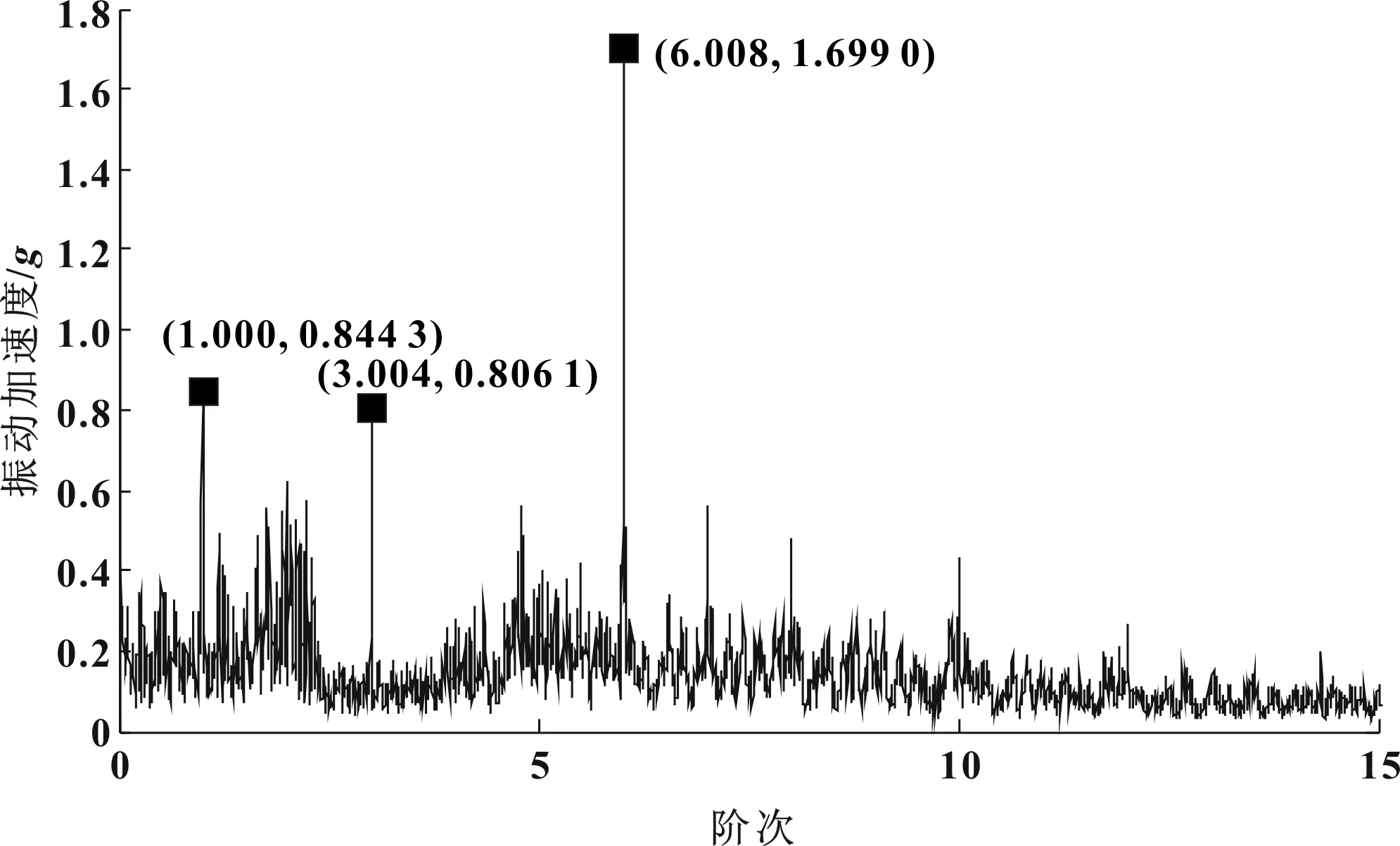
圖14 動力總成懸置主動側Hilbert包絡階次譜
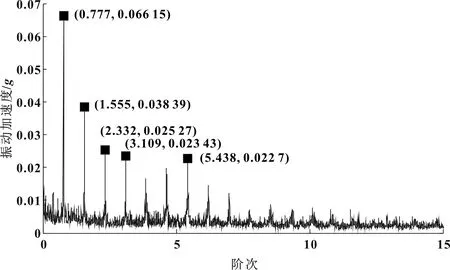
圖15 動力總成懸置被動側Hilbert包絡階次譜
由圖13中的車內噪聲Hilbert包絡階次譜上可以明顯看到0.777階及其倍頻階次,說明車內噪聲存在明顯的0.777階調制,結合主觀感受,可以確認車內“嗡嗡”異響為0.777階調制聲導致的。
由圖14中的懸置主動側振動Hilbert包絡階次譜上可明顯看到1階、3階及6階調制,但0.777階及其倍頻階次不明顯。該特征與車內噪聲特征不同,故車內噪聲與懸置主動側振動相關不明顯。
由圖15中的懸置被動側振動Hilbert包絡階次譜上可明顯看到0.777階及其倍頻階次,說明該振動信號存在明顯的0.777階調制,其特征與車內噪聲特征一致,故車內噪聲與懸置被動側振動相關明顯。
由傳動系統上各軸承參數及轉速比參照公式可計算出軸承參考電機轉速的故障特征階次,該新能源汽車的前輪轂軸承故障特征階次見表1。由表可知,前輪轂軸承的內圈故障特征階次為0.777與車內噪聲及懸置被動側振動的調制階次吻合,故整車的異響是前輪轂軸承內圈故障導致的。該車的前輪轂軸承更換后,車內“嗡嗡”異響消失。

表1 前輪轂軸承故障特征階次
5 結束語
Hilbert包絡能從振動調制信號中有效提取滾動軸承周期性故障沖擊信號。階次分析剔除了運轉變化的影響,是一種有效的非穩態信號分析方法,適用于變轉速工況下的數據分析。利用所提出的基于Hilbert包絡與階次分析的故障診斷方法對異響問題汽車在加速工況下的振動噪聲數據進行分析,并結合傳動系上的各軸承故障特征階次確定故障原因,證明了利用提出的方法進行汽車加速工況下的異響故障診斷是可行的。

