α+β兩相區壓縮變形后TC21合金的顯微組織模擬

余新平，潘光永，黃慶華，潘巧玉

(浙江廣廈建設職業技術大學智能制造學院，東陽 322100)

0 引 言

TC21合金以其低密度、高強度和高韌性等特點在航空航天領域得到廣泛的應用[1-2]，該合金與美國的Ti-62222S[3]鈦合金相當，主要用于新一代軍用飛機重要零部件的制造。

TC21合金的主要變形加工方式為熱鍛，熱鍛可以細化其晶粒，是提高鈦合金性能的有效途徑[4]。鈦合金在不同相區(α+β、近β、準β)的熱鍛過程會由于變形溫度、應變速率、應力等參量的變化，而使其發生的動態回復、動態再結晶等行為也有所不同，從而使合金鍛件最終得到不同的顯微組織，表現出不同的力學性能[5]。熱變形過程的溫度、應變速率和應力等參數間的關系可以用本構數學模型進行描述，從而可定量表征熱變形過程中因動態再結晶等導致的顯微組織演變行為。針對TC21合金有很多學者進行了相關研究，朱知壽等[6]基于熱壓縮試驗分析了退火態TC21合金β相區的動態再結晶組織特征，并建立了流變應力本構數學模型；馮菲等[7]建立了鑄態TC21合金在β單相區的流變應力本構數學模型；余新平等[8]研究了軋制態TC21合金β相區鍛造熱變形過程動態再結晶晶粒尺寸預測模型。然而，針對TC21合金在α+β兩相區動態再結晶行為的研究尚少見報道。基于此，作者針對軋制態TC21合金，進行了α+β兩相區熱壓縮變形試驗，分析了不同熱壓縮變形條件下的顯微組織特征，并建立了流變應力本構及動態再結晶位錯密度模型，最后進行了動態再結晶模擬，以期為相關熱加工工藝的制定提供參考。

1 試樣制備與試驗方法

試驗材料為某航空鍛鑄公司所提供的軋制態TC21合金，其化學成分如表1所示，其α→β相變點為958.1 ℃。其軋制態的顯微組織如圖1所示，主要由等軸的初生α(白色)及β相組成，平均晶粒尺寸為20 μm。

表1 TC21合金化學成分

圖1 軋制態TC21合金的顯微組織

將試驗材料用線切割機加工成尺寸為φ8 mm×12 mm的試樣，并用砂紙將兩端磨平保證光滑無裂紋，然后采用Gleeble-3500型熱模擬試驗機進行熱壓縮試驗，試驗過程中采用二硫化鉬作為潤滑劑。首先將試樣以10 ℃·s-1的速率分別加熱到870，900，930,960 ℃后保溫3 min，使試樣內部溫度均勻;然后進行壓縮，變形量為60%，應變速率分別為0.001，0.01，0.1，1 s-1;試驗結束后迅速將其水冷，以保留其組織狀態。采用線切割機將熱壓縮后的扁平試樣切成兩半，取其中一半用XQ-2B型金相試樣鑲嵌機進行鑲嵌，對試樣端面進行打磨、拋光，用體積比為1…3…7的HF、HNO3、H2O組成的溶液腐蝕后，采用XJP-6A 型光學顯微鏡觀察顯微組織。

2 試驗結果與討論

2.1 流變應力曲線

由圖2可見：不同試驗條件下，變形初期在較小的應變ε下，TC21合金的應力σ都迅速攀升達到峰值，表現為明顯的加工硬化特性，此時位錯增加并發生積聚，位錯密度上升;隨著應變的繼續增加，不同條件的曲線呈現出不同的形態。在較小應變速率(0.001 s-1)下，當試驗溫度為870 ℃時，隨應變的增大，應力在達到峰值后以較快速率逐漸下降，在應變達到0.55左右時，應力下降到最低值，隨后應力開始緩慢上升，應力下降是由于發生了再結晶，曲線從最高點下降到最低點呈現了一個完整的動態再結晶過程，而再結晶后，晶粒細化，晶界變多，阻礙了位錯的滑移，導致位錯密度上升，曲線再次表現為加工硬化狀態；當試驗溫度升高到900 ℃時，流變應力曲線與870 ℃時明顯不同，存在兩個波峰，在第一個波峰后，應力逐漸下降，表現為動態再結晶軟化，在應變達到0.3左右時，應力達到最低值，而后應力逐漸上升，表現為加工硬化狀態，上升至第二個波峰后應力趨于平緩，表現為動態回復，隨后應力又開始逐漸上升；當試驗溫度為930，960 ℃時，曲線變化規律與870 ℃時一致，但變化幅度減小。當應變速率為0.01 s-1和0.1 s-1時，應力在迅速達到峰值后，基本都在不斷地減小，此時曲線呈現的是一個以動態再結晶為主的狀態，但動態再結晶不完全。當應變速率為1 s-1時，變形時間較短，沒有時間完成動態再結晶，曲線呈現的是以動態回復為主的狀態。另外，當試驗溫度(930，960 ℃)和應變速率(0.1，1 s-1)較高時，曲線存在明顯的鋸齒狀曲線段，文獻[9]對該現象進行了分析，認為合金在熱變形過程中發生了動態應變時效，其本質是溶質原子和位錯交互作用的結果，較高溫度下，溶質原子擴散移動速度足夠快，溶質原子向位錯附近聚集形成柯氏氣團，對位錯產生釘扎作用，表現為應力上升，較高應變速率下，位錯運動加快，脫離氣團后產生脫釘，表現為應力下降，這一過程不斷反復從而形成鋸齒狀流變應力曲線。

圖2 TC21合金在不同變形溫度及應變速率下的流變應力曲線

此外，由圖2還可知，在一定變形溫度下，流變應力隨著應變速率的提高而增大，如變形溫度為900 ℃時，應力峰值從應變速率為0.001 s-1時40 MPa左右增加到0.01 s-1時的70 MPa左右，再增加到0.1 s-1時的110 MPa左右，遞增幅度不斷增大，應力對應變速率敏感性逐漸增強。究其原因，在其他變形條件相同時，應變速率加快，加工硬化率變大，致使合金組織內部獲得更高的位錯密度，因此應力增大。同時，在一定應變速率下，流變應力隨溫度升高而降低，如應變速率為0.001 s-1時，應力峰值從溫度870 ℃時的55 MPa左右降低到900 ℃時的40 MPa左右，再到930 ℃時的32 MPa左右，遞減幅度不斷減小，應力對溫度敏感性逐漸減弱。這是由于變形溫度升高，原子活動加劇，擴散能力增強，促進了位錯滑移、攀移，宏觀上表現為應力不斷減小。

2.2 顯微組織

由圖3可知：在相同應變速率下，隨著變形溫度的升高，TC21合金組織中α相含量不斷減少，α相的尺寸先增大后減小，當變形溫度為930 ℃，應變速率為0.001 s-1時，組織中α相含量最少；這是由于隨著變形溫度的升高，變形溫度逐漸接近α→β相變點溫度(958.1 ℃)，而應變速率越低，α相有更長的時間轉變為β相。當變形溫度為870 ℃和900 ℃時，隨著應變速率的增大，β相含量逐漸減少，α相晶粒尺寸先減小后增大；在應變速率為0.001 s-1時，合金發生了充分的動態再結晶，且此時晶粒有足夠的時間長大，因此晶粒尺寸較大；在應變速率為0.01 s-1時，變形時間縮短，動態再結晶晶粒來不及長大，晶粒尺寸較小；在應變速率為0.1 s-1時，動態再結晶未發生完全，部分α相晶粒被拉長并破碎，少量細小的動態再結晶晶粒圍繞在條狀大尺寸α相晶粒周圍，這是變形和再結晶雙重作用導致的結果[10]；而當應變速率提高到1 s-1時，變形時間很短，變形以動態回復為主，晶粒尺寸較大。當變形溫度為930 ℃時，隨著應變速率的增大，β相晶粒發生了不完全的動態再結晶，晶粒細化，并且再結晶晶粒和α相晶粒夾雜在一起。

圖3 在不同變形條件下壓縮變形后TC21合金的顯微組織

2.3 本構關系的建立

2.3.1 流變應力本構方程

材料在熱變形過程中出現加工硬化、動態回復、動態再結晶等現象，使得合金的顯微組織發生變化。適當的熱變形條件可使變形后的顯微組織通過再結晶得到細化，提高合金的性能，而熱變形過程中動態再結晶的發生是由熱激活能控制的，材料在熱變形過程中各參數之間的關系可以通過本構方程來定量表達。Arrhenius方程被廣泛用于描述變形時應變速率、流變應力和溫度之間的關系，該方程在高溫下可以由Zener-Hollomon參數Z在指數型方程[11-12]中表示：

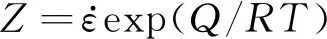
(1)

(2)

α=β/n1

(3)

SELLARS等[13]認為通過修正的Arrhenius雙曲正弦函數，可以更好地表達穩態流變應力、應變速率和溫度之間關系,修正后的函數方程為

(4)

式中：C和n2為常數。

在低應力階段，結合式(1)和式(2)可得:

(5)

對式(5)兩邊取對數得：

(6)

在高應力階段，結合式(1)和式(2)可得：

(7)

對式(7)兩邊取對數得：

(8)

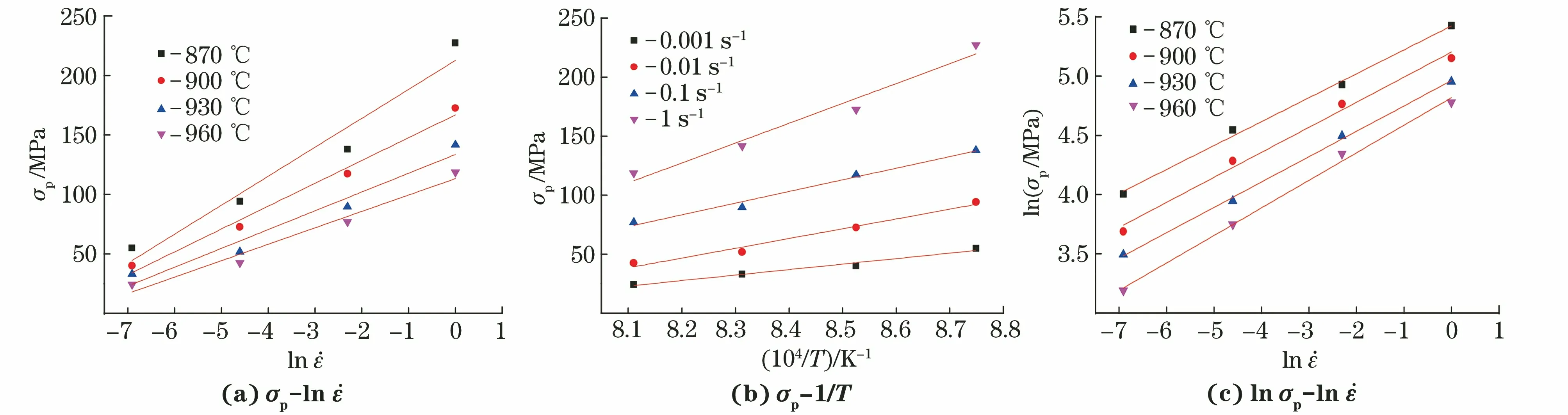
圖4 TC21合金壓縮變形時的峰值應力與熱變形參數之間的關系曲線

對式(4)兩邊取對數得：

(9)

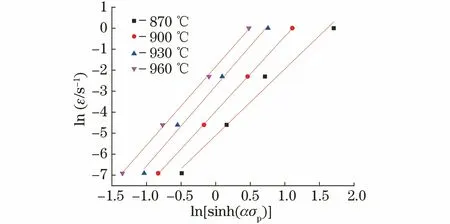
圖5 TC21合金壓縮變形時與ln[sinh(ασp)]的關系曲線

最終將上述所求得的Q,n2,C,α代入式(4)，可得TC21合金的熱變形流變應力本構方程：

exp[-450.835×103/(RT)]

(10)

用流變應力本構方程結合計算機模擬軟件可定量表征材料熱變形過程應力變化情況，因此方程計算的數據需要較準確。根據式(4)可進行變換得到下式用以計算峰值應力，并和試驗值進行對比，峰值應力計算公式為

(11)

將相關參數代入式(10)，用得到的峰值應力計算值和試驗值對比，如圖6所示。平均相對誤差計算公式[14]為

圖6 TC21合金壓縮變形中峰值應力計算值與試驗值的比較

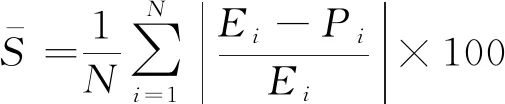
(12)

式中：N為峰值應力個數；Ei和Pi分別為峰值應力試驗值和峰值應力計算值。

通過計算得到平均相對誤差為6.274%，誤差范圍在10%以內，表明方程預測數據較準確。

2.3.2 動態再結晶位錯密度模型

由前面的試驗結果可知，變形溫度在870～900 ℃時，變形后合金顯微組織中α相的動態再結晶特征較為明顯，溫度為930 ℃時，由于相轉變使α相含量急劇減少，幾乎觀察不到α相的動態再結晶特征。為了更好地研究位錯對動態再結晶的影響，作者針對870 ℃下合金熱變形過程發生的動態再結晶，從位錯增殖的角度，基于位錯密度模型，定量表征動態再結晶的發生過程。其中，位錯密度ρ隨應變變化情況可用下式[15]來表達：

dρ=(h-rρ)dε

(13)

式中：h和r分別為加工硬化系數和動態回復系數。

r與應力和應變的關系[15]為

(14)

式中：σsat為動態回復應力；σ0為屈服應力。

由式(13)和式(14)，經過關系推導[16]可得：

(15)

式中：θ為應變硬化率，θ=dσ/dε。

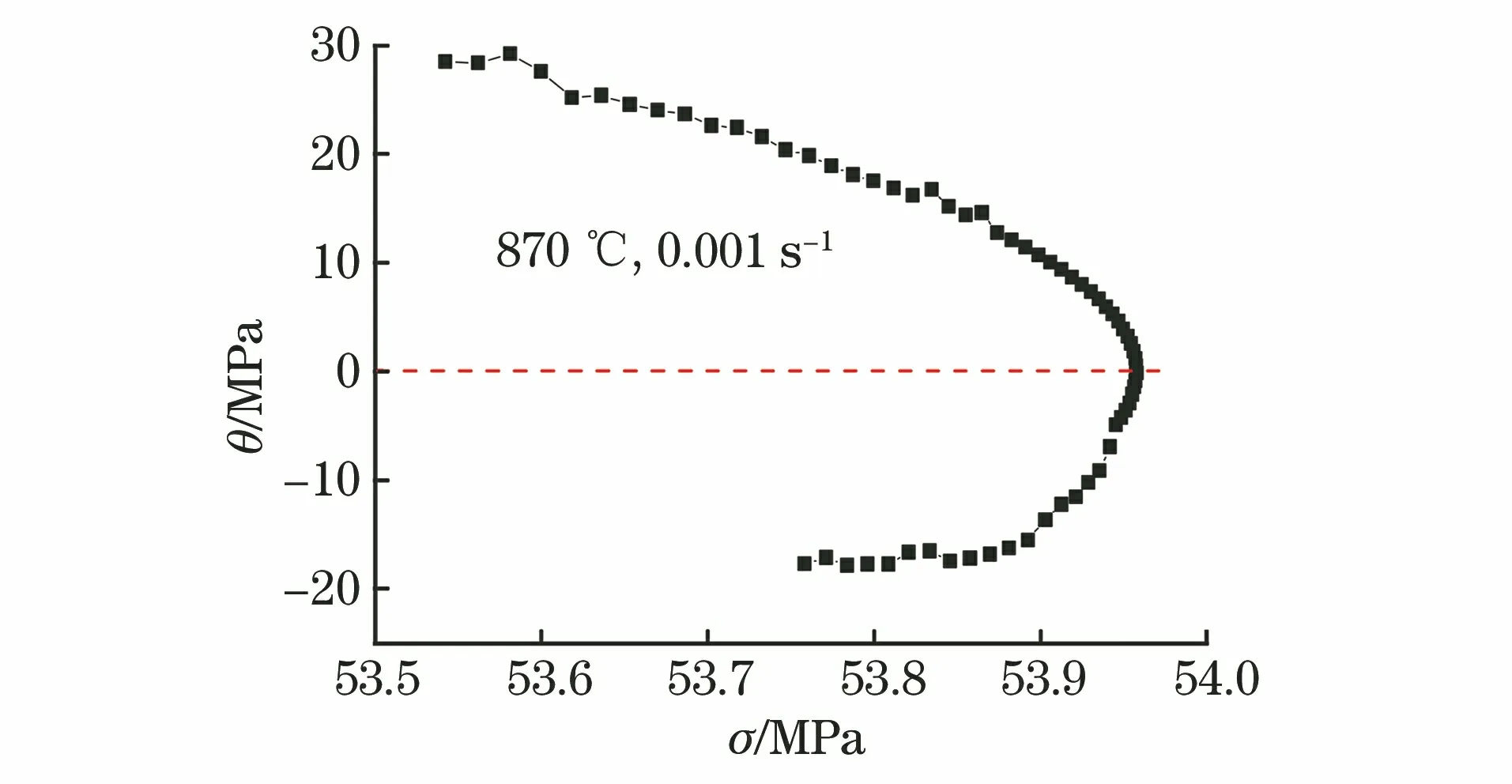
圖7 θ和σ的關系曲線

圖8 σ·θ和σ2的關系曲線

h與r之間的關系[15]為

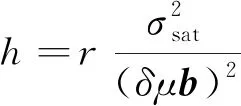
(16)

式中：δ為與位錯類型有關的系數，取0.5；μ為剪切模量，取26.09 GPa；b為柏氏矢量，取0.295 nm。

在上式中代入σsat,r,δ,μ,b，可計算出不同變形條件下的h。

在位錯密度模型中，加工硬化系數h和動態回復系數r[17]可表示為

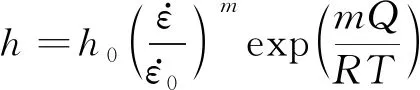
(17)

(18)

表1 計算得到870 ℃,0.001 s-1變形條件下TC21合金的各參數

2.4 顯微組織模擬

將TC21合金的的流變應力本構方程和動態再結晶位錯密度模型植入到DEFORM-3D軟件中，基于元胞自動機模塊，進行可視化的動態再結晶組織模擬。

由圖9可知，模擬得到在870 ℃時不同應變速率下，變形后的晶粒大小形態不一，當應變速率為0.001 s-1時，對比流變應力曲線可知在一次動態再結晶結束后，又發生了二次動態再結晶，最終晶粒形態呈均勻等軸狀，且晶粒有充足的時間長大，所以晶粒尺寸最大；應變速率提高至0.01 s-1時，動態再結晶后晶粒未長大，晶粒尺寸更為細小，對比觀察流變應力曲線，可知動態再結晶只發生了一次，并且發生較完全，說明此時應變速率提高，導致變形時間縮短，動態再結晶晶粒不會再持續長大而更為細小；應變速率繼續提高為0.1 s-1時，由于應變速率較快，動態再結晶未完全發生，觀察到條狀的大晶粒周圍圍繞著細小的動態再結晶晶粒，即α相晶粒被拉長并破碎，這是變形和動態再結晶雙重作用導致的結果。將模擬得到的顯微組織和試驗得到的顯微組織(圖3)進行對比，可知模擬顯微組織能較好地反映變形后的真實顯微組織。

圖9 模擬得到的TC21合金在870 ℃時不同應變速率下變形后的顯微組織

3 結 論

(1) TC21合金在應變速率為0.001～1 s-1、變形溫度為870～930 ℃的變形條件下，流變應力曲線形態主要呈現動態再結晶型，軟化機制以動態再結晶為主；變形溫度一定時，隨應變速率提高，應力對應變速率敏感性逐漸增強；應變速率一定時，隨變形溫度升高，應力對溫度敏感性逐漸減弱。

(2) 應變速率一定時，變形后TC21合金組織中α相含量隨變形溫度升高不斷減少，α相的尺寸先增大后減小，在變形溫度為930 ℃，應變速率為0.001 s-1時，α相幾乎完全轉變為β相；變形溫度為870 ℃和900 ℃，隨著應變速率增大，晶粒尺寸先因α相發生動態再結晶而變小，后因動態再結晶不完全或來不及發生，α相因變形作用被拉長而變大；當變形溫度升到930 ℃靠近相變點時，α相含量急劇減少，隨著應變速率增大，β相晶粒發生動態再結晶，晶粒細化。

(3) 對試驗數據進行線性擬合，獲得TC21合金在應變速率為0.001～1 s-1、變形溫度為870～930 ℃變形條件下的熱變形激活能為450.835 kJ·mol-1，建立了流變應力本構方程，驗證得到其平均相對誤差為6.274%；同時建立了870 ℃，0.001 s-1變形條件下的動態再結晶位錯密度模型，基于流變應力本構方程和位錯密度模型基礎上進行了動態再結晶組織模擬，模擬得到的顯微組織與試驗得到的顯微組織基本相符，說明計算模型較為準確。