預制空心保溫剪力墻試驗研究及延性分析

陳哲賢，劉文燕，楊 森，何文福，劉 威

（1.上海大學力學與工程科學學院，上海 200444；2.上海寶冶集團有限公司，上海 200941）

引言

裝配式剪力墻具有產業化生產、施工質量易保證、工期短和節能環保等諸多優點，得到了較為廣泛的應用［1－2］。裝配式剪力墻結構通常有三種形式，分別為預制實心剪力墻結構、預制疊合剪力墻結構和預制夾心保溫剪力墻結構［3］。

國外已開展了大量裝配式混凝土剪力墻試驗研究。SOUDKI等［4］和PEREA 等［5］針對豎向鋼筋采用預應力連接的裝配式混凝土剪力墻，進行了低周往復荷載試驗，研究表明：采用預應力鋼筋豎向連接的裝配式混凝土剪力墻耗能充分，具有良好的抗震性能。國內的研究對象主要針對預制實心混凝土剪力墻和預制疊合式混凝土剪力墻，重點研究了套筒灌漿連接以及漿錨搭接等不同豎向鋼筋連接方式對剪力墻抗震性能的影響。葉獻國等［6］和吳志新等［7］針對預制疊合式混凝土剪力墻進行了試驗研究，結果表明：預制疊合式混凝土剪力墻與現澆剪力墻的破壞形態和耗能能力相近；姜洪斌等［8］對采用預留孔道漿錨連接的三層足尺裝配式混凝土剪力墻結構進行了擬靜力試驗研究，認為預留孔道灌漿連接的預制構件變形能力較強，具有較好的抗震耗能能力。

預制夾心混凝土剪力墻由保溫板、內、外葉混凝土墻板以及連接件組成，該結構實現了隔熱保溫層與結構同壽命［9］。PALERMO 等［10］對某三層足尺預制夾心剪力墻結構進行了振動臺試驗研究，結果表明：根據歐洲規范進行設計的夾心剪力墻具有較好的抗震性能；薛偉辰等［11］開展了預制混凝土夾心保溫剪力墻的低周反復試驗研究，結果表明：預制夾心剪力墻的破壞模式為受彎破壞，與現澆剪力墻具有相近的耗能能力和延性；錢稼茹等［12］完成了套筒灌漿連接的三層裝配式夾心剪力墻足尺模型的擬動力試驗，研究結果表明：預制夾心剪力墻的內外頁墻體破壞形態不同，外葉墻不參與結構受力；朱元吉等［13］開展了不同連接形式PC 掛板－剪力墻擬靜力試驗研究，發現外頁墻板與剪力墻的粘結能力對剪力墻的承載能力有較大影響。上述研究中外葉墻不能參與結構受力，僅作為保溫材料的保護層；內外葉墻體通過連接件連接，其長期安全性能和耐久性能是否可靠還需工程的進一步檢驗。龔祖平等［14］提出了一種帶豎向接縫的模塊化自保溫混凝土剪力墻，并開展了擬靜力試驗研究，結果表明：自保溫預制剪力墻的屈服與峰值荷載與預制實心剪力墻相近，但延性低于實心剪力墻，且未提出改善延性的方案。

本文提出了一種新型預制空心保溫剪力墻（PHISW），為研究其抗震性能，對一個預制空心保溫剪力墻試件和一個現澆實心剪力墻試件進行低周往復加載試驗，分析PHISW 的承載力和延性?；谠囼灲Y果，采用ABAQUS 有限元軟件對墻體試件進行有限元分析，研究影響PHISW 延性的主要參數，進而提出預制空心保溫剪力墻的設計建議。

1 預制空心保溫剪力墻試驗研究

1.1 預制空心保溫剪力墻構造

PHISW 由內置的保溫芯材以及外圍混凝土構成，其構造如圖1（a）所示。采用內填保溫芯材聚氨酯提升剪力墻的節能保溫性能，通過適當提高混凝土強度提升剪力墻的承載力。這種結構體系不存在預制夾心保溫剪力墻結構體系中內外頁混凝土墻體的連接問題，墻體在工廠一體預制完成，養護后填入保溫芯材聚氨酯；同時也不需要現場大量澆筑混凝土，可直接在廠家預制完成后運到現場拼裝，通過灌漿套筒可實現上下剪力墻之間方便可靠的連接，圖1（b）為PHISW豎向鋼筋灌漿套筒連接示意圖。

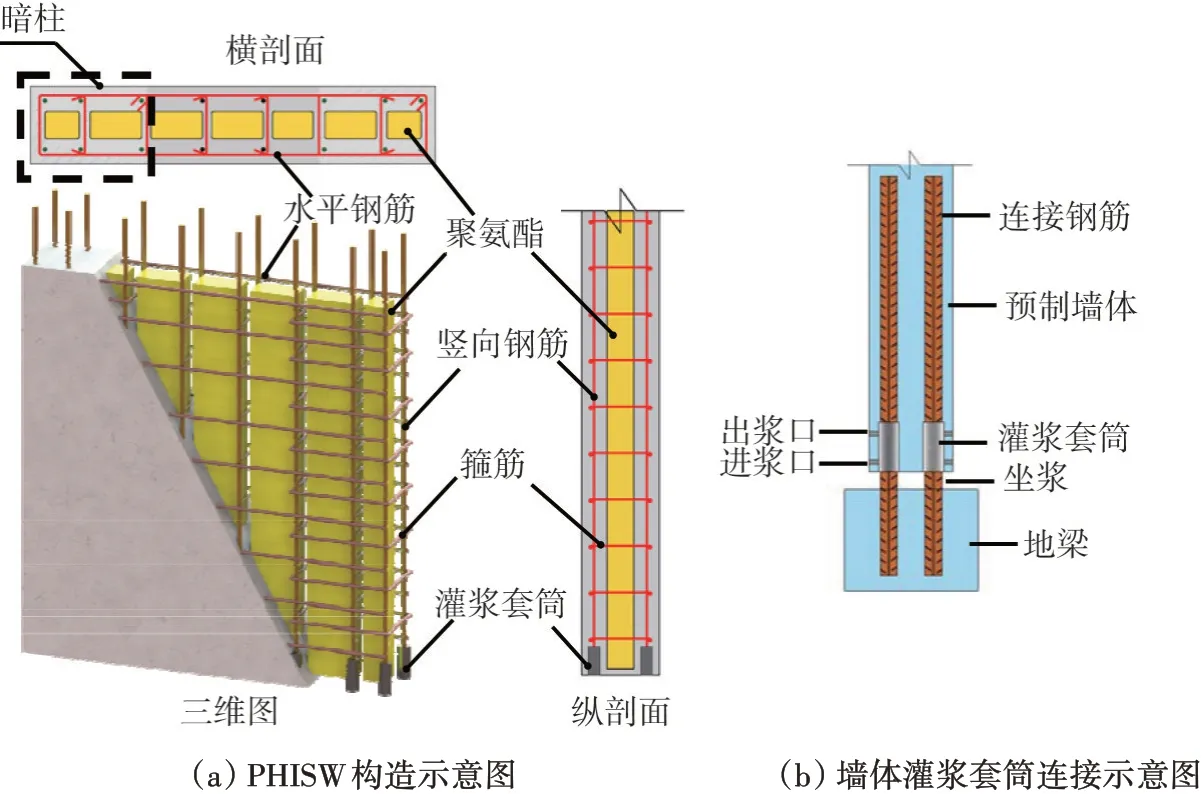
圖1 預制空心保溫剪力墻示意圖Fig.1 Precast hollow insulation shear wall

1.2 試驗簡介

本文進行了2片軸壓比為0.5的足尺剪力墻試件低周反復荷載試驗：1片為現澆剪力墻對比試件；另1片為預制空心保溫剪力墻試件，編號分別為CSW 和PMW，墻高均為2 900 mm，截面寬度1 300 mm。CSW 的墻厚為200 mm，考慮到等強度設計，PMW 的截面厚度設計為250 mm，試驗構件詳圖如圖2所示，設計參數以及部分試驗結果見表1。PMW 中陰影部分為內填的保溫材料聚氨酯，剪力墻中部兩列縱筋未貫通是因為在水平往復推覆下，剪力墻受壓受拉區域主要集中在墻體兩側暗柱，墻體中部區域受力較小，所以試驗時未將中部兩列縱筋插入地梁。墻頂設置加載用的鋼筋混凝土梁，墻底設置地梁，加載裝置如圖3所示。加載時首先由量程為5 000 kN的千斤頂提供豎向壓力，并在試驗過程中保持不變，設計軸壓比nd=1.2N/（fcA）：N為施加的豎向力，本文為2 240 kN；fc為混凝土軸心抗壓強度設計值；A為剪力墻截面面積。反力架下設置滑動支座，能使千斤頂與試件頂部位移保持同步。然后用1 000 kN 的水平作動器施加水平往復力，定義推力為正向加載，拉力為負向加載。加載時采用荷載與位移聯合控制的加載模式，試件屈服前采用力控制并分級加載，分別為20 kN和40 kN，每級循環一次；試件屈服后采用位移控制加載，分別為4 mm、8 mm和12 mm直至44 mm，每級循環3次，試驗加載制度如圖4所示。

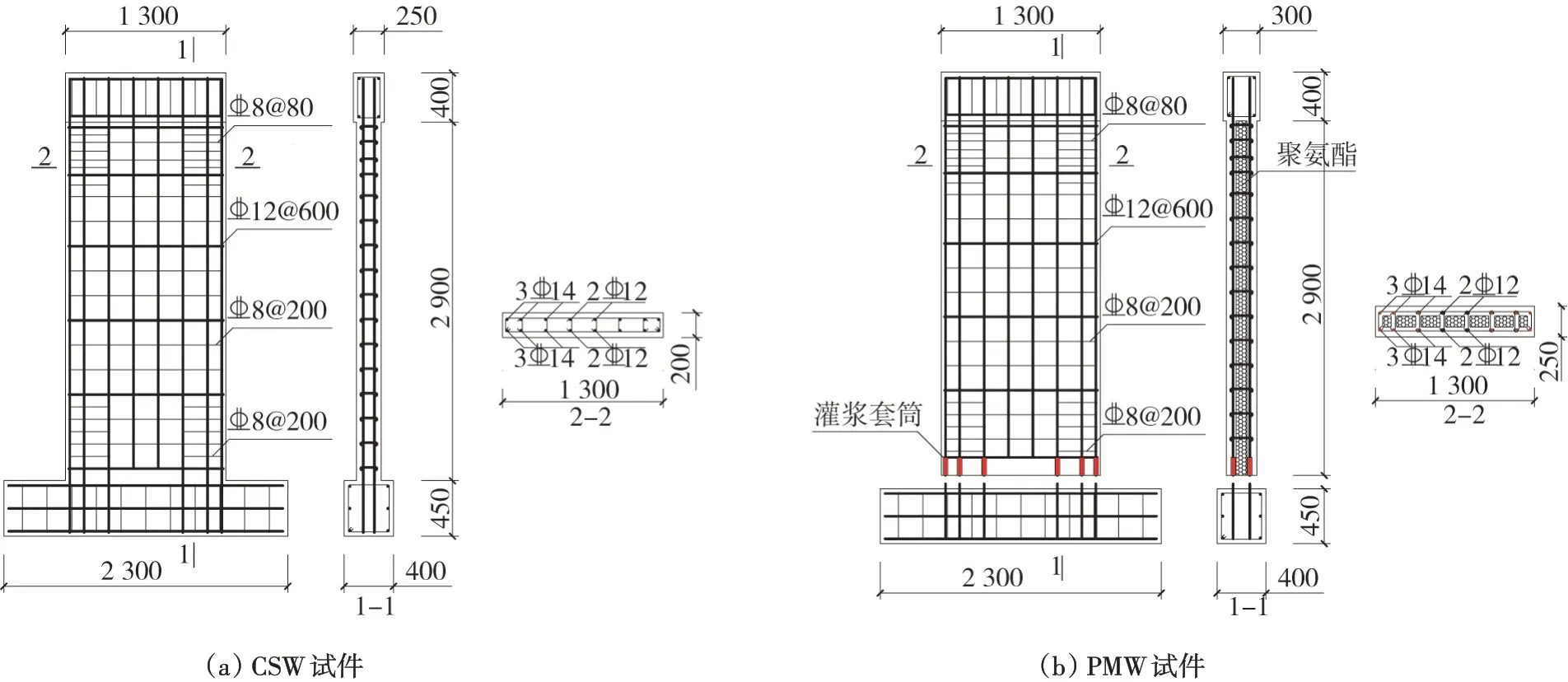
圖2 試驗構件詳圖Fig.2 Details and dimensions of the specimens

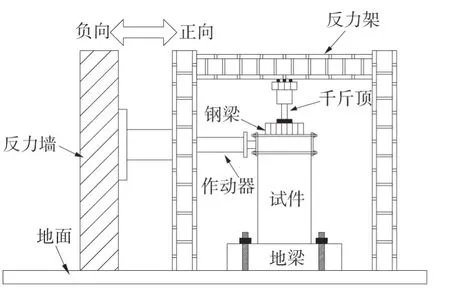
圖3 加載裝置Fig.3 Testsetup

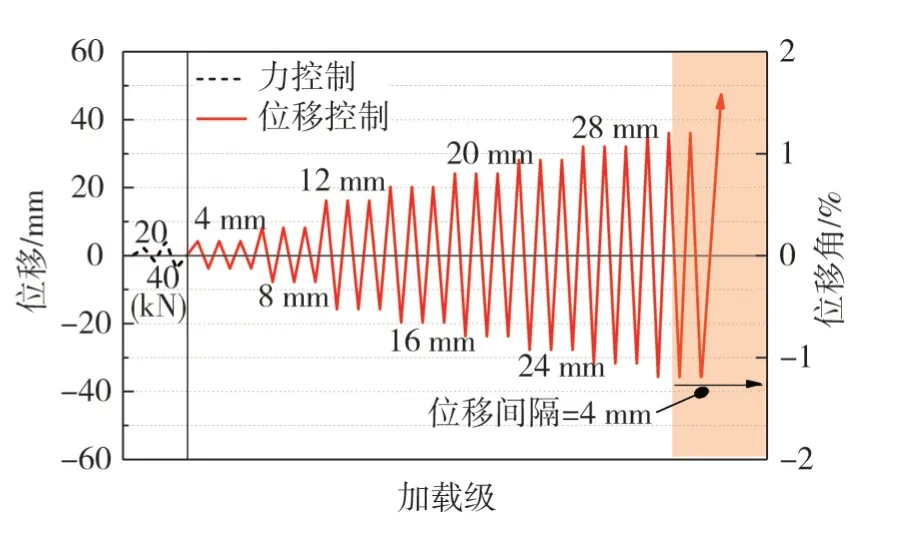
圖4 試驗加載制度Fig.4 Loading scheme

表1 各試件主要參數及主要試驗結果Table 1 Specimen description and main test results

試驗的現場裂縫照片以及滯回曲線分別見圖5－6，試驗表明：（1）試件墻體底部兩邊先出現水平裂縫，隨著荷載增加，水平裂縫逐漸發展為試件中部的對角斜裂縫；（2）2個試件的裂縫開展模式類似，以彎曲破壞為主，CSW試件的裂縫開展更充分，底部混凝土壓潰區域更小，滯回曲線更飽滿，耗能能力更強；（3）從表1以及圖6可以看出：2個試件峰值承載力相近，但PMW 試件的延性系數僅為CSW 的63%，且未超過3，表明預制空心保溫剪力墻試件的延性較弱，因為PMW 試件是空心的，從截面上看：混凝土受壓面小，受壓時更容易被壓潰，從而喪失承載力。

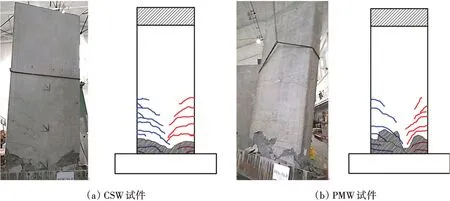
圖5 試件破壞模式Fig.5 Crack patterns under cyclic loading

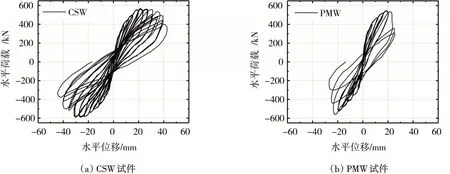
圖6 試驗滯回曲線Fig.6 Hysteresis loops

2 有限元建模和驗證

2.1 有限元模型建立

利用ABAQUS 對結構擬靜力試驗過程進行模擬。鋼筋和混凝土分別采用三維桁架單元（T3D2）以及八節點線性六面體三維實體單元（C3D8R）模擬。為滿足計算精度和穩定性，墻體混凝土和鋼筋的網格按單元長度50 mm左右進行劃分，加載梁和地梁單元則按100 mm劃分。鋼筋和混凝土的相互作用通過前處理中的Embed 命令定義，忽略鋼筋與混凝土之間的黏結滑移［15］。由于保溫材料聚氨酯對結構承載力貢獻極小，所以PMW 建模忽略聚氨酯的作用，直接按空心混凝土墻體進行建模。因為實際施工時PMW 墻體混凝土與地梁之間需要坐漿，所以模擬時墻體底面和地梁表面需定義接觸關系，接觸面采用庫倫－摩擦模型，法向定義為硬接觸，切向采用罰函數進行計算，摩擦系數取0.6［16］。CSW 試件建模時墻體與地梁接觸關系直接按綁定設置。相關文獻［17］研究表明：預制剪力墻豎向鋼筋采用灌漿套筒連接能等同現澆，同時也為模型計算更容易收斂，建模時未考慮灌漿套筒。

為較好的模擬混凝土在低周往復荷載下的性能，墻體混凝土采用塑性損傷模型（CDP）［19］，如圖7 所示，混凝土膨脹角取30°，粘滯系數取0.004，其余損傷塑性參數取ABAQUS 的默認值，損傷因子采用基于能量等價原理的計算方法［18］。應力－應變關系采用我國《混凝土結構設計規范》（GB 50010－2010）中的推薦曲線。由于加載梁和地梁混凝土不是重點分析對象，其本構采用彈性關系。本文中鋼筋的本構關系采用的是雙線性硬化本構模型，鋼筋硬化段斜率取初始彈性模量的千分之一，屈服強度與實測值保持一致，如圖8所示。

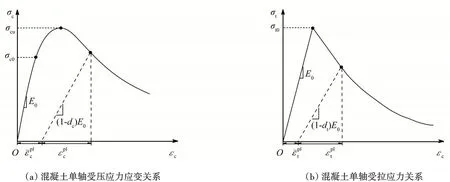
圖7 CDP模型單軸受拉和受壓本構關系Fig.7 Tension and compression curves of concrete under uniaxial loading

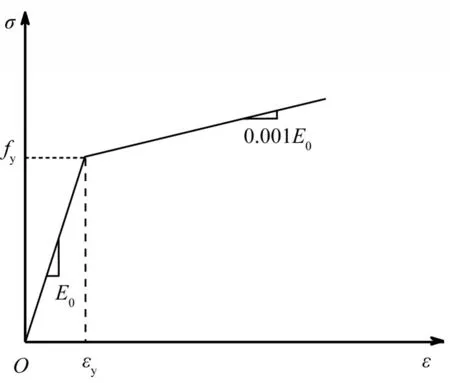
圖8 鋼筋雙線性硬化本構關系Fig.8 Bilinear hardening model of reinforcement

試件有限元分析模型見圖9，約束地梁底面的平動自由度以模擬試驗的邊界條件，同時約束加載梁頂面U2自由度防止加載時模型出現平面外變形，導致模型收斂困難。分析過程分為兩步：第1步為荷載控制，在加載梁頂面施加等效豎向面荷載，使墻體軸壓比與試驗一致；第2 步為位移控制加載，在加載梁左側的耦合點上施加控制位移，位移加載制度與試驗保持一致。

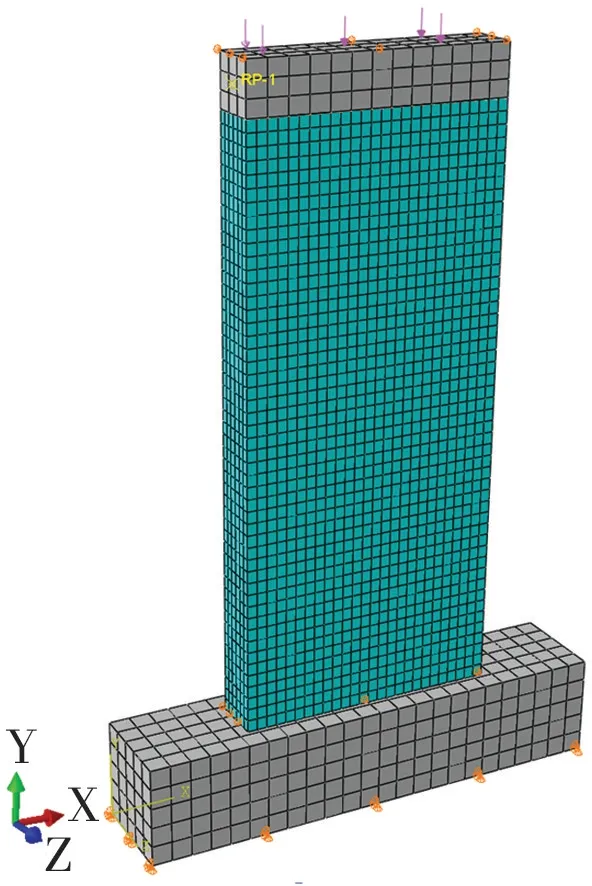
圖9 有限元分析模型Fig.9 Finite element model

2.2 有限元模型驗證

圖10為試件有限元模擬的荷載位移滯回曲線與試驗對比圖。從圖中可以看出：有限元分析得出的滯回曲線與試驗結果基本一致，峰值承載力比較接近，誤差在10%以內，見表2。但是有限元分析得到的試件的整體剛度大于試驗結果，分析其原因為：在數值模擬中，鋼筋直接嵌入混凝土，未考慮鋼筋和混凝土之間的粘結滑移；而試驗過程中，隨著荷載的增加，混凝土和鋼筋以及鋼筋和套筒灌漿料之間的粘結存在退化［20］。圖11 給出了數值模擬2 個試件的混凝土損傷破壞情況，圖中DAMAGEC 以及DAMAGET 云圖分別對應混凝土的受壓和受拉損傷，即試驗中混凝土的受壓剝落以及受拉開裂。由圖11可知：2個試件墻體的損傷不同，CSW 試件受拉損傷范圍更廣，而PMW 墻體底部混凝土受壓損傷區域更大，這也與試驗觀察到的現象一致（圖5），所以能夠使用有限元方法對預制空心保溫剪力墻進行分析計算。

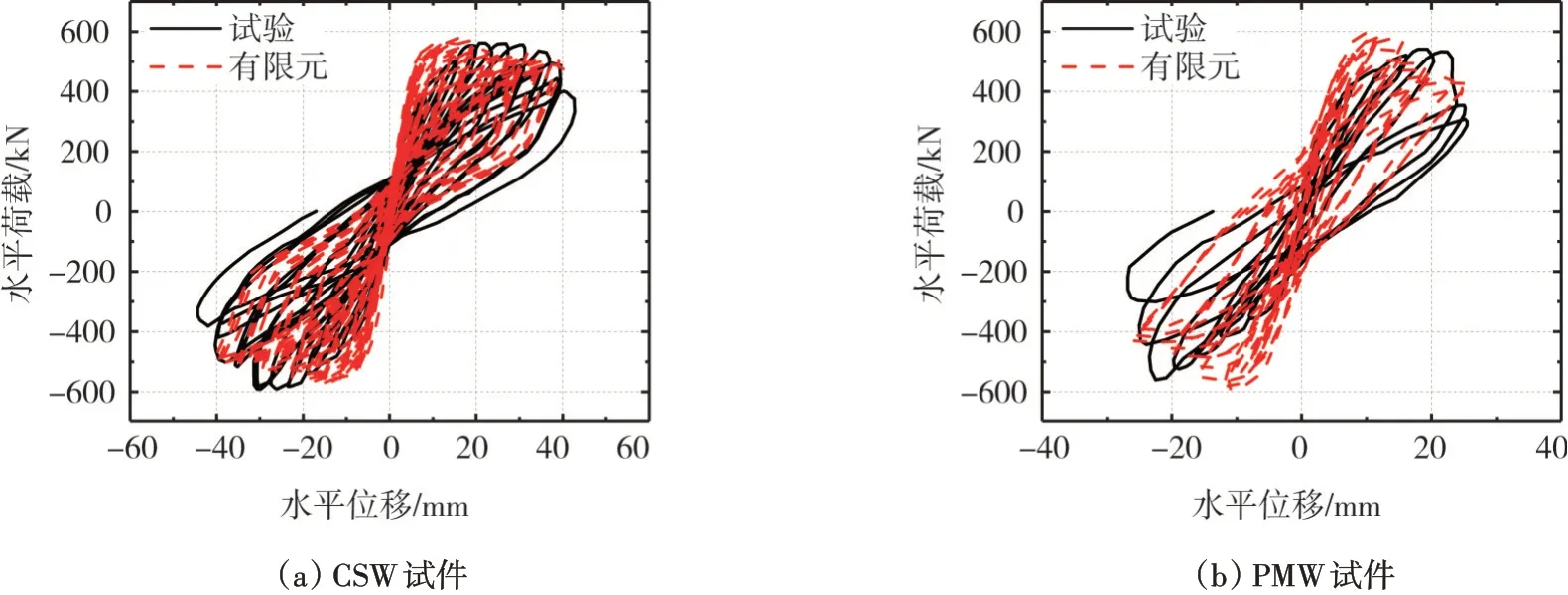
圖10 有限元與試驗的滯回曲線對比Fig.10 Comparison of hysteresis curves between finite element model and test

表2 試驗和數值模擬峰值承載力對比Table 2 Comparison between experimental and numerical strengths of the specimens

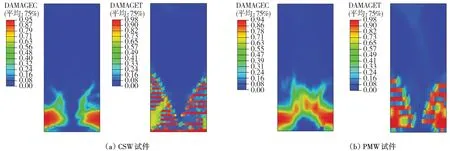
圖11 混凝土損傷數值模擬分析結果Fig.11 Concrete damage in numerical simulation

3 延性影響參數分析

試驗研究表明：按承載力設計并不能保證預制空心保溫剪力墻具有良好的延性。比較合理的方法，是以延性要求為基礎設計剪力墻［21］。因此，有必要研究如何提高預制空心保溫剪力墻的延性。結合試驗結果以及相關文獻［22－23］研究，本文采用單因素設計方法，細化墻體軸壓比n、暗柱箍筋直徑d和間距s、暗柱縱筋配筋率ρ以及空心率e這4個變化參數，各參數取值見表3，共設計了74個試件進行有限元分析。

表3 有限元分析參數取值Table 3 Parameter of finite element analysis

3.1 軸壓比

剪力墻是片狀結構，受力不同于柱，其軸壓比的限值應比柱更為嚴格［24］，為此著重研究軸壓比對PHISW延性的影響。圖12（a）和圖12（b）分別給出了在不同的暗柱箍筋直徑以及暗柱縱筋配筋率下，剪力墻的延性系數與軸壓比的關系。從圖中可以看出：隨著軸壓比的增加，PHISW 的延性系數呈現明顯的下降趨勢，說明軸壓比太大，墻體的延性會變差。

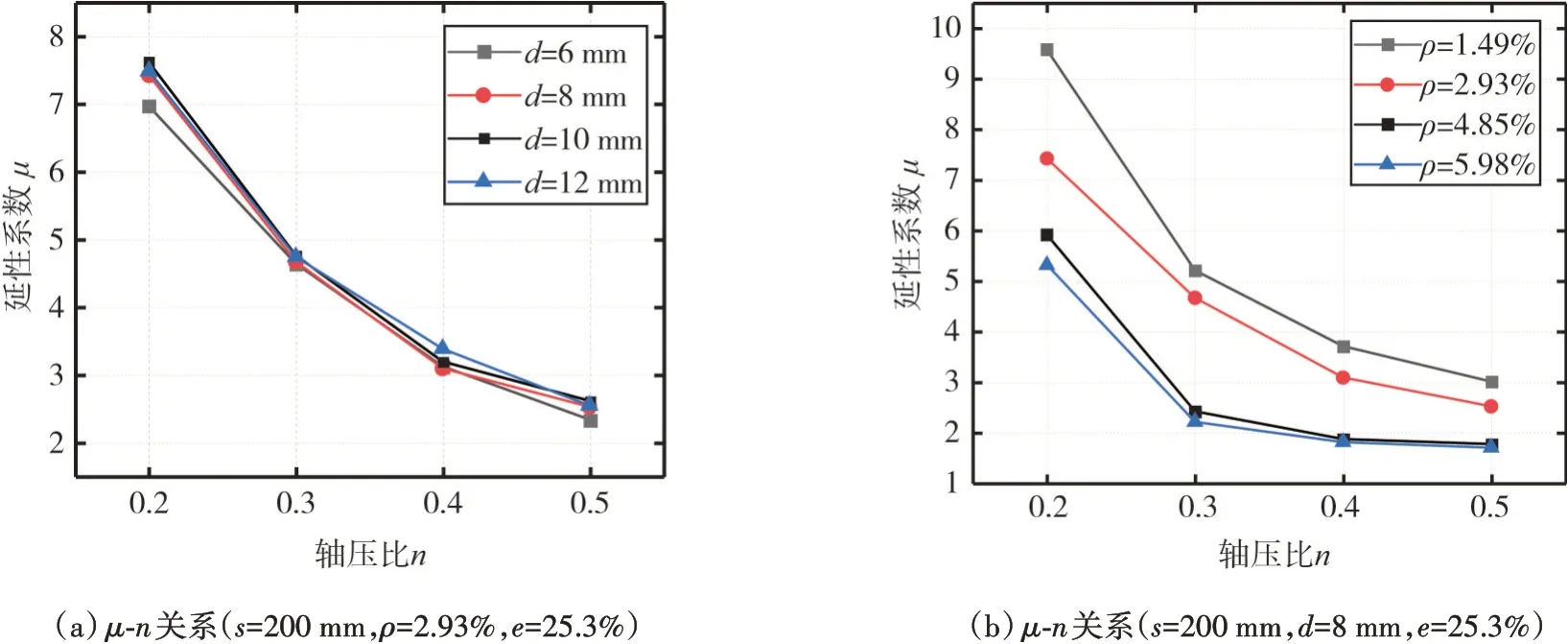
圖12 延性系數與軸壓比關系Fig.12 Relationship of ductility and axial compression ratio

此外，延性系數在軸壓比為0.4時為一轉折點，軸壓比從0.2增大到0.4過程中，延性系數降低較快，軸壓比超過0.4 之后，延性系數降低較慢。軸壓比為0.5 時的預制空心混凝土剪力墻延性已經較差，因此在設計中為了保證構件的延性應嚴格控制軸壓比，PHISW軸壓比不宜大于0.4。

3.2 暗柱箍筋直徑與間距

圖13（a）和圖13（b）分別給出了不同軸壓比下，PHISW 的延性系數分別與暗柱箍筋直徑d以及暗柱箍筋間距s的關系。由圖13（a）可以看出：隨著d的提高，延性系數基本呈一條水平直線，說明暗柱箍筋直徑對PHISW 的延性影響很小。由圖13（b）可知：在0.4 的軸壓比之前，PHISW 的延性隨著暗柱箍筋間距增大而減小，隨著軸壓比的增大，延性減小幅度逐漸降低，與不配置箍筋相比，200 mm的暗柱箍筋間距具備約束能力。

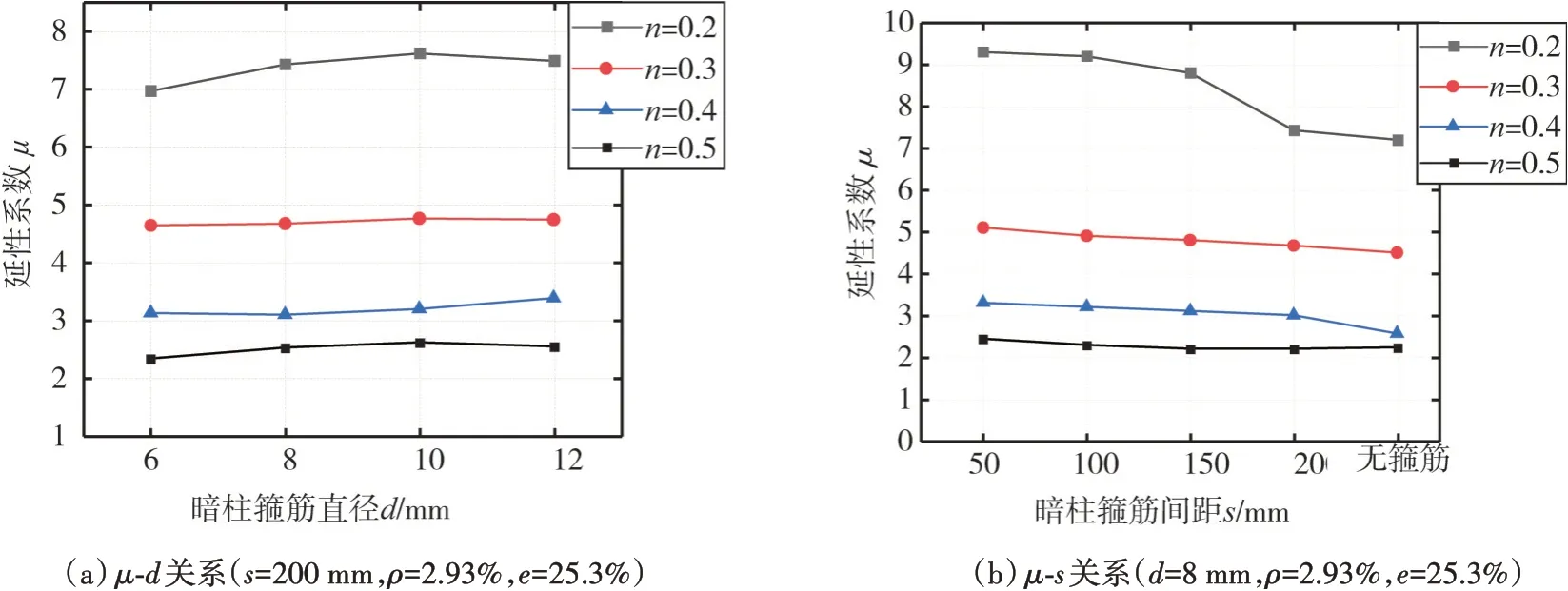
圖13 延性系數與暗柱配箍關系Fig.13 Relationship of ductility and stirrup reinforcement of concealed column

暗柱箍筋間距對PHISW 延性的影響程度大于箍筋直徑的影響，但在大于0.3的軸壓比后，暗柱箍筋直徑以及間距的影響均較小，設計時建議采用我國《高層建筑混凝土結構技術規程》（JGJ 3-2010）（簡稱“《高規》”）中表7.2.16中的建議取值，在按二級抗震設計時，建議暗柱箍筋最小直徑取8 mm，最大間距取150 mm。

3.3 暗柱縱筋配筋率

圖14（a）和圖14（b）分別給出了不同軸壓比以及不同暗柱箍筋直徑下，PHISW 的延性與暗柱縱筋配筋率ρ的關系。由圖14 可以看出：隨著ρ的提高，延性系數會下降，主要原因是高配筋率構件，變形能力會減弱［25］。由圖14（a）可知：當軸壓比超過0.3后，不同ρ下構件的延性會很接近，說明在高軸壓下，暗柱縱筋配筋率對構件延性的影響會降低。

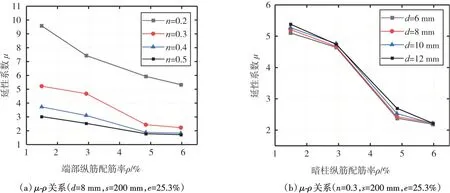
圖14 延性系數與暗柱縱筋配筋率關系Fig.14 Relationship of ductility and reinforcement ratio of concealed column

因為暗柱縱筋配筋率對承載力有較大影響，為綜合評判PHISW 的受力性能，圖15列出了軸壓比0.3時，PHISW 在ρ分別為1.49%、2.93%以及4.85%時的滯回曲線，編號分別為PW－1、PW－2和PW－3。數值模擬得出的峰值以及極限承載力列于表4，其中：Fu取Fp的85%；FM以及FV為分別按照《高規》中偏心受壓剪力墻正截面受壓承載力以及斜截面受剪承載力公式計算對應的水平力；Fc為FM和FV中的較小值。計算時對PHISW 的中間空心墻體部分采用截面簡化法［26］，即將PHISW 墻體等效為實心剪力墻。由圖15 以及表4 可知：PW－1 以及PW－2 為壓彎破壞，滯回曲線較PW－3 更為飽滿，延性較好，極限位移角θu大于1/120，滿足剪力墻彈塑性位移角限值要求；而PW－3 為壓剪破壞，雖然承載力較高，但加載后期承載力下降得更快，延性較差。建議暗柱縱筋配筋率ρ取值不小于1.49%，且不超過3%。

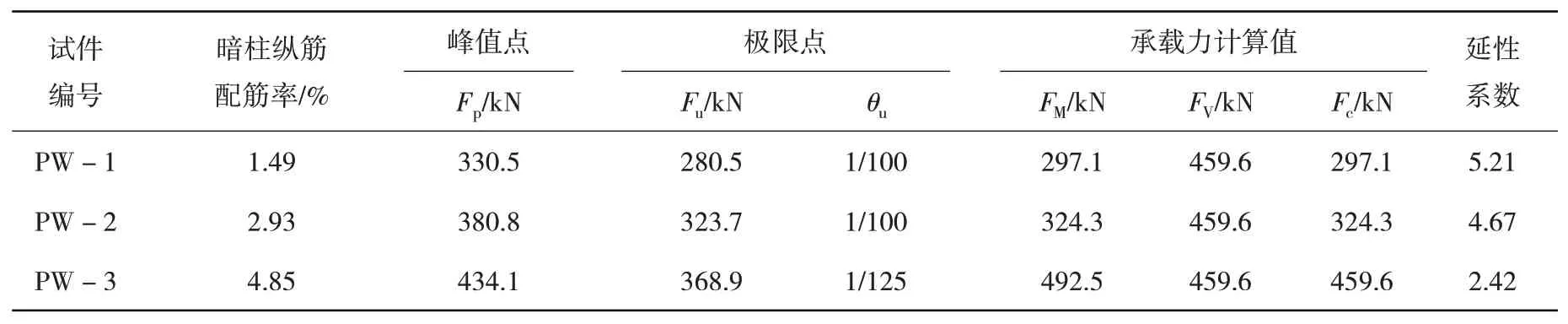
表4 不同ρ下數值模擬結果Table 4 Numerical simulation results underunder different longitudinal reinforcement ratio

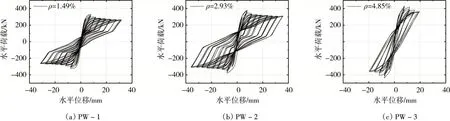
圖15 不同ρ下PHISW 的滯回曲線Fig.15 Hysteretic curve of PHISW under different reinforcement ratio

3.4 空心率

圖16給出了不同軸壓比下，PHISW 延性與空心率e的關系，e=（Ap/Aa）×100%，Ap為空心部分面積，Aa為剪力墻全截面面積。由圖可知：隨著空心率的增加，試件延性呈下降趨勢，原因是空心率越大，墻體底部混凝土受力面更小，更容易被壓潰。剪力墻延性多大為宜，規范尚無規定，本文以位移延性系數3.0為目標［21］，在軸壓比不超過0.4時，空心率不宜大于25%。

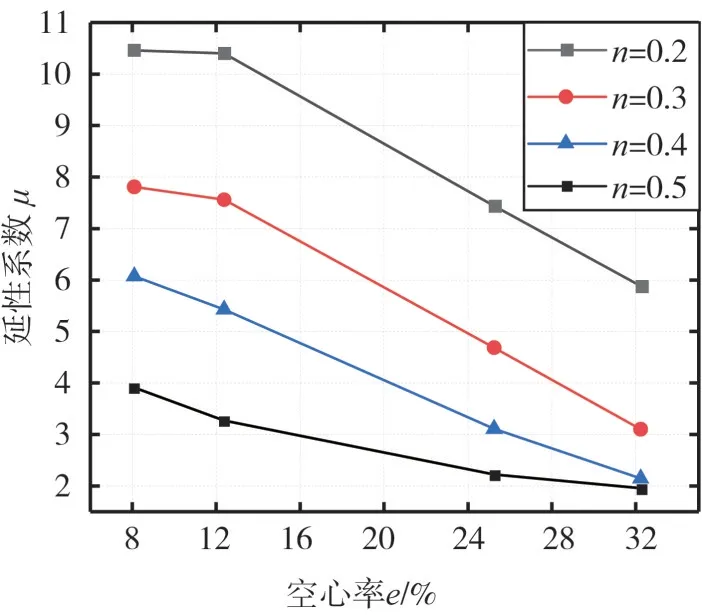
圖16 延性系數與空心率關系Fig.16 Relationship of ductility and hollow ratio

4 結論

（1）預制空心混凝土保溫剪力墻以彎曲破壞為主，承載能力與現澆剪力墻等同，但延性系數略低。ABAQUS數值模擬得出的滯回曲線、破壞模式與試驗結果基本吻合。

（2）軸壓比是影響預制空心保溫剪力墻延性的主要因素，隨著軸壓比的增加，位移延性系數呈下降趨勢。為保證構件有較好的延性，軸壓比設計值不宜大于0.4。

（3）暗柱配箍對預制空心混凝土保溫剪力墻的延性影響較小，設計時建議按照我國《高規》的建議取值，箍筋直徑不宜小于8 mm，箍筋間距不宜大于150 mm。

（4）暗柱縱筋配筋率對預制空心混凝土保溫剪力墻延性的影響較大，隨著暗柱縱筋配筋率增大，剪力墻延性降低，但在高軸壓下，暗柱縱筋配筋率對構件延性的影響會降低。為滿足低軸壓比下剪力墻彈塑性變形能力與“強剪弱彎”的設計要求，建議暗柱縱筋配筋率取值為1.49%～3%。

（5）空心率對預制空心保溫剪力墻延性影響較大，隨著空心率的增加，延性呈下降趨勢，建議空心率不宜大于25%。