逆變站動態特性對直流傳輸容量的影響分析

文彬彬

（長沙理工大學 電氣與信息工程學院，湖南 長沙 410000）

柔性直流輸電VSC－HVDC技術以其有功和無功單獨調節[1]、無源供電能力[2－3]和便于搭建直流電網[4]等優勢，吸引了很多學者的關注。直流輸電沒有高壓交流輸電的同步穩定問題，這是它的獨特優勢，但是基于VSC型的換流站具有很快的控制恢復效果，會在逆變站中產生負阻尼效果的恒功率特性，這一負荷特性將直接約束直流電壓的穩定性并限制系統直流傳輸容量的大小。

在分析系統直流傳輸容量和直流電壓穩定性之前，首先需要對VSC－HVDC系統受端側進行直流側小信號建模。文獻[5]建立了海島VSC－HVDC系統的整流站、直流電纜和逆變站的全局小信號阻抗模型。文獻[6]建立了不受短路容量限制的雙端VSC－HVDC系統小信號模型，模型的準確性通過了仿真驗證。文獻[7]建立了基于電流控制的雙端VSC－HVDC系統的小信號模型，并設計了抑制系統低頻振蕩、增加系統阻尼的控制器。文獻[8]使用雅克比傳遞矩陣的形式對基于電壓源型變流器和其交流系統進行了小信號建模。文獻[9]通過狀態空間法，建立了不受交流系統強度約束的雙端柔性直流輸電系統小信號模型，具有普遍適用性。文獻[10]針對線性負荷供電的DC／AC變流器，對其進行了直流側建模，便于分析變流器的負阻抗特性。文獻[11]為了研究諧振在直流系統中的影響，對柔性直流輸電系統中的變流器進行了阻抗建模。文獻[12]對狀態空間平均方程下的DC／AC變流器進行了等效建模，并分析了系統的動態和靜態性能。上述文獻建立了不同工程需要的直流側小信號模型，但在分析穩定性時不具備推廣性，其沒有進一步分析動態特性對直流電壓和直流傳輸容量的影響。

本文著重研究了VSC－HVDC系統中受端逆變站的直流側小信號模型的建立，并分析逆變站的動態特性（負荷恢復速度等）對直流電壓穩定性和直流傳輸容量的影響。

1 系統建模

1．1 VSC－HVDC系統描述

圖1為雙端VSC－HVDC系統結構圖。系統由整流站、逆變站和直流線路構成，其中直流側線路作為橋梁串接整流站和逆變站構成雙端系統，送端和受端的交流側均與大電網連接，Req、Leq和Ceq分別代表直流線路的等效線路參數，R、L分別表示交流線路的變壓器和電抗器的等效參數，us1、us2、u1、u2分別表示PCC點的電壓和換流器出口電壓，udc1、udc2表示直流側電壓，其中帶有下標1、2的分別表示整流站、逆變站的參數。

圖1 VSC－HVDC系統結構圖

1．2 換流站控制系統模型

針對圖1的VSC－HVDC系統，送端部分使用定無功控制和定直流電壓控制方式，受端部分則采用定有功功率和定無功功率的方式。以受端逆變側換流站為例，為實現有功和無功的解耦控制[13－14]，采用含有內環電流解耦控制器的系統結構（如圖2所示）。圖中，us2d、us2q分別為PCC2點電網電壓的d、q軸分量；u2d、u2q是交流側的d、q軸電壓分量；是內環電流控制期望輸出的d、q軸電壓分量；is2d、is2q是電網的d、q軸電流分量；是外環控制器產生的有功、無功電流值。

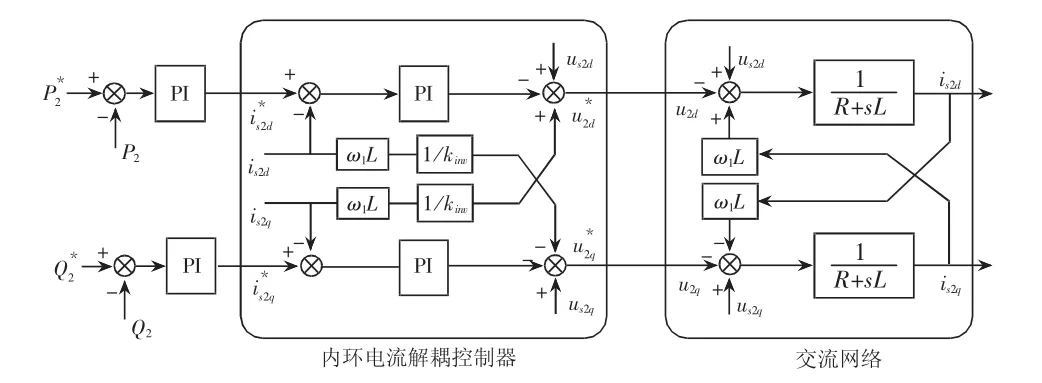
圖2 換流站控制系統結構圖

在逆變站采用電流解耦控制后，有功、無功電流控制可以分解成兩個獨立的控制環[15－16]。這樣就可以用一階慣性簡化代替。圖3為簡化后的換流站功率控制系統結構圖，圖中Gcur（s）＝1／（1＋sτ）是電流環的傳函。

圖3 換流站功率控制系統結構圖

式（1）是將上圖的功率控制環進行合并得到的閉環傳函，式（2）是標準二階系統的閉環傳函，其中ξ是系統的阻尼比，T是系統的響應時間。

對比式（1）、式（2）兩個傳遞函數，得到功率環的控制參數Kp和Ki與其響應時間常數T的關系式如下：

2 逆變站的直流側小信號模型

3 直流電壓穩定性分析

3．1 VSC－HVDC系統簡化電路

在分析逆變站的負荷特性對穩定性和傳輸容量的影響時，用理想直流電壓源替代整流站，得到如圖4所示的VSC－HVDC系統簡化電路，圖中Req和Leq是等效電阻和等效電感，Ceq為等效電容，Zdc是逆變站小信號輸入阻抗模型。

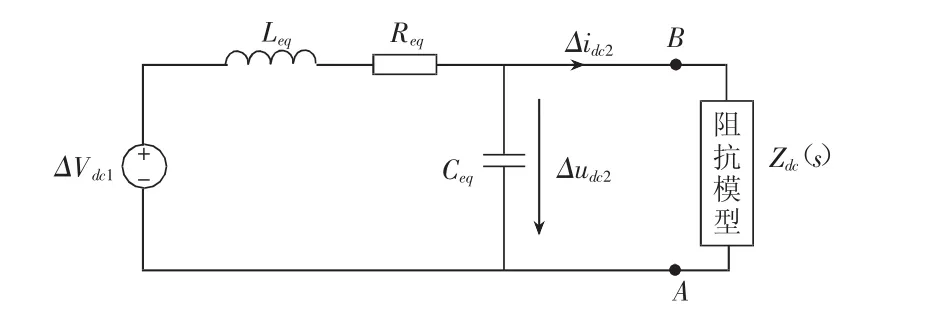
圖4 VSC－HVDC系統簡化電路

3．2 直流傳輸容量的計算

根據VSC－HVDC系統的簡化模型，令方程X（s）＝0，通過計算特征根是否在左半平面判斷系統的穩定性。基于此，本文關于VSC－HVDC系統直流傳輸容量的計算步驟如下：

（1）給功率Pdc賦初始值；

（2）在功率Pdc上增加一個小增量△Pdc；

（3）使Pdc＝Pdc＋△Pdc，每得到一個Pdc，相應計算出所有特征根的值；

（4）重復步驟（2）和（3），直到公式（22）－（26）中的任何一個特征根的實部大于零轉至步驟（5）；

（5）將步驟（3）中得到的功率減去△Pdc就是系統的直流傳輸容量Pdc＿max。

3．3 逆變站動態特性對直流傳輸容量的影響分析

根據上述建立的求取直流傳輸容量的步驟，得到了不同響應時間常數T下直流傳輸容量的曲線圖如圖5所示，其中逆變站響應時間常數T與控制參數Kp、Ki的對應關系如表1所示。

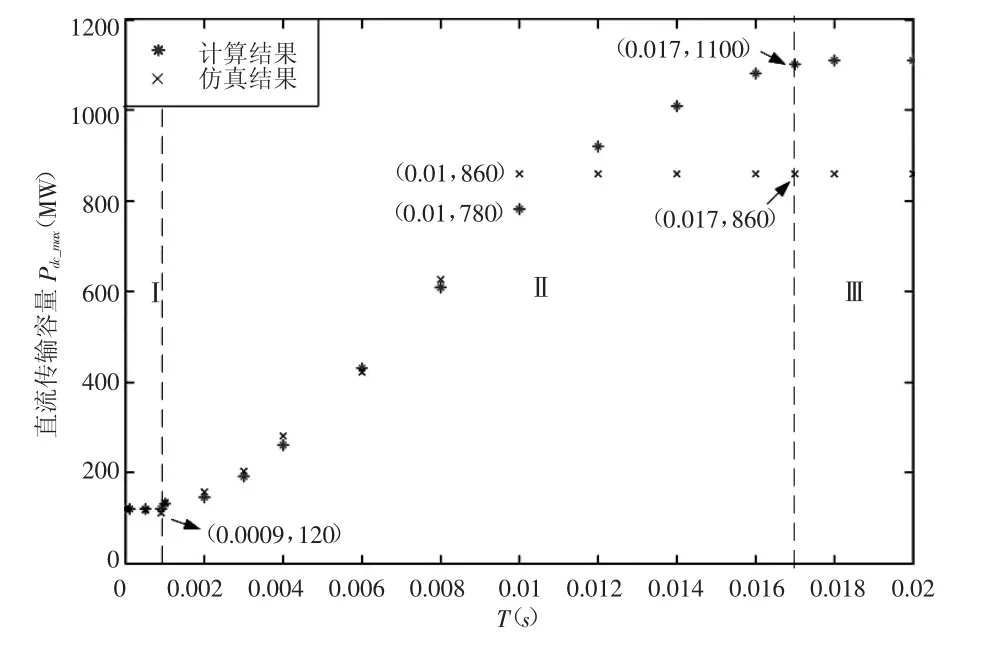
圖5 時間常數T與直流傳輸容量的關系圖

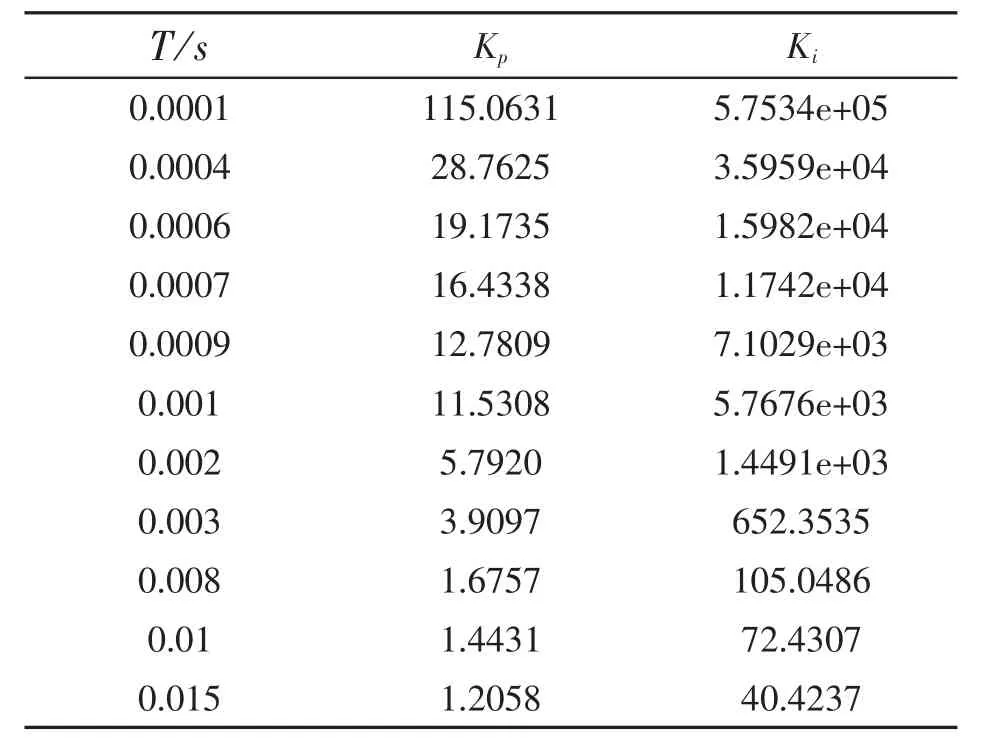
表1 控制參數對應表

4 仿真分析

在PSCAD／EMTDC中搭建如圖1所示的雙端VSC－HVDC系統模型來驗證本文建立的數學模型的正確性。表2為VSC－HVDC系統參數表。內環電流控制器中的Kp、Ki可根據式（1）、式（2）求得，部分參數的取值如表1所示。

表2 VSC－HVDC系統參數表

可以把圖5分為3個區域，并結合穩定條件分析可知：

（1）區域Ⅰ：T很小，響應速度很快，在毫微秒級以下，此時系統直流傳輸容量Pdc＿max受T變化的影響較小，若將逆變站等效于恒功率負荷[11]，即Rdc＝－udc20／idc20，所計算的系統直流傳輸容量與該區域的傳輸容量相等。

（2）區域Ⅱ：當T大于某值時，時間常數T與傳輸容量Pdc＿max呈正相關。

（3）區域Ⅲ：當T繼續增加，并達到某個界限后，直流傳輸容量Pdc＿max將不受T的影響。

4．1 區域Ⅰ范圍內的響應時間常數對系統直流傳輸容量的影響

根據上述步驟可以得到時間常數T為0．1ms和0．5ms時系統直流傳輸容量Pdc＿max都為120MW，分別如圖6和圖7所示，在5s時把系統功率從100MW增大到110MW和117MW，從圖中可知，當功率增大到110MW時系統仍然穩定，但是當功率增大到117MW時系統開始了功率振蕩。可以得出結論，當逆變站響應時間常數T很小時，響應時間常數T對系統直流傳輸容量Pdc＿max的影響很小，可用恒功率負荷等效代替VSC－HVDC系統的逆變站。

圖6 時間常數為0．1ms時的直流傳輸容量圖

圖7 時間常數為0．5ms時的直流傳輸容量圖

4．2 區域Ⅱ范圍內的響應時間常數對系統直流傳輸容量的影響

根據上述步驟可以得到時間常數T為2ms和4ms時系統直流傳輸容量Pdc＿max，它們是150MW和270MW。圖8是仿真在響應時間常數為2ms時的直流傳輸容量圖。在5s時把功率從100MW增大到150MW和160MW，由圖可知，當功率增大到150 MW系統仍然穩定，但是當功率增大到160MW時系統開始了功率振蕩。

圖8 時間常數為2ms時的直流傳輸容量圖

圖9是仿真在響應時間常數為4ms時的直流傳輸容量圖。在5s時把功率從100MW增加到260MW和276MW，由圖可知，當功率增大到260MW時系統仍然穩定，但是當功率增大到276MW時系統開始了功率振蕩。由此表明，當響應時間常數在大于9ms的某一范圍內時，時間常數的增加會導致系統直流傳輸容量增大。

圖9 時間常數為4ms時的直流傳輸容量圖

4．3 仿真結果和計算結果對比

由圖5可知，響應時間常數小于0．008s時，仿真結果與計算結果擬合度非常接近，誤差小于3%。當響應時間常數大于0．01s后，此時仿真模型的傳輸容量都是860MW，這是因為逆變站與交流電網的傳輸容量在850MW附近[17－18]的原因所導致。

5 結論

本文通過對雙端VSC－HVDC系統中的受端逆變站進行了直流側小信號阻抗建模，分析了直流系統的小擾動穩定條件，找到了逆變站的動態特性與直流傳輸容量之間的關系，并得出以下結論：

（1）VSC－HVDC系統的小信號穩定限制著直流傳輸容量。

（2）當響應時間常數很小時，可用恒功率負載來代替VSC－HVDC系統的逆變站。

（3）當響應速度很快，即負荷的恢復速度很快時，響應時間常數對VSC－HVDC系統的直流傳輸容量的約束力很小。