基于分布式溫度傳感的在線學習自適應模糊溫度預測法

李寧，尚雯珂

（西安交通大學電氣工程學院，陜西 西安 712046）

拉曼分布式光纖傳感器能夠沿光纖沿線測量溫度，基于拉曼散射的分布式光纖傳感器已成為被廣泛采用的可以監(jiān)測各種結(jié)構(gòu)溫度狀況的一種有前景的技術。但是，系統(tǒng)在火災等溫度突變事故中還無法快速有效實現(xiàn)對安全隱患的超前預警，系統(tǒng)的溫度響應時間受到了溫度傳遞滯后和單次解調(diào)過程的影響，只能在溫度異常時實施維護機制，若想要盡早發(fā)現(xiàn)問題，從源頭上對安全隱患采取預防措施，仍是一道技術難題。因此大量研究人員正致力于在不影響溫度預測精度的前提下提高預警時間的研究。

為了實現(xiàn)對火災等安全隱患的預測報警功能，研究人員提出了各種方案，例如：閾值預警方法[1]，溫差預警方法，可視化定位技術[2]，模糊溫差閾值法（FTDTM）[3]，離散系數(shù)預測溫度算法[4]，基于多階實時移動平均法的預警模型[1]等。在這些方法中，閾值預警和溫差預警的速度主要依賴于高速采集卡的采集速率和解調(diào)運行時間，對系統(tǒng)硬件要求較高[4]，不經(jīng)濟，無法做到安全準確和防患于未然。模糊溫差閾值法和離散系數(shù)預測溫度算法預測的準確性還有待提高。基于多階實時移動平均法的預警模型雖然預測溫度的平均絕對誤差達到了0．31℃，但在不同應用場景下需要建立不同的預警模型，使用時不方便，增加了工作量。因此在工業(yè)應用中，急需結(jié)構(gòu)簡單、成本較低、預測準確的超前預警系統(tǒng)。

本文提出了一種基于在線學習的自適應模糊溫度預測方法（Adaptive Fuzzy Temperature Prediction Method Based on Online Learning，AFTPM），該預警方法對系統(tǒng)硬件沒有特別要求，超前預警時間可以根據(jù)需求自由設定，測量準確度較高。該方法在模糊算法的基礎上通過設定適當?shù)恼撚驅(qū)崿F(xiàn)自適應，并不斷將實時數(shù)據(jù)存入歷史數(shù)據(jù)中進行在線學習，實時更新訓練數(shù)據(jù)，有效預測溫度趨勢。結(jié)果表明系統(tǒng)的平均預測溫度的絕對誤差為1．1℃，平均預測誤差百分率為3．06%，預測誤差的波動范圍約為±2．3℃。因此本文對預防火災的應用具有一定的理論指導作用。

1 原理

為了優(yōu)化拉曼分布式光纖傳感系統(tǒng)在實際應用中針對火災等環(huán)境溫度突變的反應速度，提高系統(tǒng)預警響應時間，實現(xiàn)超前預警，本文提出了基于在線學習的自適應模糊溫度預測法。常用的預警方法是通過自定義固定閾值溫度Th和計算溫差閾值Td來實現(xiàn)報警功能，但是在實際遠距離檢測中，希望在火災安全隱患發(fā)生之前能夠超前預警，而傳統(tǒng)的方法只能在溫度異常時實施維護機制，并不能保證從源頭解除隱患，因此面向火災安全監(jiān)控領域進行超前預警報警的難題亟待解決。

為了打破系統(tǒng)因傳感光纜溫度傳遞滯后效應帶來溫度響應時間的限制，參考了文獻[3，5－10]的模糊算法，本文提出了一種基于在線學習的自適應模糊溫度超前預測法。這是一種可以提前準確預測溫度趨勢的有效預警方法，在模糊算法的基礎上通過設定適當?shù)恼撚驅(qū)崿F(xiàn)自適應，并不斷將實時數(shù)據(jù)疊加到歷史數(shù)據(jù)中進行在線學習，實時更新訓練數(shù)據(jù)，能夠有效預測溫度趨勢。

RDTS（Raman Distributed Temperature Sensor，RDTS）實驗裝置框圖如圖1所示。該系統(tǒng)硬件設備包括高速脈沖激光調(diào)制器（中心波長1550nm），波分復用器（波長1450nm、1550nm、1660nm），多模光纖（芯徑62．5／125μm），雪崩光電二極管（帶寬100MHz），高速數(shù)據(jù)采集卡（采樣頻率100MSa／S）。

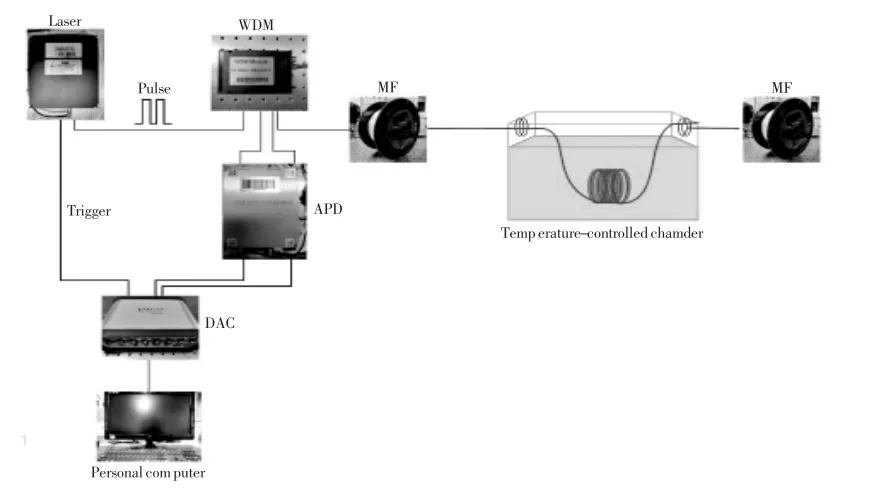
圖1 RDTS實驗裝置框圖

當RDTS系統(tǒng)運行時，該系統(tǒng)由光發(fā)射模塊輸出一個10ns的光脈沖，其采用溫度控制，光學性能穩(wěn)定。光信號進入波分復用器后耦合到被測光纖，產(chǎn)生后向斯托克斯光信號和反斯托克斯光信號，后向散射光通過1660nm和1450nm兩個通道分成兩路分別進入光電探測器進行光電轉(zhuǎn)換和放大，最后通過采集卡采集信號，并由上位機讀取兩路數(shù)據(jù)解調(diào)出溫度。

1．1 溫度解調(diào)原理

當中心波長為1550nm的光脈沖入射到被測光纖時，光纖中的脈沖光和光學聲子由于非彈性碰撞發(fā)生能量轉(zhuǎn)移，產(chǎn)生自發(fā)拉曼散射（Spontaneous Raman Scattering，SpRS）。由于激光脈沖和晶格振動模式的相互作用，處于低能級的光纖分子吸收入射光子能量，進入虛能級狀態(tài)。由于光纖分子在虛能級狀態(tài)極其不穩(wěn)定，會從虛能級狀態(tài)向高能級躍遷，過程中會釋放一個光學聲子，同時產(chǎn)生一個低頻的光子，即斯托克斯光子。而處在虛能級狀態(tài)的光纖分子也會向低能級躍遷，過程中會吸收一個聲子，同時釋放出一個高頻的光子，即反斯托克斯光子。因為晶格振動受環(huán)境溫度的影響[1]，SpRS的強度對光纖溫度敏感。通常選擇對溫度敏感的反斯托克斯光作為傳感信號，而選擇對溫度不敏感的斯托克斯光作為參考信號，這樣能消除光纖在受到除溫度外的其他因素干擾時引起的溫度測量誤差的影響。

溫度T下的反斯托克斯光強與斯托克斯光強之比的表達式Fas－s（T）為：

其中：Ra（T）和Rs（T）為反斯托克斯光和斯托克斯光的溫度調(diào)制函數(shù)；Ua（T）和Us（T）為反斯托克斯光和斯托克斯光的輸出電壓；Qa和Qs為光電響應系數(shù)；Ka和Ks為反斯托克斯光和斯托克斯光的散射系數(shù)；va和vs為反斯托克斯光和斯托克斯光的頻率；aa和as為反斯托克斯光和斯托克斯光在光纖中的傳播損耗；L為傳播距離。

反斯托克斯光和斯托克斯光的溫度調(diào)制函數(shù)之比的表達式為：

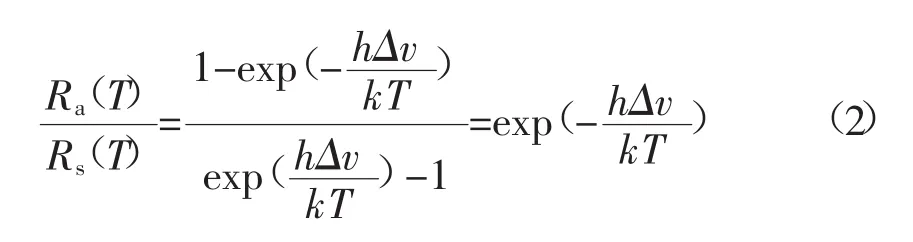
式中：h代表普朗克常數(shù)，h＝6．626×10－34J·S；k代表波爾茲曼常數(shù)，k＝1．380×10－23J·K－1；Δv代表拉曼頻移量，Δv＝1．32×1013Hz；T是開爾文（Kelvin）絕對溫度。比較溫度T和T0下的光強比Fas－s（T）和Fas－s（T0），我們可以得到溫度T的表達式為：

1．2 自適應模糊溫度預測原理

自適應模糊溫度預測法（AFTPM）認為，從t時刻到t＋1時刻的溫度變化與t時刻與過去時刻之間的溫度變化相關。在t＋1時刻的溫度與t時刻的溫度相關性最高。如果在過去的幾個時刻里溫度趨勢在上升，我們認為下一時刻溫度會升高。如果過去幾個時刻里氣溫呈下降趨勢，我們認為下一時刻溫度會降低。我們使用溫度在t時刻作為預測基準，利用t－1時刻及之前的歷史溫度進行訓練，來預測t＋1時刻的溫度。在預測t＋2時刻的溫度時，將t時刻的溫度也加入歷史數(shù)據(jù)，并對預測規(guī)則進行更新。基于在線學習的AFTPM包括以下八個步驟：

（1）論域的確定

根據(jù)歷史時刻溫度的最大值Tmax和最小值Tmin設置論域U，如式（2）所示，其中D1和D2根據(jù)預測精度由自己定義，用于調(diào)節(jié)論域的范圍。

（2）模糊集的劃分

針對論域等間隔劃分成n份，得到u1，u2…un，n由自己給定，該數(shù)量與后續(xù)設定的模糊集的數(shù)量相同。

（3）確定模糊集和隸屬函數(shù)

模糊集可以描述為：

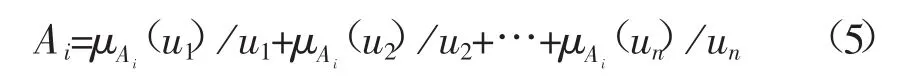
其中，μAi是模糊集Ai的隸屬度函數(shù)，這里選用三角隸屬函數(shù)，μAi（uj）表示uj在Ai中的隸屬度。

假設n＝3，變量溫度用模糊集可以表示為A1＝溫度低，A2＝溫度適中，A3＝溫度高。

（4）對歷史數(shù)據(jù)進行模糊化

對每一個歷史溫度進行模糊化，確定其隸屬的模糊集Ai：

（5）根據(jù)歷史經(jīng)驗設計模糊規(guī)則Ai→Aj

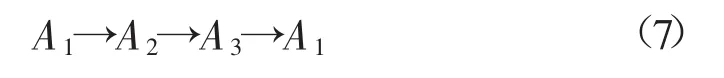
（6）根據(jù)模糊規(guī)則求解模糊關系矩陣R

模糊規(guī)則如表1所示：

表1 模糊規(guī)則對應表

模糊關系矩陣為：

（7）預測

先對當前時刻的值進行模糊化，并根據(jù)當前時刻溫度的模糊值，預測下一時刻溫度的模糊值，再對Apre進行解模糊。

（8）解模糊

我們只信任預測模糊值的最大值。如果最大值只有一個，那么就取對應模糊集的中點，然后再乘以最大值的數(shù)值。如果有k個，對應模糊集中點相加除以k。基于在線學習的AFTPM流程圖如圖2所示。

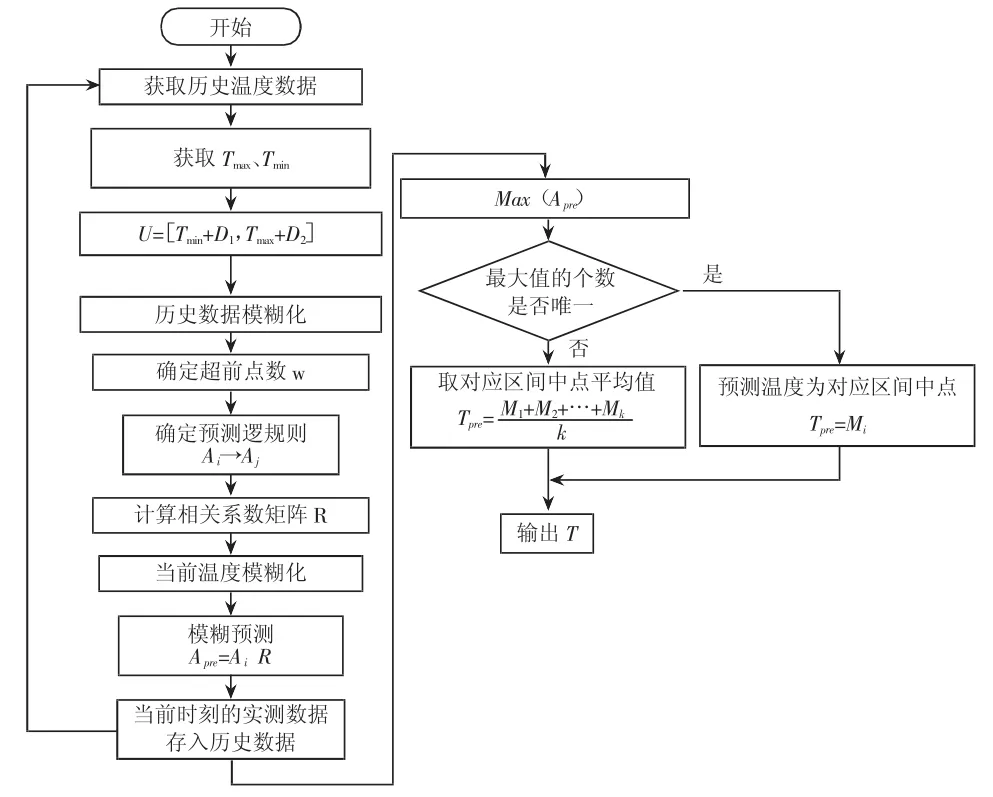
圖2 基于在線學習的AFTPM流程圖

2 實驗結(jié)果

如圖3所示為被測光纖第638m位置處實時測量溫度和預測溫度曲線圖。在圖3中，藍色曲線表示實際測得的溫度，紅色曲線表示預測的溫度，溫度值都是經(jīng)過自適應閾值小波包去噪的結(jié)果[11－12]，可以看出，藍線和紅色基本重合，預測結(jié)果比較準確。圖3（b）顯示了預測溫度與實際測量溫度之間的測量誤差，結(jié)果表明連續(xù)測量230分鐘內(nèi)平均預測溫度的絕對誤差為1．25℃，平均預測誤差百分率為3．6%，預測誤差的波動范圍約為±3．5℃。根據(jù)測溫結(jié)果，AFTPM預警模型可以很好地測量實際溫度并預測下一時刻的溫度趨勢，系統(tǒng)參數(shù)符合很多工程例如井下測溫預警等要求。若想進一步提高預測精度，減少誤差，我們可以通過增加系統(tǒng)檢測頻率來實現(xiàn)。

圖3 被測光纖第638m位置處實時測量溫度和預測溫度曲線圖

圖4為不同超前點數(shù)w對預測精度影響的結(jié)果圖，展示了在不同w的下的實際溫度信號和預測溫度信號的差異。如果RDTS系統(tǒng)以一分鐘的時間間隔收集光纖沿線的溫度信息，若w取1，則AFTPM可以預測從當前溫度開始一分鐘后相同位置處的溫度；若w取2，可以預測兩分鐘后相同位置處的溫度；若w取n，則可以預測n分鐘后相同位置處的溫度。因此，若想要提高超前預警時間，可以通過增大超前點數(shù)w的值來實現(xiàn)。從圖4（a）中可以看出，當w的值較小時，實際溫度信號和預測溫度信號幾乎沿同一趨勢變化，二者之間的溫度差值也很小，這意味著信號的重合性很好，測量精度較高。隨著w值的增加，當w取8時，預測溫度出現(xiàn)明顯振蕩，表明測量精度下降了，實驗結(jié)果如圖4（d）所示。這說明w的值并不是越大越好，w的值越大，超前預警時間更長，但測量誤差也會隨之增大，使用時應根據(jù)實際應用場景來選取w的值。

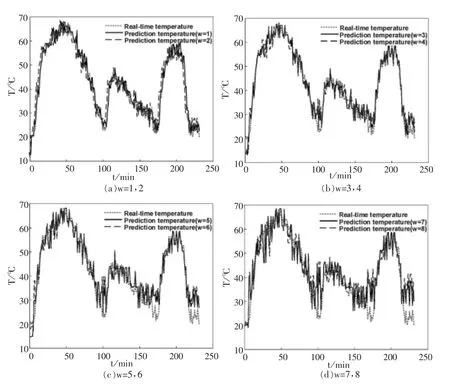
圖4 不同超前點數(shù)w下的實際溫度與預測溫度圖

從圖4的結(jié)果還可以看出，在100分鐘、175分鐘以及215分鐘的時候，預測的溫度誤差比較明顯，造成這種現(xiàn)象的原因是實際溫度值發(fā)生了較大的變化。

為了提高在溫度變化較大時的預測精度，本文提出了基于在線學習的AFTPM，其實驗結(jié)果如圖5所示。將實時測量的溫度數(shù)據(jù)存入歷史數(shù)據(jù)中，不斷更新訓練數(shù)據(jù)庫，使其能實時捕捉到溫度變化信息，從而預測得到更加準確的溫度數(shù)值。圖5（a）顯示了未采用在線學習的預測結(jié)果，圖5（c）展示了未采用在線學習的誤差結(jié)果，可以明顯看出，三個溫度變化較大的位置誤差越來越大。而采用了在線學習之后，誤差基本趨于穩(wěn)定，不會出現(xiàn)較大波動，預測的精度也顯著提高，如圖5（b）、5（d）所示。結(jié)果表明平均預測溫度的絕對誤差從1．6℃降到1．1℃，平均預測誤差百分率從4．31%降到3．06%，最大誤差值從6．9℃降到2．6℃，預測誤差的波動范圍降到約為±2．6℃。

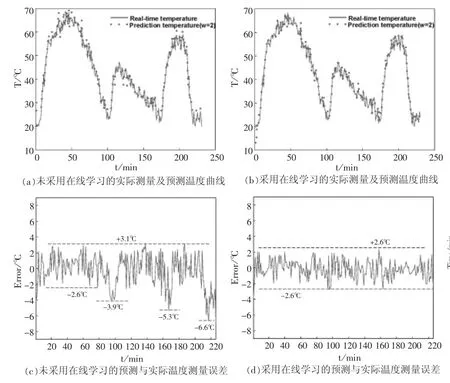
圖5 基于在線學習的AFTPM溫度曲線圖

以上針對的是單點測量，在實際應用中，我們可以根據(jù)需求預測任何位置的溫度值，即分布式預測。圖6為2D溫度顏色圖，圖上顯示了光纖沿線不同位置的溫度變化，以及光纖同一位置處不同時間的溫度變化。從圖中可以看出，550m到750m這一段光纖溫度隨時間發(fā)生明顯變化，展示了溫度從常溫升到67℃，隨之慢慢降溫到24℃，再升溫到45℃，降到室溫之后繼續(xù)加熱到58．5℃，最后降到室溫的過程，而未進行溫度控制的光纖一直處于常溫狀態(tài)。實驗中總共測量232組數(shù)據(jù)，取前160組數(shù)據(jù)作為歷史數(shù)據(jù)，對剩下的測量數(shù)據(jù)進行溫度預測。圖7為實際和預測溫度顏色圖，其中（a）為2D實際溫度顏色圖，（b）為2D預測溫度顏色圖。對比兩圖，可以看出預測溫度值和真實溫度值是完全相同的，說明基于在線學習的AFTPM能夠準確預測拉曼分布式光纖溫度。

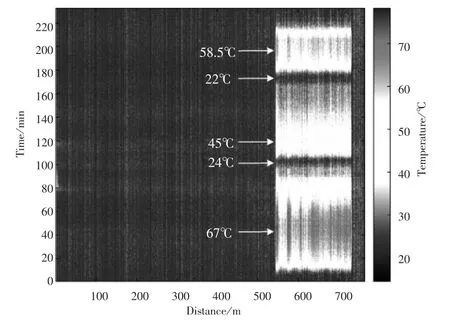
圖6 2D溫度顏色圖

圖7 實際和預測溫度顏色圖

3 結(jié)論

本文提出并通過實驗證明了基于RDTS系統(tǒng)面向火災預警的基于在線學習的AFTPM。AFTPM通過分析RDTS系統(tǒng)的溫度數(shù)據(jù)，不僅能快速響應實時溫度，還能超前預測未來溫度。系統(tǒng)警告時間取決于系統(tǒng)單次解調(diào)時間和超前點數(shù)的選擇。當系統(tǒng)設置超前點數(shù)為2時，平均預測溫度的絕對誤差為1．1℃，平均預測誤差百分率為3．06%，預測誤差的波動范圍約為±2．6℃。

本文通過分析超前點數(shù)的大小與超強預警時間和預測精度的關系來選取合適的w值，從而在保證預測精度的同時提高預警時間。為了保證溫度變化較大時的預測精度，控制預測誤差在小范圍內(nèi)波動，在原本的AFTPM基礎上加入在線學習過程，通過分析在線學習算法使用前后的預測誤差，從而證明該算法的加入能夠有效降低預測誤差，尤其是在溫度變化較大的位置。我們還對被測光纖沿線上每個位置進行了分布式預測，得到的預測溫度基本吻合。

針對高精度應用場景，本文所采用的基于在線學習的AFTPM對預測精度仍有改進的潛力，我們需與時俱進，不斷改進。